Цилиндр. Площадь поверхности цилиндра

1. Урок геометрии в 11 классе

По теме:
«Цилиндр. Площадь
поверхности цилиндра».

2. Цилиндр. Площадь поверхности цилиндра.

3. Цели урока:

• Образовательные:
ввести понятие цилиндра;
формирование понятия площади полной и боковой поверхности
цилиндра;
вывести формулы площадей поверхностей цилиндра и
сформировать умения применять их при решении задач;
проверить уровень первичного усвоения материала учащегося;
• Развивающие:
развитие пространственного мышления, культуры математической
речи,
развитие коммуникативных умений: умение слушать и слышать,
правильно задавать вопросы;
• Воспитательные:
воспитание ответственного отношения к учебному труду.

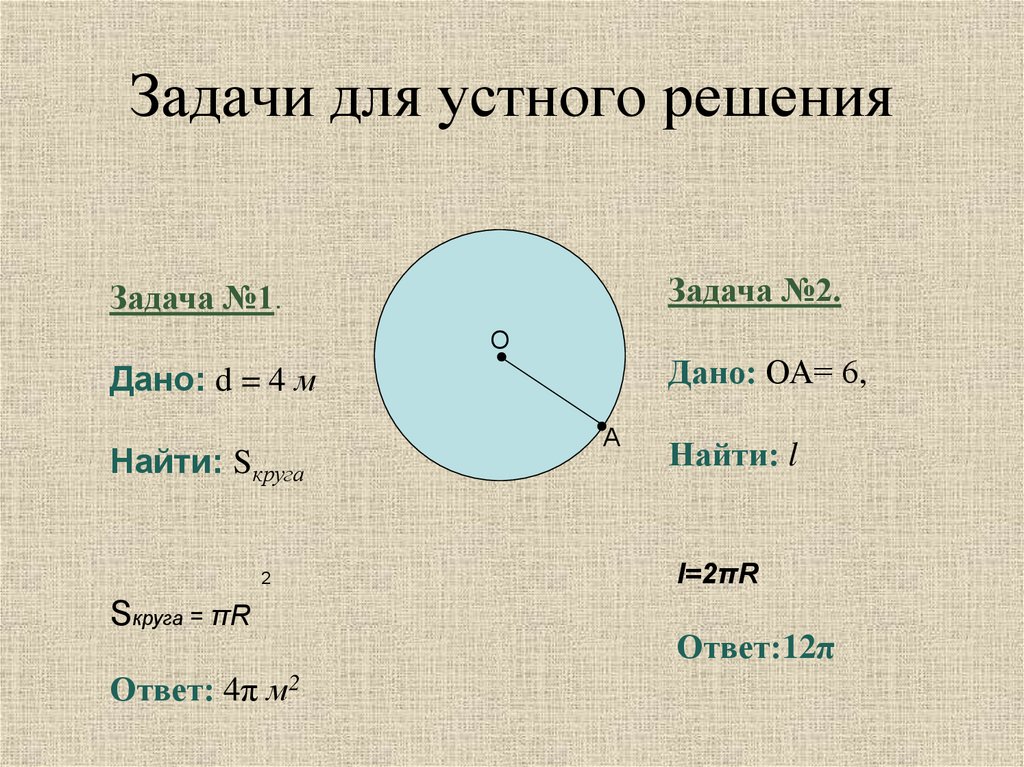
4. Задачи для устного решения

Задача №2.
Задача №1.
О
Дано: ОА= 6,
Дано: d = 4 м
Найти: Sкруга
2
Sкруга = πR
Ответ: 4π м2
A
Найти: l
l=2πR
Ответ:12π

5.

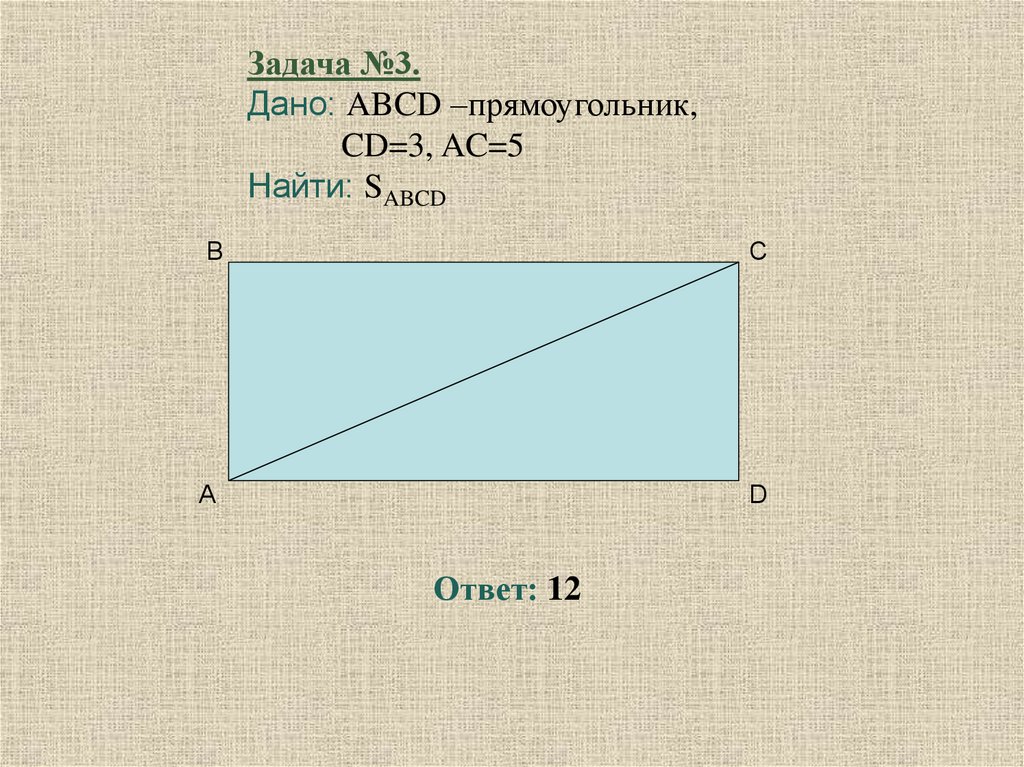
Задача №3.
Дано: ABCD –прямоугольник,
CD=3, AC=5
Найти: SABCD
B
C
A
D
Ответ: 12

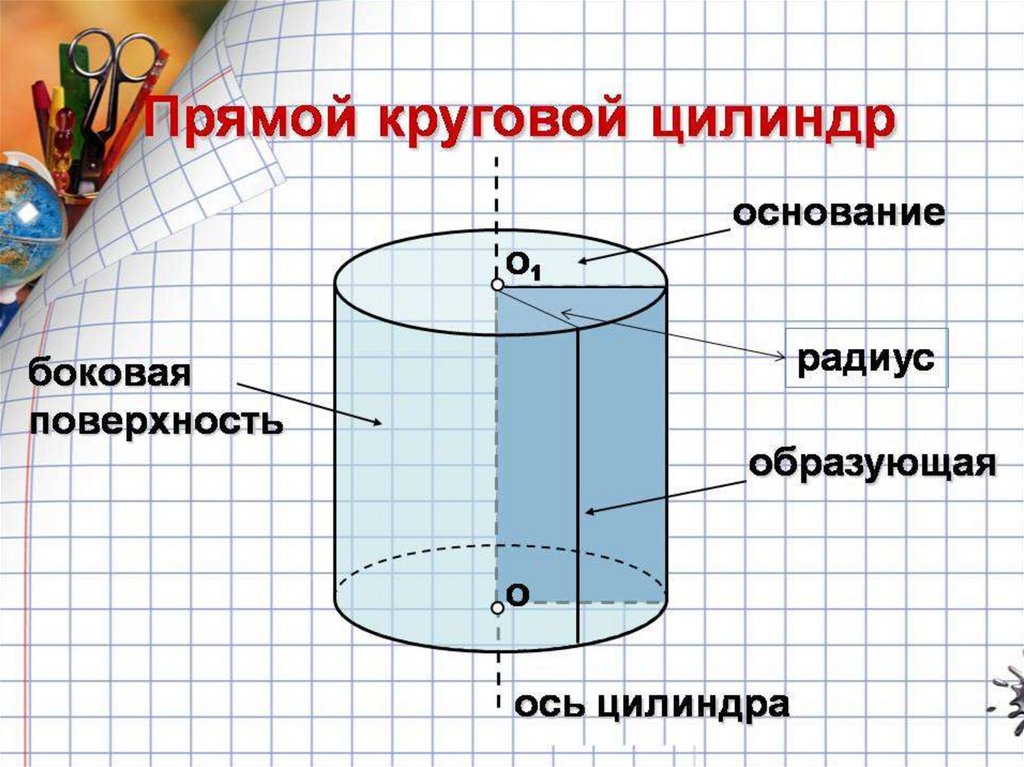
6. ЦИЛИНДР.

O
B
A
O1

7.

8.

9. Площадь поверхности цилиндра

O
B1
B
B
h
O1
A
A
2πR
Sцилиндра = 2Sосн+Sбок
Sосн = πR2
Sбок = 2πRh
Sцилиндра= 2πR(R+h)
A1

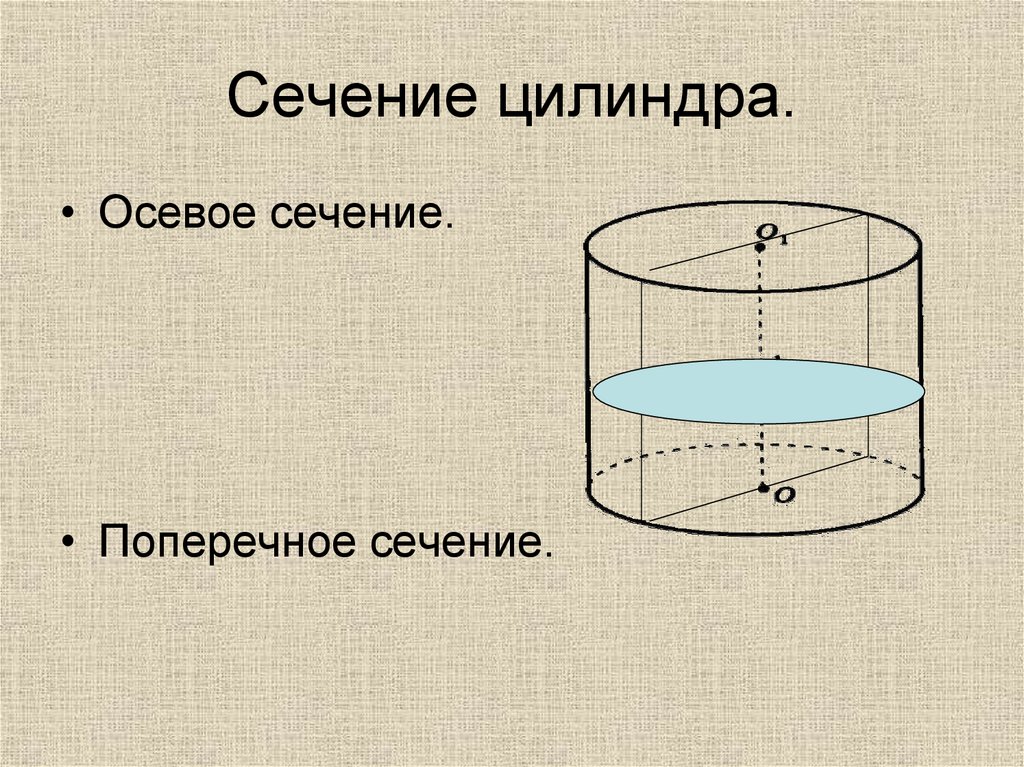
10. Сечение цилиндра.

• Осевое сечение.
• Поперечное сечение.

11.

№523
Осевое сечение цилиндра – квадрат,
диагональ которого равна 20 см. Найдите:
а) высоту цилиндра; б) So цилиндра
Решение.
B
C
1. Проведем диагональ АС
сечения АВСD.
2. ADC – равнобедренный,
прямоугольный, АD=DC, h = 2r,
45
20
CAD = ACD=45 , тогда
2
h AC cos 45 20
10 2 .
2
3. Найдем радиус основания
45
A
D
4. Найдем площадь основания
Ответ: а )10 2 ;
б )50 .
h 10 2
r
5 2.
2
2
2
So r 5 2 50 .
2

12.

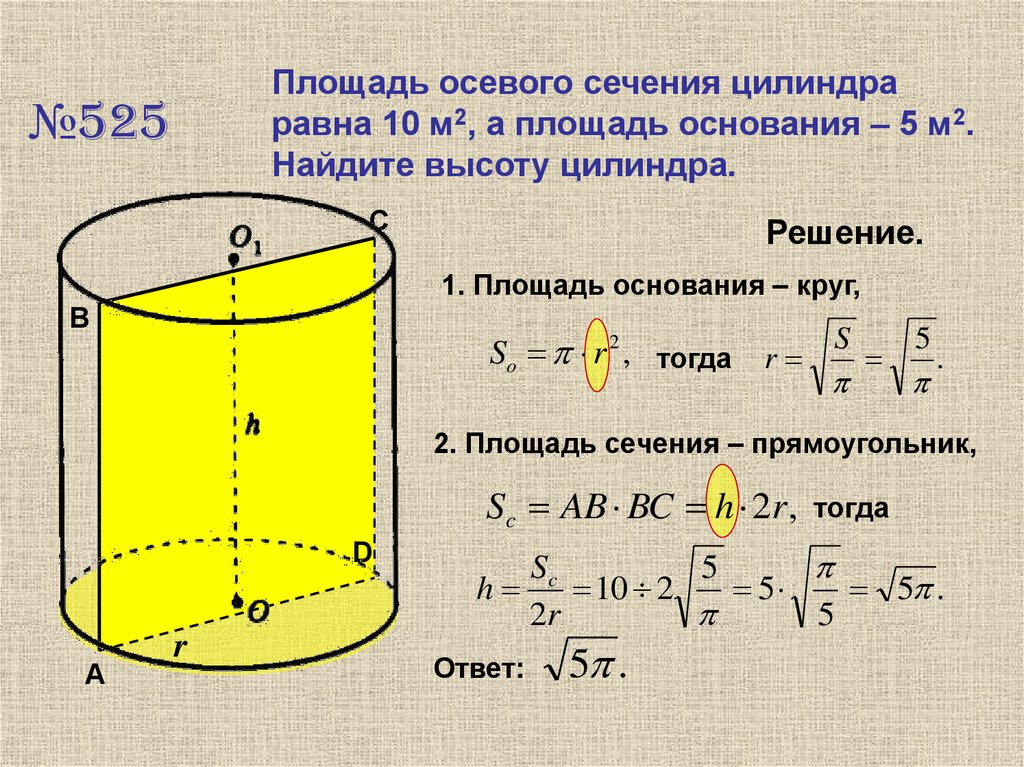
Площадь осевого сечения цилиндра
равна 10 м2, а площадь основания – 5 м2.
Найдите высоту цилиндра.
№525
C
Решение.
1. Площадь основания – круг,
B
So r 2 , тогда r S 5 .
2. Площадь сечения – прямоугольник,
Sc AB BC h 2r ,
D
A
r
тогда
Sc
5
h
10 2
5
5 .
2r
5
Ответ:
5 .

13.

№527
В
Концы отрезка АВ лежат на разных основаниях цилиндра.
Радиус цилиндра равен r, его высота – h, расстояние между
прямой АВ и осью цилиндра равно d. Найдите: a) высоту,
если r = 10, d = 8, AB = 13.
1. Построим отрезок АВ.
Решение.
2. Проведем радиус АО.
3. Построим отрезок d.
4. Отрезок ОК – искомое расстояние.
5. Из прямоугольного АОК находим:
a
AK r 2 d 2 100 64 6,
С
К
А
значит АС = 12.
6. Из прямоугольного АВС находим:
d r
ВС АВ 2 АС 2 169 144 5.
r
Итак, h = 5.
Ответ: 5.

14. Постановка домашнего задания

• Прочитать п. 59, 60. Выучить формулы
площадей поверхностей тел вращения.
• № 522, 524, 526.