Similar presentations:
Вписанная окружность
1. Вписанная окружность
Учитель математики ГБОУ гимназии № 1504 Железнова Я.А.2. Определение
Если все стороны многоугольникакасаются окружности, то
окружность называется вписанной
в многоугольник,
а многоугольник – описанным около
этой окружности.
3.
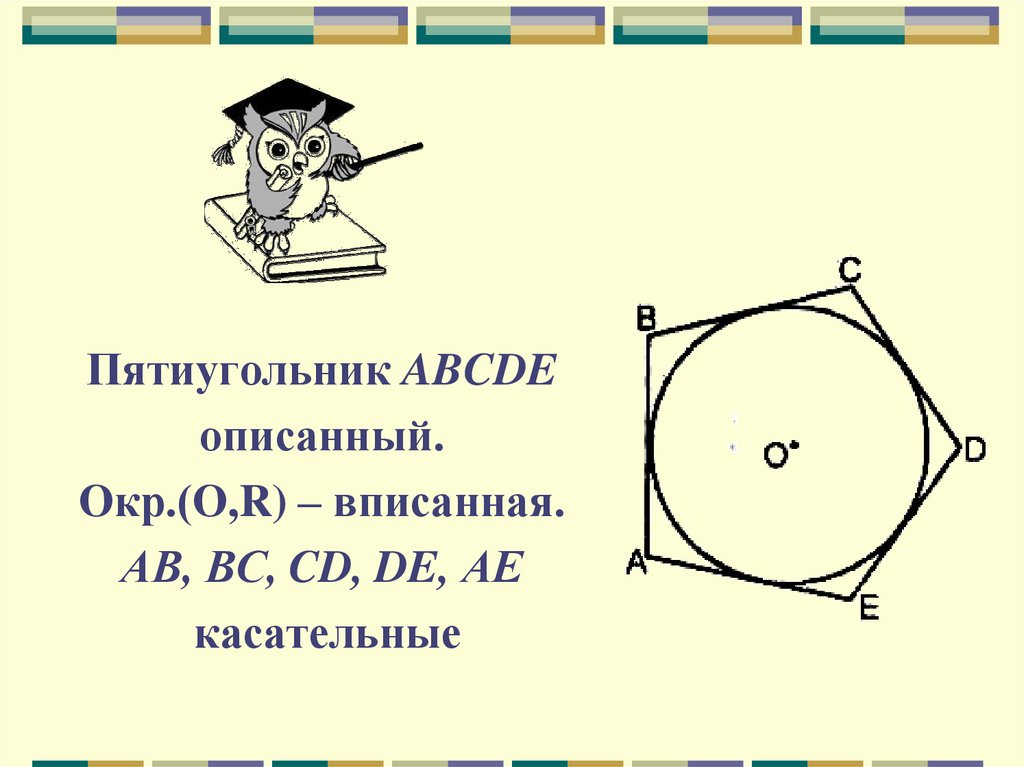
Пятиугольник ABCDEописанный.
Окр.(О,R) – вписанная.
АВ, ВС, CD, DE, АЕ
касательные
4.
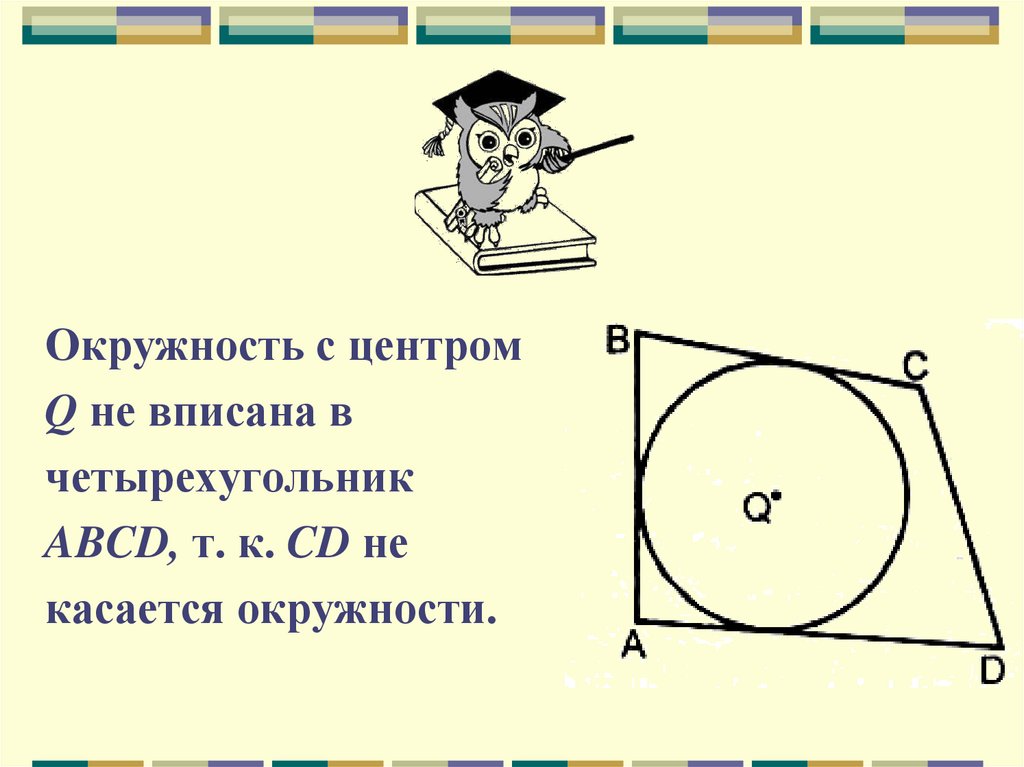
Окружность с центромQ не вписана в
четырехугольник
ABCD, т. к. CD не
касается окружности.
5. ТЕОРЕМА
В любой треугольник можновписать окружность.
Замечание: в треугольник можно
вписать только одну окружность.
6. Дано
АABC
AA1 , BB1 , CC1 биссектрисы
AA1 BB1 CC1 O
Доказать, что
окр. (О; R)вписанная.
О
С
В
7. Доказательство
ПроведемДоказательство
OK AB, OM AC, OL BC
Т.к. точка О лежит на биссектрисах,
то она равноудалена от АВ, ВС, АС,
т.е. OK OL OM
Значит точки K , L, M окр (O; OK )
Т.к. OK AB, OM AC, OL BC K
то AB, AC,CB – касательные.
Значит окр.(О; ОR) вписанная.
В
А
M
О
С
L
8. Важный вывод 1
Центр вписанной втреугольник окружности
лежит в точке пересечения
его биссектрис и
равноудален от его сторон.
9. Важный вывод 2
Радиус окружностивписанной в треугольник
равен расстоянию от центра
окружности до сторон
треугольника.
10.
Не во всякий четырехугольникможно вписать окружность.
Если же в четырехугольник
можно вписать окружность, то
его стороны обладают
следующим свойством:
11. Свойство
В любом описанномчетырехугольнике
суммы противоположных
сторон равны.
12.
АВСDописанный
четырехугольник.
В
А
O
С
AB+CD=BC+AD
D
13.
окружностис
a + b + c +d
CD
AD
доказать
d
14. Верно и обратное утверждение
Если суммы противоположных сторонвыпуклого четырехугольника равны,
то в него можно вписать окружность.
Это признак описанного
четырехугольника.
15. Свойство описанного многоугольника
Площадь описанногомногоугольника равна половине
произведения его периметра на
радиус вписанной окружности.
S ABCD... K PABCD... K r
1
2
16.
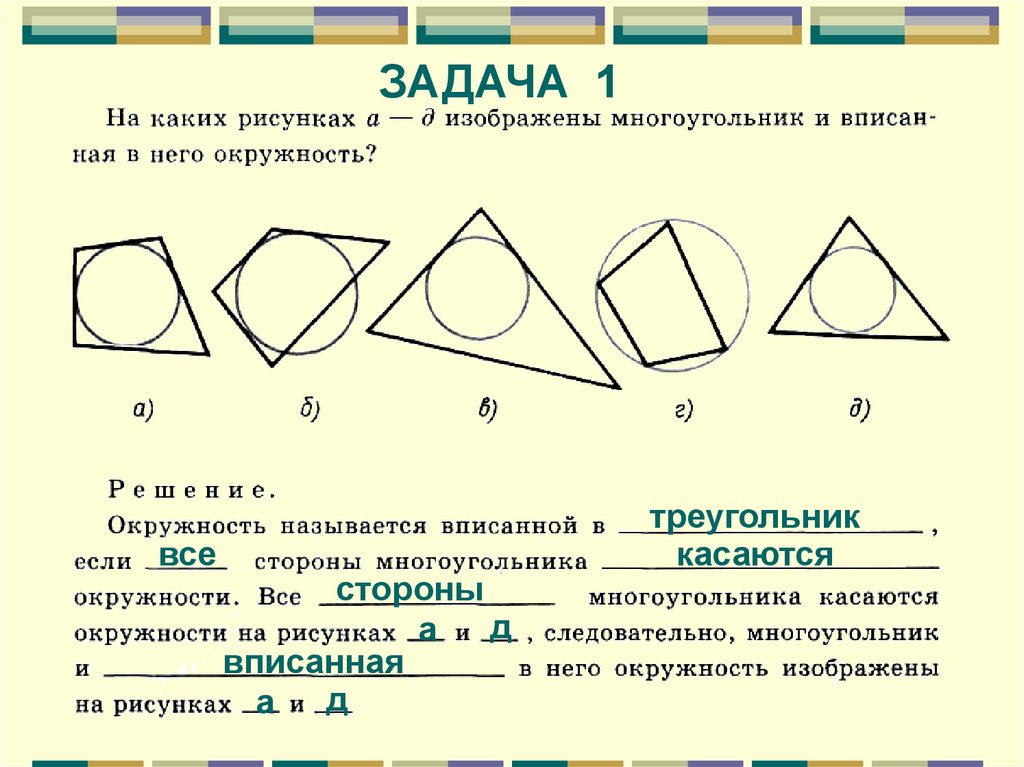
ЗАДАЧА 1все
стороны
д
а
вписанная
а д
треугольник
касаются
17. Задача 2
ОКРУЖНОСТИТОЧКИ
3
BT
6
HB+BT+AT
2
3+6
28
АМ
MC+СH
СH
18.
ЗАДАЧА 3КАСАНИЯ
АС
ВЫСОТА
ТРЕУГОЛЬНИКА
АОВ
ВЫСОТА
ОЕ
ОМ
АС·OH
1
2
1
2
ОH
ОМ
S AOC
AC· r
r
60·4
120
1
2
BС
19. № 690
Дано:В
ABC равнобедренный
АС-основание
окр (О; R) вписанная
AB = 60,
BD – высота,
ВО : OD = 12 : 5,
Найти АС
K
O
А
D
С
20. № 691
Дано: ABC равнобедренныйАС-основание
В
окр (О; R) вписанная
Точки K, N, D –точки
касания.
ВК : КА = 4 : 3
Найти P
ABC
N
K
O
А
D
С
21. № 693 (a)
ВДано: ABC прямоуголь ный
C 90
окр (О;4) вписанная
АВ = 26
М, N, K – точки касания
Найти PABC
N
O
М
С
K
A
22. № 698
Кратко!23. Подведем итог :
Какая окружность называется вписанной вмногоугольник?
Какой многоугольник называется описанным
возле окружности?
В любой ли треугольник можно вписать
окружность?
Сколько окружностей можно вписать в
треугольник?
Где лежит центр вписанной окружности?
24. Подведем итог :
Чему равен радиус окружности,вписанной в треугольник?
В любой ли четырехугольник можно
вписать окружность?
Сформулируйте свойство
описанного четырехугольника
Сформулируйте признак описанного
четырехугольника
25. Домашние задание
П.74. читать,Теория из тетрадки, формулировки
знать наизусть.
№ 689, 692, 693 (б), 695






















 mathematics
mathematics








