Вписанная окружность. 8 класс

1.

16 апреля
Классная работа
Тема: Вписанная окружность.

2. Цели урока:

1.Познакомится с определением
вписанной окружности.
2.Изучить доказательство теоремы о
вписанной окружности.
3.Решение задач по данной теме.

3.

K
E
D
F
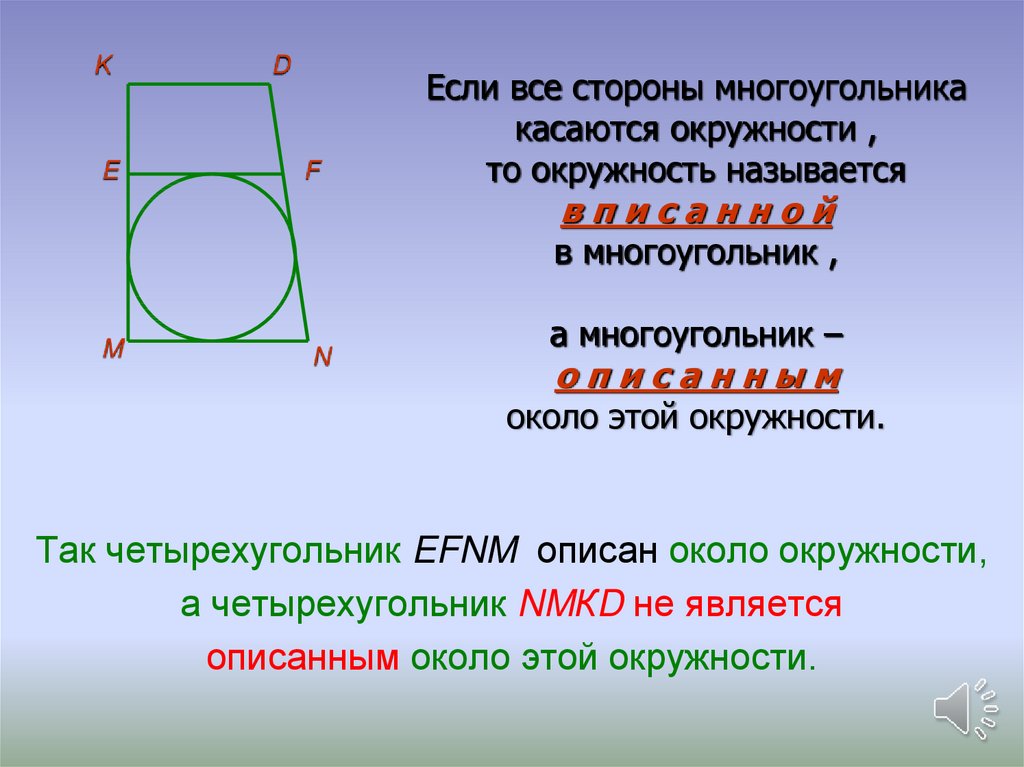
Если все стороны многоугольника
касаются окружности ,
то окружность называется
вписанной
в многоугольник ,
M
N
а многоугольник –
описанным
около этой окружности.
Так четырехугольник EFNM описан около окружности,
а четырехугольник NMКD не является
описанным около этой окружности.

4. В любой треугольник можно вписать окружность.

Теорема
В любой треугольник можно
вписать окружность.

5.

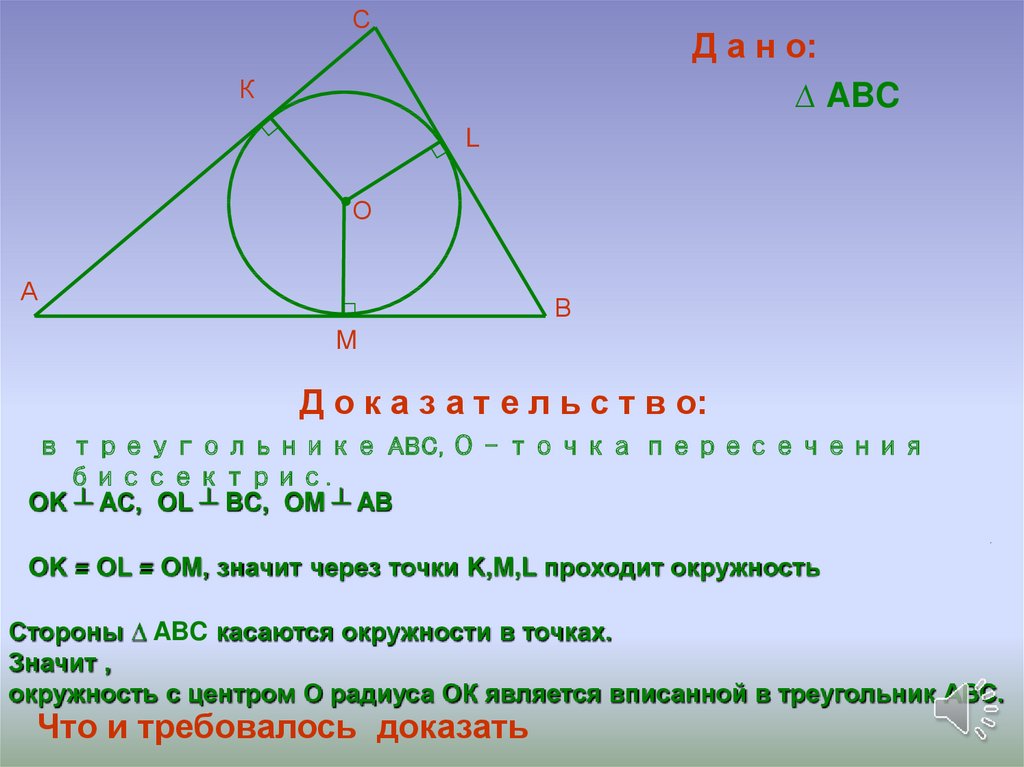
С
Д а н о:
∆ ABC
К
L
О
А
В
M
Д о к а з а т е л ь с т в о:
в треугольнике ABC, О – точка пересечения
биссектрис.
OK ┴ AС, OL ┴ BC, OM ┴ AB
OK = OL = OM, значит через точки K,M,L проходит окружность
Стороны ∆ ABC касаются окружности в точках.
Значит ,
окружность с центром О радиуса ОК является вписанной в треугольник АВС.
Что и требовалось доказать

6.

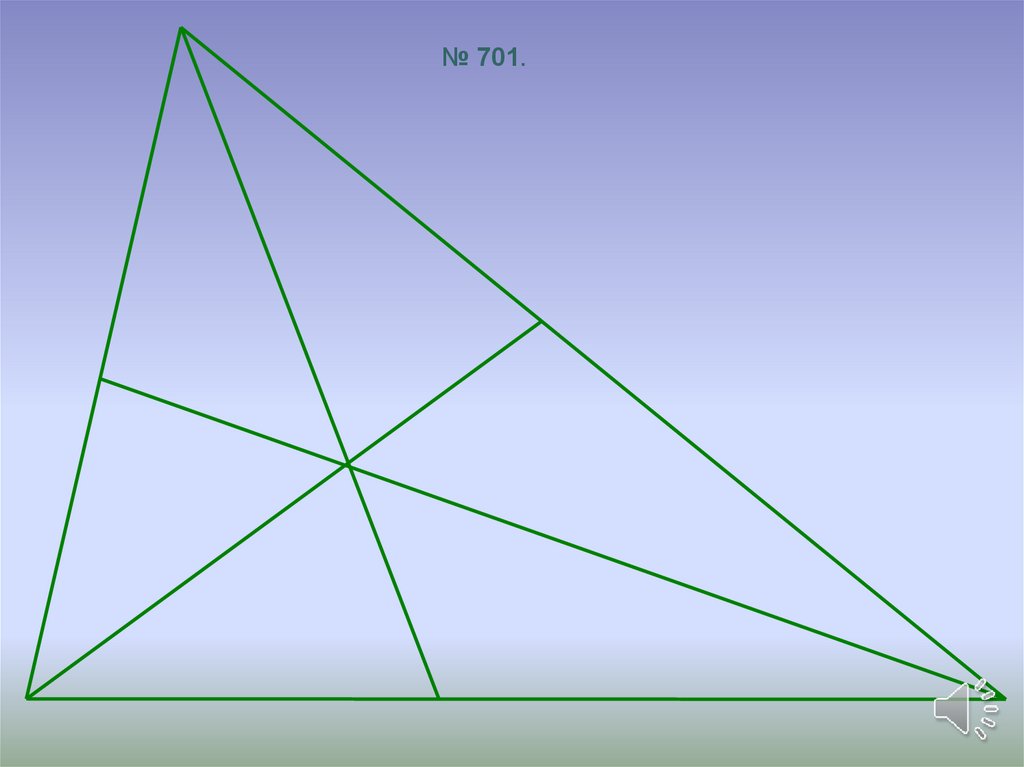
№ 701.

7. Домашняя работа :

П. 77 выучить теорему, № 689
Вопросы для повторения:
1. Что называется вписанной окружностью?
2. Что является центром вписанной окружности?
3. В любой ли треугольник можно вписать окружность?