Вписанная в треугольник окружность

1. Вписанная окружность

2. Вписанная окружность

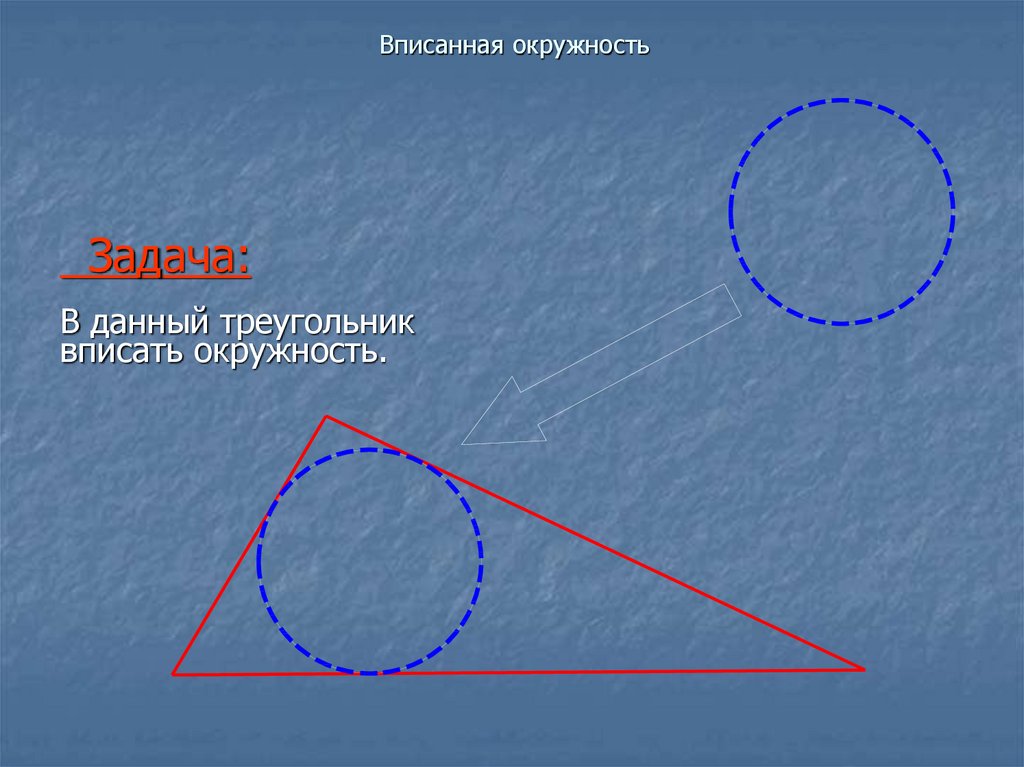
Задача:
В данный треугольник
вписать окружность.

3. Вписанная окружность

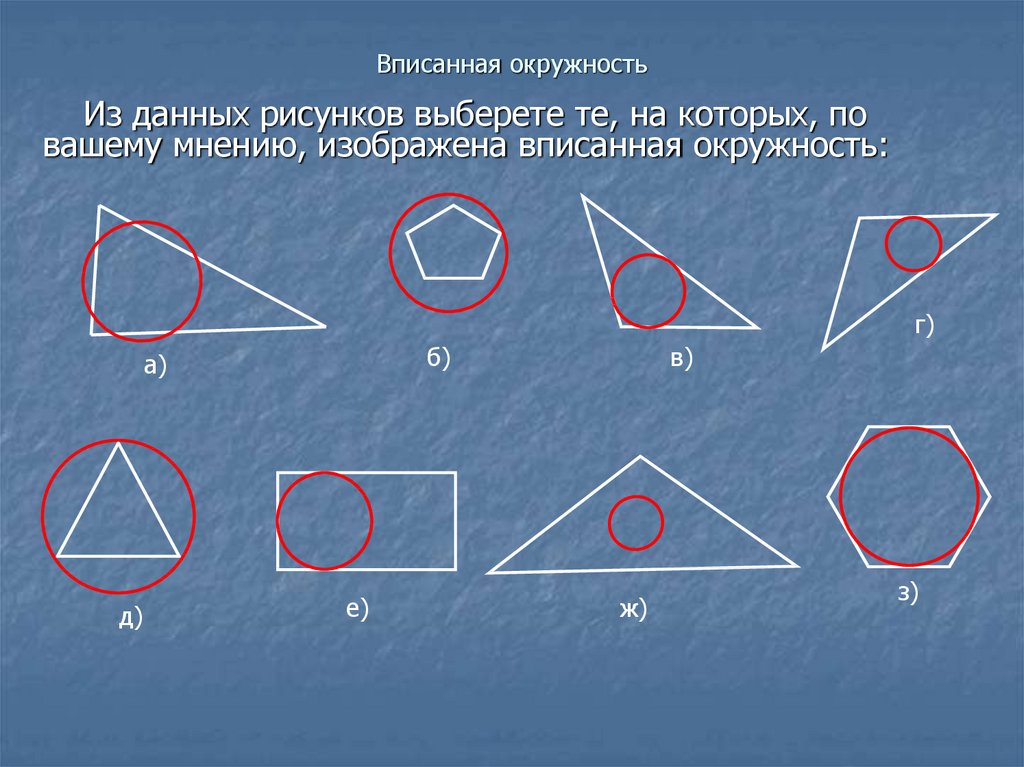
Из данных рисунков выберете те, на которых, по
вашему мнению, изображена вписанная окружность:
г)
б)
а)
д)
е)
в)
ж)
з)

4. Вписанная окружность

Определение:
Окружность называется вписанной в
многоугольник, если она касается всех
его сторон.

5. Вписанная окружность

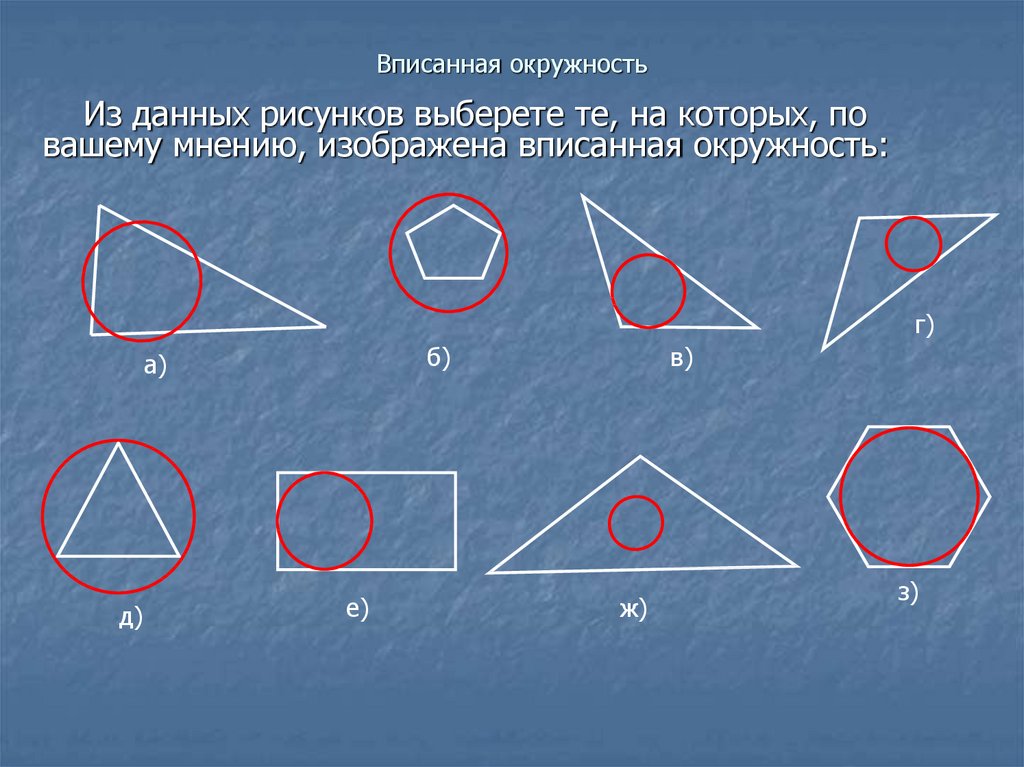
Из данных рисунков выберете те, на которых, по
вашему мнению, изображена вписанная окружность:
г)
б)
а)
д)
е)
в)
ж)
з)

6. Вписанная окружность

Как вписать окружность в треугольник?
В
Центр?
Радиус?
А
С

7. Вписанная окружность

Предположим, что вписали окружность.
В
О
А
С

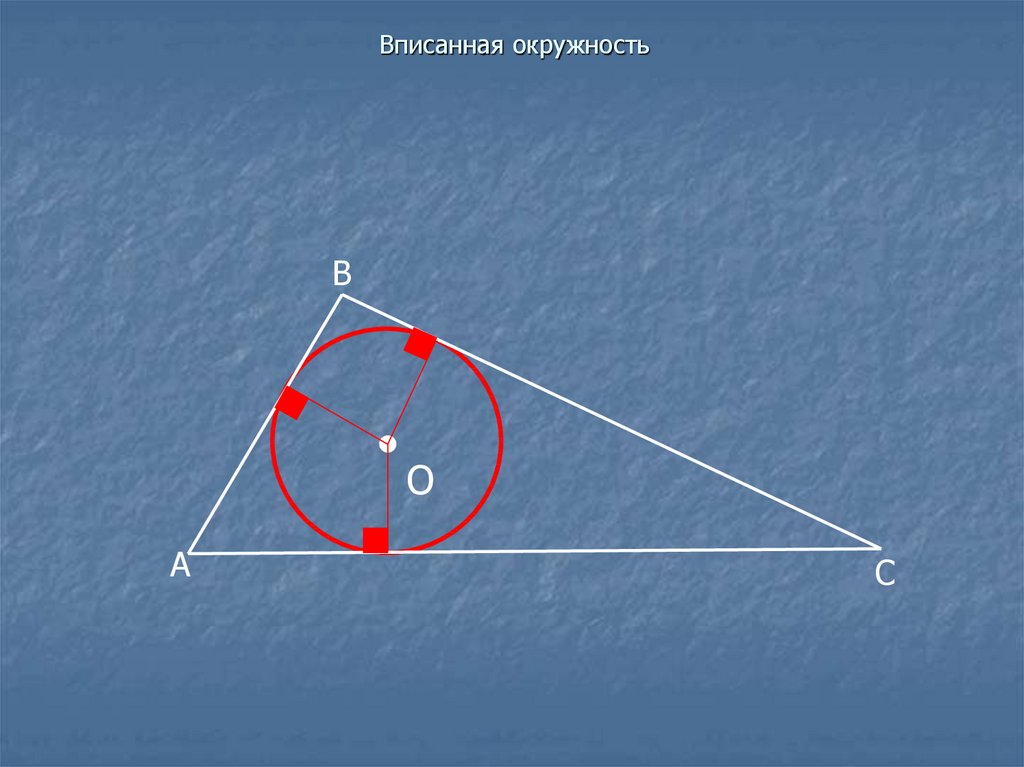
8. Вписанная окружность

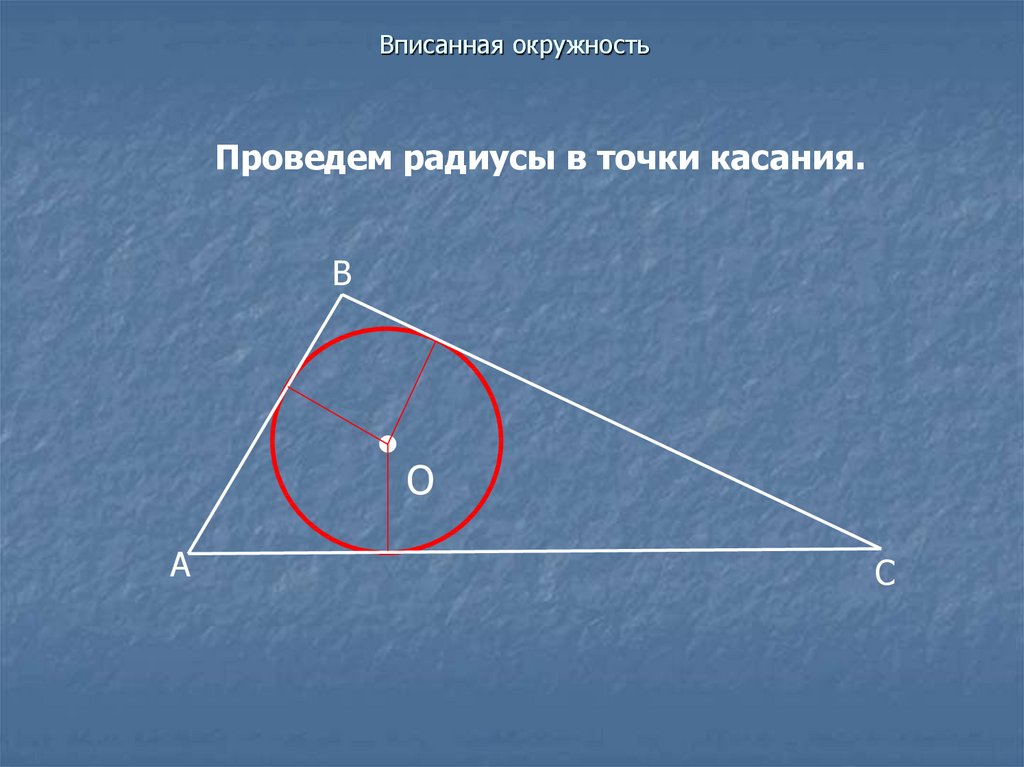
Проведем радиусы в точки касания.
В
О
А
С

9. Вписанная окружность

В
О
А
С

10. Вписанная окружность

В
О
А
С

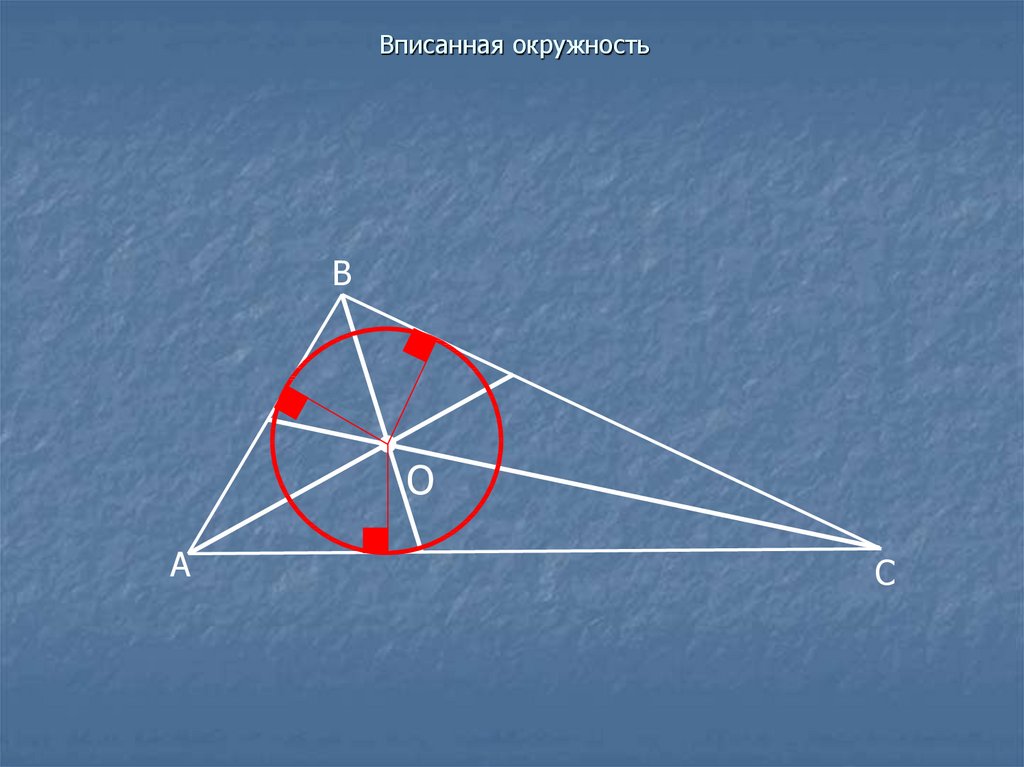
11. Вписанная окружность

В
О
А
С
АО - биссектриса угла А
ВО - биссектриса угла В
СО - биссектриса угла С

12. Вписанная окружность

Таким образом,
центр вписанной окружности – это точка
пересечения биссектрис треугольника,
радиус – это расстояние от центра
окружности до сторон треугольника.

13. Вписанная окружность

Для того, чтобы вписать окружность в
треугольник, надо:
1). Найти точку пересечения биссектрис
треугольника (центр окружности);
2). Опустить перпендикуляры из центра
окружности к сторонам треугольника
(радиус окружности);
3). Провести окружность.

14. Вписанная окружность

В
А
С

15. Вписанная окружность

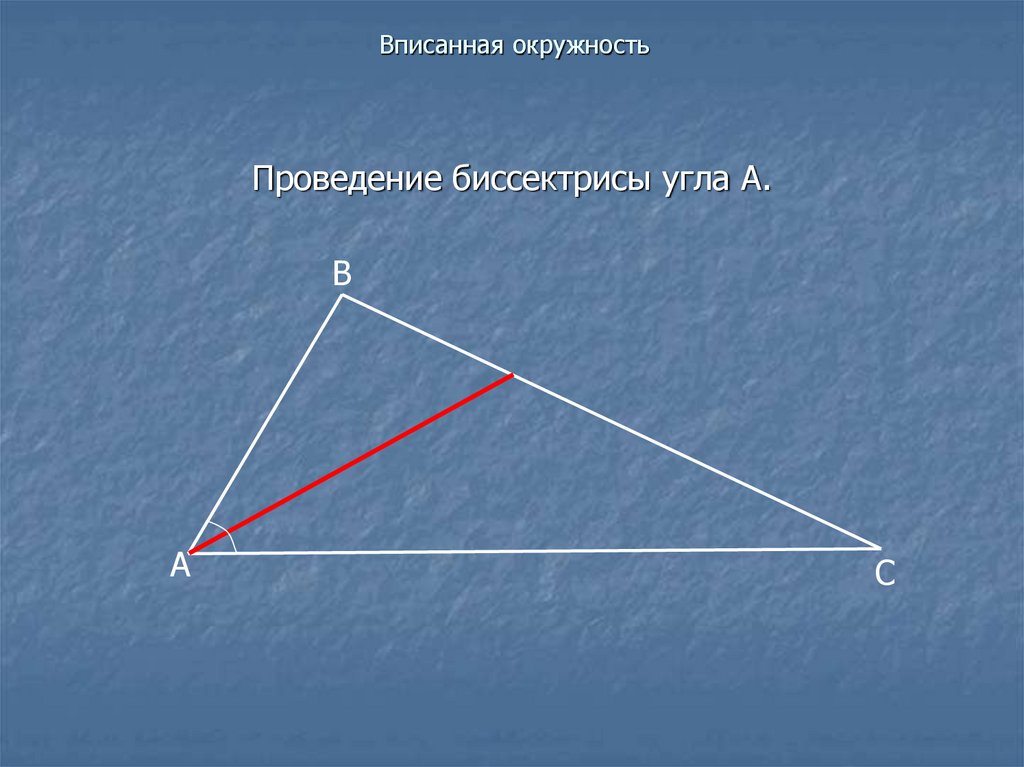
Проведение биссектрисы угла А.
В
А
С

16. Вписанная окружность

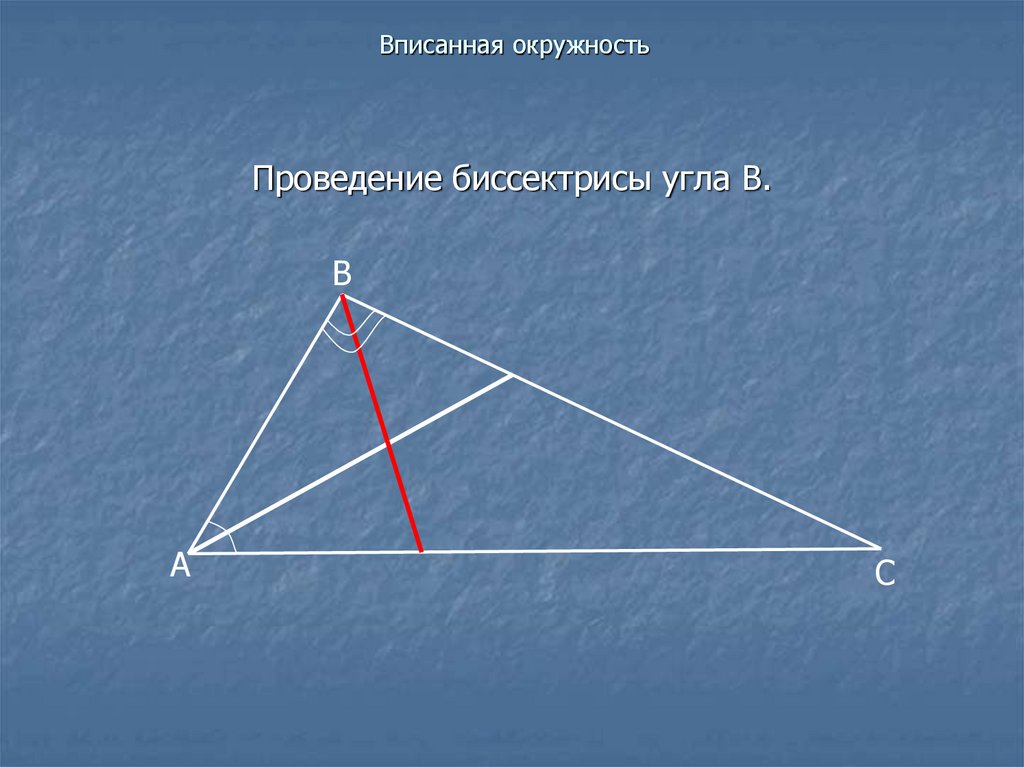
Проведение биссектрисы угла В.
В
А
С

17. Вписанная окружность

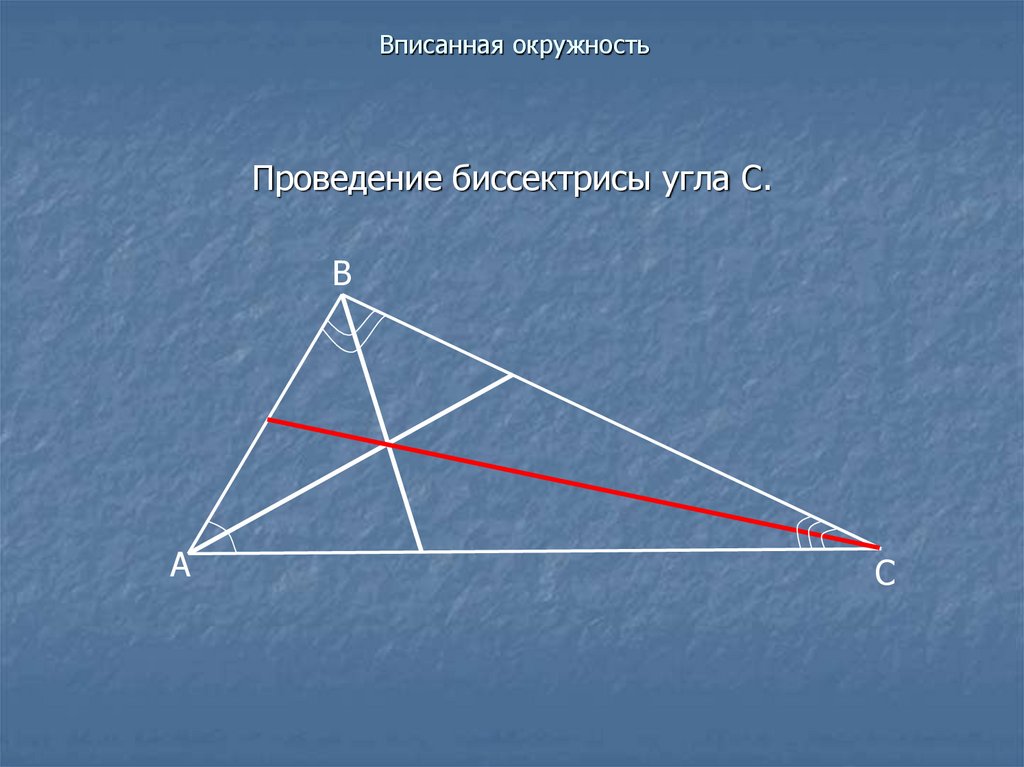
Проведение биссектрисы угла С.
В
А
С

18. Вписанная окружность

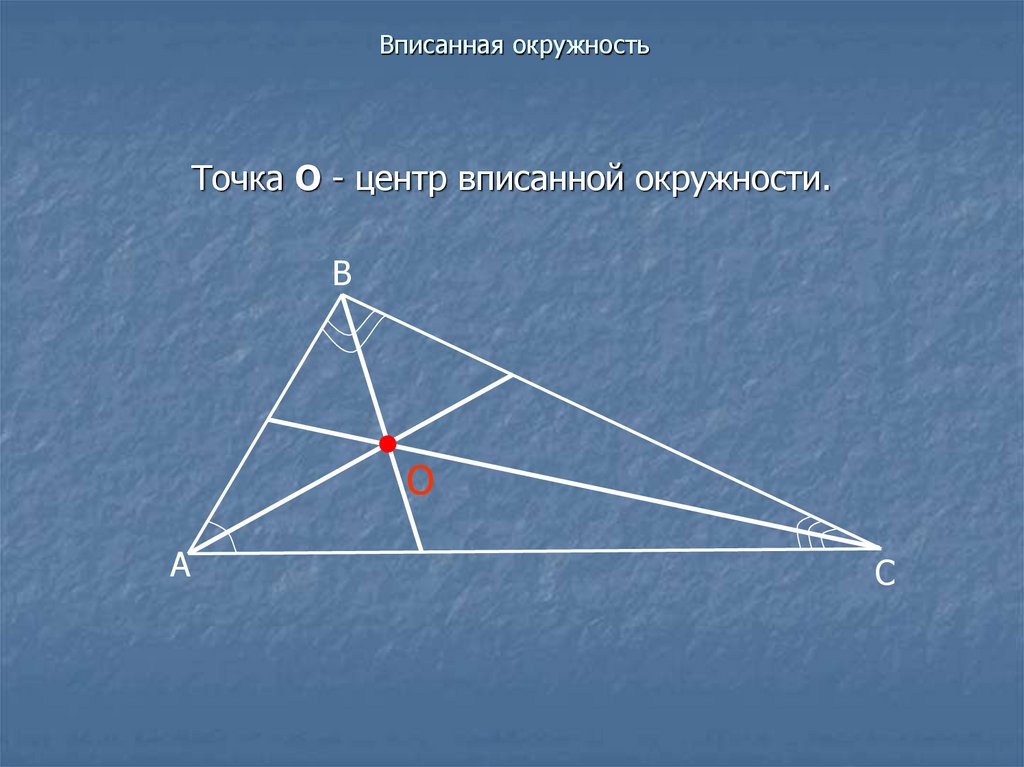
Точка О - центр вписанной окружности.
В
О
А
С

19. Вписанная окружность

Перпендикуляр из точки О к стороне АС.
В
О
А
С

20. Вписанная окружность

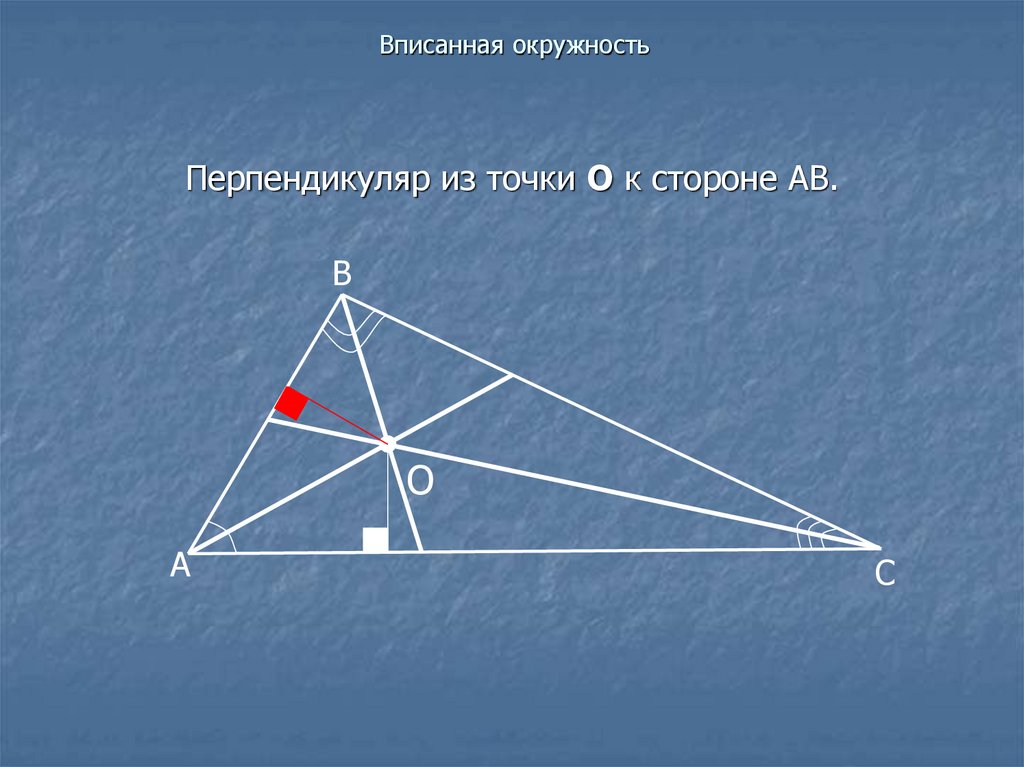
Перпендикуляр из точки О к стороне АВ.
В
О
А
С

21. Вписанная окружность

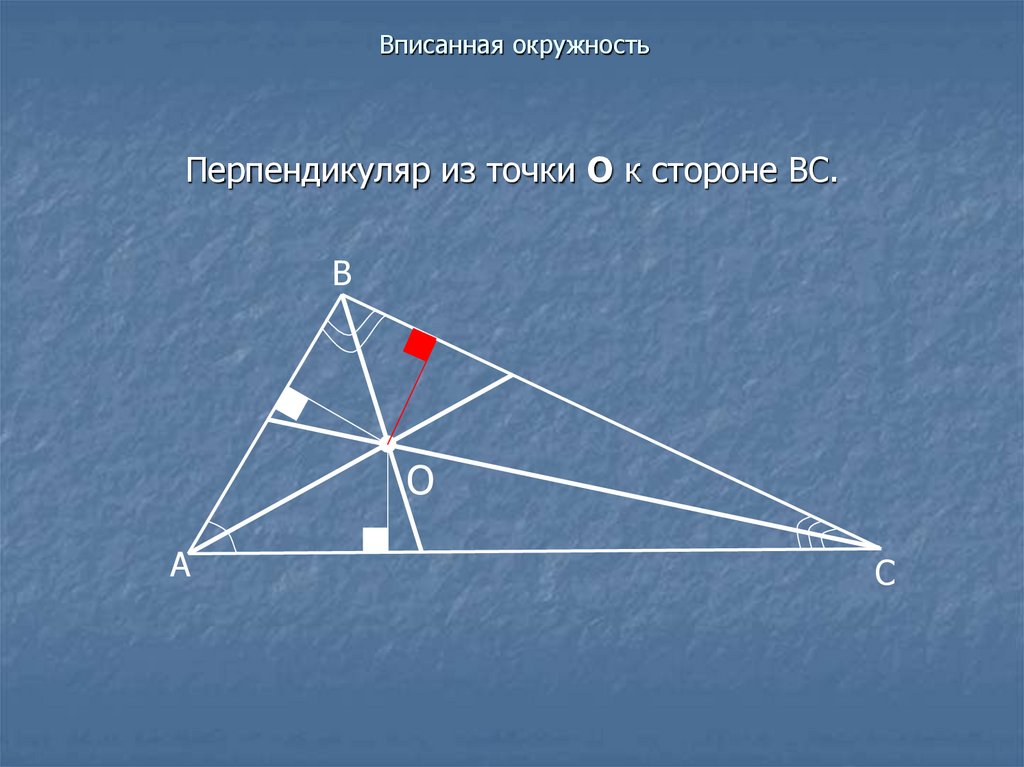
Перпендикуляр из точки О к стороне ВС.
В
О
А
С

22. Вписанная окружность

Окружность (О, r) – искомая.
В
r
А
О
С

23. Вписанная окружность

Теорема.
В любой треугольник можно вписать
окружность и при том только одну.

24.

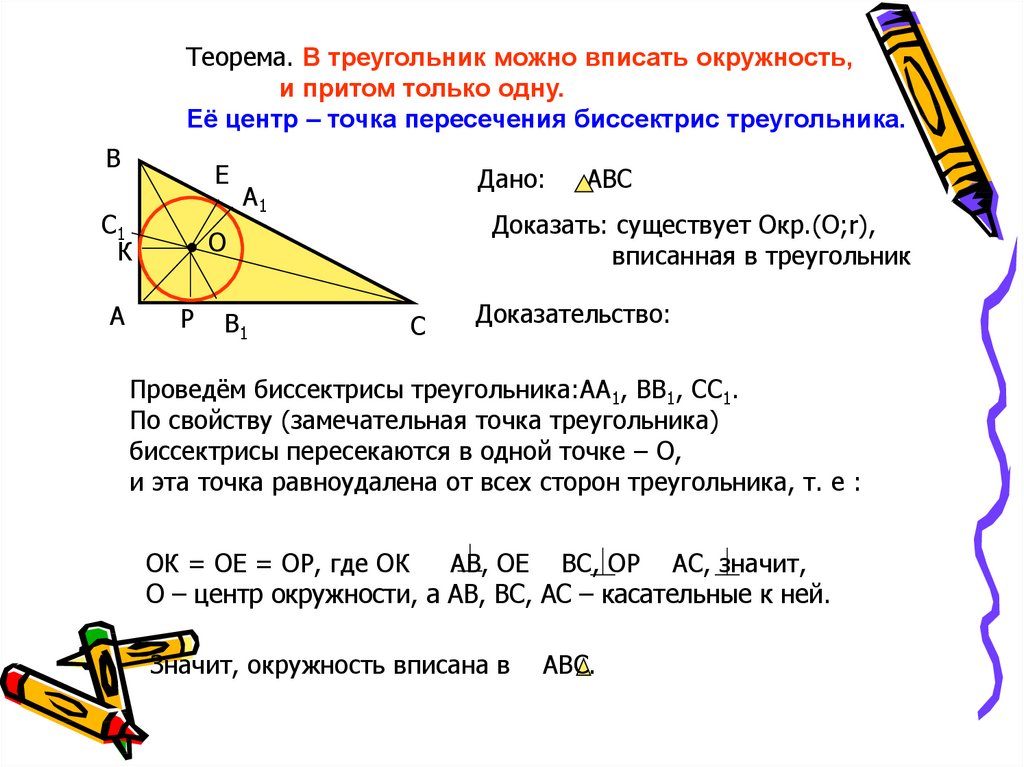
Теорема. В треугольник можно вписать окружность,
и притом только одну.
Её центр – точка пересечения биссектрис треугольника.
В
Е
С1
К
А
Дано:
А1
Доказать: существует Окр.(О;r),
вписанная в треугольник
О
Р
В1
АВС
С
Доказательство:
Проведём биссектрисы треугольника:АА1, ВВ1, СС1.
По свойству (замечательная точка треугольника)
биссектрисы пересекаются в одной точке – О,
и эта точка равноудалена от всех сторон треугольника, т. е :
ОК = ОЕ = ОР, где ОК
АВ, ОЕ ВС, ОР АС, значит,
О – центр окружности, а АВ, ВС, АС – касательные к ней.
Значит, окружность вписана в
АВС.

25.

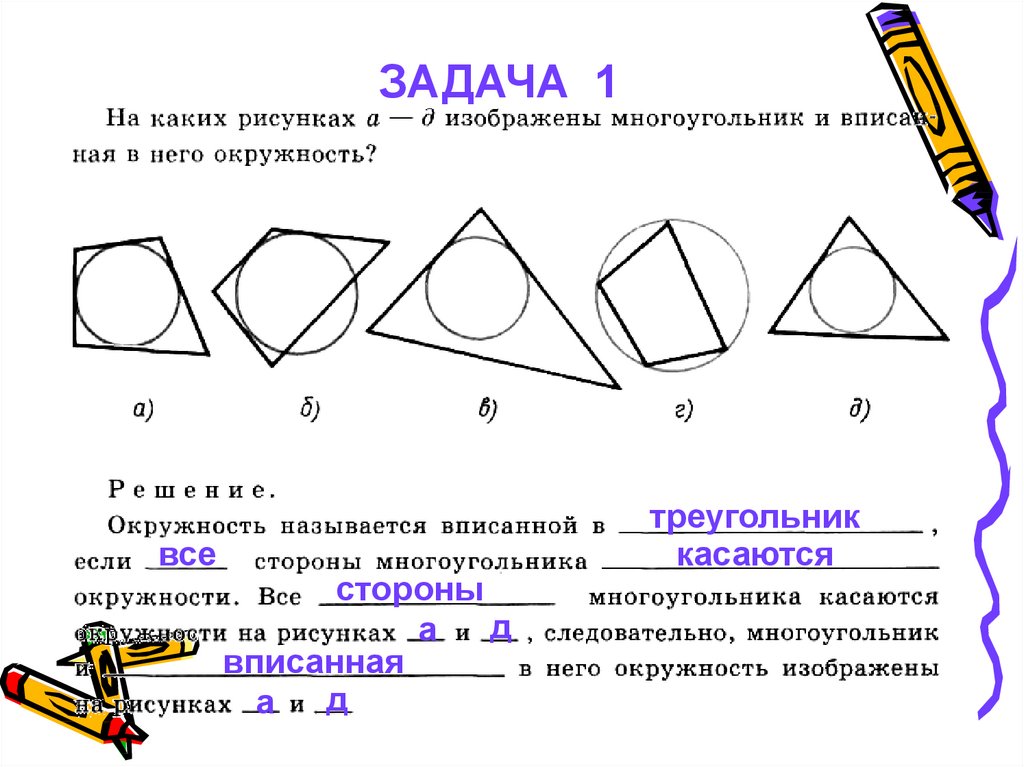
ЗАДАЧА 1
все
стороны
д
а
вписанная
а д
треугольник
касаются

26. Задача 2

ОКРУЖНОСТИ
ТОЧКИ
3
BT
6
HB+BT+AT
2
3+6
28
АМ
MC+СH
СH

27.

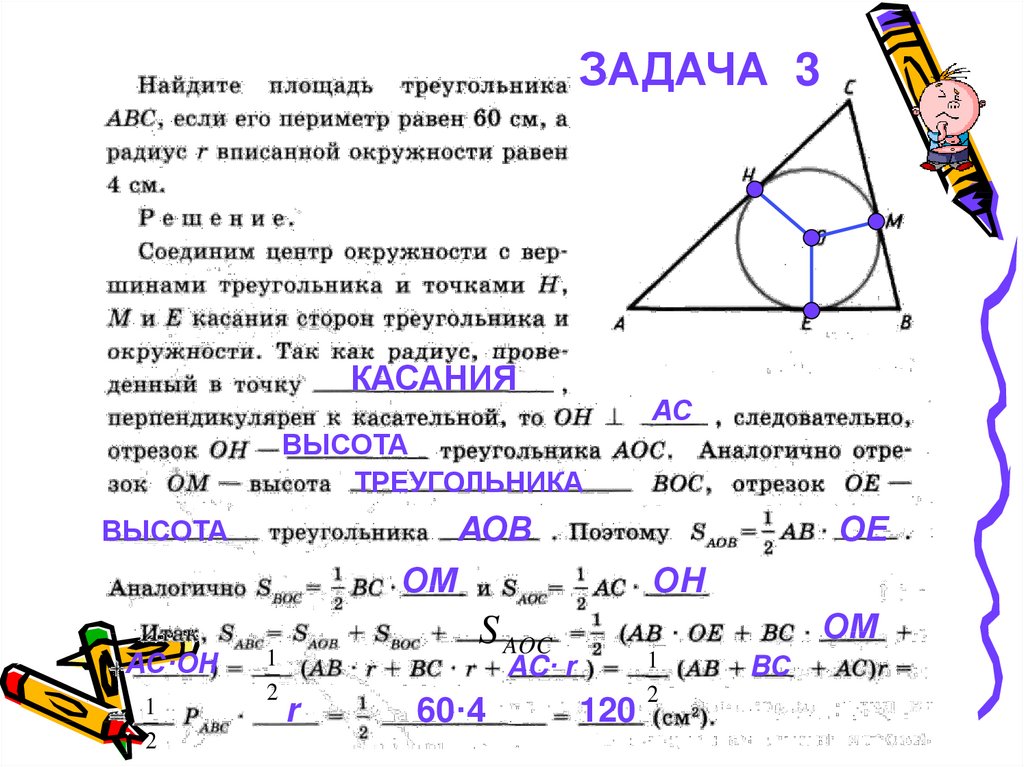
ЗАДАЧА 3
КАСАНИЯ
АС
ВЫСОТА
ТРЕУГОЛЬНИКА
АОВ
ВЫСОТА
ОЕ
ОМ
АС·OH
1
2
1
2
ОH
ОМ
S AOC
AC· r
r
60·4
120
1
2
BС

28. № 691

Дано: ABC равнобедренный
АС-основание
В
окр (О; R) вписанная
Точки K, N, D –
точки
касания.
ВК = 4 cm
КА = 3 cm
Найти PABC
N
K
O
А
D
С

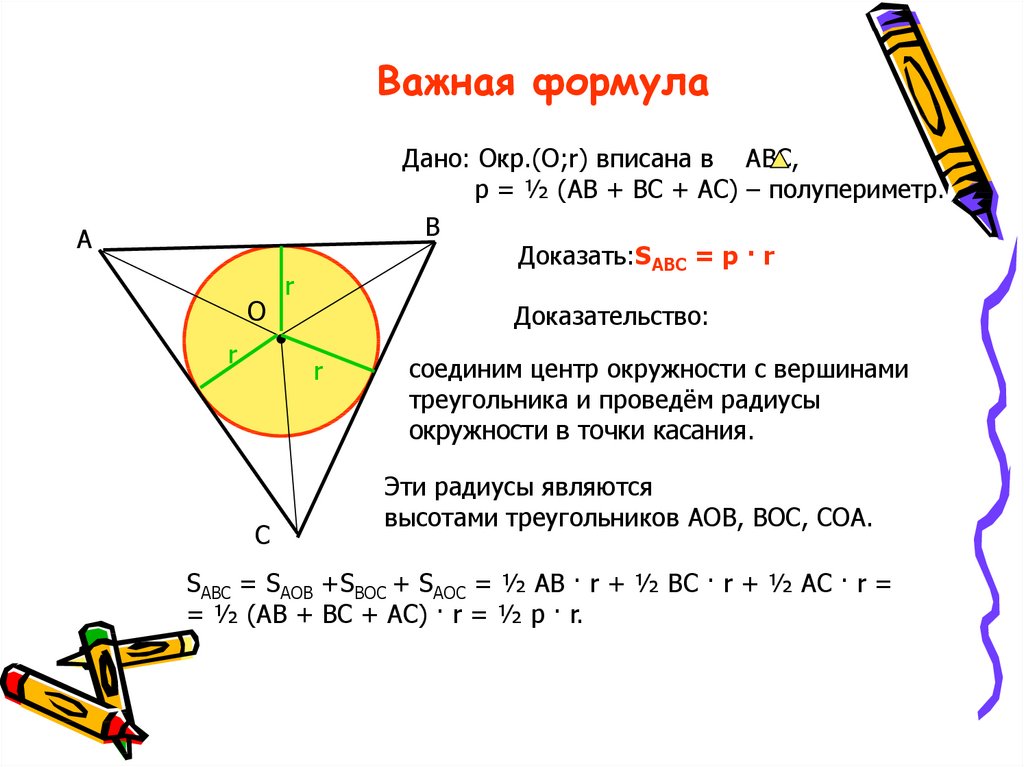
29. Важная формула

Дано: Окр.(О;r) вписана в АВС,
р = ½ (АВ + ВС + АС) – полупериметр.
В
Доказать:SABC = p · r
А
О
r
r
Доказательство:
r
С
соединим центр окружности с вершинами
треугольника и проведём радиусы
окружности в точки касания.
Эти радиусы являются
высотами треугольников АОВ, ВОС, СОА.
SABC = SAOB +SBOC + SAOC = ½ AB · r + ½ BC · r + ½ AC · r =
= ½ (AB + BC + AC) · r = ½ p · r.

30.

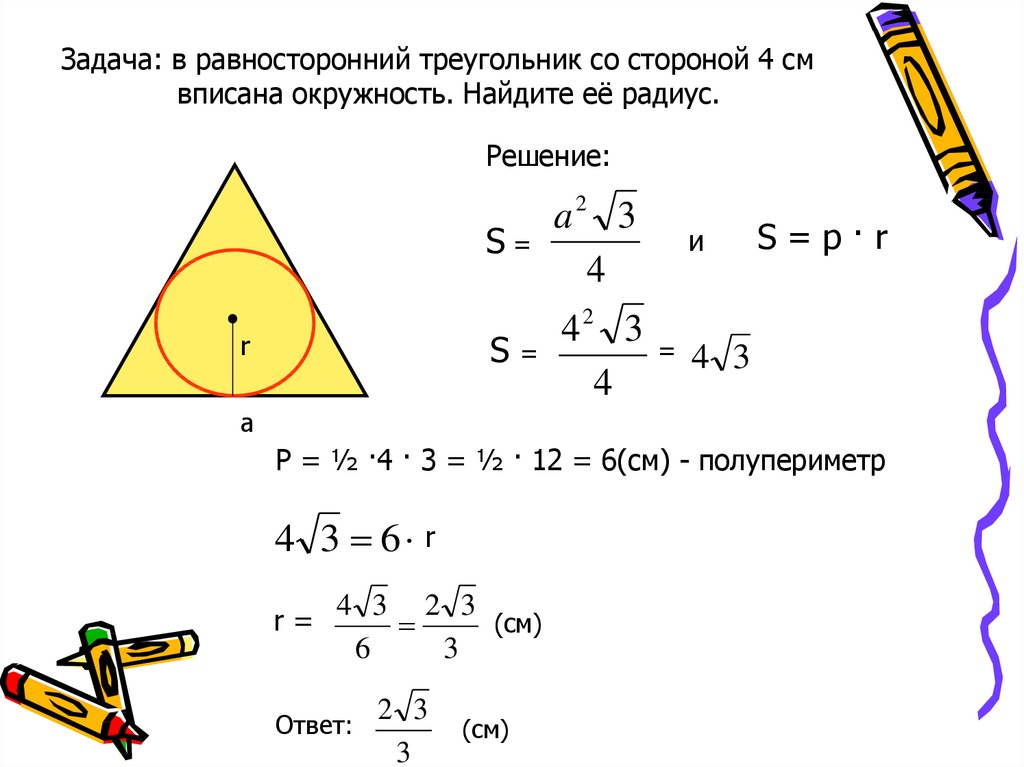
Задача: в равносторонний треугольник со стороной 4 см
вписана окружность. Найдите её радиус.
Решение:
S=
S
r
=
a2 3
4
4
2
3
4
и
=
S=p·r
4 3
а
P = ½ ·4 · 3 = ½ · 12 = 6(см) - полупериметр
4 3 6 r
r=
4 3 2 3
(см)
6
3
Ответ:
2 3
3
(см)

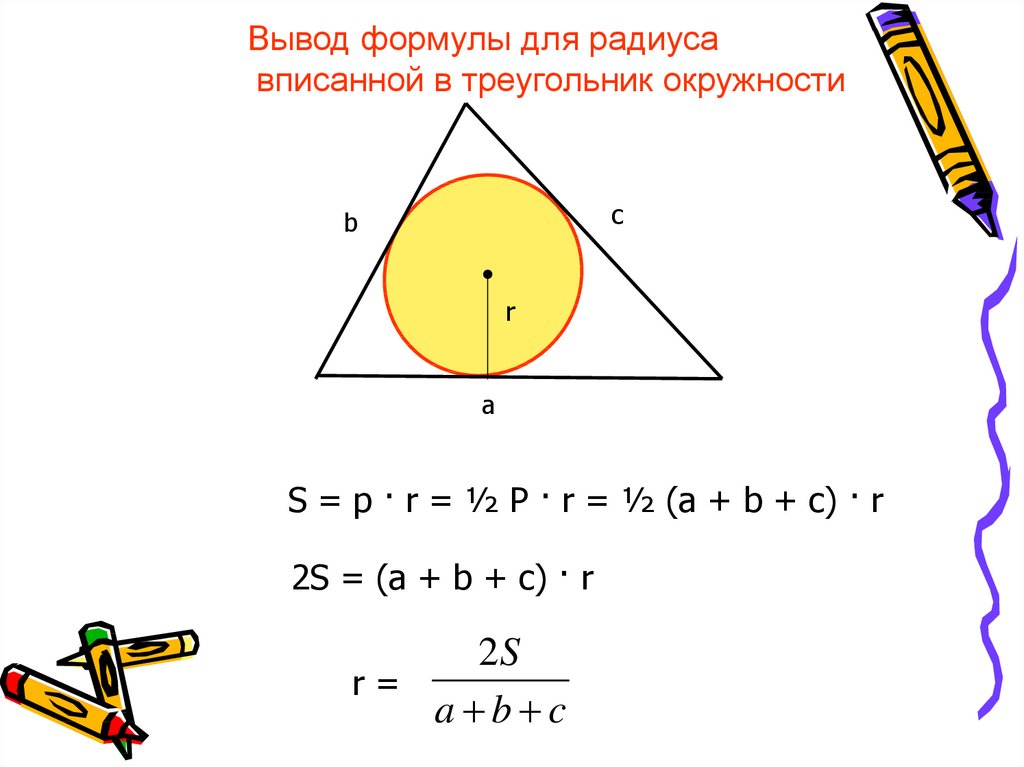
31.

Вывод формулы для радиуса
вписанной в треугольник окружности
c
b
r
a
S = p · r = ½ P · r = ½ (a + b + c) · r
2S = (a + b + c) · r
2S
r=
a b c

32.

Задача: в прямоугольный треугольник вписана окружность,
гипотенуза точкой касания делится на отрезки 6 см и 4 см.
Найдите радиус вписанной окружности.
А
Дано: АВС,
С = 900
Окр.(О;r) вписана,
АМ = 6 см, ВМ = 4 см
Найти: r.
6
Решение:
М
К
r
О r
4
r
С
В
Е
Т. к.
АВ = АМ + ВМ = 6 + 4 = 10(см)
Т. к. Окр.(O;r) вписана в АВС, то
АВ, АС,ВС – касательные и по свойству
касательных, проведённых из одной точки:
АМ = АК = 6 см, ВЕ = ВМ = 4 см, СК = СЕ
С = 900, то СКОЕ – квадрат, поэтому СК = СЕ = r.
АС= 6+ r, ВС = 4 + r
По теореме Пифагора: АС2 + ВС2 = АВ2
(6 + r)2 + (4 + r)2 = 102
Решив квадратное уравнение, получим r = 2 см
Ответ: 2 см
,

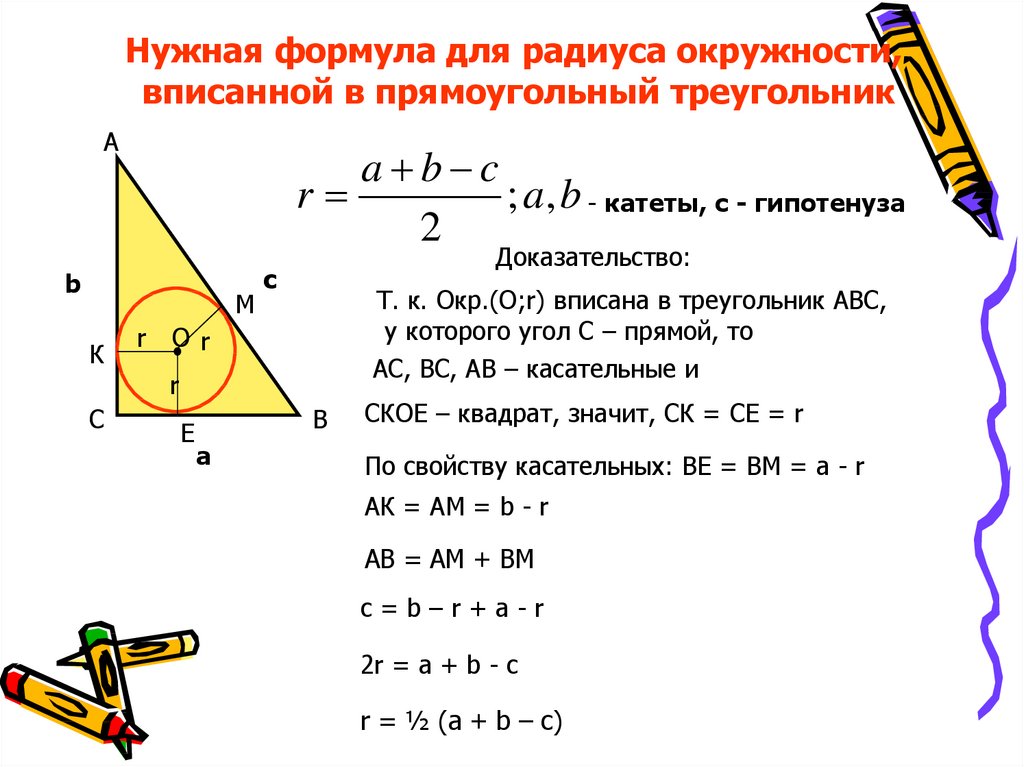
33.

Нужная формула для радиуса окружности,
вписанной в прямоугольный треугольник
А
a b c
r
; a, b - катеты, с - гипотенуза
2
b
М
К
С
r
Доказательство:
c
Т. к. Окр.(О;r) вписана в треугольник АВС,
у которого угол С – прямой, то
АС, ВС, АВ – касательные и
О r
r
Е
В
a
СКОЕ – квадрат, значит, СК = СЕ = r
По свойству касательных: ВЕ = ВМ = а - r
АК = АМ = b - r
AB = AM + BM
c=b–r+a-r
2r = a + b - c
r = ½ (a + b – c)