Теорема о трех перпендикулярах. Решение задач

1. ТЕМА УРОКА.

2.

Сформировать навык
применения теоремы
о трех
перпендикулярах
при решении задач.

3. Устная работа

Верно ли
следующее
утверждение:

4.

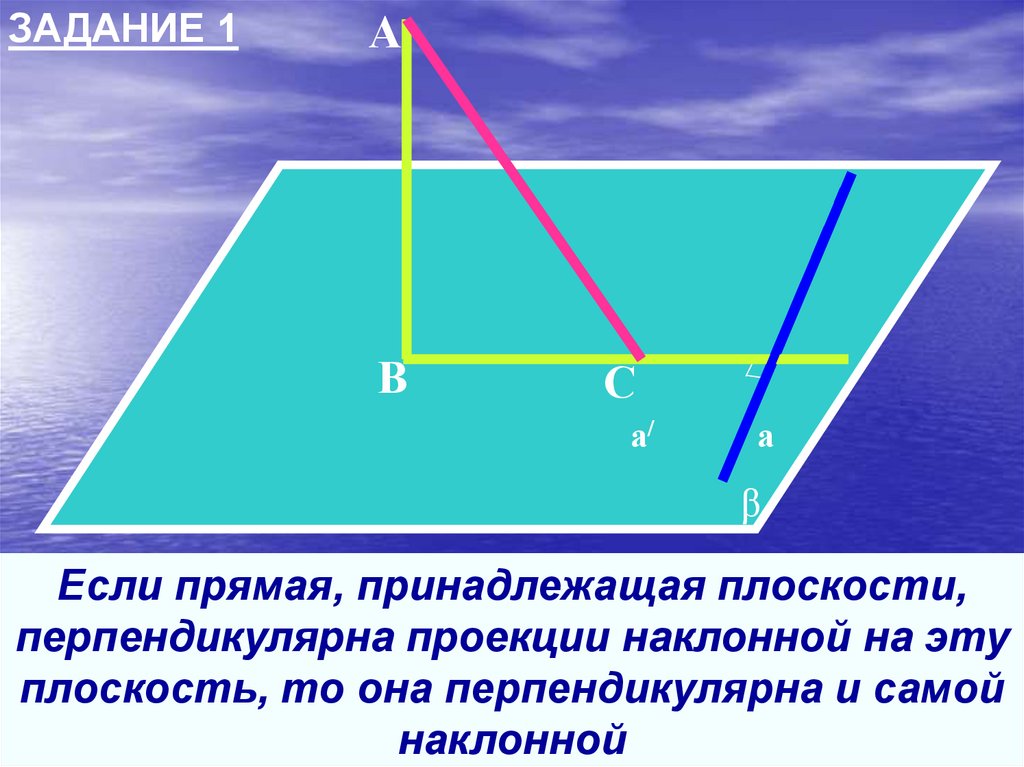
ЗАДАНИЕ 1
А
В
С
а/
а
β
Если прямая, принадлежащая плоскости,
перпендикулярна проекции наклонной на эту
плоскость, то она перпендикулярна и самой
наклонной

5.

ЭТО ВЕРНО!

6.

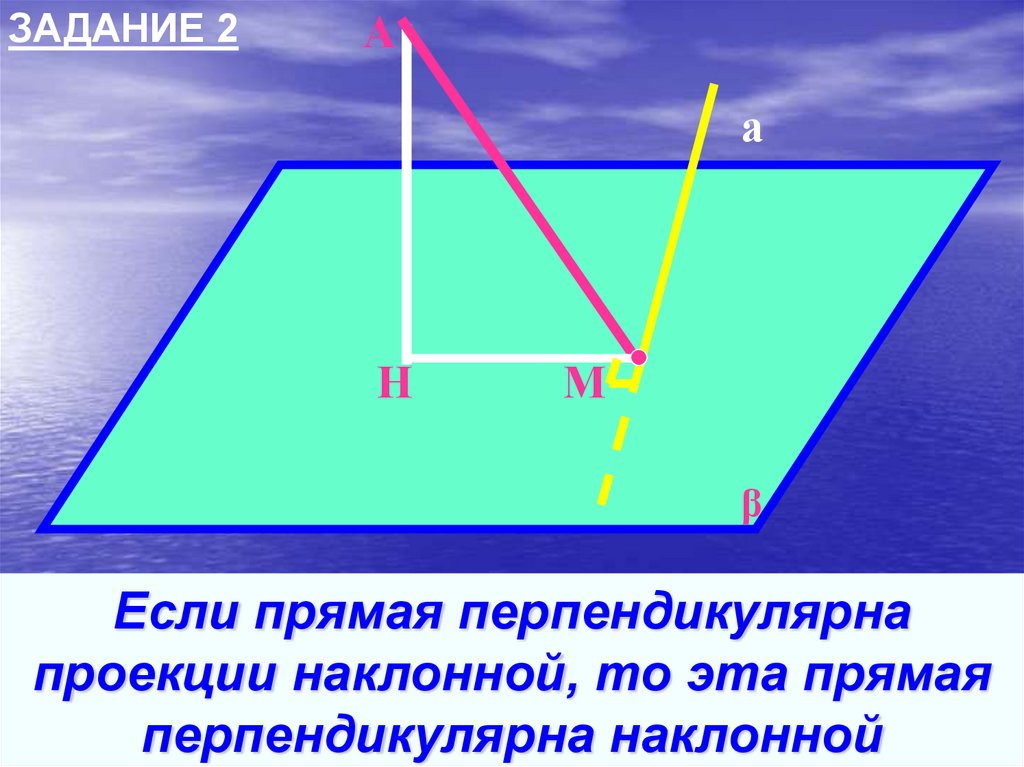
ЗАДАНИЕ 2
А
а
Н
М
β
Если прямая перпендикулярна
проекции наклонной, то эта прямая
перпендикулярна наклонной

7.

ЭТО НЕВЕРНО!
ПРЯМАЯ НЕ
ПРИНАДЛЕЖИТ
ПЛОСКОСТИ

8.

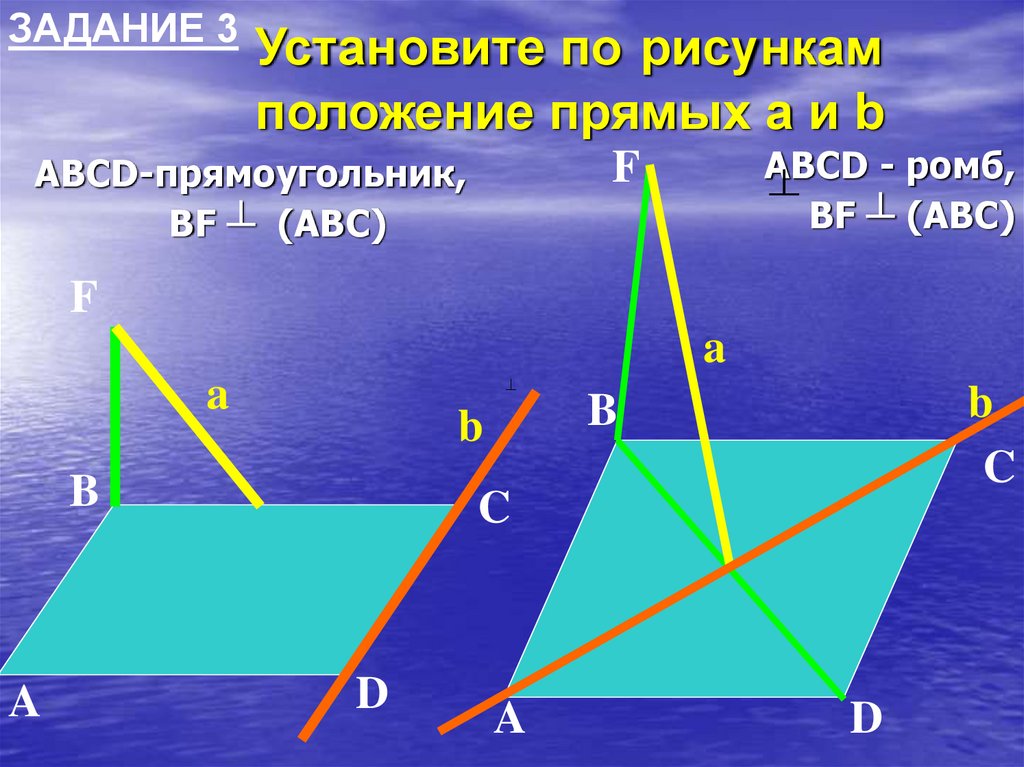
ЗАДАНИЕ 3
Установите по рисункам
положение прямых a и b
ABCD-прямоугольник,
BF ┴ (ABC)
ABCD
- ромб,
BF ┴ (ABC)
F
F
a
a
b
B
A
b
C
B
C
D
A
D

9.

Дано: ∟АВС = 600,
DB ┴ ABC, ∟A = 300
Доказать: CD ┴ AC
Задача
D1
B
600
A
300
C
α

10.

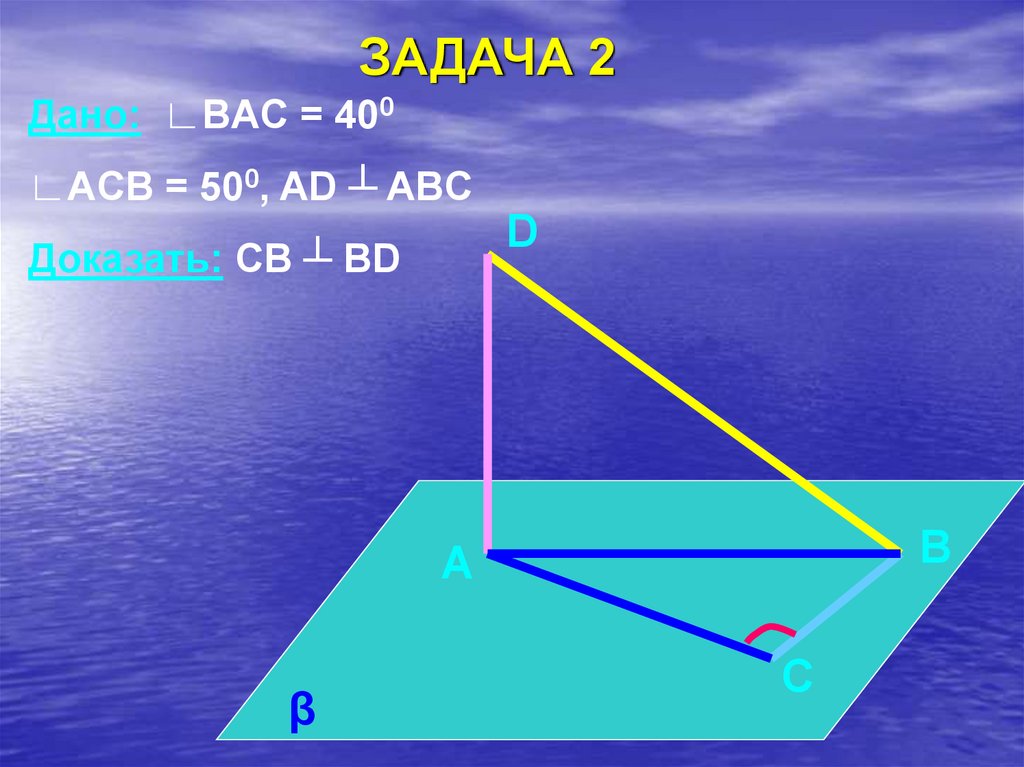
ЗАДАЧА 2
Дано: ∟BAC = 400
∟ACB = 500, AD ┴ ABC
D
Доказать: CB ┴ BD
B
A
β
C

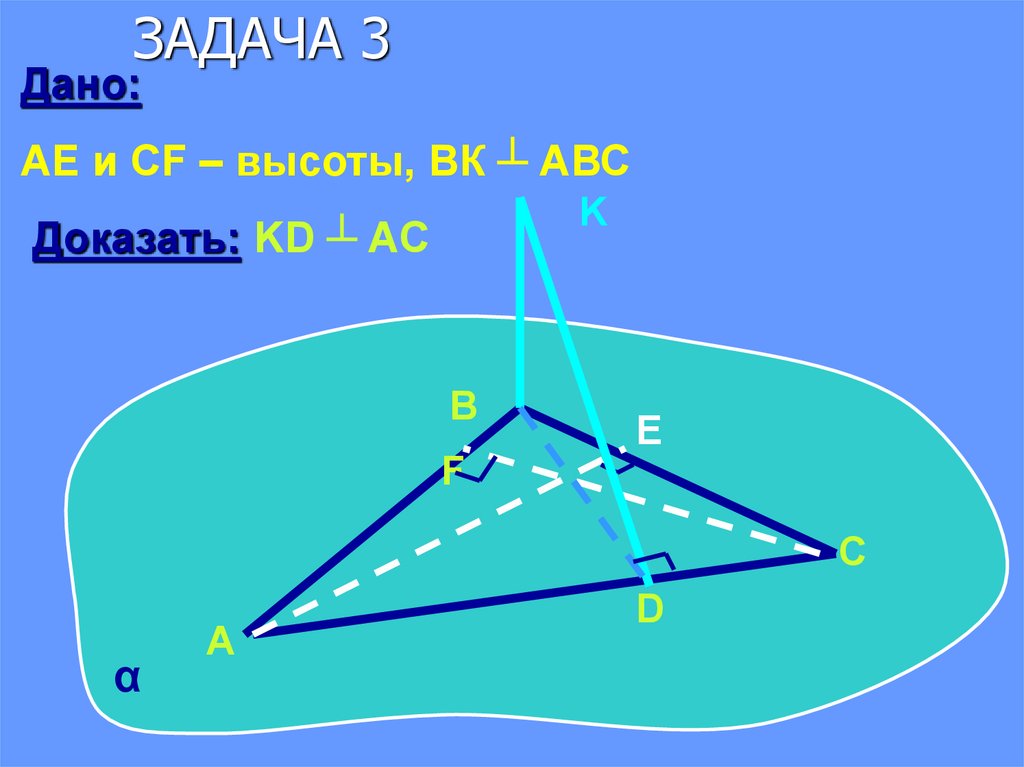
11. ЗАДАЧА 3

Дано:
AE и CF – высоты, ВК ┴ АВС
K
Доказать: KD ┴ AC
B
E
F
C
α
A
D

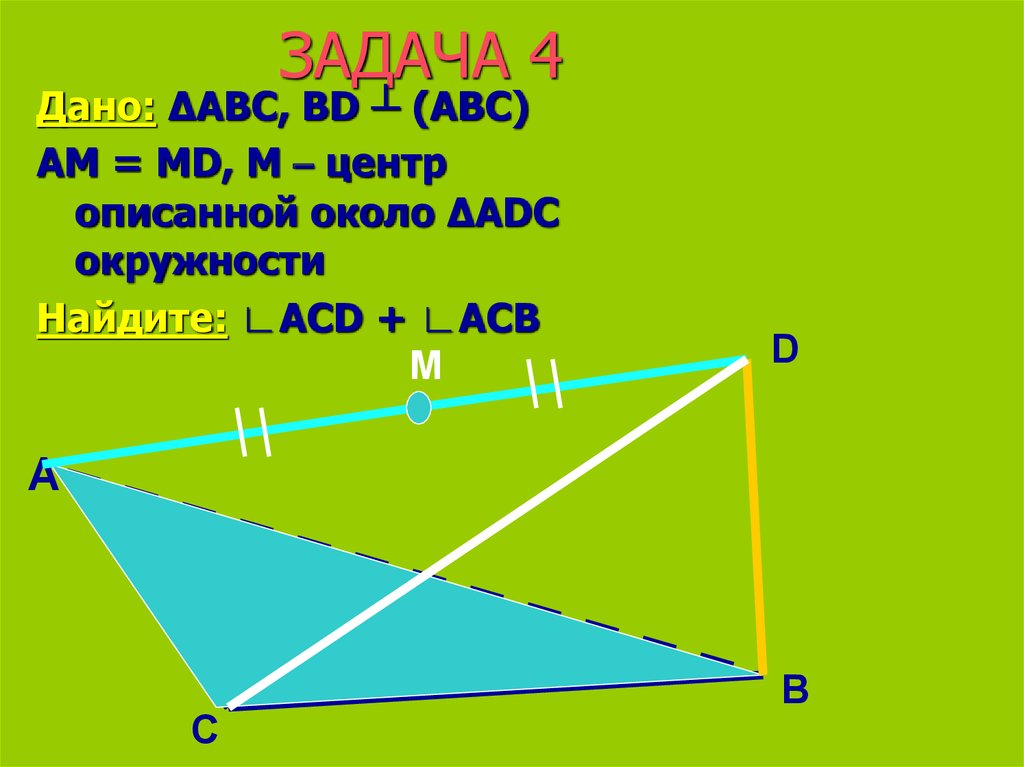
12. ЗАДАЧА 4

Дано: ∆ABC, BD ┴ (ABC)
AM = MD, M – центр
описанной около ∆ADC
окружности
Найдите: ∟ACD + ∟ACB
M
D
A
B
C

13. Самостоятельная работа

Вариант I
Вариант II
№154 (а)
№155

14. Домашнее задание №156, №159.