Соотношения между сторонами и углами прямоугольного треугольника

1. Геометрия.

8 класс.
Учитель: Самойлова Л. И.

2. Тема урока: «Соотношения между сторонами и углами прямоугольного треугольника»

Форма
урока: Вводный урок.
Цели урока: 1.Познакомить
учащихся с определениями и
сущностью тригонометрических
функций;
2.Формировать навыки тезисного
конспектирования;
3.Воспитывать наблюдательность,
развивать память, продолжить
работу над формированием
системы знаний .

3. Эпиграф урока:

«Коль
не знаешь правил – минус.
Если «О», то будет синус,
Если «И», то косинус.
Если знаешь – тебе плюс!

4. План вводного урока.

1.Прямоугольный треугольник, его
элементы, взаимосвязь.
2.Тригонометрические функции
«синус», «косинус».
3.Практическая пятиминутка:
упражнения на вычисление «синуса»,
«косинуса».
4. Тригонометрические функции
«тангенс», «котангенс».
5.Практическая пятиминутка:
упражнения на вычисление «тангенса»
и «котангенса».
6.Закрепление материала.

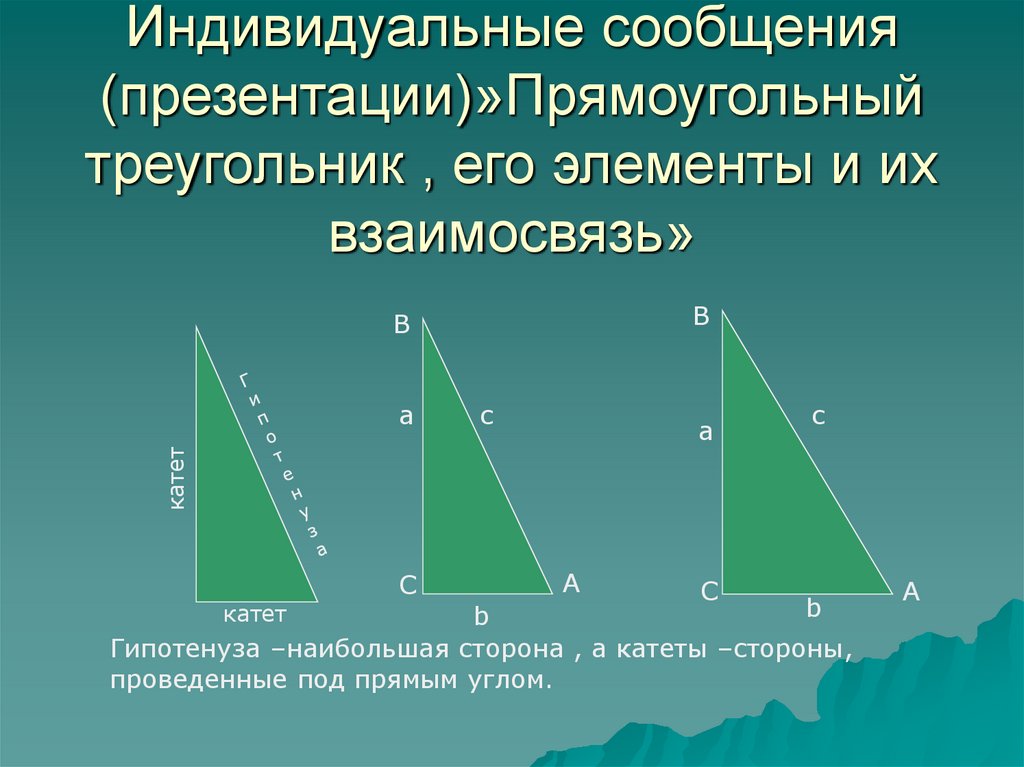
5. Индивидуальные сообщения (презентации)»Прямоугольный треугольник , его элементы и их взаимосвязь»

В
В
с
а
с
катет
а
С
А
С
b
b
Гипотенуза –наибольшая сторона , а катеты –стороны,
проведенные под прямым углом.
катет
А

6. Взаимосвязь между элементами прямоугольного треугольника.

Угол А – острый, угол В –острый, угол С
– прямой. В
с
а
С
b
А
Напротив А катет а – противолежащий.
Рядом прилег катет b – прилежащий.
Напротив В катет b – противолежащий.
Рядом прилег катет а –прилежащий.

7. Вывод:

Острый
угол прямоугольного
треугольника зависит от
гипотенузы, от катетов.
Примечание:
«Зная длины сторон прямоугольного
треугольника можно вычислить его
острый угол. Но для этого надо
знать тригонометрические
функции: «синус»,
«косинус»,»тангенс», «котангенс».

8. Эпиграф урока:

«Коль
не знаешь правил – минус.
Если «О», то будет синус,
Если «И», то косинус.
Если знаешь – тебе плюс!

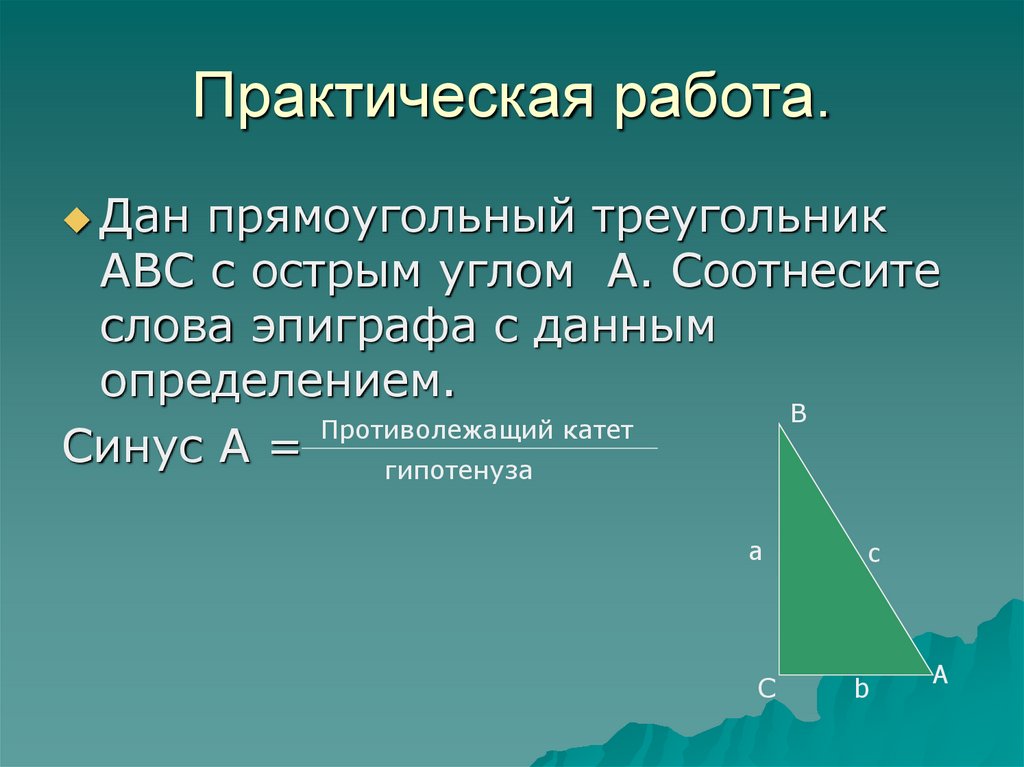
9. Практическая работа.

Дан
прямоугольный треугольник
АВС с острым углом А. Соотнесите
слова эпиграфа с данным
определением.
B
Противолежащий катет
Синус А =
гипотенуза
а
C
с
b
А

10. Практическая работа (продолжение)

Дан
прямоугольный треугольник
АВС с острым углом А.
Задание: соотнесите слова
эпиграфа с данным определением.
Прилежащий катет
Косинус А =
гипотенуза
В
с
a
С
b
A

11. Обозначение:

Sin
А - синус острого угла.
Cos А- косинус острого угла.
Формулы:
с
а
Sin
А =a/c;
Cos А = b /с.
b
А
А

12. Работа в парах.

Дан
треугольник АВС с острым
углом В.
Задание: Запишите формулы для
определения синуса и косинуса
В
В
В В
В
для угла В.
(про / гип. = ?)
Sin B =
Cos В =
(при / гип. =? )
В
В

13. Самостоятельная работа (практическая пятиминутка)

Задание.
Дан прямоугольный
треугольник АВС с острым углом А
и сторонами а = 4, b = 3.Найдите:
В
1)Sin A =
Cos A =
c
a
2)Чему равно выражение:
Sin2 A + Cos2 A =
С
А
b

14. Ответы:

1. Ответ: Sin A = 4/5
Cos A = 3/5.
2. Ответ: Sin2 A + Cos2 A = 1.
Это основное тригонометрическое
тождество.

15. Тригонометрические функции «тангенс» и «котангенс».

Определение:
Sin A
tg A = a /b или tg A =
Cos A
Cos A
ctg A = b/а или ctg A =
Sin A
В
с
а
С
b
A

16. Практическая пятиминутка

Дан
прямоугольный треугольник
АВС с острым углом А. Известно,
что сторона ВС = 2/3, а АС = 1/3.
Найдите: tg A = ? ctg A = ?
В
с
а
С
b
А

17. Закрепление материала.

1.Зачитать
определения
тригонометрических функций.
2.Повторить определения устно.
3. Озвучить обобщенный опорный
конспект «Тригонометрические
функции».

18. Домашнее задание.

1.Занести записи определений и
формул в справочник.
2. Параграф 4 .п.66.