Similar presentations:
Теорема Пифагора
1. Урок 2 Теорема Пифагора
Сегодняшний урок – урок закреплениятеоремы Пифагора, знакомство с
египетским треугольником и
пифагорейскими треугольниками.
2. Проверка домашнего задания
1). Сформулировать и доказатьтеорему Пифагора.
2). Привести еще одно доказательство
теоремы Пифагора путем построения
квадратов на сторонах треугольника.
3. Доказательство теоремы Пифагора путем построения квадратов на сторонах треугольника.
В Древней Индии, доказывая теорему,часто приводили только рисунок и
сопровождали его лишь одним словом
«Смотри».
Сравнить рисунки нетрудно, а в них вся
суть доказательства.
4. Устная работа
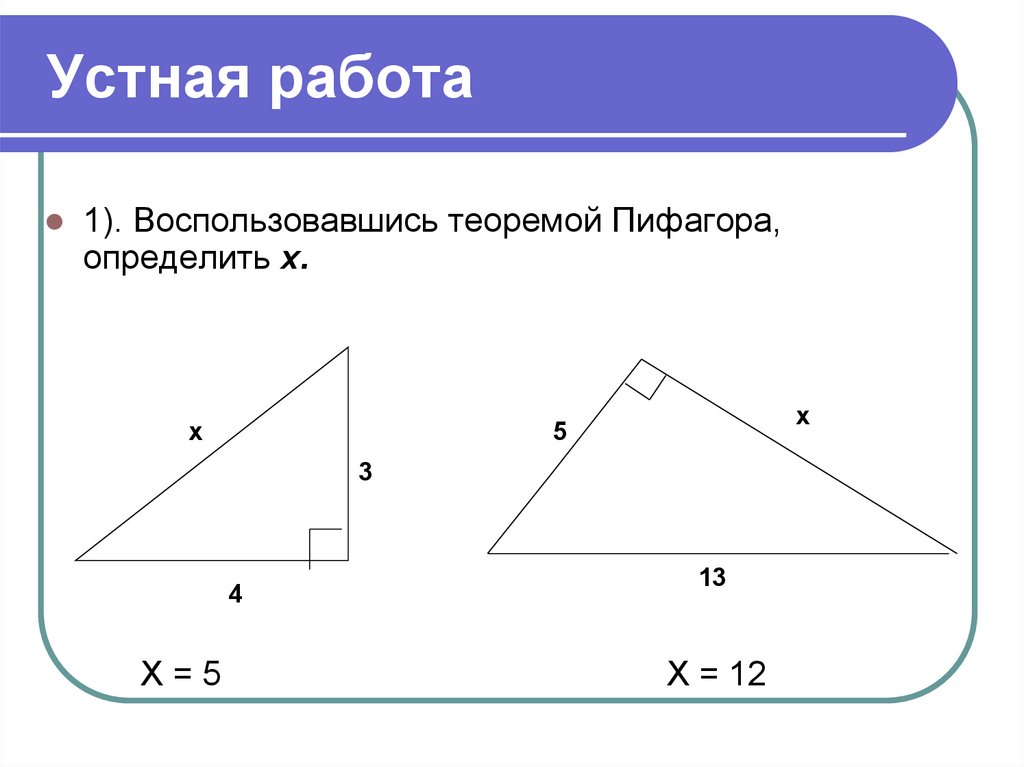
1). Воспользовавшись теоремой Пифагора,определить х.
х
х
5
3
4
Х=5
13
Х = 12
5. Устная работа
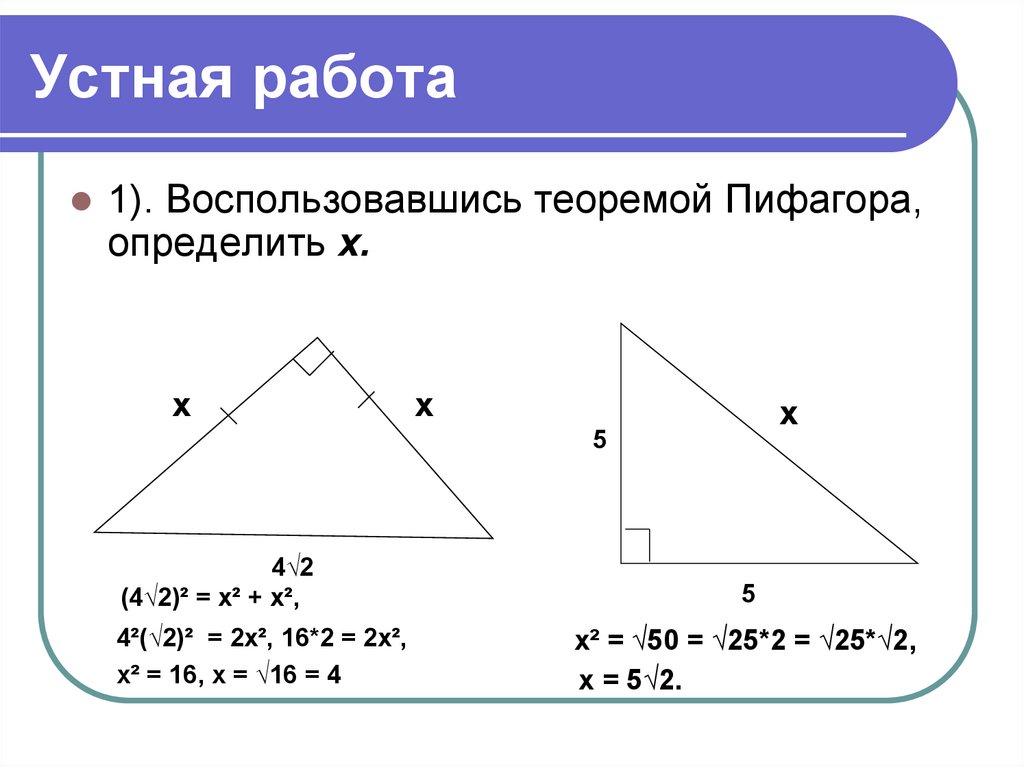
1). Воспользовавшись теоремой Пифагора,определить х.
х
х
х
5
4√2
(4√2)² = х² + х²,
4²(√2)² = 2х², 16*2 = 2х²,
х² = 16, х = √16 = 4
5
х² = √50 = √25*2 = √25*√2,
х = 5√2.
6. Устная работа
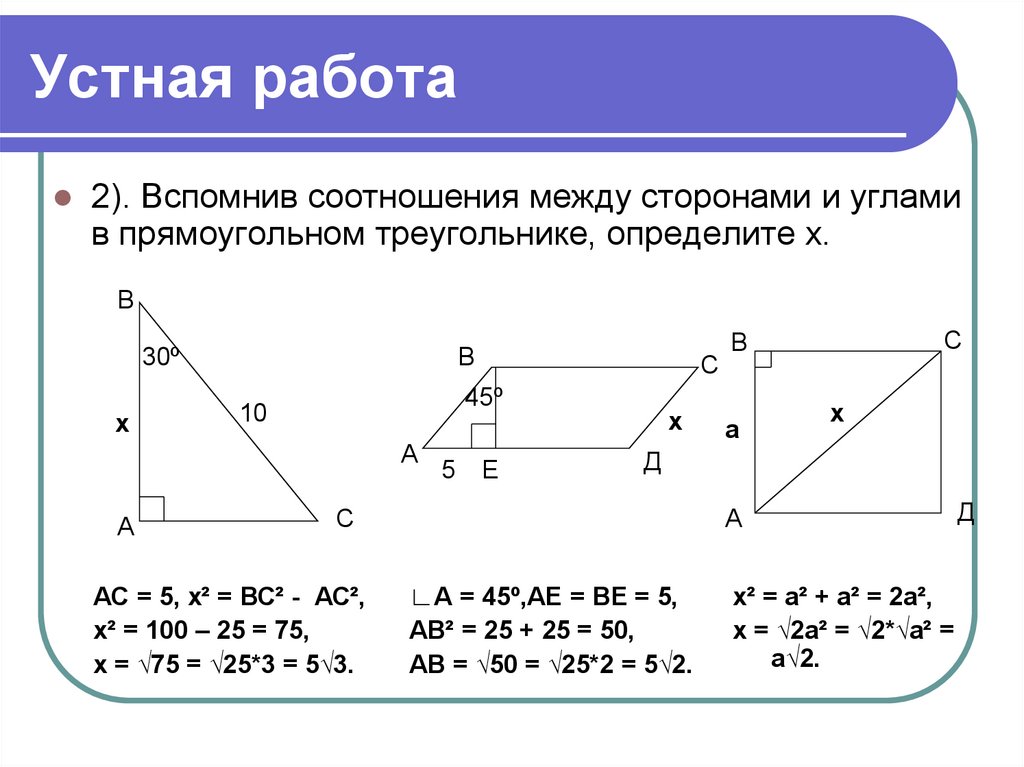
2). Вспомнив соотношения между сторонами и угламив прямоугольном треугольнике, определите х.
В
30º
х
В
45º
10
А
А
С
5
Е
х
а
х
Д
С
АС = 5, х² = ВС² - АС²,
х² = 100 – 25 = 75,
х = √75 = √25*3 = 5√3.
С
В
А
∟А = 45º,АЕ = ВЕ = 5,
АВ² = 25 + 25 = 50,
АВ = √50 = √25*2 = 5√2.
х² = а² + а² = 2а²,
х = √2а² = √2*√а² =
а√2.
Д
7.
В тетрадях № 494 (из учебника)8. Изучение новой темы
Египетский треугольник.Треугольник со сторонами
3, 4, 5 назвали
египетским. Название
такое получил потому, что
еще в Древнем Египте
для построения прямых
углов на местности
использовали именно этот
способ.
9. Египетский треугольник
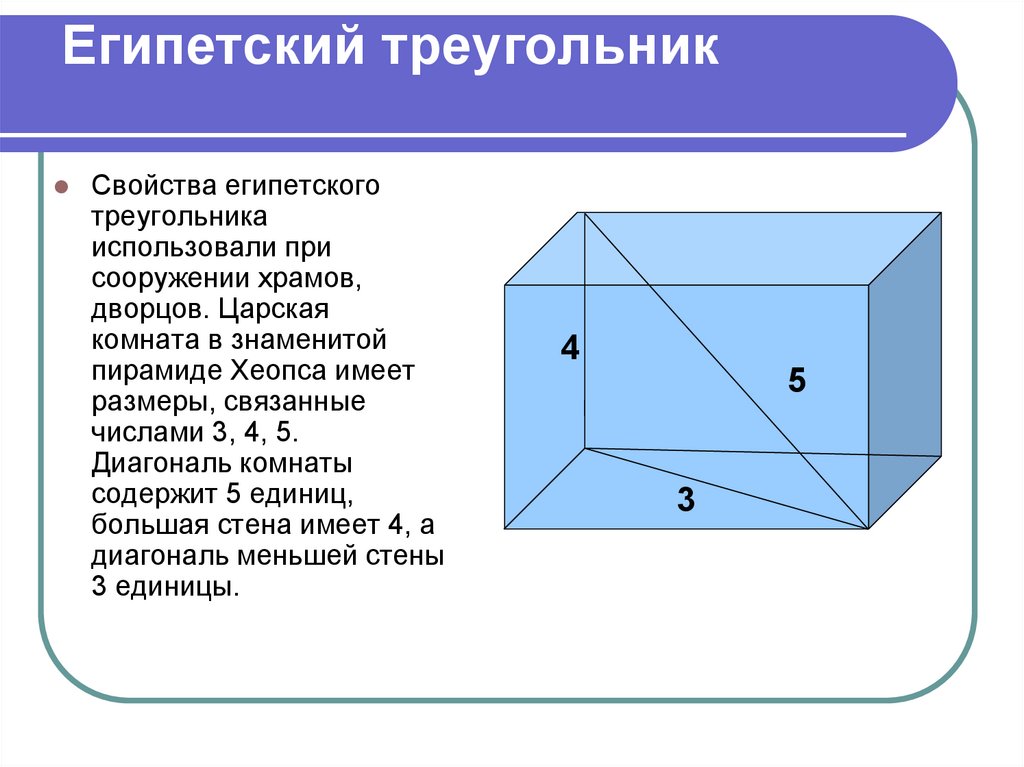
Свойства египетскоготреугольника
использовали при
сооружении храмов,
дворцов. Царская
комната в знаменитой
пирамиде Хеопса имеет
размеры, связанные
числами 3, 4, 5.
Диагональ комнаты
содержит 5 единиц,
большая стена имеет 4, а
диагональ меньшей стены
3 единицы.
4
5
3
10. Пифагоровы треугольники
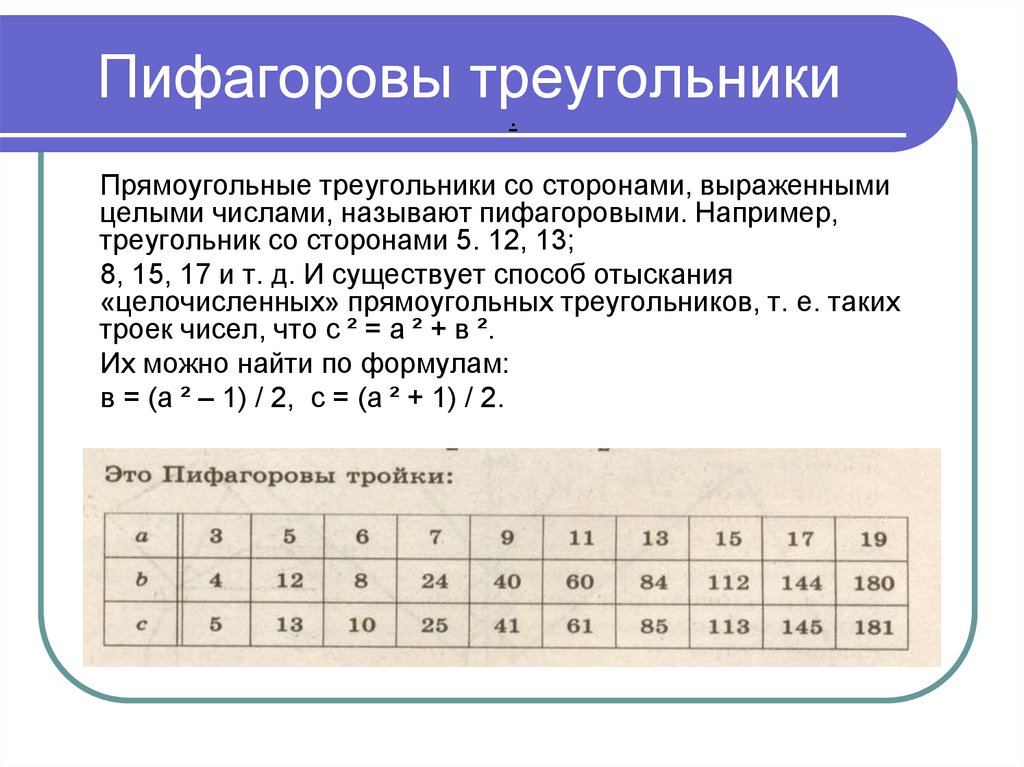
.Прямоугольные треугольники со сторонами, выраженными
целыми числами, называют пифагоровыми. Например,
треугольник со сторонами 5. 12, 13;
8, 15, 17 и т. д. И существует способ отыскания
«целочисленных» прямоугольных треугольников, т. е. таких
троек чисел, что с ² = а ² + в ².
Их можно найти по формулам:
в = (а ² – 1) / 2, с = (а ² + 1) / 2.
11. Теорема, обратная теореме Пифагора
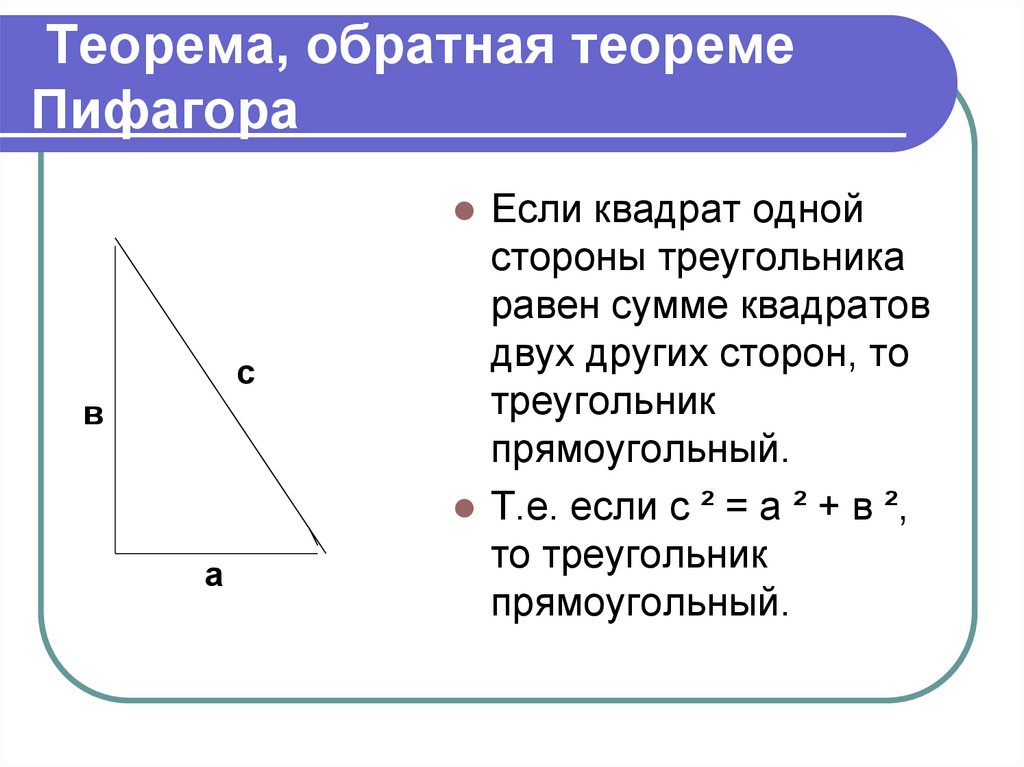
Если квадрат однойстороны треугольника
равен сумме квадратов
двух других сторон, то
треугольник
прямоугольный.
Т.е. если с ² = а ² + в ²,
то треугольник
прямоугольный.
с
в
а
12. Самостоятельная работа
Дается на карточках (4 варианта).Второе задание дополнительное,
предназначенное для сильных
учащихся. Можно использовать
микрокалькуляторы.
13. Задание на дом
1. § 3, п. 54, 55,2. №№ 488(б), 498(а,б,г)







 mathematics
mathematics