Similar presentations:
Пифагор и его теорема
1. МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА с. ПЕРУНЬ» Индивидуальный итоговый
проект«Пифагор и его теорема»
Проект выполнила
ученица 9 класса:
Филиппова Ксения.
Руководитель
Учитель математики:
Алексеева Т.А.
Петрунь
2021
2. Содержание: 1. Введение. 2. Основная часть. Глава 1. Теорема Пифагора. А) О теореме Пифагора. Б) Различные доказательства
Содержание:1. Введение.
2. Основная часть.
Глава 1. Теорема Пифагора.
А) О теореме Пифагора.
Б) Различные доказательства теоремы Пифагора.
Глава 2. Пифагоровы тройки.
3. Заключение.
4. Литература.
5. Приложение.
3.
1. Введение.В курсе геометрии есть интересная теорема, известная с древнейших
времён:
«Сумма квадратов катетов прямоугольного треугольника равна
квадрату гипотенузы».
Обычно открытие этого утверждения приписывают древнегреческому
философу и математику Пифагору (VI век до н.э). Но изучение древних
рукописей показало, что это утверждение было известно задолго до
рождения Пифагора.
Изучая историю теоремы, я решила выяснить: существуют ли другие
доказательства этой теоремы.
Каково значение этой теоремы в жизни людей? Какую роль сыграл Пифагор
в развитии математики?
Теорема Пифагора в математике является одной из главных теорем. С ее
помощью решается огромное количество задач.
Пифагор – едва ли не самый популярный ученый за всю историю
человечества. Наверное, нет человека, который не слышал о Пифагоре и о
его теореме. Тема была актуальна в прошлом, актуальна и в наши дни.
Каждый интересующийся математикой пытается найти новое доказательство
теоремы Пифагора.
4.
Цель и задачи: рассмотреть различные доказательства теоремыПифагора и ее применения, узнать о тройках Пифагора.
Проект состоит из двух глав:
Глава 1. «Теорема Пифагора».
Глава 2. «Пифагоровы тройки».
Для написания работы источником послужили книги Волошина А.В.
и Скопца состояла в том, что прочитать о Пифагоре практически
невозможно, так как на русском языке практически нет ни одной
современной книги о Пифагоре – ни научной, ни популярной. В
источниках говориться лишь о двух книгах – это монография
Чанышева А.Н. З.А. «Геометрические миниатюры» и другие книги.
Сложность «Италийская философия» и Жнудь Л.Я. «Пифагор и его
школа».
Вторая сложность состояла в отборе материала, так как работа имеет
свои размеры, поэтому необходимо было определиться, какие факты
отразить в работе.
Работа носит исследовательский характер.
5.
2. Основная часть.Глава 1. Теорема Пифагора.
А) О теореме Пифагора.
Пифагор (570 – 490 гг. до н. э.) – выдающийся философ, математик и
мистик Древней Греции, вклад в науку которого неоценим и по сей день.
Теорема Пифагора, таблица умножения и многие другие открытия,
сделанные Пифагором ещё до нашей эры, пронеслись сквозь тысячелетия и,
наверное, вряд ли когда-нибудь перестанут быть актуальными среди людей.
Жизнь Пифагора неотделима от тайн и легенд, в которых его неоднократно
называли чудотворцем и даже полубогом. Пифагор считал, что в основе
любой вещи лежит число, и изучить мир – значит изучить управляющие им
числа. Он был великим математиком и создал одну из самых известных
теорем: квадрат гипотенузы равен сумме квадратов катетов. Открытие
теоремы Пифагором окружено ореолом легенд.
Считается, что сам Пифагор не доказывал эту теорему, он лишь передал
людям знание. И вполне успешно! На данный момент в современном
научном мире существует уже более 300 доказательств теоремы Пифагора.
До сих пор в школах всего мира, самой популярной теоремой считается
теорема Пифагора: a2+b2=c2. Каждый школьник помнит, что
«пифагоровы штаны, во все стороны равны».
6.
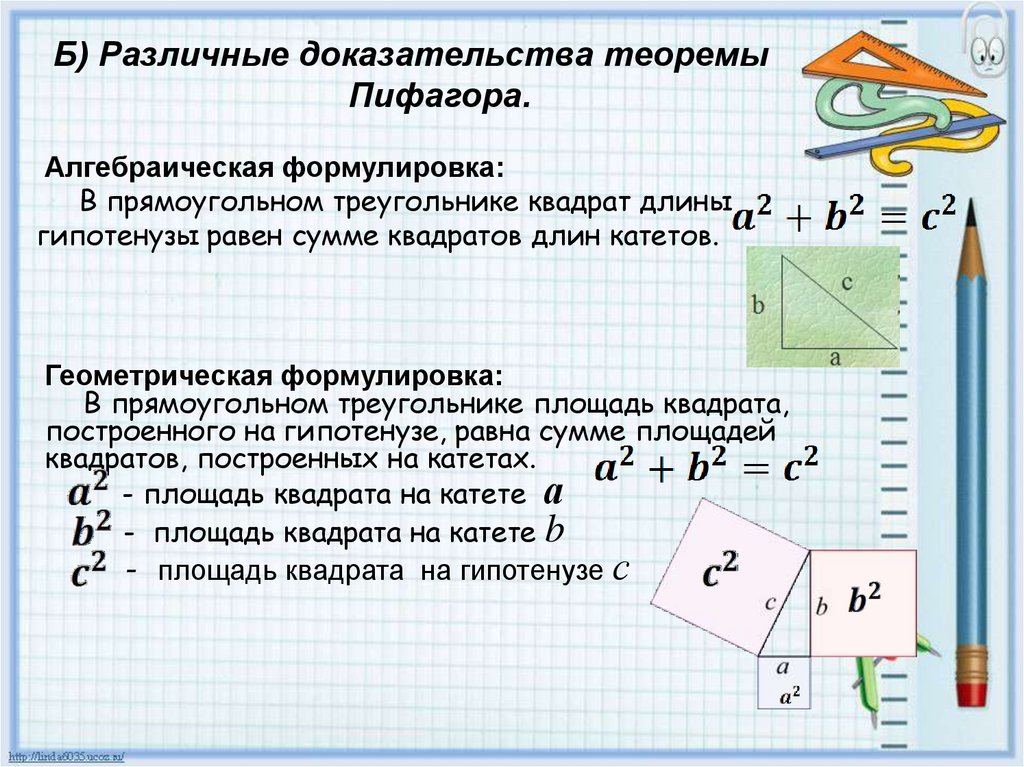
Б) Различные доказательства теоремыПифагора.
Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины
гипотенузы равен сумме квадратов длин катетов.
Геометрическая формулировка:
В прямоугольном треугольнике площадь квадрата,
построенного на гипотенузе, равна сумме площадей
квадратов, построенных на катетах.
- площадь квадрата на катете а
- площадь квадрата на катете b
- площадь квадрата на гипотенузе с
7. Теорема Пифагора: Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Теорема Пифагора и её доказательства.Теорема Пифагора:
Квадрат гипотенузы прямоугольного
треугольника равен сумме квадратов
катетов.
Способ доказательства опирается
на:
Площади
фигур
Подобие
треугольников
Соотношения
в прямоугольном
треугольнике
8. Я рассмотрела самый наглядный способ доказательства теоремы Пифагора, основанный на равенстве площадей фигур.
1.Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов.
(площадь квадрата, построенного на гипотенузе равен сумме площадей квадратов,
построенных на катетах)
Простейшее доказательство теоремы получается в простейшем случае равнобедренного
прямоугольного треугольника. Вероятно, с него и начиналась теорема. Достаточно просто
посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться
в справедливости теоремы. Например: Δ АВС. Квадрат, построенный на гипотенузе АС,
содержит 4 треугольника. А квадраты, построенные на катетах – по 2. Теорема доказана.
9. Наглядные примеры доказательства теоремы Пифагора. Доказательство Бхаскари 1. Четыре треугольника имеют площадь 2ab c2 -
площадь квадрата, построенного на гипотенузе с.(а+b)2- площадь большого квадрата. Площадь большого квадрата равен
сумме площадей четырех треугольников и внутреннего квадрата,
построенного на гипотенузе.
(а+b)2 = c2 +2ab; a2+2ab+b2 = c2 +2ab; a2+b2 = c2.
2.
Сумма площадей частей
квадрата, построенного на
гипотенузе , равна сумме
площадей частей квадратов,
построенных на катетах.
10. Доказательство с помощью равенства площадей.
Мы разбили квадрат,построенный на
гипотенузе, на 9 разных
частей.
На квадраты, построенные на
катетах, накладываем эти
части.
Получаем, что все части
большого квадрата
покрывают квадрат
средний и маленький.
Вывод: площадь квадрата,
построенного на
гипотенузе равна сумме
площадей, построенных
на катетах, т.е.
с2 = a2+b2
11.
Глава 2. Пифагоровы тройкиЗадача Пифагора: найти все прямоугольные треугольники с
целочисленными катетами а,в и целочисленной гипотенузой с .
Частные решения задачи Пифагора были известны в глубокой древности. В
папирусе времён фараона Алинемхета I (около 2000 лет до нашей эры),
хранящемся в Египетском музее в Берлине, мы находим прямоугольный
треугольник с отношениями сторон 3:4:5 (32 + 42 = 52).
Пифагоровы тройки.
(Прямоугольные треугольники с целочисленными сторонами нужны для
решения геометрических задач).
12.
По мнению крупнейшего немецкого историка математики М. Кантора(1829 – 1920 ), в Древнем Египте существовала особая профессия
гарпедонаптов – «натягивателей верёвок», которые во время
торжественной церемонии закладки храмов и пирамид размечали прямые
углы с помощью верёвки, имеющей 12 (=3+4+5) равностоящих узлов.
Способ построения прямого угла гарпедонаптами очевиден из
рисунка. Сегодня прямоугольный треугольник с отношением сторон 3:4:5:
называется египетским. Сохранилась глиняная табличка, пифагоровых
троечек.
13.
3. ЗаключениеТысячи путей ведут к заблуждению, а к истине – только один.
Причина популярности теоремы Пифагора триедина: это простота,
красота, значимость. В самом деле, теорема Пифагора проста, но не
очевидна. Это сочетание двух противоречивых начал и придаёт ей особую
притягательную силу, делает её красивой. Кроме того, теорема Пифагора
имеет огромное значение: она применяется в геометрии, буквально на
каждом шагу. Теорема Пифагора по праву является одной из основных
теорем математики. Значение этой теоремы заключается в том, что при ее
помощи можно вывести большую часть теорем в геометрии. Ценность ее в
современном мире также велика, поскольку теорема Пифагора
применяется во многих отраслях деятельности человека. Например, ее
используют при расположении молниеотводов на крышах зданий, при
производстве окон некоторых архитектурных стилей и даже при
вычислении высоты антенн операторов мобильной связи. И это далеко не
весь перечень практического применения данной теоремы. Вот почему
очень важно знать теорему Пифагора и понимать ее значение.
Целью и задачей проекта были - рассмотреть различные доказательства
теоремы Пифагора и ее применения, узнать о тройках Пифагора.
В работе я рассмотрела различные доказательства: от самых ранних
(древнеиндийского и древнекитайского) до современных, которые даны в
школьных учебниках. Рассмотрела различные применения теоремы
Пифагора. Рассмотрела числа, которые называются «пифагоровыми
тройками».
14.
4. Литература.А.В. Волошинов «Пифагор», Москва «Просвещение», 1993 год.
Г.М. Якушева «Математика», Москва, 1997 год.
З.А. Скопец «Геометрические миниатюры», Москва
«Просвещение», 1990 год.
.













 mathematics
mathematics








