Медианы, биссектрисы и высоты треугольника

1. Медианы, биссектрисы и высоты треугольника

Урок №2

2.

Определения:
1. Медиана треугольника - это…
2. Биссектриса треугольника - это…
3. Высота треугольника - это…

3.

Факты:
B
A
1.
D
2.
A
C
D
если AD =DC ,то…
3.
C
B
если BDC = 900 ,то…
A
A
B
если AKB = CKB ,то…
K
C

4.

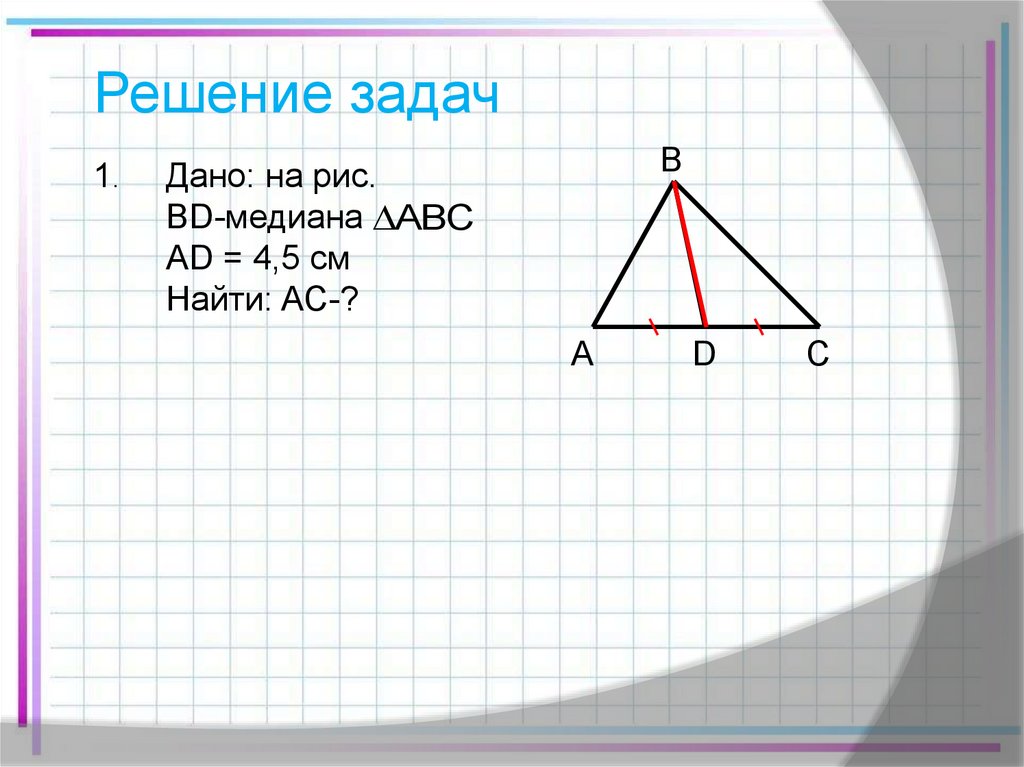
Решение задач
1.
B
Дано: на рис.
BD-медиана ABC
AD = 4,5 см
Найти: AC-?
A
A
D
C

5.

Решение задач
2.
A
Дано: на рис.
BD-высота ABC
Определите:
вид ABD è CBD -?
A
D
B
C

6.

Решение задач
3.
Дано: на рис.
A
KB-биссектриса AKC
AKC = 90
Найти: BKC -?
Назовите: высоты AKC -?
A
K
B
C

7.

Решение задач
Задача №1
Дано: на рис.
BE-медиана ABC
AE=5см
BC=7см
AC BF
Найти: PΔABC -?
B
7см
7см
A 5см E
F
Ответ: PΔABC 24ñì
5см
C

8.

Решение задач
B
Задача №2
Дано: на рис. AB=CB
BD-биссектриса ABC
Докажите: BD-медиана ABC
A
D
C

9.

Решение задач
B
Задача №3
Дано: на рис. AB=CB
BD-биссектриса ABC
Докажите: BD-высота ABC
A
D
C

10.

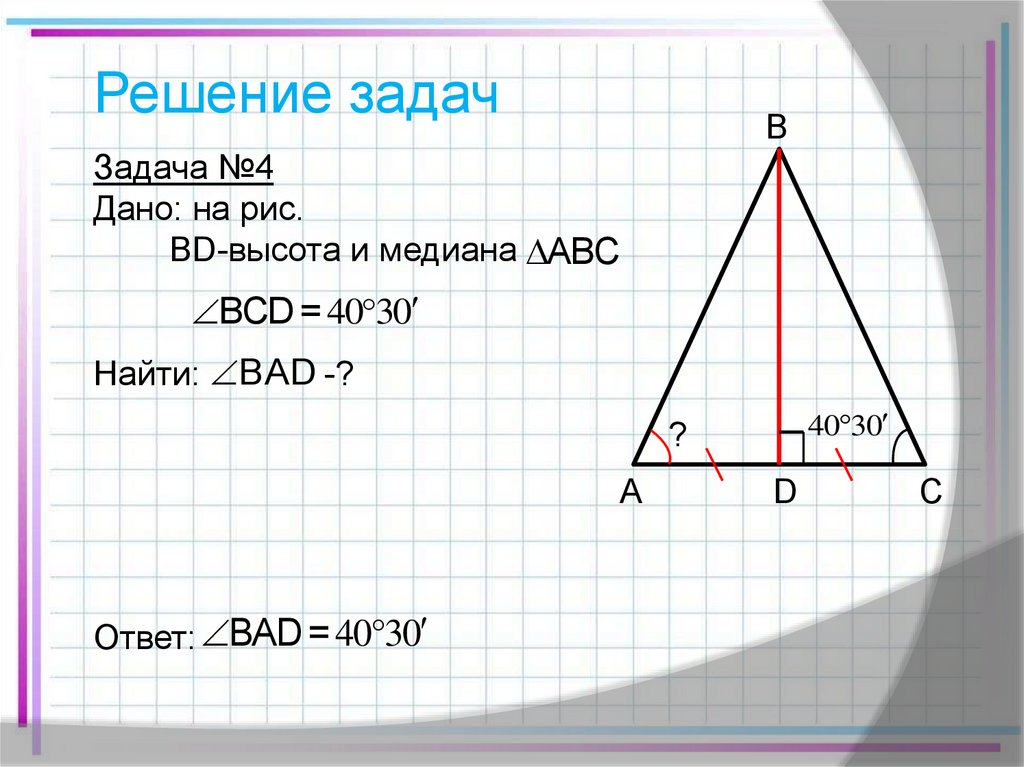
Решение задач
B
Задача №4
Дано: на рис.
BD-высота и медиана ABC
BCD = 40 30
Найти: BAD -?
40 30
?
A
Ответ: BAD = 40°30
D
C

11.

Решение задач
Задача №5
B
C
H
A
D

12.

Решение задач
Задача №1
Дано: на рис.
AO-медиана ABC
AO=OK
AB=6,3см
6,3см
BC=6,5см
AC=6,7см
Найти: CK-?
A
Ответы: а) 6,4см
б) 6,7см
в) 6,5см
г) 6,3см
6,3см
B
K
6,5см
O
6,7см
C

13.

Решение задач
Задача №2
Дано: на рис.
OH-высота MOK
ON-высота EOF
OH=ON
EN=7,8см
OE=8,6см
HM=6,3см
EN=HK
Найти: EK-?
Ответы: а) 13,9см
б) 17,2см
в) 14,9см
г) 16,4см
E 7,8см
N
F
8,6см
O
M
6,3см H
K

14.

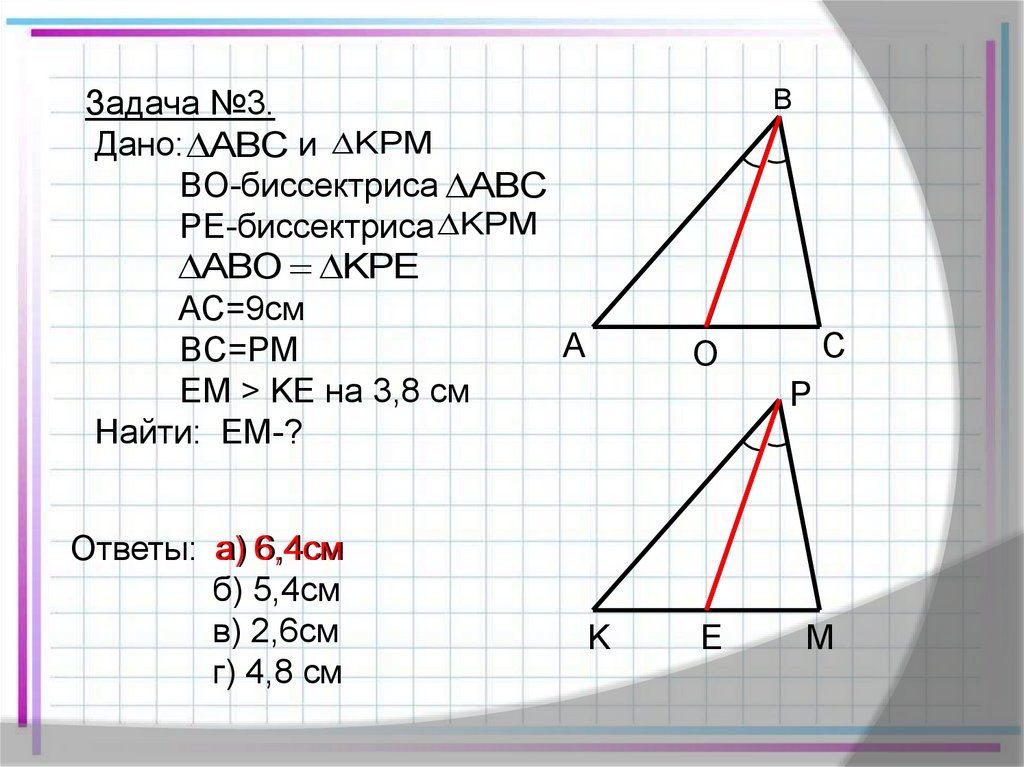
Задача №3.
Дано: ABC и KPM
BO-биссектриса ABC
PE-биссектриса KPM
ABO KPE
AC=9см
A
BC=PM
EM > KE на 3,8 см
Найти: EM-?
Ответы: а) 6,4см
б) 5,4см
в) 2,6см
г) 4,8 см
B
C
O
P
K
E
M

15.

Домашнее задание:
учебник п.17 стр.47-48 вопросы 7,8,9
№106,
рабочая тетрадь № 63-65 стр. 26

16. Спасибо за внимание!

17.

Определения:
1. Отрезок, соединяющий вершину треугольника с
серединой противоположной стороны,
называется медианой треугольника.
2. Отрезок биссектрисы угла треугольника,
соединяющий вершину треугольника с точкой
противоположной стороны, называется
биссектрисой треугольника.
3. Перпендикуляр, проведённый из вершины
треугольника к прямой, содержащей
противоположную сторону, называется высотой
треугольника.