Similar presentations:
Равнобедренный треугольник
1.
12.
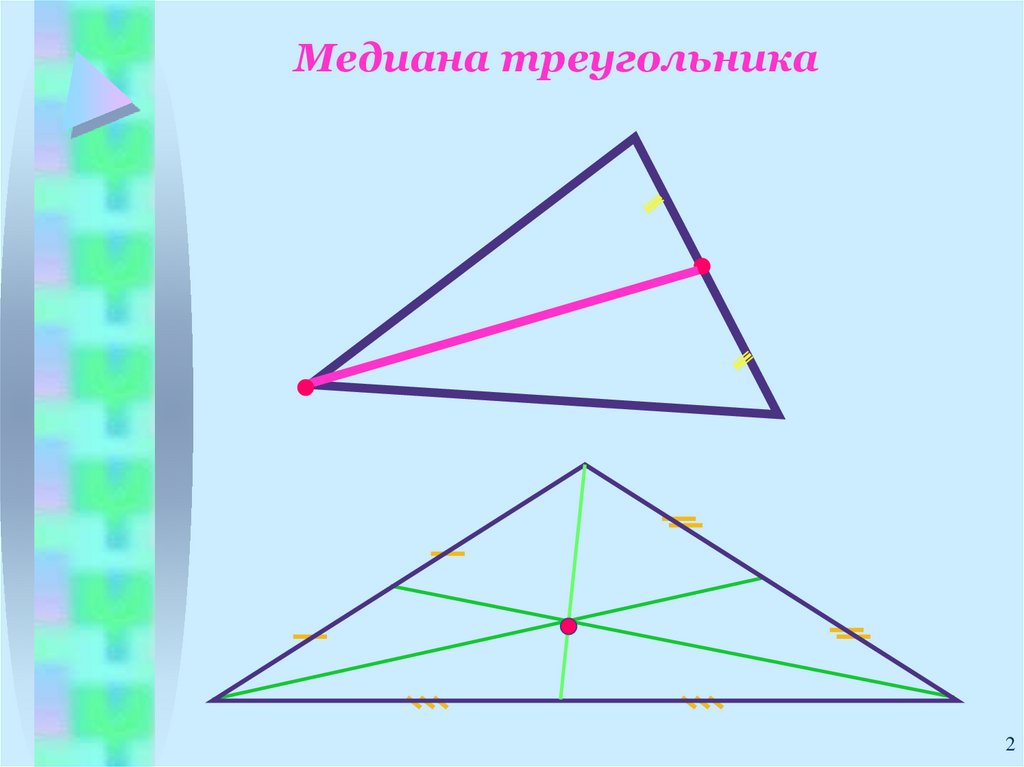
Медиана треугольника2
3.
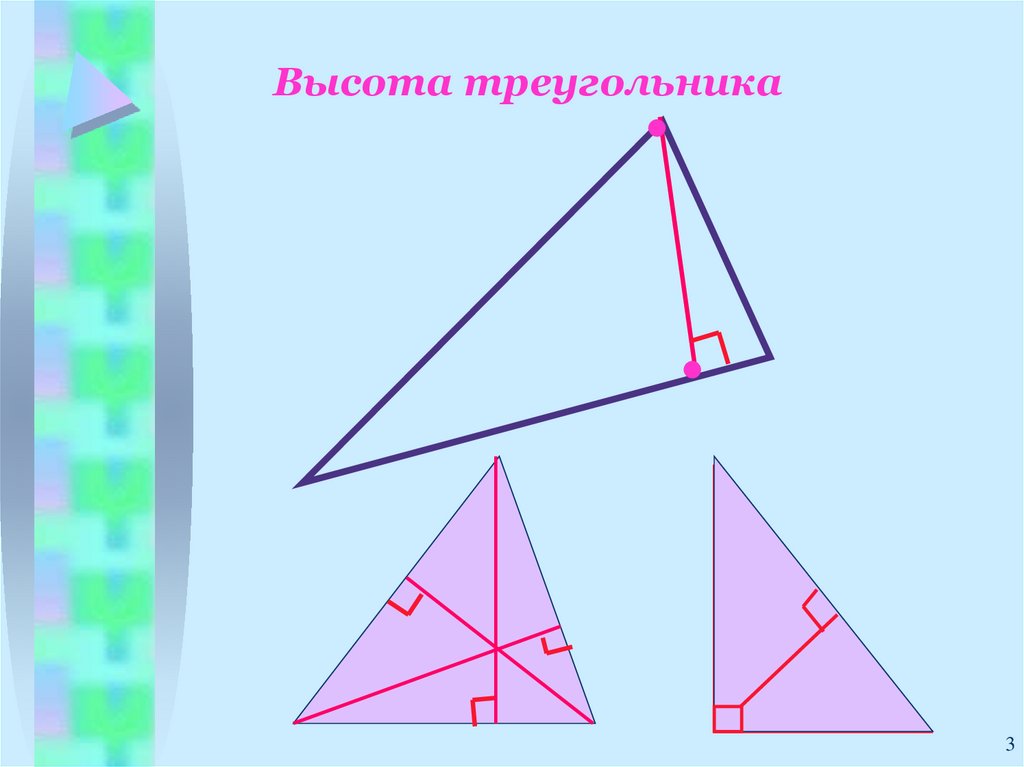
Высота треугольника3
4.
45.
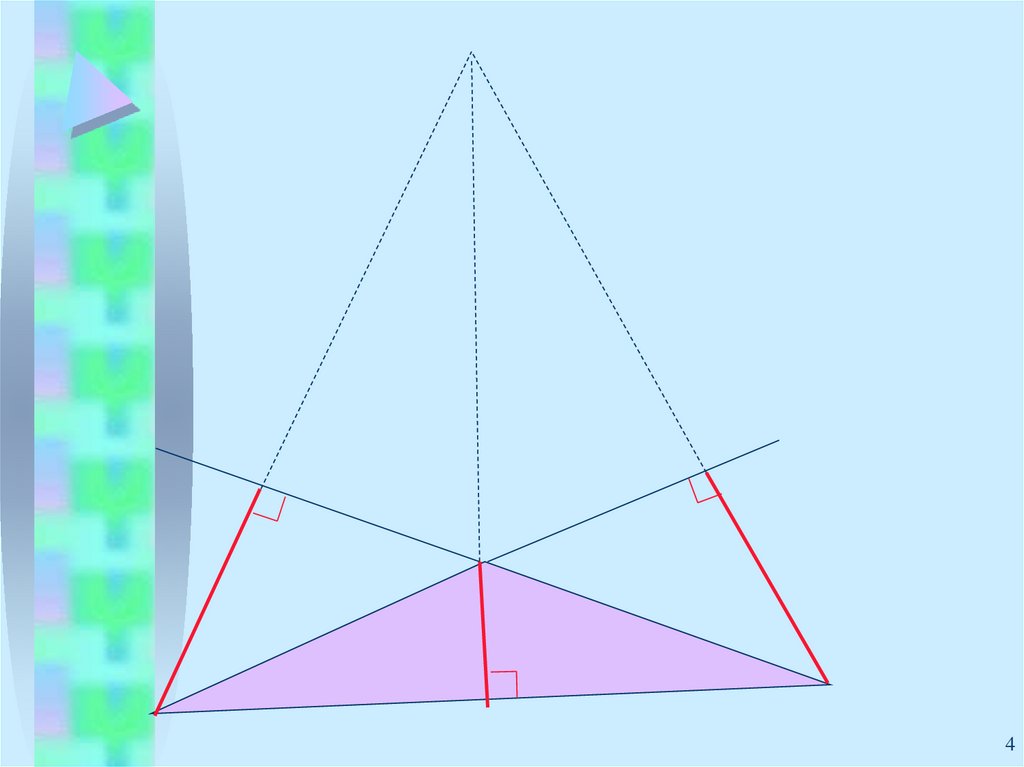
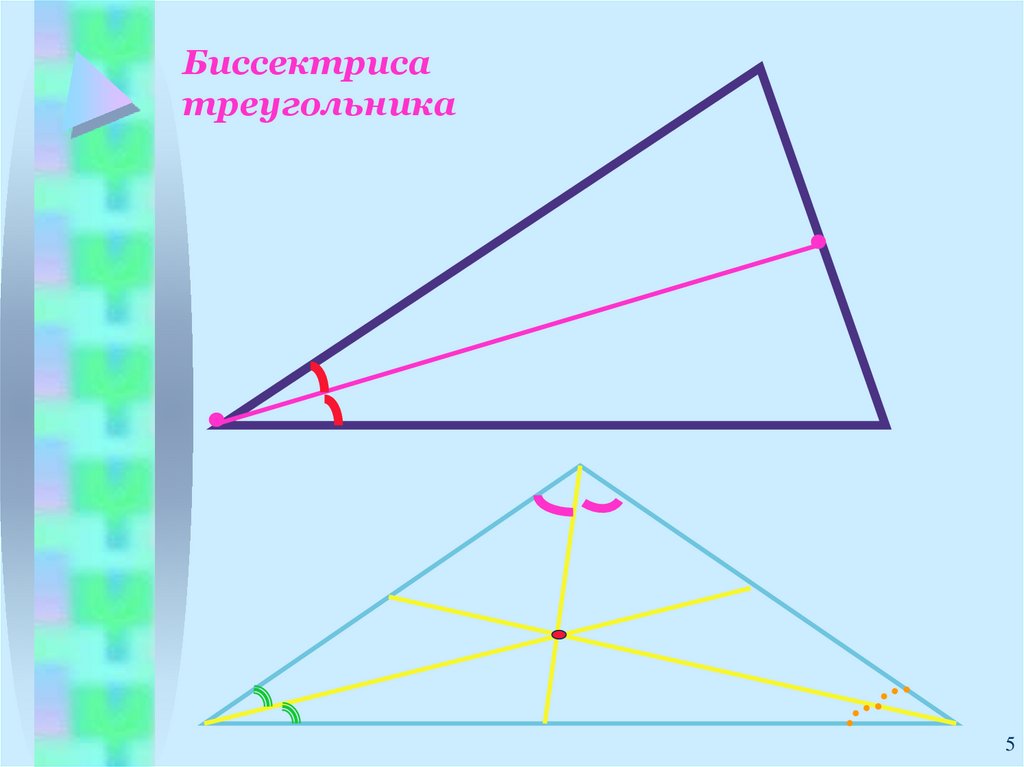
Биссектрисатреугольника
5
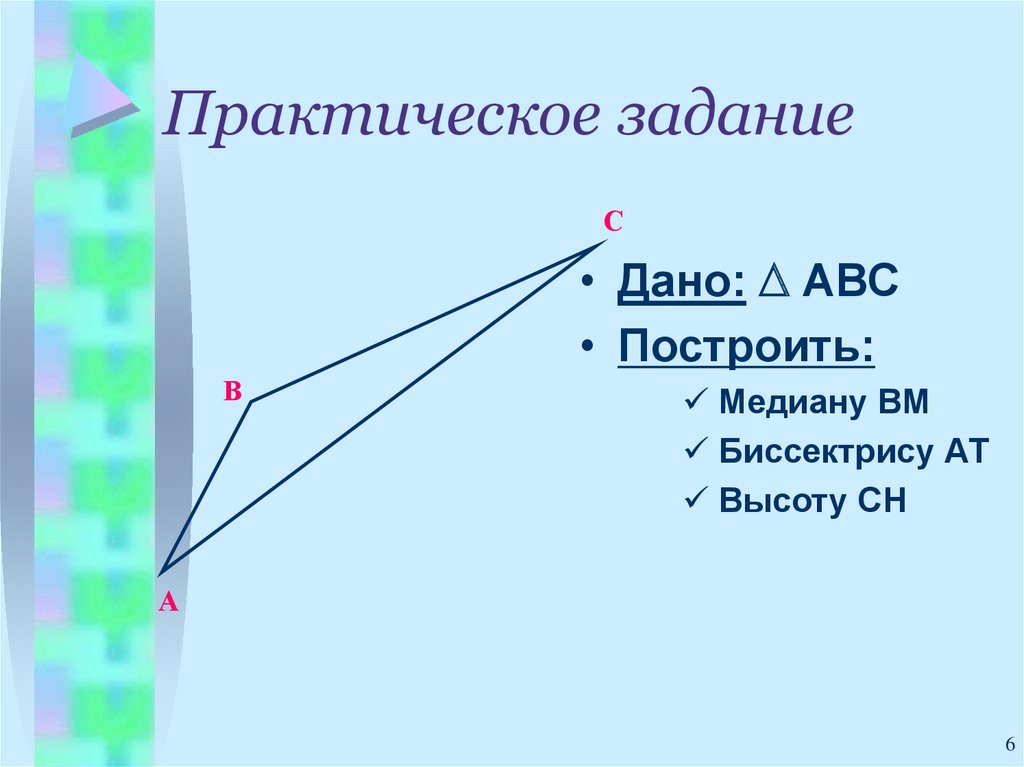
6. Практическое задание
С• Дано: ∆ АВС
• Построить:
В
Медиану ВМ
Биссектрису АТ
Высоту СН
А
6
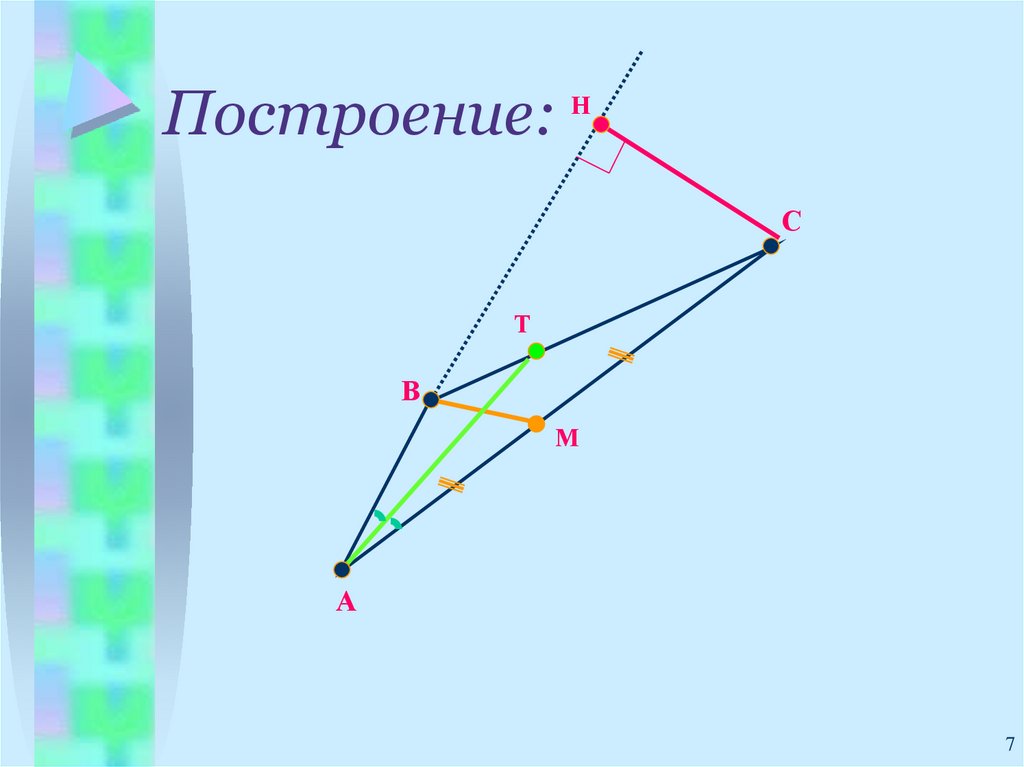
7. Построение:
НС
Т
В
М
А
7
8.
Ни одно человеческое исследование неможет назваться истинной наукой,
если оно не прошло через
математические доказательства
Леонардо да Винчи
8
9.
«Стиохейа»(греческое)-
«Начала»
9
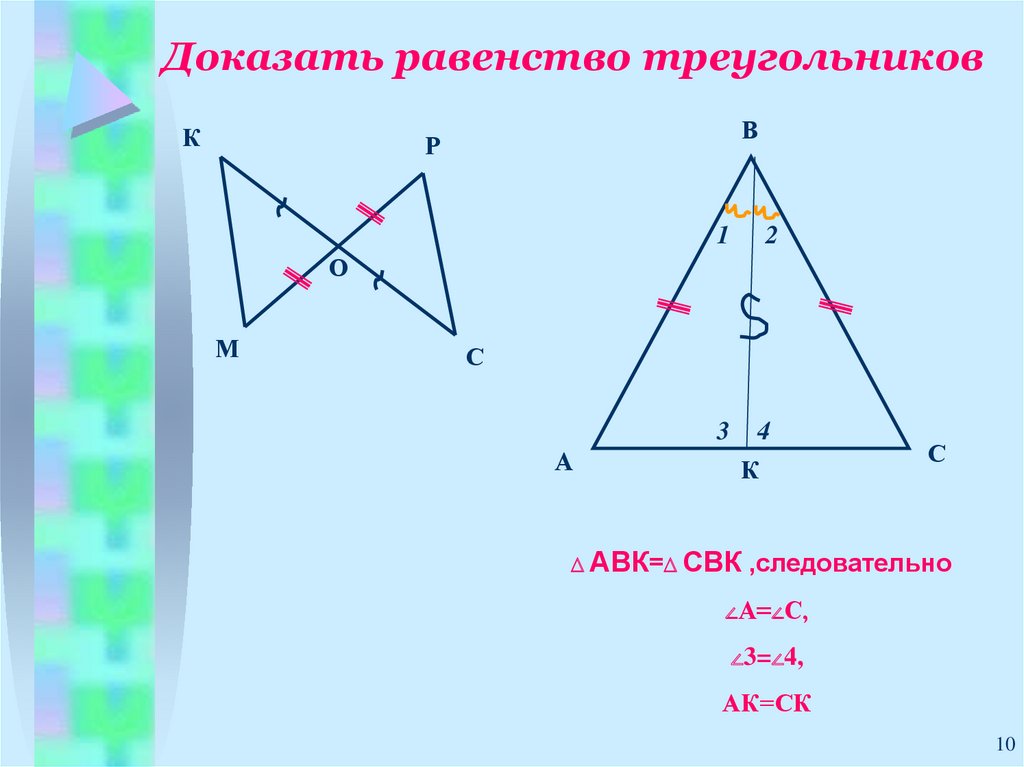
10. Доказать равенство треугольников
КВ
Р
1
2
О
М
С
3
А
4
К
∆ АВК=∆ СВК
С
,следовательно
∠А=∠С,
∠3=∠4,
АК=СК
10
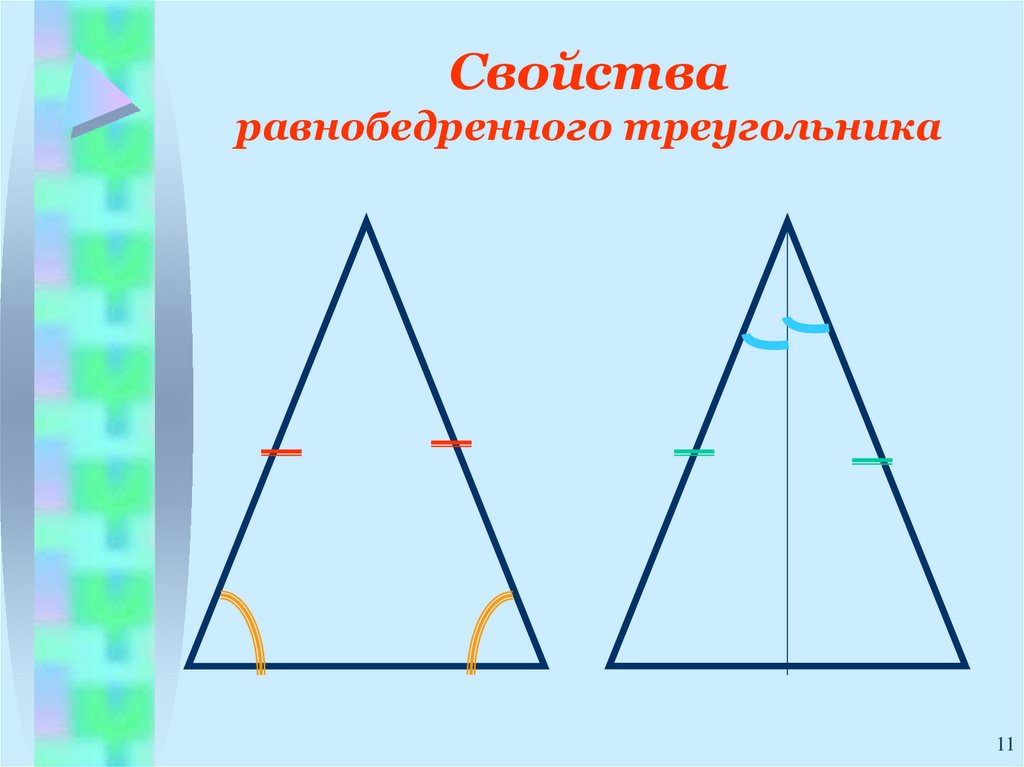
11. Свойства равнобедренного треугольника
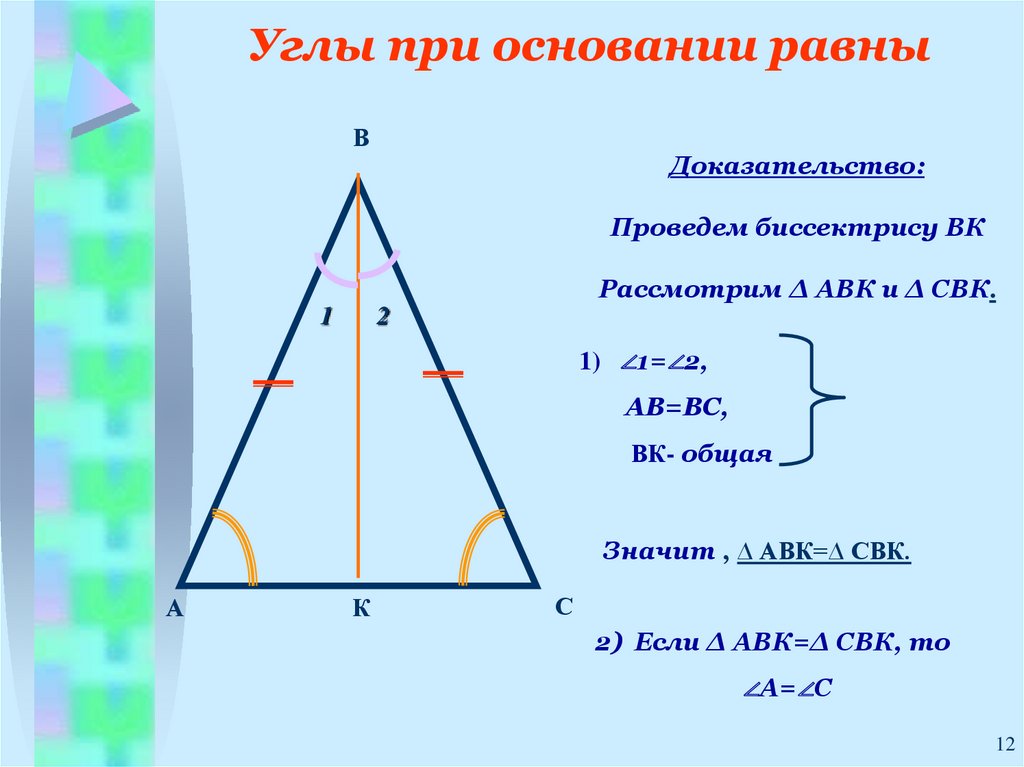
1112. Углы при основании равны
ВДоказательство:
Проведем биссектрису ВК
Рассмотрим ∆ АВК и ∆ СВК.
1
2
1) ∠1=∠2,
АВ=ВС,
ВК- общая
Значит , ∆ АВК=∆ СВК.
А
К
С
2) Если ∆ АВК=∆ СВК, то
∠А=∠С
12
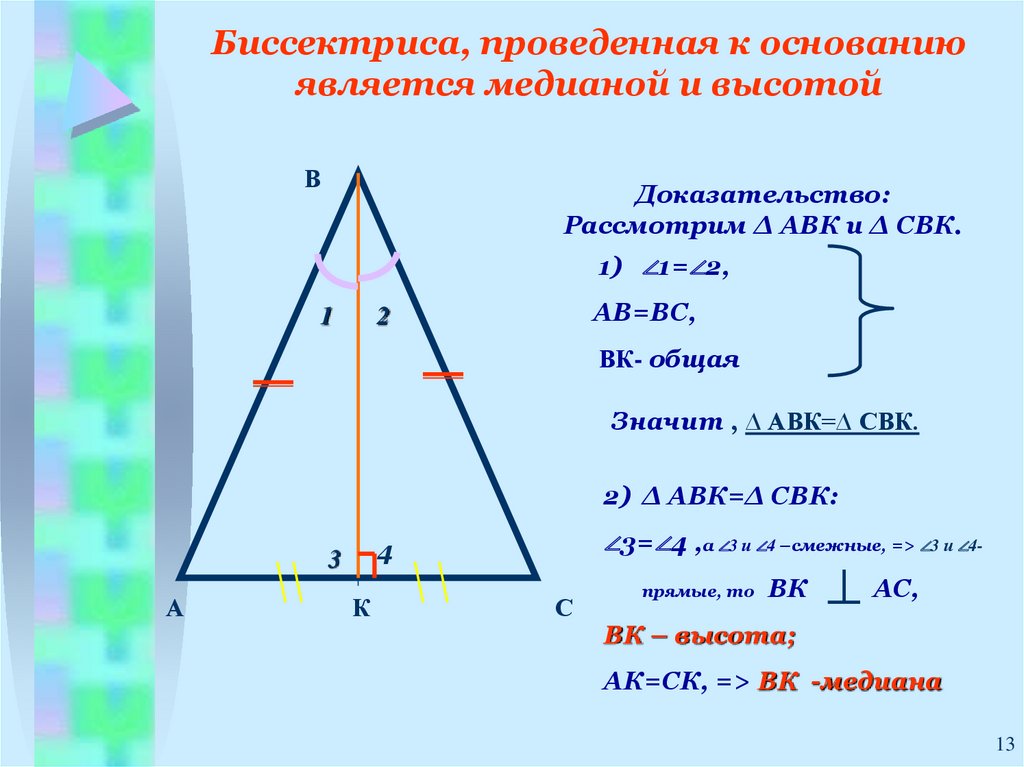
13. Биссектриса, проведенная к основанию является медианой и высотой
ВДоказательство:
Рассмотрим ∆ АВК и ∆ СВК.
1) ∠1=∠2,
1
АВ=ВС,
2
ВК- общая
Значит , ∆ АВК=∆ СВК.
2) ∆ АВК=∆ СВК:
А
∠3=∠4 ,а ∠3 и ∠4 –смежные, => ∠3 и ∠4-
4
3
К
С
прямые, то
ВК
АС,
ВК – высота;
АК=СК, => ВК -медиана
13
14.
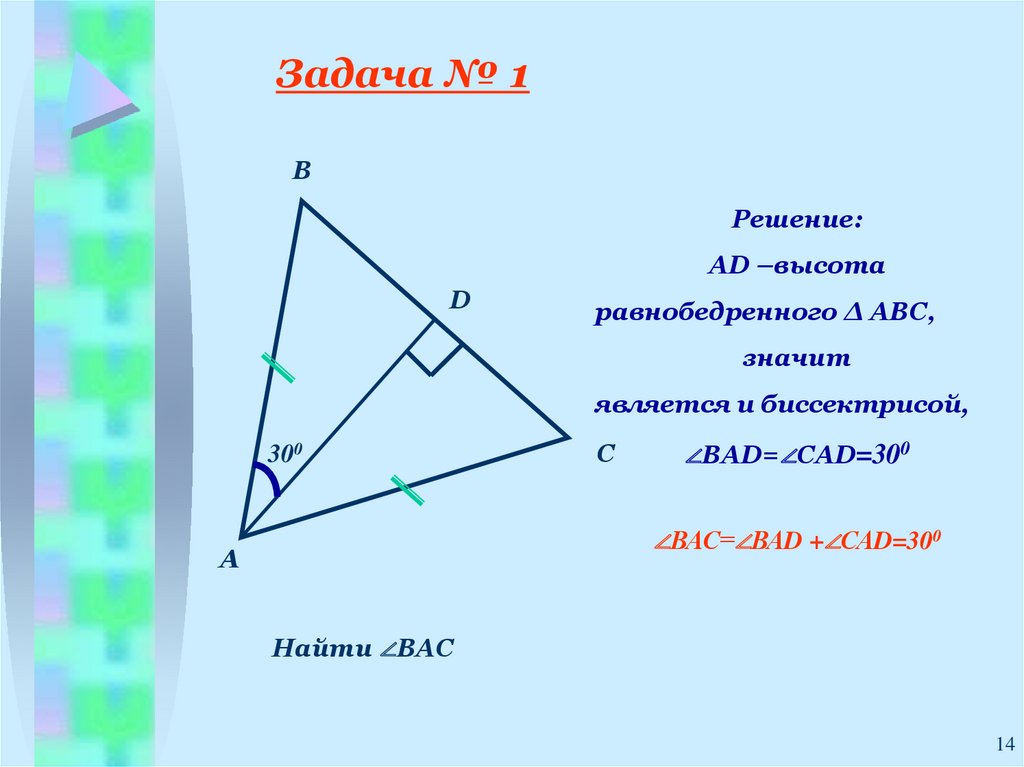
Задача № 1В
Решение:
АD –высота
D
равнобедренного ∆ АВС,
значит
является и биссектрисой,
300
С
∠ВАD=∠САD=300
∠ВАС=∠ВАD +∠САD=300
А
Найти ∠ВАС
14
15.
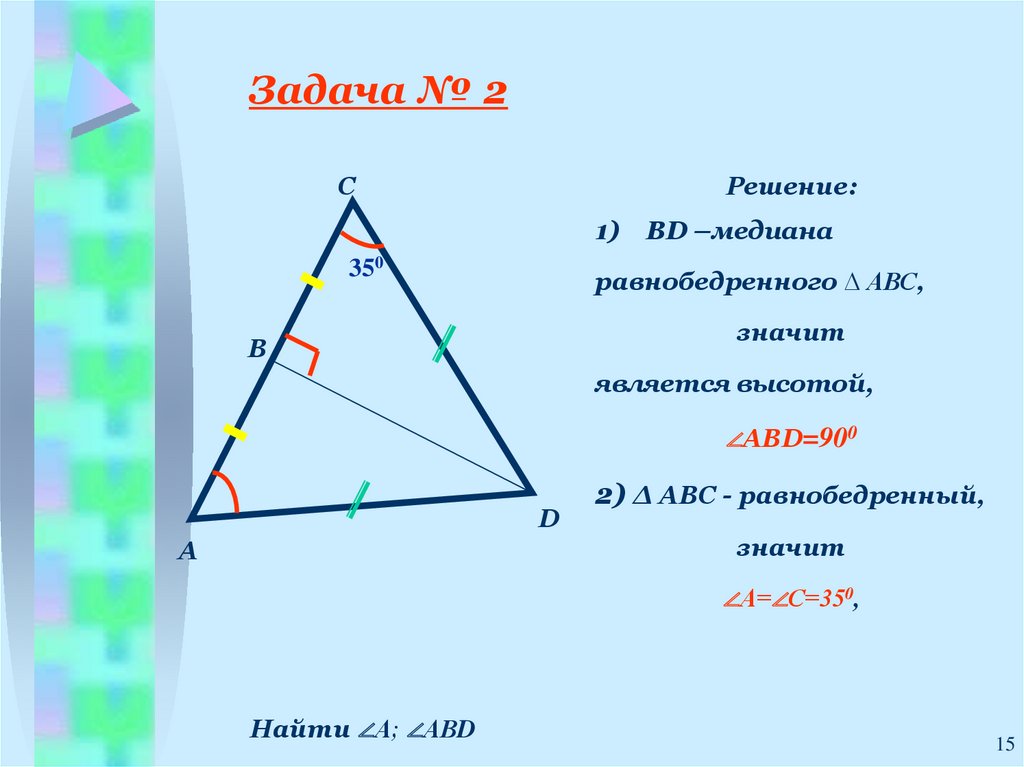
Задача № 2С
Решение:
1)
350
ВD –медиана
равнобедренного ∆ АВС,
значит
В
является высотой,
∠АВD=900
D
А
2) ∆ АВС - равнобедренный,
значит
∠А=∠С=350,
Найти ∠А; ∠АВD
15
16. Домашнее задание на вторник 17 октября
• § 2, п.17-18• №108,112
• Сочинить сказку,
стихотворение
• по теме «Треугольник»
16





 mathematics
mathematics