Задачи из пособия Р. К. Гордина

1. Задачи из пособия Р. К. Гордина

Учитель математики МОУ
СОШ № 5 г Лермонтова
Рудневская Е. Т.

2. п. 1 Медиана прямоугольного треугольника.

1. В прямоугольном треугольнике АВС
гипотенуза АВ равна с и АВС а . Найти все
медианы в этом треугольнике.
C
90
Дано:
Δ
АВС,
, АВ=с,
В
АВС а
a
М
К
С
СМ, АК, ВN - медианы
Найти: СМ, АК, ВN
А
N

3. Решение:

В
a
К
С
М
N
Поскольку медиана прямоугольного треугольника,
проведённая из вершины прямого угла, равна
половине гипотенузы, медиана СМ равна
c
Из треугольника АКС, угол С - прямой
А 2
CK
1
1
1
BC AB cos c cos
2
2
2
По теореме Пифагора из прямоугольного треугольника АСК находим, что
1
AK AC 2 CK 2 ( AB sin ) 2 ( AB cos ) 2
2
c
c
4 sin 2 cos 2
1 3 sin 2
2
2
c
1 3 cos 2
Аналогично находим медиану ВN=
2
Ответ: c ; c 1 3 sin 2 ; c 1 3 cos 2
2
2
2

4. Пример 1. Найти гипотенузу прямоугольного треугольника с острым углом 15⁰ , если известно, что высота треугольника, опущенная

на гипотенузу, равна1.
Дано: Δ АВС, C 90 , А 15
СН - высота , СН=1
В
Найти: АВ
Н
Решение:
М
Проведём медиану СМ. Тогда
СMH 30 как внешний угол
треугольника АМС.
А
Медиана СМ равна половине
С
гипотенузы АВ.
Из прямоугольного треугольника СМН с острым углом 30 ⁰ и
противолежащим ему катетом следует СМ=2СН=2, АВ=2СМ=4
Ответ: АВ=4

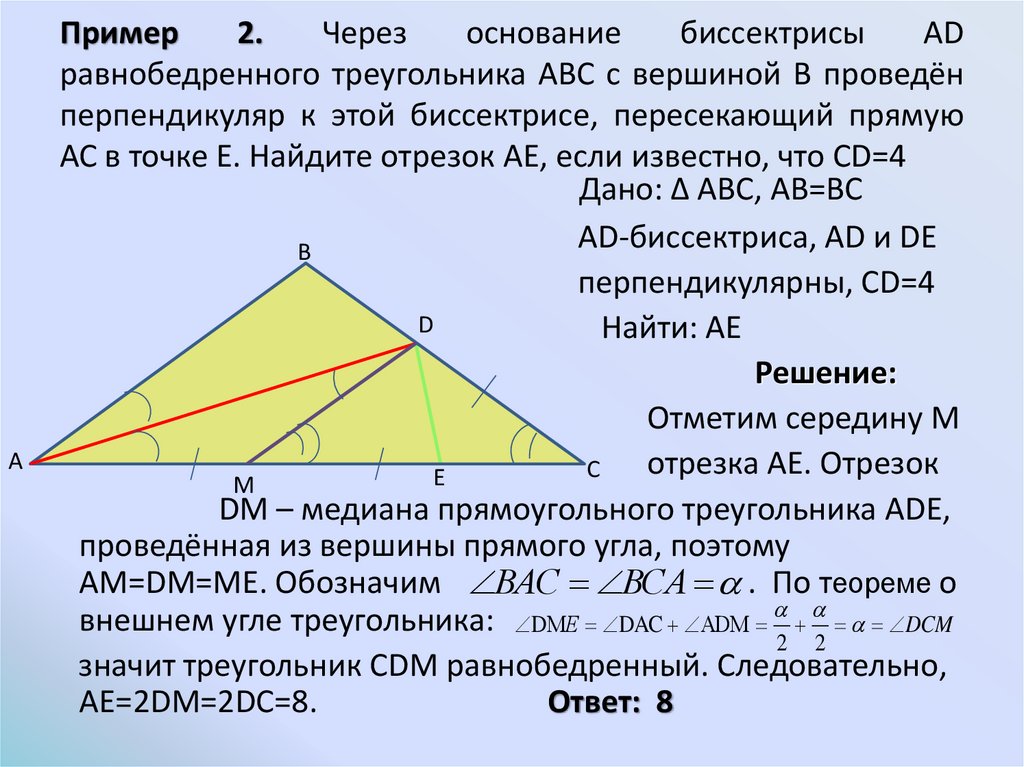
5. Пример 2. Через основание биссектрисы АD равнобедренного треугольника АВС с вершиной В проведён перпендикуляр к этой

А
Пример
2.
Через
основание
биссектрисы
АD
равнобедренного треугольника АВС с вершиной В проведён
перпендикуляр к этой биссектрисе, пересекающий прямую
АС в точке Е. Найдите отрезок АЕ, если известно, что СD=4
Дано: ∆ АВС, АВ=ВС
АD-биссектриса, АD и DЕ
В
перпендикулярны, СD=4
D
Найти: АЕ
Решение:
Отметим середину М
отрезка АЕ. Отрезок
C
Е
М
DМ – медиана прямоугольного треугольника АDЕ,
проведённая из вершины прямого угла, поэтому
АМ=DМ=МЕ. Обозначим ВАС ВСА . По теореме о
внешнем угле треугольника: DМЕ DAC АDМ DCM
2 2
значит треугольник СDМ равнобедренный. Следовательно,
АЕ=2DМ=2DС=8.
Ответ: 8

6. Подготовительные задачи

1.1 Гипотенуза прямоугольного треугольника
равна 4. найдите радиус описанной
окружности.
C
90
Дано: Δ АВС,
В
АВ =4
Найти: R
Решение:
А
С
По условию треугольник прямоугольный,
значит гипотенуза – диаметр описанной
окружности и R=2. Ответ: 2

7. 1.2 Медиана, проведённая к гипотенузе прямоугольного треугольника, равна m и делит прямой угол в отношении 2:1. Найдите стороны

треугольника.