Similar presentations:
Геометрические преобразования графиков функций
1.
Составила: Сизьмина Наталья СергеевнаSillamäe Kannuka Kool
Предмет : математика
Класс: 11 кл.
Работа: Презентация: Геометрические
преобразования графиков функций.
( при технической поддержке ученицы 11 класса)
Используется при объяснении нового материала, на
обобщающем уроке по данной теме, на уроках
повторения в 11 классе и при подготовке
к Г.Э.в 12 классе.
2.
3.
y=-f(x)y=f(-x)
y=f(x)+a
y=f(x+a)
y=a·f(x)
y=f(a·x)
y=|f(x)|
y=f(|x|)
4.
Если известен график функцииy=f(x), то с помощью некоторых
преобразований плоскости
(параллельный перенос, осевая и
центральная симметрии и т. д.)
можно построить графики более
сложных функций:
5.
1)
y=f(x)
График этой функции получается
путём симметричного
отображения графика y=f(x)
относительно оси x.
Замечание: точки пересечения
графика с осью Ox остаются
неизменными.
6.
yy=x2
y
y
y=2x
x
x
x
y=-x2
y=-2x
y
y=sin x
y
x
y=-sin x
7.
2)y=f(x)
График этой функции получается
путём симметричного
отображения графика y=f(x)
относительно оси y.
Замечание: точки пересечения
графика с осью Oy остаются
неизменными.
8.
yy log 2 ( x)
y 2 x
y
y log 2 x
y=2x
-1
1
x
y
y x
y x
x
x
9.
y=f(x)+а этой функции получается так:
График
3).
а) Если а>0 (положительное), то
путем параллельного переноса
графика y=f(x) на расстояние |a| в
положительном направлении оси
Oy (сдвиг вверх).
б) Если а<0 (отрицательное), то путем
параллельного переноса графика
y=f(x) на расстояние |a| в
отрицательном направлении оси
10.
yy=x²+1
y=x²
y x 1
y
1
0
y=x²1,5
y x
y x 2
1
0
x
x
-1,5
-2
y
2
1
0
y=
si
y= n x+
sin
2
y= x+
s in 1
x
x
11.
y=f(x+а)этой функции получается так:
График
4).
а) Если а>0 (положительное), то путем
параллельного переноса графика
y=f(x) на расстояние |a| в
отрицательном направлении оси Oy
(сдвиг влево).
б) Если а<0 (отрицательное), то путем
параллельного переноса графика
y=f(x) на расстояние |a| в
положительном направлении оси
12.
y=x2y
y x 3 y x
y
y x 2
-3
y=(x+3)2
y=(x-2)2
0
2
x
x
y
y sin( x
0
x
y=sin x
)
3
13.
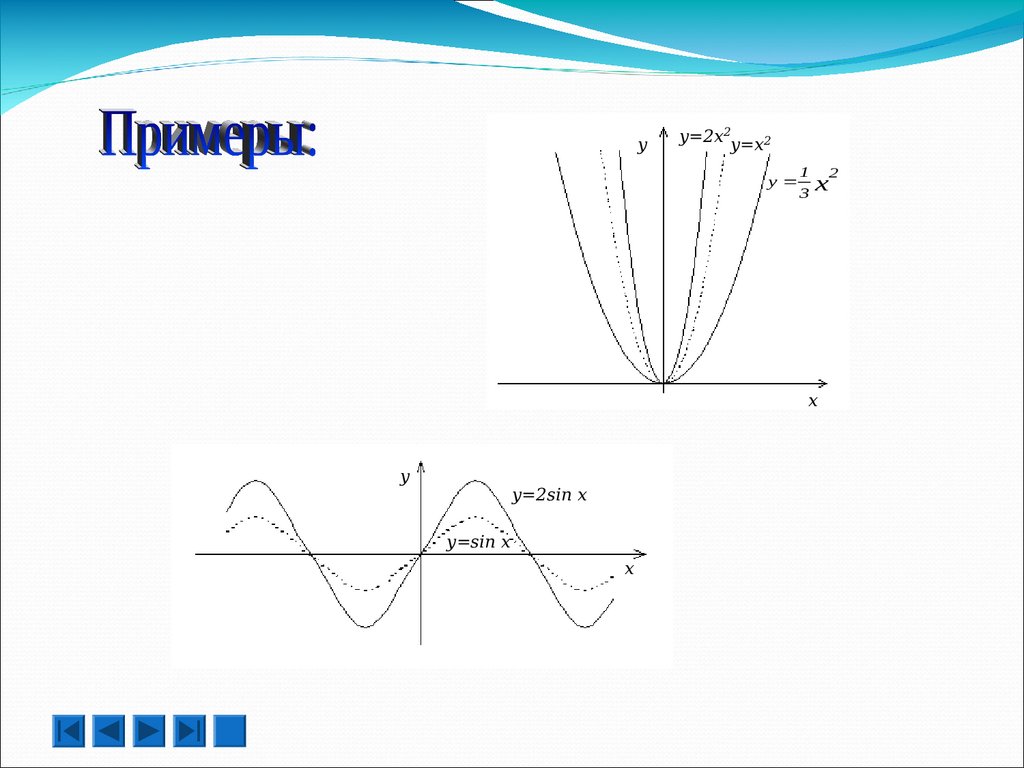
5)y=а·этой
f(x функции получается так:
График
а) Если
а>1, то путём растяжения
)
графика y=f(x) вдоль оси Oy в а раз.
б) Если 0<а<1, то путём сжатия
графика y=f(x) вдоль оси Oy в 1/а раз.
Замечание: точки пересечения
графика с осью Ox остаются
неизменными.
14.
yy=2x2y=x2
y
1
3
x
x
y
y=2sin x
y=sin x
x
2
15.
6).y=f(а·x
График этой функции получается
так:)
а) Если а>1, то путём сжатия
графика y=f(x) вдоль оси Ox в а
раз.
б) Если 0<а<1, то путём
растяжения графика y=f(x) вдоль
оси Ox в 1/а раз.
Замечание: точки пересечения
графика с осью Oy остаются
16.
y 2xy
y x
y x/2
x
y=sin 2x
y
y=sin x
0
2
x
17.
y=|f(x)|
График
этой функции получается так:
7).
Части графика y=f(x), лежащие над
осью Ox и на оси Oy, сохраняются, а
части лежащие ниже оси Ox –
симметрично отображаются
относительно оси Ox («нижнее наверх»).
Замечание: График этой функции
полностью расположен в верхней
полуплоскости.
18.
yy log 2 x
3|
x
y=|x 2
-4x+
y
x
y
y=|sin x|
x
y=sin x
19.
y=f(|x|) этой функции получается так:
График
8).
1)На промежутке x≥0 график исходной
функции y=f(x) сохраняется;
2)На промежутке x<0 полученная часть
графика (правая часть) отображается
симметрично относительно оси Oy
(«правая - налево»).
Замечание: функция y=f(|x|) – чётная
(её график симметричен
относительно оси Oy).
20.
yy log 2 x
y
y=x 2
-4|x|
+
3
x
x
y
y=sin|x|
x
y=sin x
21.
y=-f(x)y=f(-x)
y=f(x)+a
y=f(x+a)
y=a·f(x)
y=f(a·x)
y=|f(x)|
y=f(|x|)
22.
1. Л.Генденштейн, А.П. Ершова, А.С. ЕршоваНаглядный справочник по алгебре и началам анализа с
примерами.





















 mathematics
mathematics








