Similar presentations:
Сумма углов треугольника
1.
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕУЧРЕЖДЕНИЕ ГОРОДСКОГО ОКРУГА БАЛАШИХА
САЛТЫКОВСКАЯ ГИМНАЗИЯ
Автор проекта учитель математики
Сочина Светлана Владимировна
2.
• доказать теорему о сумме угловтреугольника;
• вывести следствие из теоремы –
свойство внешнего угла треугольника;
• научить решать задачи на применение
теоремы.
3.
Дано: АF||ВD,AB= ВF, В = 30°.
C
Доказать: ВD биссектриса СВF.
B
D
300
Найти: А, F,
сумму углов ∆ АВF.
A
F
4.
Доказательство: АF||ВD =>BAF = CBD–соответственные углы;
AFB = FBD – накрест лежащие углы.
AB = BF => ∆ ABF – равнобедренный =>
FAB = AFB (углы при основании
равнобедренного треугольника) =>
CBD = BDF => ВD - биссектриса СВF.
Решение:
ABC = 180° – развернутый угол,
ABF + FBD + DBC = 180° =>
30° + 2 FBD = 180° =>
2 FBD = 180° – 30° = 150° => FBD
= 75° => А = F= 75° .
В ∆ АВF А+ F+ B=30°+ 75°+
75°=180° => сумма углов ∆ АВF
равна 180° .
A
C
B
D
300
F
5.
Дано: DЕ||АС.D
B
E
Найти: сумму углов
∆АВС.
A
C
6.
Решение:DЕ||АС => DBA = BAC,
ACB = CBE – накрест
лежащие углы.
DBE
=
180°
–
развернутый
угол
=>
DBA + ABC + CBE =
180°
В ∆АВС
A + B + C = 180° =>
сумма углов в ∆АВС равна
180°.
D
A
B
E
C
7.
(365 — около 300 гг. до н. э)древнегреческий
математик.
Работал в Александрии в 3 в. до
н. э. Главный труд «Начала»,
содержащий основы античной
математики,
элементарной
геометрии, теории чисел, общей
теории отношений и метода
определения
площадей
и
объемов, включавшего элементы
теории пределов, оказал огромное влияние на развитие
математики. Работы по астрономии, оптике, теории
музыки.
8.
Евклид жил в Александрии.Из дошедших до нас сочинений Евклида
наиболее знамениты «Начала», состоящие из 15
книг. В 1-й книге формулируются исходные
положения геометрии,
а также содержатся
основополагающие
теоремы планиметрии,
среди которых теорема
о
сумме
углов
треугольника и теорема
Пифагора.
9.
BA + B + C = 180°
A
C
10.
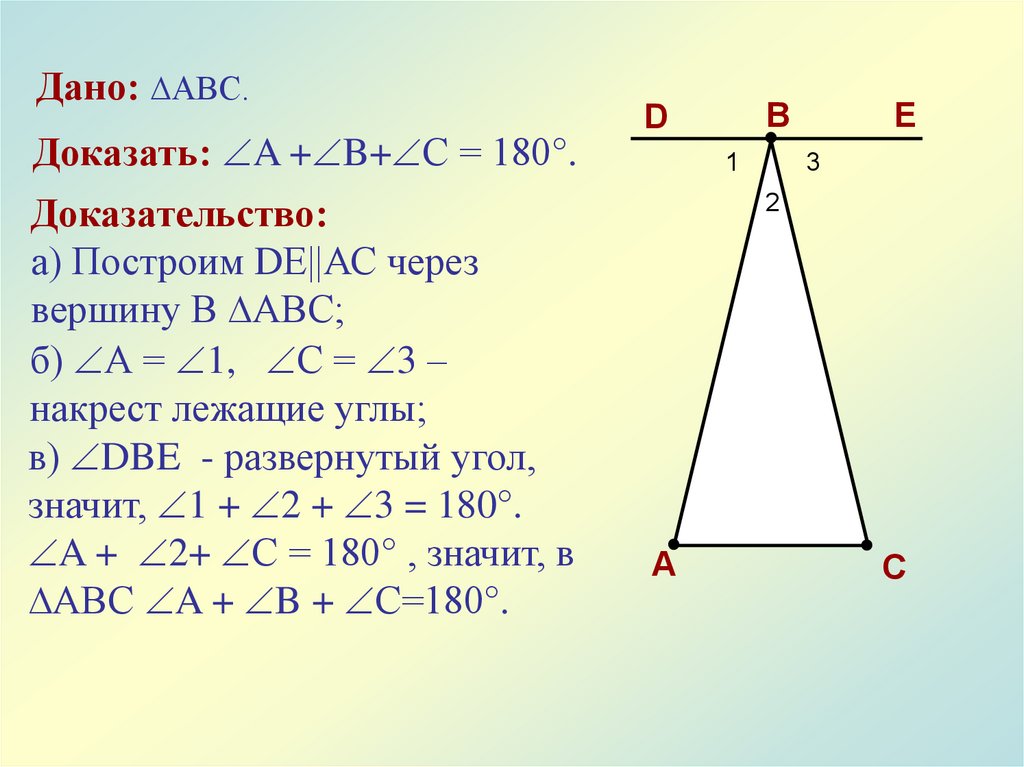
Дано: ∆АВС.Доказать: A + B+ С = 180°.
Доказательство:
а) Построим DЕ||АС через
вершину В ∆АВС;
б) А = 1, С = 3 –
накрест лежащие углы;
в) DBE - развернутый угол,
значит, 1 + 2 + 3 = 180°.
A + 2+ С = 180° , значит, в
∆АВС A + B + С=180°.
B
D
1
E
3
2
A
C
11.
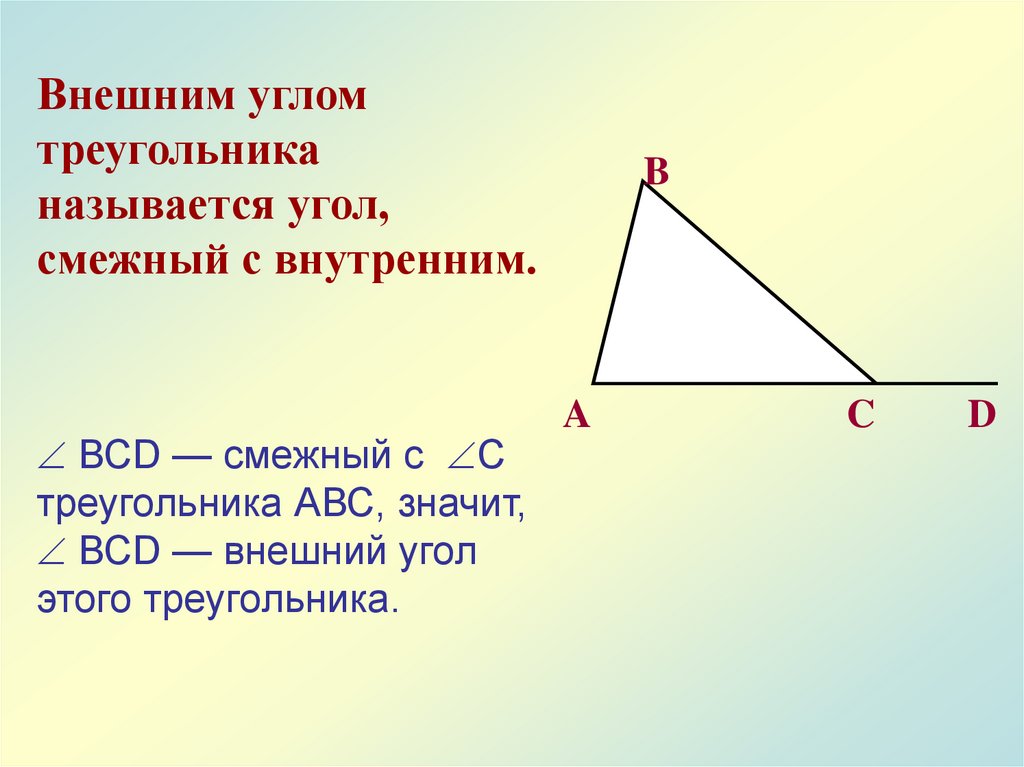
Внешним угломтреугольника
называется угол,
смежный с внутренним.
ВСD — смежный с С
треугольника АВС, значит,
ВСD — внешний угол
этого треугольника.
B
A
C
D
12.
BA
C
D
Внешний угол треугольника равен
сумме двух углов треугольника, не
смежных с ним.
13.
BДано: ∆АВС, ВСD внешний угол ∆АВС.
Доказать: ВСD = А + В.
A
C
Доказательство:
АСВ и ВСD – смежные углы АСВ + ВСD =
180° , значит , ВСD = 180° – АСВ.
Но так как А + В + АСВ = 180° в ∆АВС, то
А + В = 180° – ACB => 180° – ACB = ВСD
=> ВСD = А + В.
D
14.
Решение задач.1. Найдите угол С треугольника
АВС, если:
а) А=65°, В=57°;
б) А=24°, В=1ЗО°;
в) А=α, В=2α.
А
В
С
15.
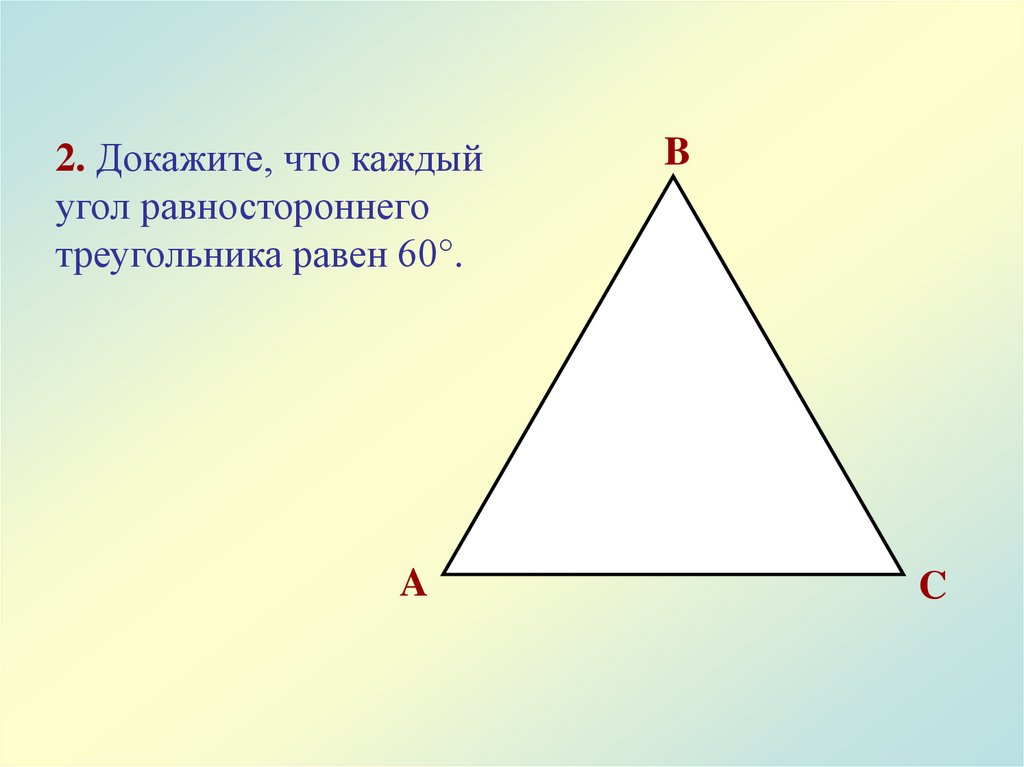
2. Докажите, что каждыйугол равностороннего
треугольника равен 60°.
A
B
C
16.
3. В равнобедренном треугольнике АВС с основаниемАС проведена биссектриса АD. Найдите АDС,
если С=50°.
Домашнее задание.
П. 30, ответить на вопросы на странице 89.
Решить задачи №224, 228(а), 230.
17.
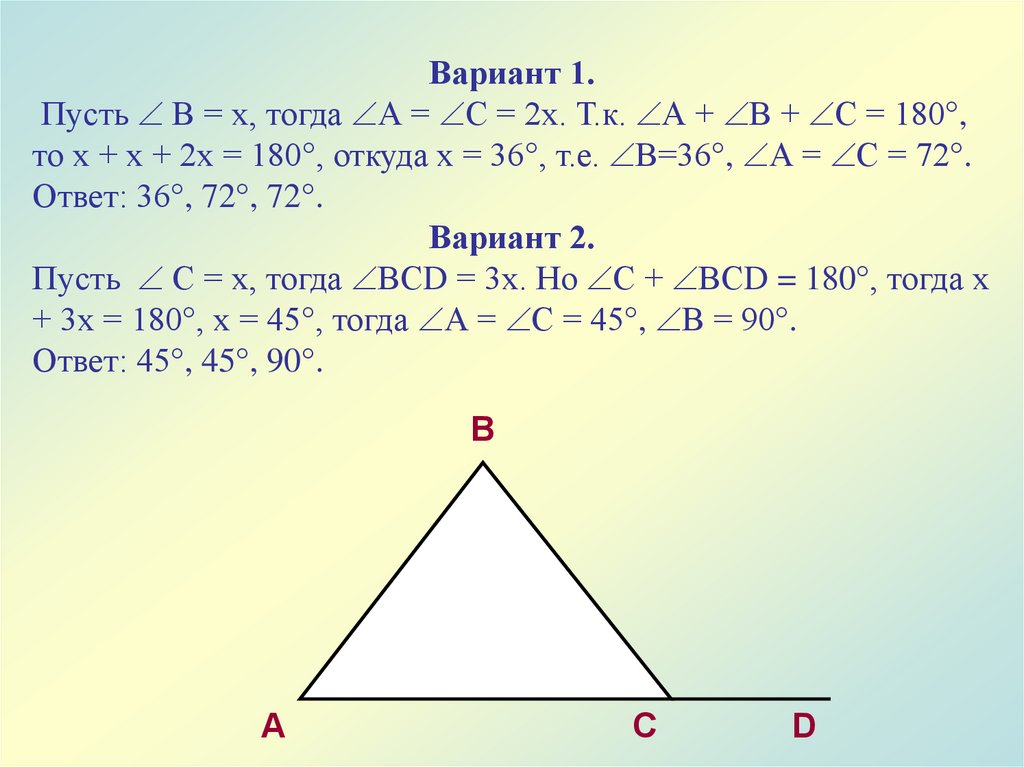
Самостоятельная работа.Вариант 1.
Вариант 2.
Найдите
углы
равнобедренного
треугольника,
если
угол при основании в
два раза больше угла,
противолежащего
основанию.
Найдите углы
равнобедренного
треугольника, если
угол при основании в
три раза меньше
внешнего
угла,
смежного с ним.
18.
Вариант 1.Пусть В = х, тогда А = С = 2х. Т.к. А + В + С = 180°,
то х + х + 2х = 180°, откуда х = 36°, т.е. В=36°, А = С = 72°.
Ответ: 36°, 72°, 72°.
Вариант 2.
Пусть С = х, тогда ВСD = 3х. Но С + ВСD = 180°, тогда х
+ 3х = 180°, х = 45°, тогда А = С = 45°, В = 90°.
Ответ: 45°, 45°, 90°.
B
A
C
D














 mathematics
mathematics








