603.29K

Category: $mathematics$ mathematics

Сумма углов треугольника. Внешние углы

1.

Тема урока: Сумма углов
треугольника. Внешние
углы
Геометрия 7 класс
разработала: Платонова Надежда Владимировна

2.

- Начнем наш урок! Приготовили
тетради, учебники, ручки, карандаши
линейки и транспортиры!
- И в начале урока вспомним, что
было изучено ранее!
К уроку готов!

3.

Вспомним!
Выберите верный ответ:
Две прямые на плоскости называются
параллельными, если они …
Имеют одну
общую точку
Имеют две и
более общих
точек
Не имеют общих
точек

4.

Вспомним!
Две прямые на плоскости называются
параллельными, если они …
- Неверно, попробуй
еще раз
Вернуться!!!

5.

Вспомним!
Две прямые на плоскости называются
параллельными, если они не имеют
общих точек
a
b
- Молодец!!!
Далее

6.

Вспомним!
Выберите верный ответ:
Если при пересечении двух прямых
секущей накрест лежащие углы …, то
прямые параллельны
Равны
Не равны

7.

Вспомним!
Если при пересечении двух прямых
секущей накрест лежащие углы …, то
прямые параллельны
- Неверно, попробуй
еще раз
Вернуться!!!

8.

Вспомним!
Если при пересечении двух прямых
секущей накрест лежащие углы
равны, то прямые параллельны
a
1
2
b
- Молодец!!!
1=
2
Далее

9.

Вспомним!
Выберите верный ответ:
Если две параллельные прямые
пересечены третьей, то сумма
внутренних односторонних углов
равна …
180°
90°
360°

10.

Вспомним!
Если две параллельные прямые
пересечены третьей, то сумма
внутренних односторонних углов
равна …
- Неверно, попробуй
еще раз
Вернуться!!!

11.

Вспомним!
Если две параллельные прямые
пересечены третьей, то сумма
внутренних односторонних углов
равна …
a
1
2
b
- Молодец!!!
1+
2=180°
Далее

12.

Вспомним!
Выберите верный ответ:
Два угла называются … , если у них
одна сторона общая, а другие стороны
этих углов являются
дополнительными полупрямыми.
соответственными
смежными
вертикальными

13.

Вспомним!
Два угла называются … , если у них
одна сторона общая, а другие стороны
этих углов являются
дополнительными полупрямыми.
- Неверно, попробуй
еще раз
Вернуться!!!

14.

Вспомним!
Два угла называются смежными , если
у них одна сторона общая, а другие
стороны этих углов являются
дополнительными полупрямыми.
Далее

15.

Вспомним!
Выберите верный ответ:
Сумма смежных углов равна …
180°
90°
360°

16.

Вспомним!
Сумма смежных углов равна …
- Неверно, попробуй
еще раз
Вернуться!!!

17.

Вспомним!
Сумма смежных углов равна 180°
1
1+
2
2=180°
- Молодец!!!
Далее

18.

- Готов к получению
новых знаний!!!
Вперед

Узнаем новое!
Тема урока: Сумма углов треугольника.
Внешние углы
-Проведем эксперимент:
-В своих тетрадях нарисуйте
три произвольных треугольника:
остроугольный, прямоугольный и
тупоугольный.
Нужна подсказка
Готово!

20.

Подсказка!
Вернуться к заданию

21.

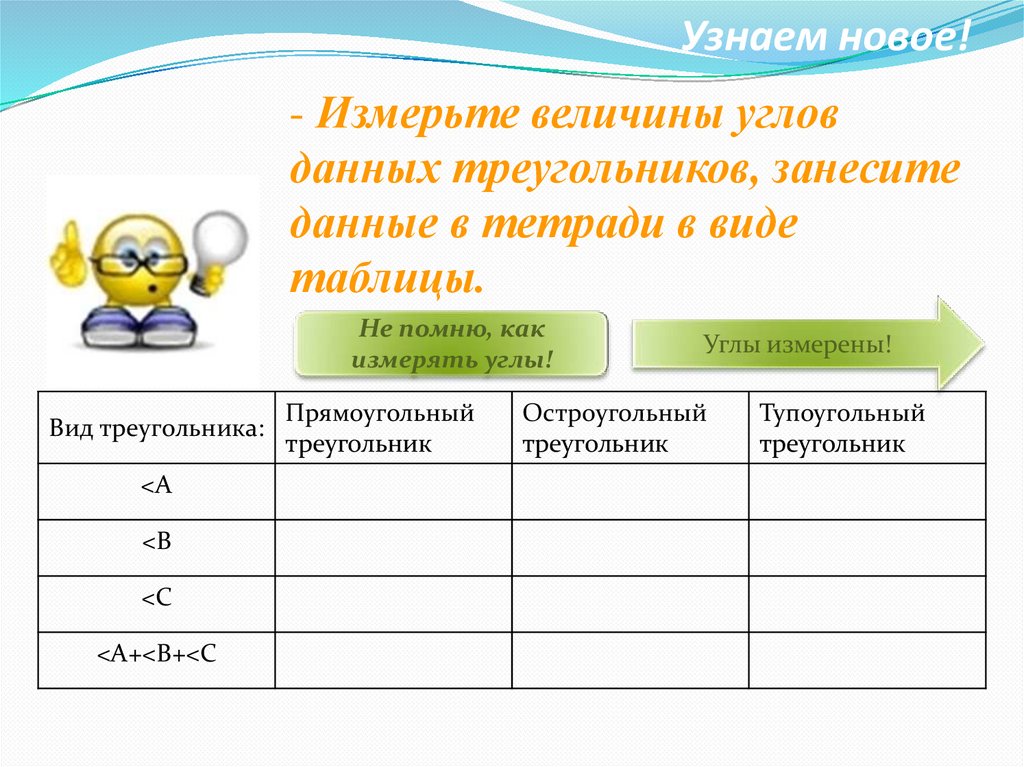
Узнаем новое!
- Измерьте величины углов
данных треугольников, занесите
данные в тетради в виде
таблицы.
Не помню, как
измерять углы!
Вид треугольника:
<A
<B
<C
<A+<B+<C
Прямоугольный
треугольник
Углы измерены!
Остроугольный
треугольник
Тупоугольный
треугольник

22.

Как измерить угол!
<E=47°
Вспомнил, вернуться к
заданию!

23.

Узнаем новое!
- Найдите сумму углов.
Заполните таблицу.
Сравните сумму углов каждого
треугольника.
Далее
Вид треугольника:
<A
<B
<C
<A+<B+<C
Прямоугольный
треугольник
Остроугольный
треугольник
Тупоугольный
треугольник

24.

Узнаем новое!
- Всегда ли сумма углов любого
треугольника равна 180°?
Докажем данный факт!
Вперед к
доказательству

25.

Узнаем новое!
Теорема: Сумма углов треугольника
равна 180°
(данную формулировку и краткое доказательство необходимо записывать в тетрадь)
В
Дано: треугольник ABC
Доказать:
<A+<B+<C=180°
А
С
Доказательство: проведем прямую BD параллельную АС
Прямая BD

26.

27.

Узнаем новое!
Теорема: Сумма углов треугольника
равна 180°
(данную формулировку и краткое доказательство необходимо записывать в тетрадь)
В
D
Дано: треугольник ABC
Доказать:
<A+<B+<C=180°
А
С
Доказательство: проведем прямую BD параллельную АС,
Углы DBC и ACB равны как внутренние накрест лежащие,
при BD||AC и секущей ВС, сумма углов треугольника при
вершинах В и С равна углу ABD
Далее

28.

29.

Закрепим!
Найдите неизвестный угол треугольника:
25°
75°
Проверка

30.

Закрепим!
Найдите неизвестный угол треугольника:
25°
75°
<A+<B+<C=180°
180°-(25°+75°)=80°
Ответ 80°
Далее

31.

Закрепим!
Самостоятельно в тетрадях:
№ 18(1) учебник стр.52
Вернуться
Далее

32.

Подумаем:
Может ли в треугольнике быть
-два тупых угла
-тупой и прямой углы
-два прямых угла?
Следствие 1:
У любого треугольника хотя бы два
угла острые!
Далее

33.

Подумаем:
Чему равны углы равностороннего
треугольника?
Следствие 2:
Угол равностороннего
треугольника равен 60°
Далее

34.

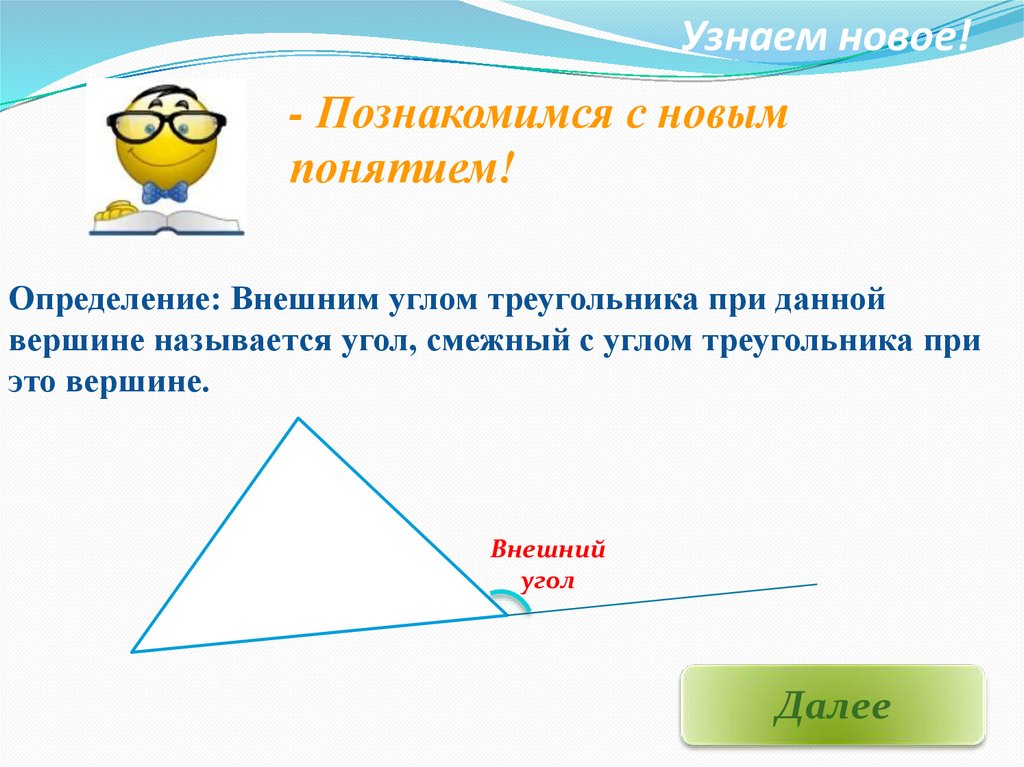
Узнаем новое!
- Познакомимся с новым
понятием!
Определение: Внешним углом треугольника при данной
вершине называется угол, смежный с углом треугольника при
это вершине.
Внешний
угол
Далее

35.

Узнаем новое!
- Изучим теорему и следствие из нее,
доказательство проведем
самостоятельно, если возникнут
проблемы обратимся за помощью к
учебнику страница 47
Теорема: Внешний угол треугольника равен сумме
двух других внутренних углов, не смежных с ним.
Следствие: Внешний угол треугольника больше
любого внутреннего угла не смежного с ним
Выполнено!

36.

Закрепим!
Один из внешних углов равнобедренного
треугольника равен 50°. Найдите остальные углы.
- Пробуем решить самостоятельно, не
получается, пользуемся подсказкой!
Подсказка
Далее

37.

Закрепим!
Один из внешних углов равнобедренного
треугольника равен 50°. Найдите остальные углы.
Угол треугольника, смежный с данным внешним
углом равен 180°- 50°=130°. Так как треугольник
равнобедренный, делаем вывод, что данный угол
находится при вершине.
Следовательно сумма двух других углов равна 50°. Так как
это углы равны, получаем, что каждый из них равен
50°:2=25°.
Ответ: 130°, 25°, 25°
Далее