Решение треугольников. Типы задач на решение треугольников

1.

2. Решение треугольников

Смысл задачи
Типы задач на решение треугольников
Справочные материалы
Основные задачи на решение
треугольников

3. СМЫСЛ ЗАДАЧИ

• Решением треугольника называется
нахождение всех его шести элементов
(т.е. трех сторон и трех углов) по
каким –нибудь трем данным элементам,
определяющим треугольник.

4. ТИПЫ ЗАДАЧ

• Решение треугольника по двум
сторонам и углу между ними.
• Решение треугольника по стороне и
двум прилежащим к ней углам.
• Решение треугольника по трем
сторонам.

5.

Решение прямоугольных
треугольников:

6.

Теорема Пифагора
В прямоугольном
треугольнике квадрат
гипотенузы равен сумме
квадратов катетов
Тригонометрические соотношения
в прямоугольном треугольнике
А
А
в
с
С
а
с
в
B
С
а 2 + в2 = с2
а
B
sin A = a : с
cos A = b : с
tg A = a : в
ctg A = в : а

7.

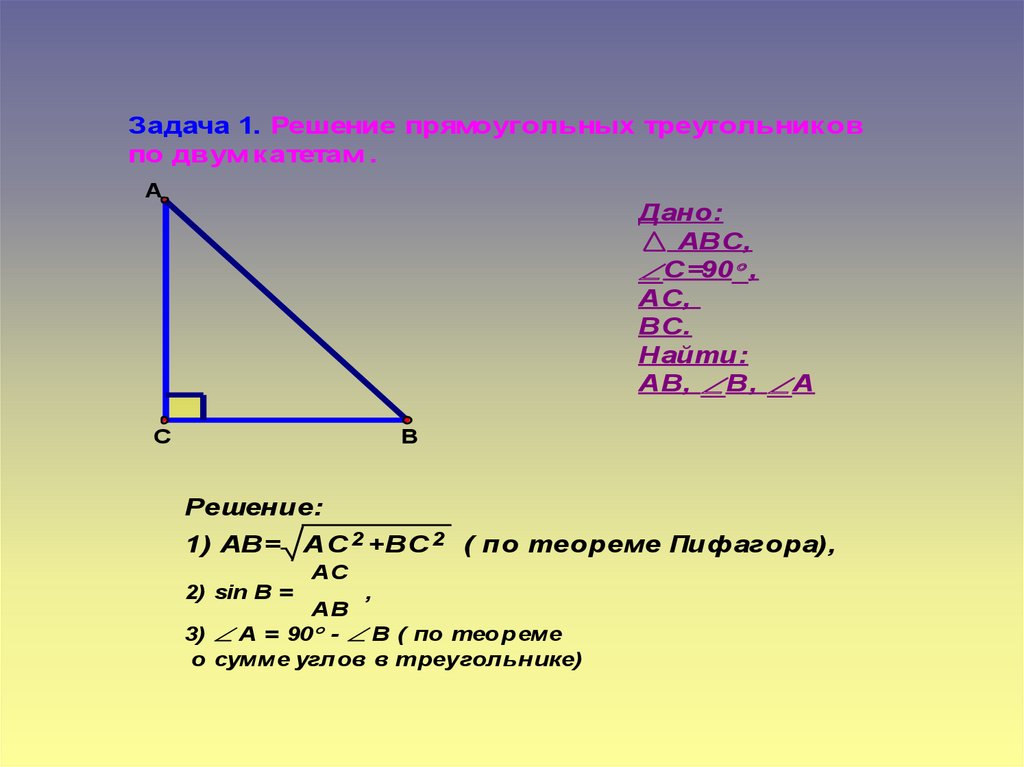
Задача 1. Решение прямоугольных треугольников
по двум катетам .
А
Дано:
АВС,
С=90 ,
АС,
ВС.
Найти:
АВ, В, А
С
B
Решение:
1) АВ= АС 2 +ВС 2 ( по теореме Пифагора),
AC
2) sin B =
,
AB
3) А = 90 - В ( по теореме
о сумме углов в треугольнике)

8.

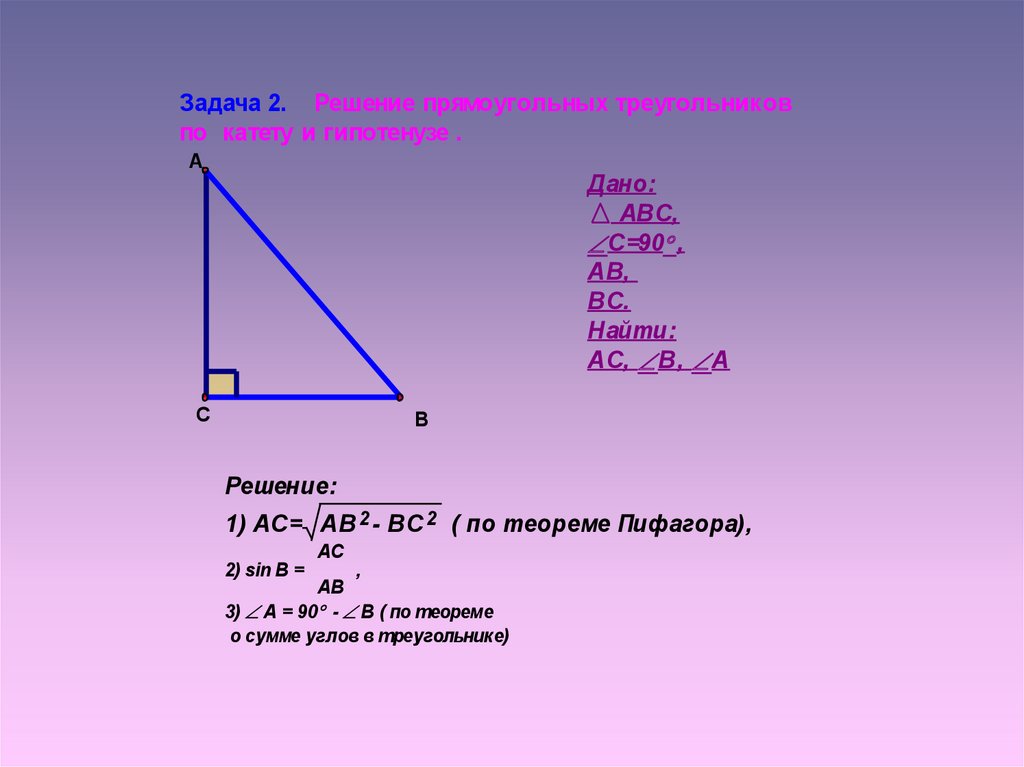
Задача 2. Решение прямоугольных треугольников
по катету и гипотенузе .
А
Дано:
АВС,
С=90 ,
АВ,
ВС.
Найти:
АС, В, А
С
В
Решение:
1) АС= АВ 2 - ВС 2 ( по теореме Пифагора),
AC
2) sin B =
,
AB
3) А = 90 - В ( по теореме
о сумме углов в треугольнике)

9.

Задача 3. Решение прямоугольных треугольников
по катету и прилежащ ему о строму углу .
А
Дано:
АВС,
С=90 ,
ВС,
В.
Найти:
АС, АВ, А
С
В
Решение:
1) А = 90 - В ( по теореме
о сумме углов в треугольнике),
BC
2) cos B =
, АВ = ВС cos B,
AB
3) АС=
АВ 2 - ВС 2 ( по теореме Пифагора),

10.

Задача 4. Решение прямоугольных треугольников
по катету и противолежащ ему углу .
А
С
Дано:
АВС,
С=90 ,
А,
ВС.
Найти:
АВ, АС, В
B
Решение:
1) В = 90 - А ( по теореме
о сумме углов в треугольнике),
ВC
ВС
2) sin А =
, АВ =
,
AB
sin A
3) АC= АB 2 - ВС 2 ( по теореме Пифагора).

11.

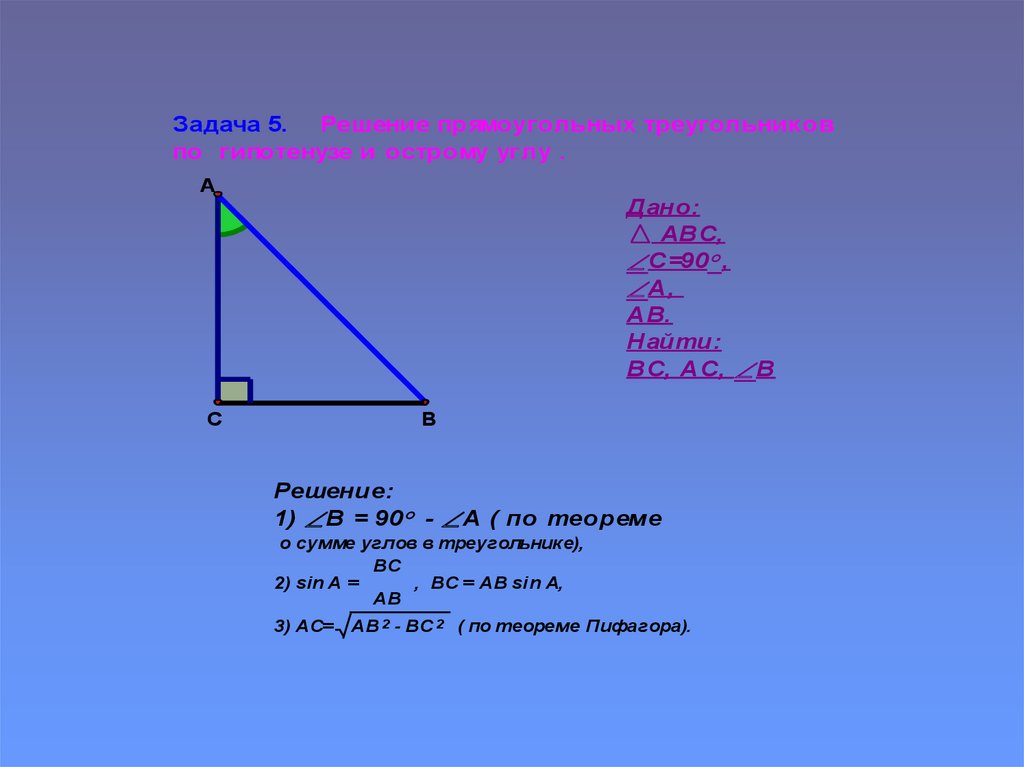
Задача 5. Решение прямоугольных треугольников
по гипотенузе и острому углу .
А
С
Дано:
АВС,
С=90 ,
А,
АВ.
Найти:
ВС, АС, В
B
Решение:
1) В = 90 - А ( по теореме
о сумме углов в треугольнике),
ВC
2) sin А =
, ВС = АВ sin A,
AB
3) АC= АB 2 - ВС 2 ( по теореме Пифагора).

12.

• Теорема синусов
Стороны треугольника
пропорциональны
синусам противолежащих
углов.
В
с
а
• Теорема косинусов
Квадрат стороны
треугольника равен
сумме квадратов двух
других сторон минус
удвоенное произведение
этих сторон на косинус
угла между ними.
В
А
в
С
а : sin A = в : sin B = c : sin C
c
a
А
в
С
а 2 = в2 + с2 - 2вс cos A

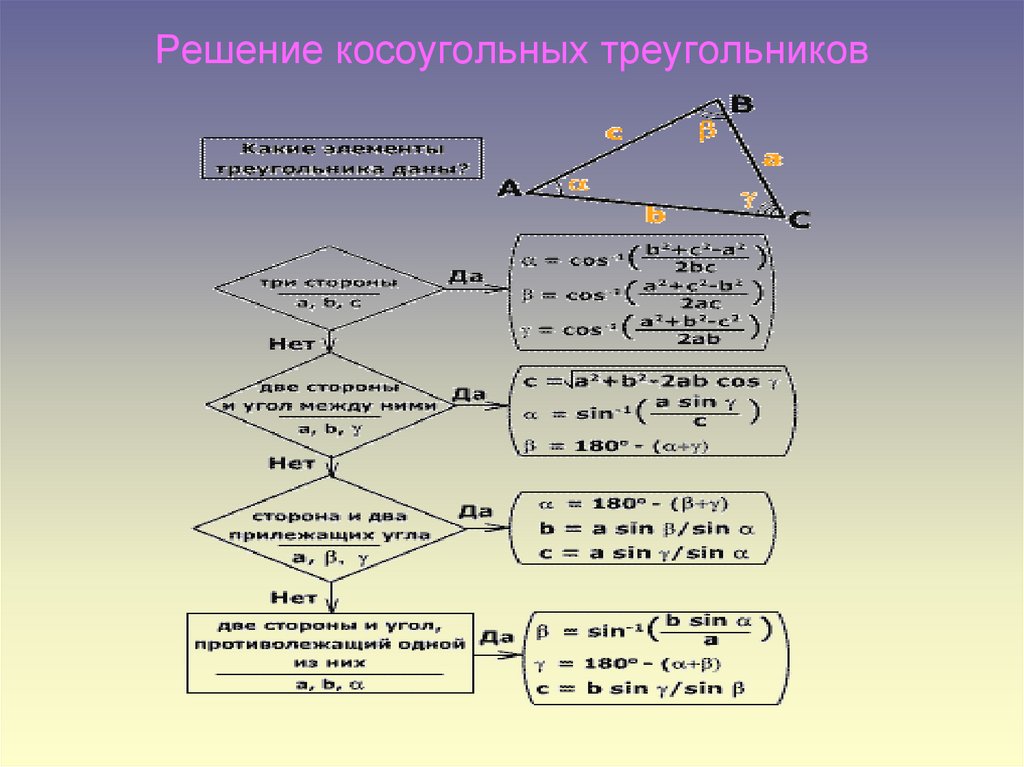
13. Решение косоугольных треугольников

14.

Задача 1.
Решение треуголь ников по двум сто ронам и углу между ними.
В
с
С
А
в
Дано:
АВС,
АВ=с,
АС=в,
А =а.
Найти:
ВС, В, С
Решение:
1 способ:
АВ = 2,97см
АС = 6,45см
<А
1) ВС= в2 + с 2 -2 в c cosа ( по теореме косинусов);
в sinа
2) sin B =
( по теореме синусов);
ВС
3) С=180 - ( А+ В) ( по теореме о сумме
углов треугольн ика).
= 57,84
ВС = 5,48см
<В = 94,82
<С = 27,35
2 способ:
1) sin С=
с sinВ
в
( по теореме синусов);
2) В=180 - ( А+ С ) ( по теореме о
сумме углов треугольника);
в sin A
3) BC =
( по теореме синусов).
sin B

15.

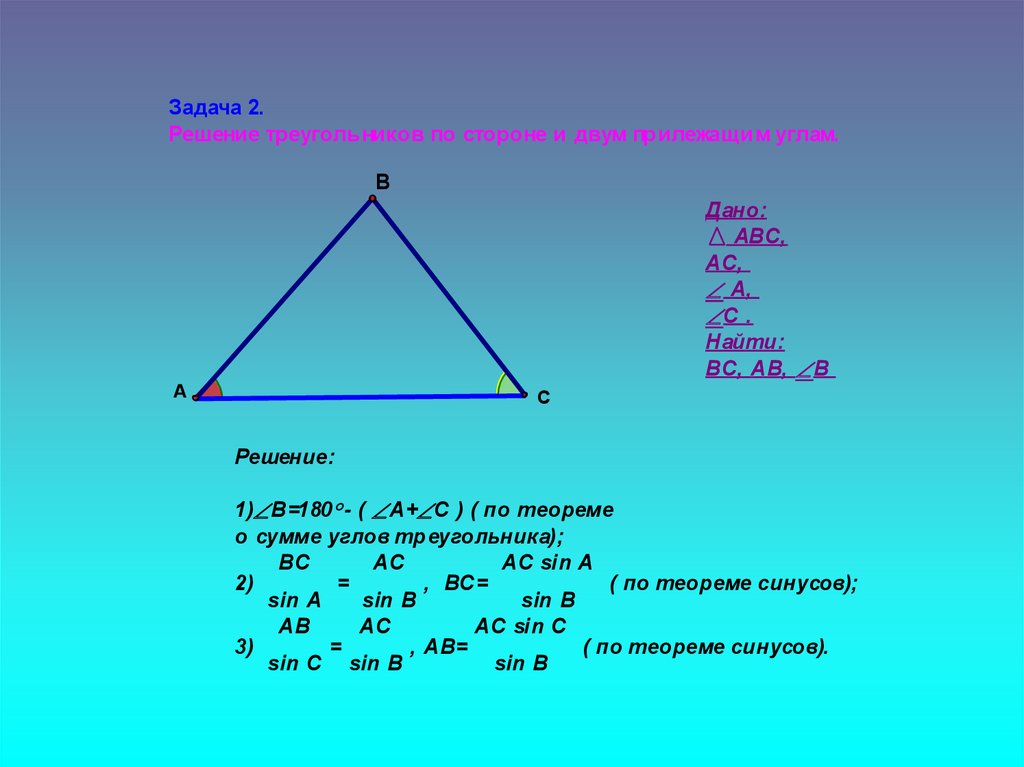
Задача 2.
Решение треугольников по стороне и двум прилежащим углам.
В
Дано:
АВС,
АС,
А,
С .
Найти:
ВС, АВ, В
А
С
Решение:
1) В=180 - ( А+ С ) ( по теореме
о сумме углов треугольника);
ВС
AC
АС sin A
2)
=
, ВС=
( по теореме синусов);
sin A
sin В
sin B
AB
AC
AC sin C
3)
=
, AB=
( по теореме синусов).
sin C sin B
sin B

16.

Задача 3. Решение треуголь ников по трем сто ронам .
В
а
с
А
в
С
Дано:
АВС,
АВ=с,
АС=в,
ВС=а.
Найти:
А, В, С
Решение:
1)с 2 =а 2 +в 2 -2ав
cosC, cos C =
a 2 +b 2 -c 2
2aв
( по теореме косинусов);
2) в 2 = а 2 +с 2 -2ас cos B, cos B =
a 2 +c 2 -в 2
2ас
( по теореме косинусов);
3) А=180 - ( С+ В) ( по теореме о сумме
углов треугольн ика).