Similar presentations:
14. Поворот, параллельный перенос, осевая и центральная симметрия
1.
ОрнаментыПодготовила: учитель математики Шинкоренко М. П.,
МБОУ «Верещакская СОШ»
2.
Поворот3.
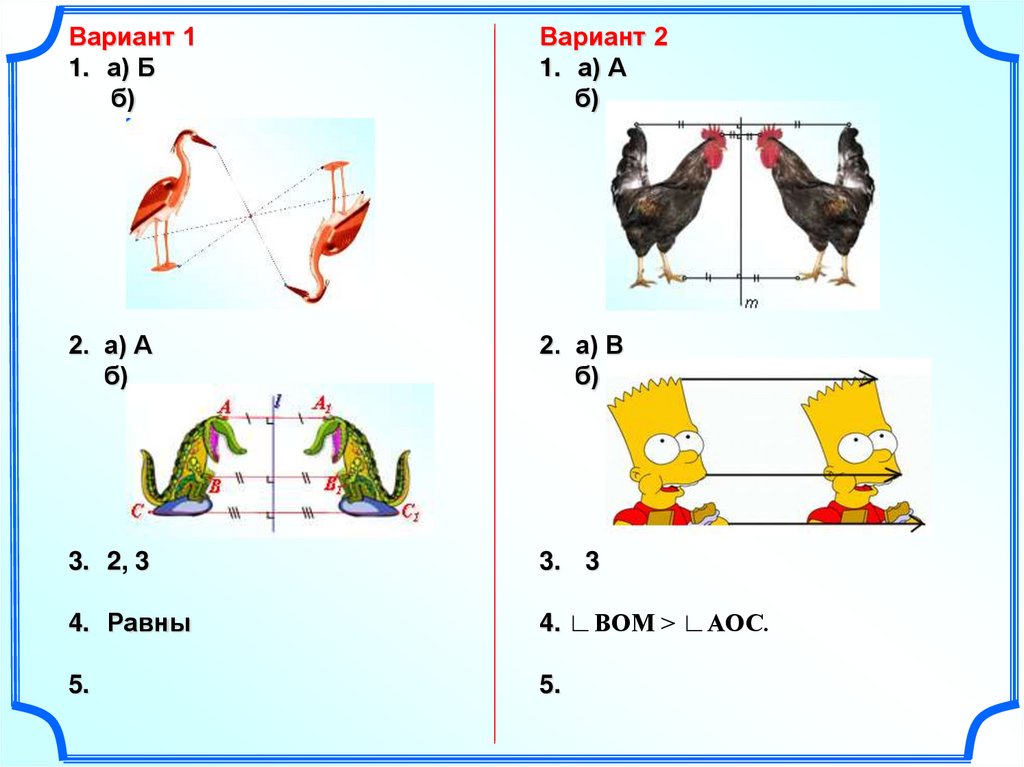
Вариант 11. а) Б
б)
Вариант 2
1. а) А
б)
2. а) А
б)
2. а) В
б)
3. 2, 3
3. 3
4. Равны
4. ∟ВОМ > ∟АОС.
5.
5.
4.
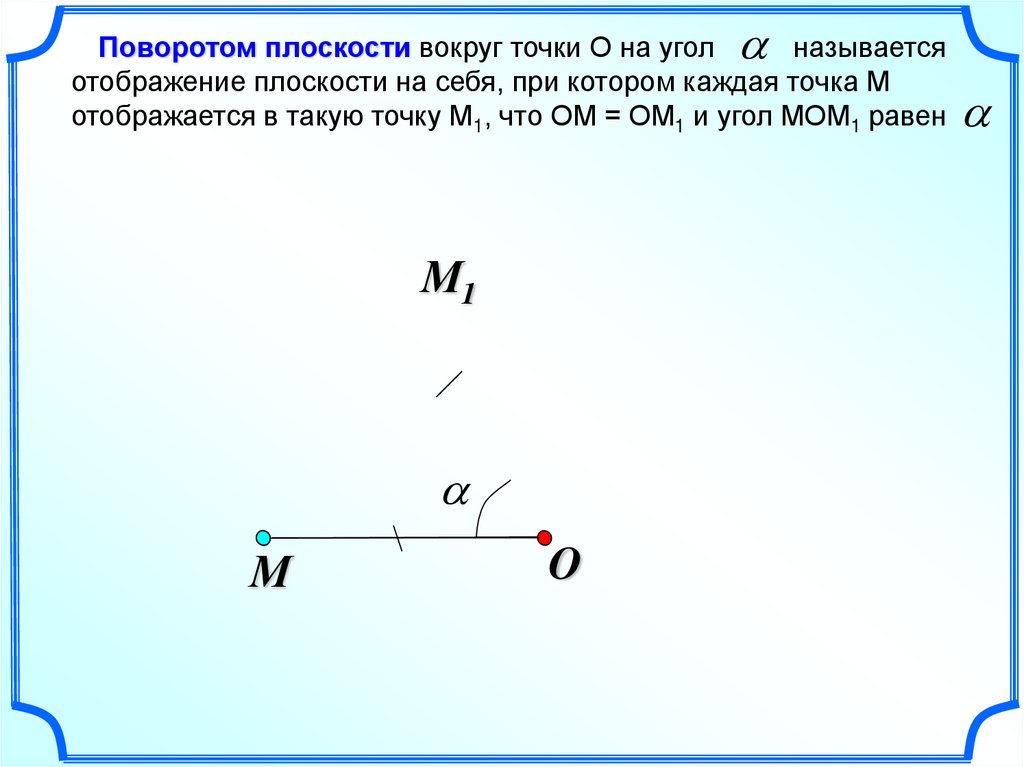
Поворотом плоскости вокруг точки О на уголназывается
отображение плоскости на себя, при котором каждая точка М
отображается в такую точку М1, что ОМ = ОМ1 и угол МОМ1 равен
М1
М
O
5.
Угол поворота 600110
100
130
60
70
100
80
40
30
140
30
150
160
20
170
170
10
180
50
110
130
40
160
М160
120
50
150
70
90
120
140
80
180
0
О
М
20
10
0
6.
Алгоритм построения образа точки М приповороте вокруг точки О на угол α
1. Проводим луч ОМ;
2. Строим ∟МОМ1 = α;
3. Проводим дугу окружности с центром в точке О и радиусом
ОМ до пересечения с лучом ОМ1;
4. Точка пересечения М1 есть образ точки М при повороте на
угол α.
7.
Угол поворота 1200А1
В1
А
О
В
8.
Поворот отрезка.В
C
C1
O
O
D1
В1
D
9.
Дано: поворот.Доказать: поворот является движением.
Доказательство:
1. Поворот точек М и N на угол α против часовой стрелки.
2. ∆ОМN = ∆ОМ1N1
3. МN = М1N1, т. е. поворот является движением.
10.
11.
12.
Голландский художник Морис Корнелиус Эшер создавал картины,используя виды движений: поворот, параллельный перенос, осевую и
центральную симметрию.










 mathematics
mathematics








