Similar presentations:
Основы математической обработки информации
1. Основы математической обработки информации
Рогозин Сергей Анатольевич,старший преподаватель
кафедры информатики ЮУрГГПУ
1
2. План
• 1. Математическая логика каксамостоятельный раздел математики
• 2. Высказывания и операции над ними
2
3. 1. Математическая логика как самостоятельный раздел математики
34.
• Язык математики- математическая логика• Основатели логики – Зенон и Сократ
• Математическая логика – теория,
изучающая правила вывода с помощью
специального аппарата символов и
исчислений (формализованных языков).
• Символы математики называют
кванторами.
4
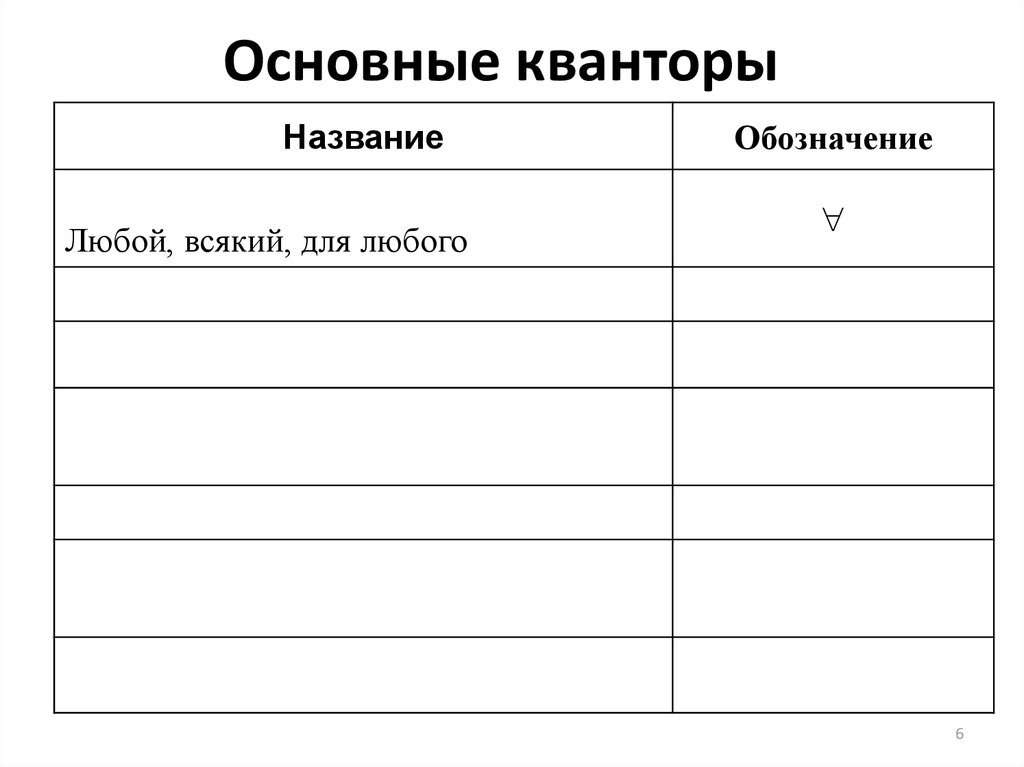
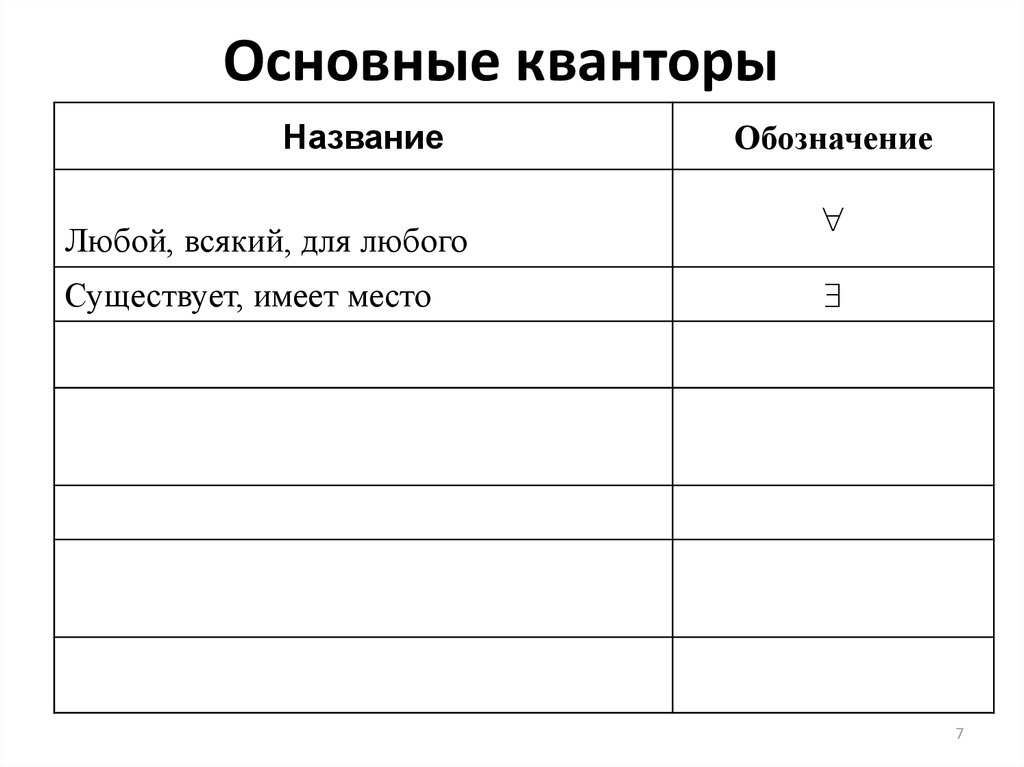
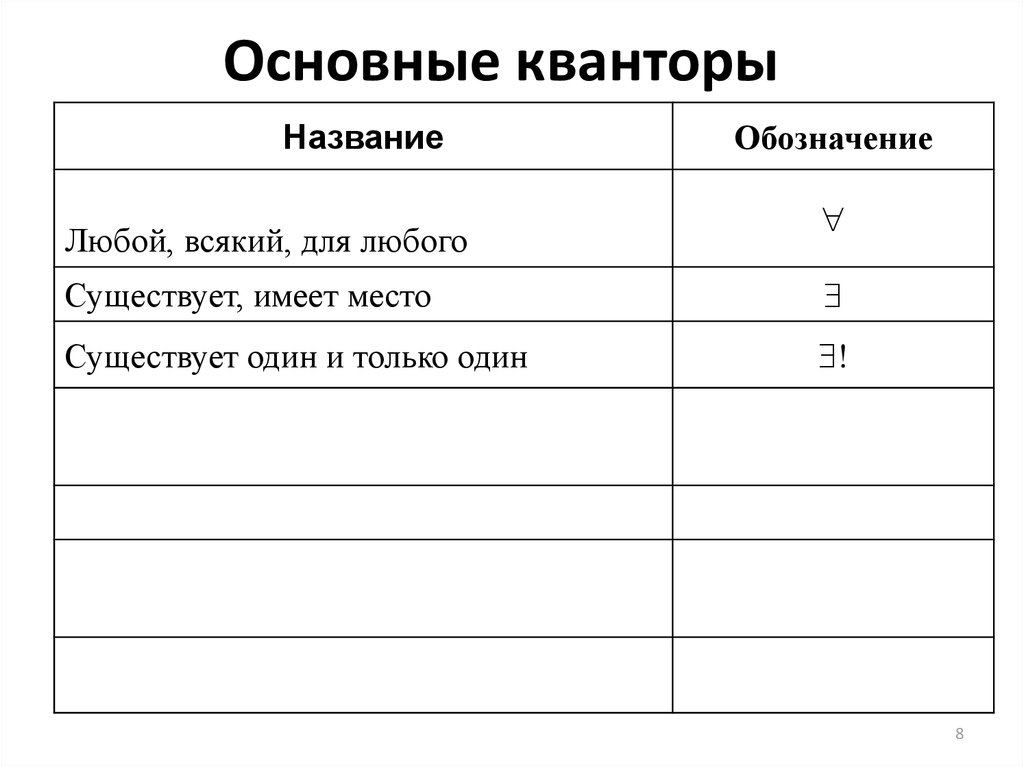
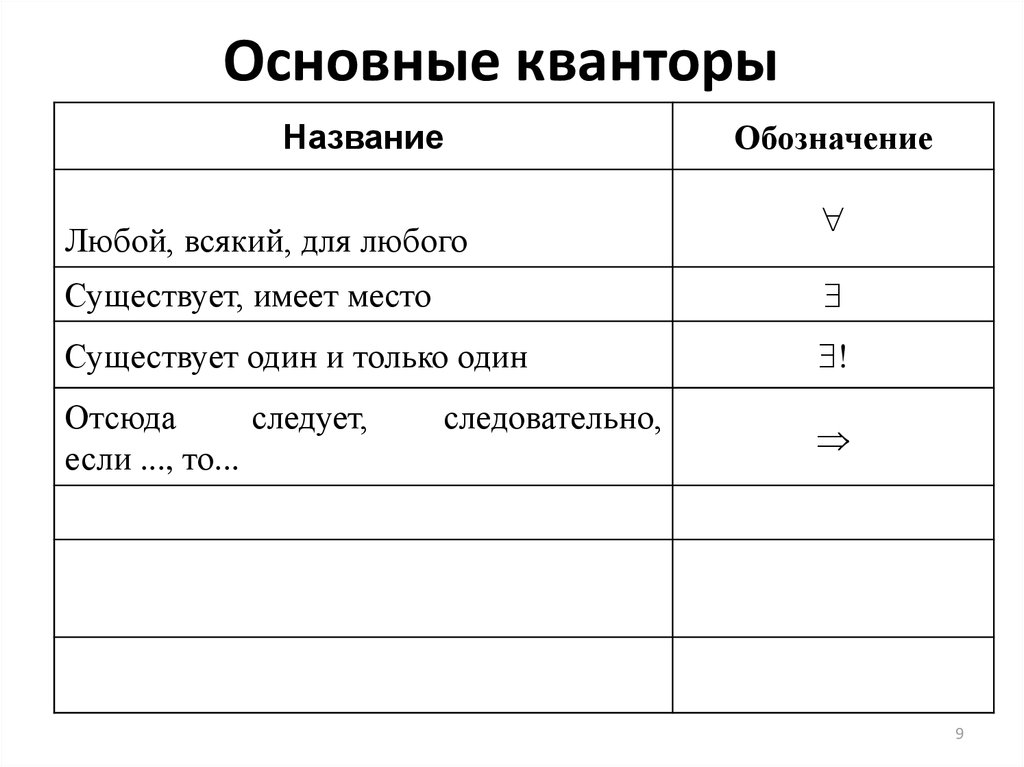
5. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
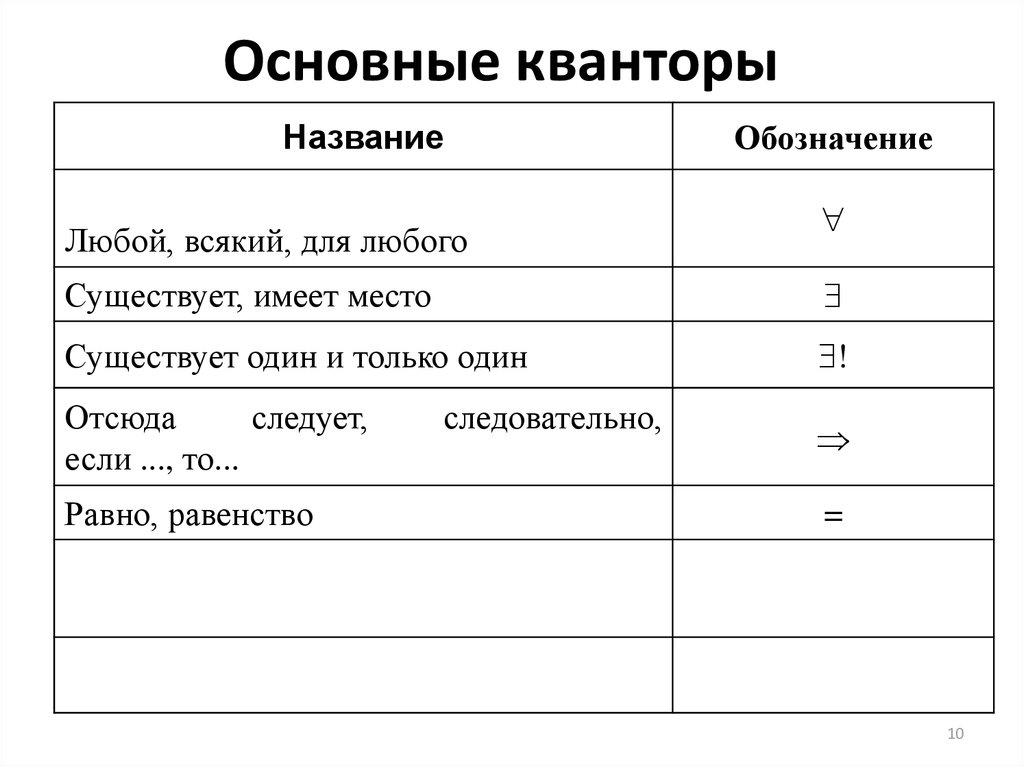
Равно, равенство
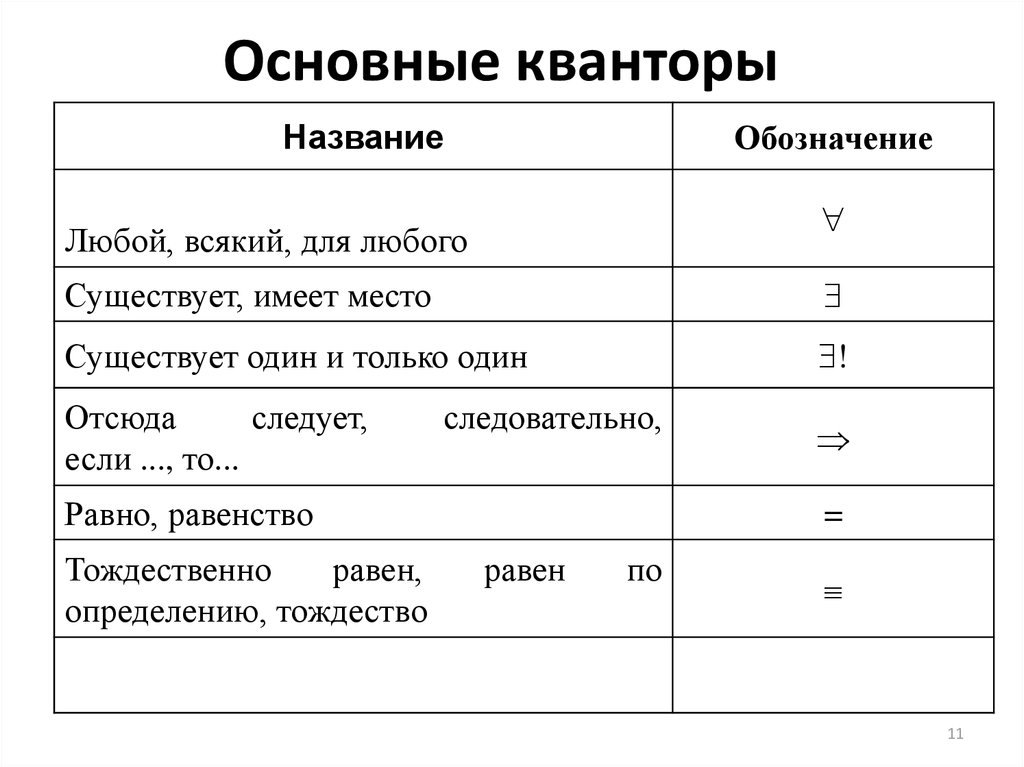
Тождественно
равен,
определению, тождество
=
равен
по
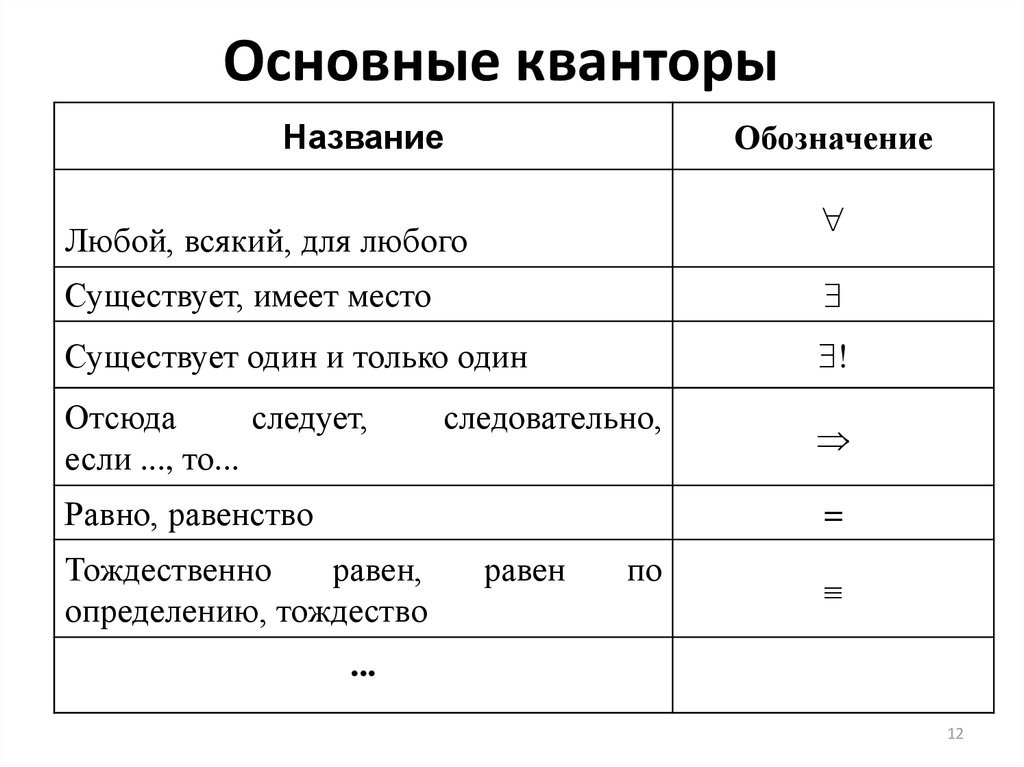
...
5
6. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
Равно, равенство
Тождественно
равен,
определению, тождество
=
равен
по
...
6
7. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
Равно, равенство
Тождественно
равен,
определению, тождество
=
равен
по
...
7
8. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
Равно, равенство
Тождественно
равен,
определению, тождество
=
равен
по
...
8
9. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
Равно, равенство
Тождественно
равен,
определению, тождество
=
равен
по
...
9
10. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
Равно, равенство
Тождественно
равен,
определению, тождество
=
равен
по
...
10
11. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
Равно, равенство
Тождественно
равен,
определению, тождество
=
равен
по
...
11
12. Основные кванторы
НазваниеОбозначение
Любой, всякий, для любого
Существует, имеет место
Существует один и только один
!
Отсюда
следует,
если ..., то...
следовательно,
Равно, равенство
=
Тождественно
равен,
определению, тождество
равен
по
...
12
13. 2. Высказывания и операции над ними
1314.
• Основными объектами, которые изучаетматематическая логика, являются
высказывания.
• Высказывание – повествовательное
утвердительное предложение,
относительно которого можно с
уверенностью сказать, является оно
истинным или ложным.
14
15.
• А, В, С, D … – высказывания• Пример: Сегодня проводится дистанционная
лекция по дисциплине «Математическая
логика»
• Является ли данное предложение
высказыванием?
• Ответ: да, является. Данное предложение
повествовательное, утвердительное, и
относительно его можно сказать, является оно
истинным или ложным.
15
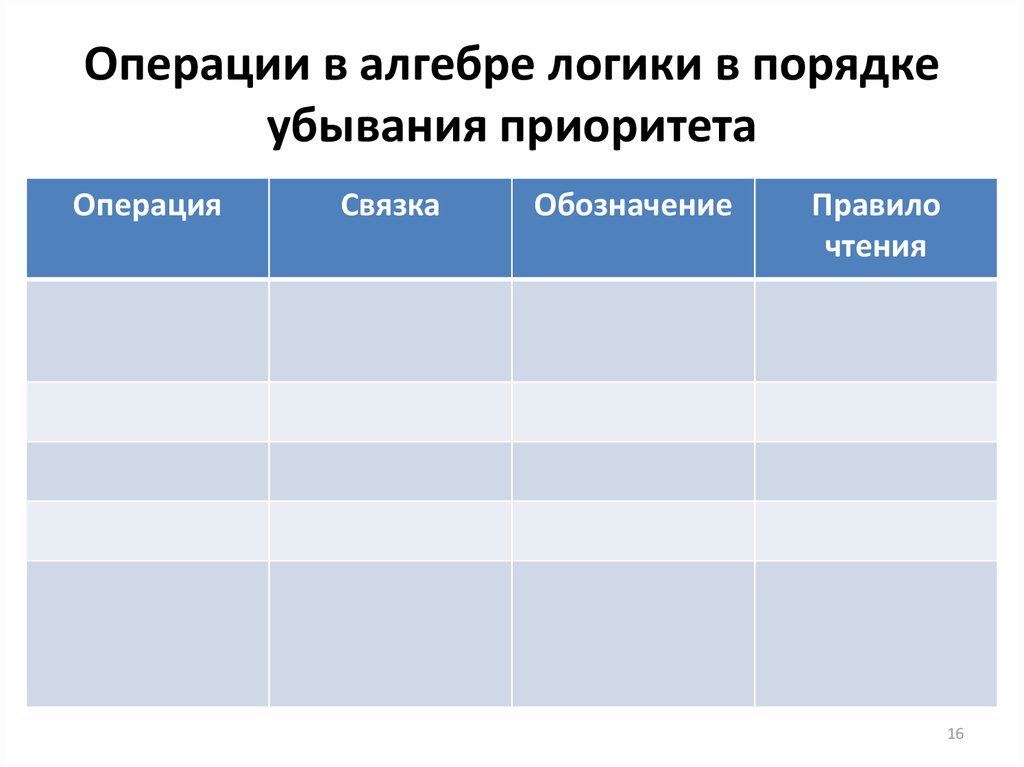
16. Операции в алгебре логики в порядке убывания приоритета
ОперацияСвязка
Обозначение
Правило
чтения
16
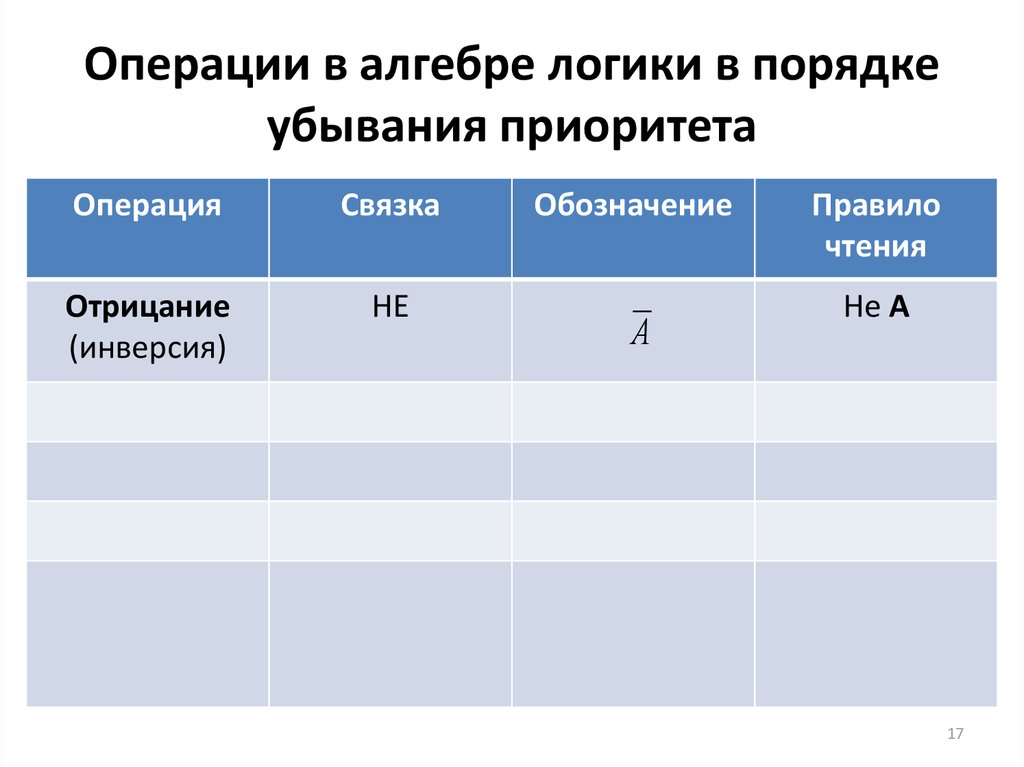
17. Операции в алгебре логики в порядке убывания приоритета
ОперацияСвязка
Отрицание
(инверсия)
НЕ
Обозначение
А
Правило
чтения
Не А
17
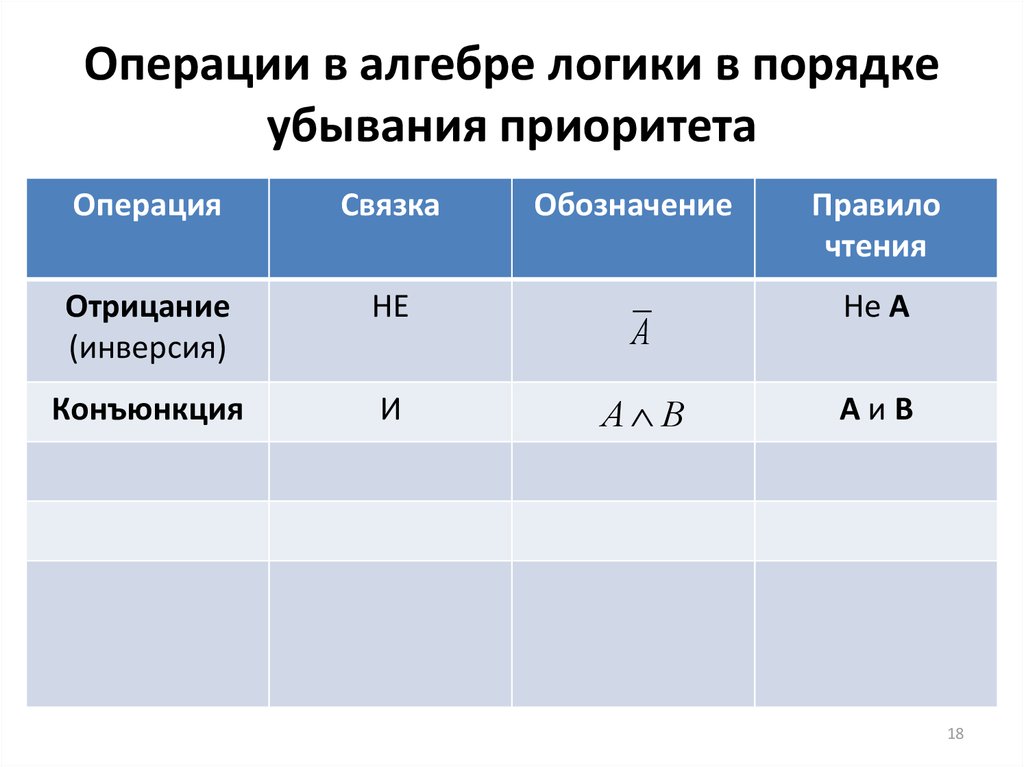
18. Операции в алгебре логики в порядке убывания приоритета
ОперацияСвязка
Отрицание
(инверсия)
НЕ
Конъюнкция
И
Обозначение
А
А В
Правило
чтения
Не А
АиВ
18
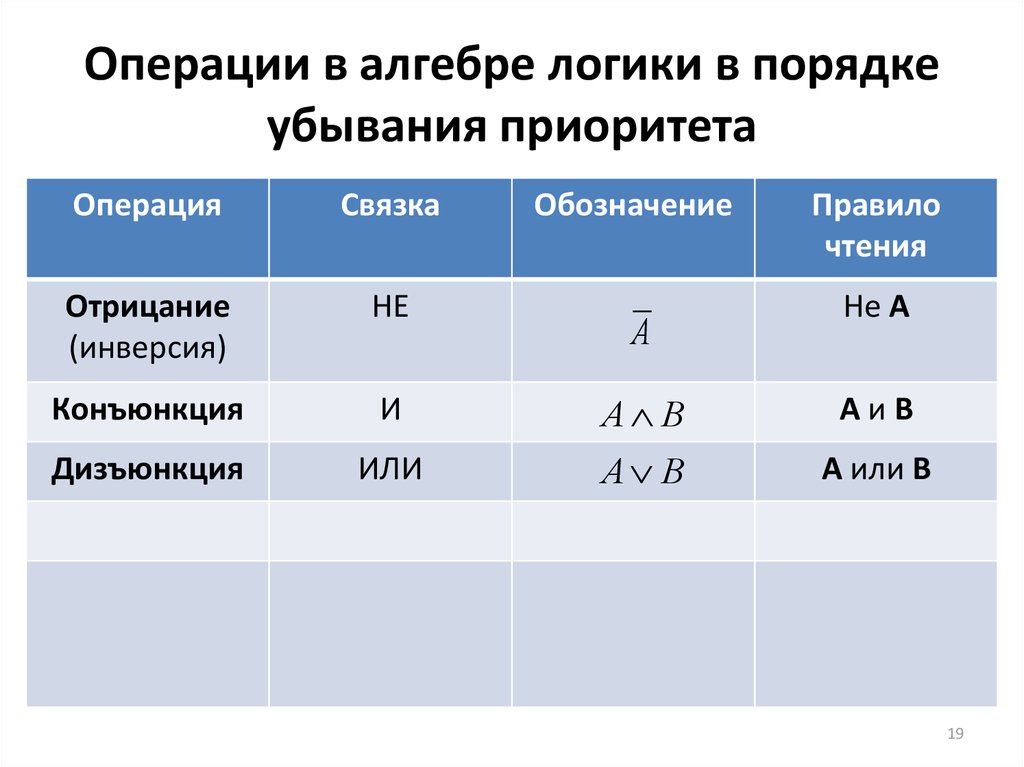
19. Операции в алгебре логики в порядке убывания приоритета
ОперацияСвязка
Отрицание
(инверсия)
НЕ
Конъюнкция
И
Дизъюнкция
ИЛИ
Обозначение
А
А В
А В
Правило
чтения
Не А
АиВ
А или В
19
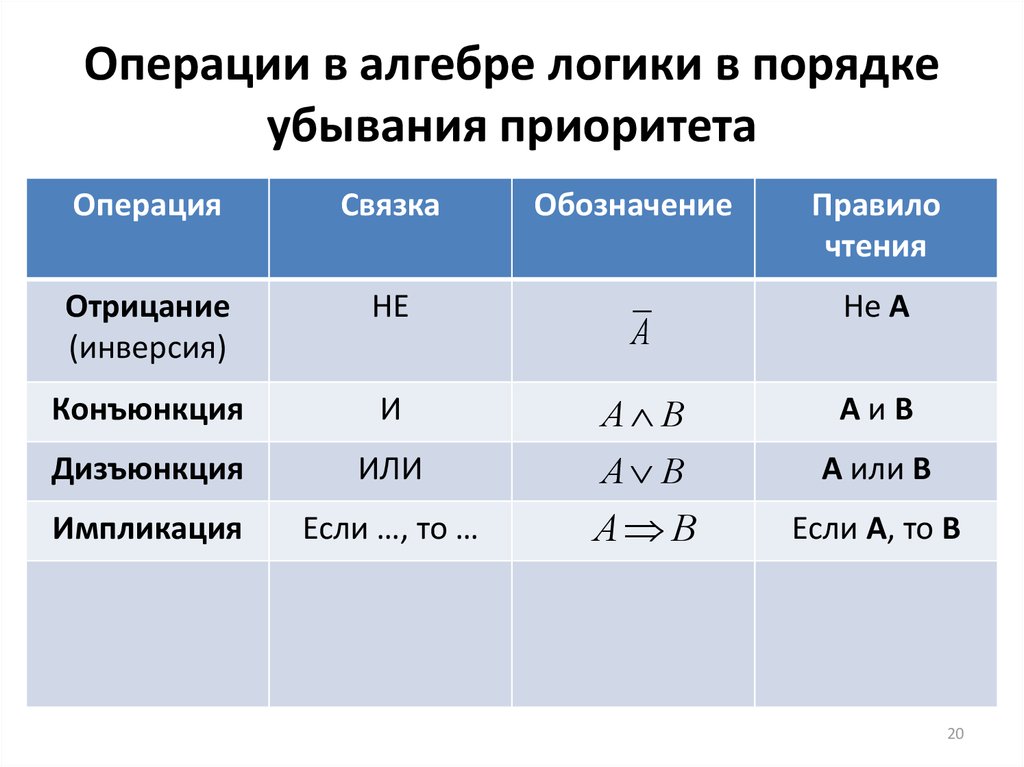
20. Операции в алгебре логики в порядке убывания приоритета
ОперацияСвязка
Отрицание
(инверсия)
НЕ
Конъюнкция
И
Дизъюнкция
Импликация
Обозначение
А
Правило
чтения
Не А
ИЛИ
А В
А В
А или В
Если …, то …
А В
Если А, то В
АиВ
20
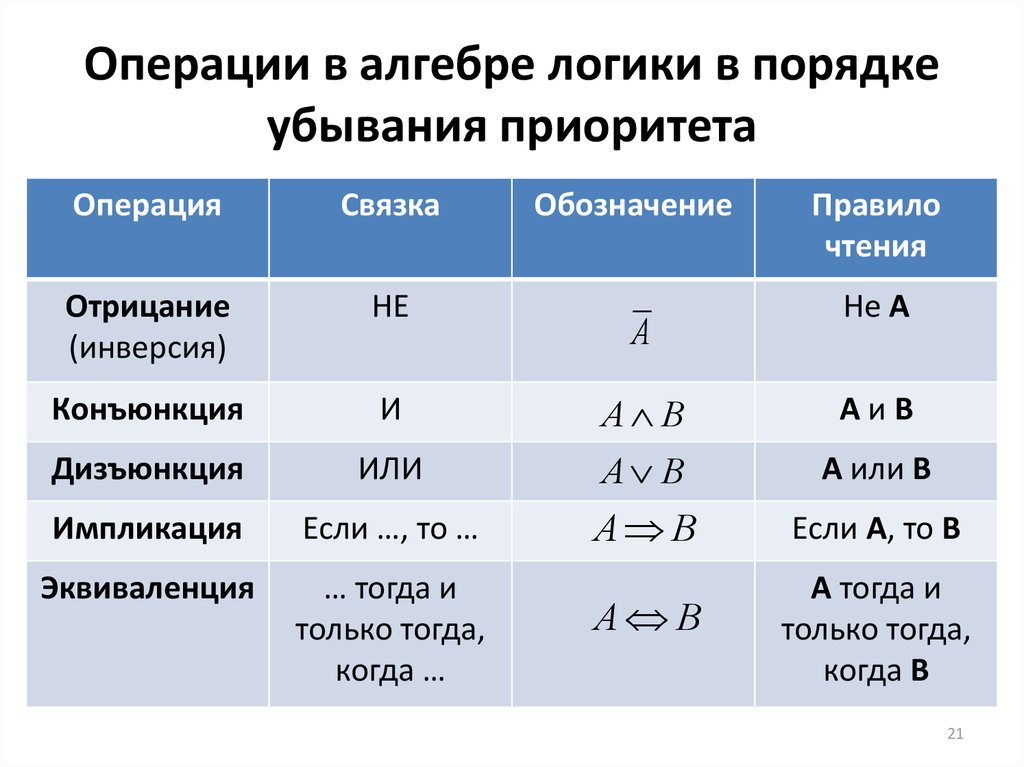
21. Операции в алгебре логики в порядке убывания приоритета
ОперацияСвязка
Отрицание
(инверсия)
НЕ
Конъюнкция
И
Дизъюнкция
Обозначение
А
Правило
чтения
Не А
ИЛИ
А В
А В
А или В
Импликация
Если …, то …
А В
Если А, то В
Эквиваленция
… тогда и
только тогда,
когда …
А В
А тогда и
только тогда,
когда В
АиВ
21
22. Как обозначаются истинность и ложность высказывания?
• И – истина (true) • Л – ложь (false) -1
0
• Количество состояний при составлении
таблицы истинности определяется по
n
формуле 2 , где n – число высказываний
22
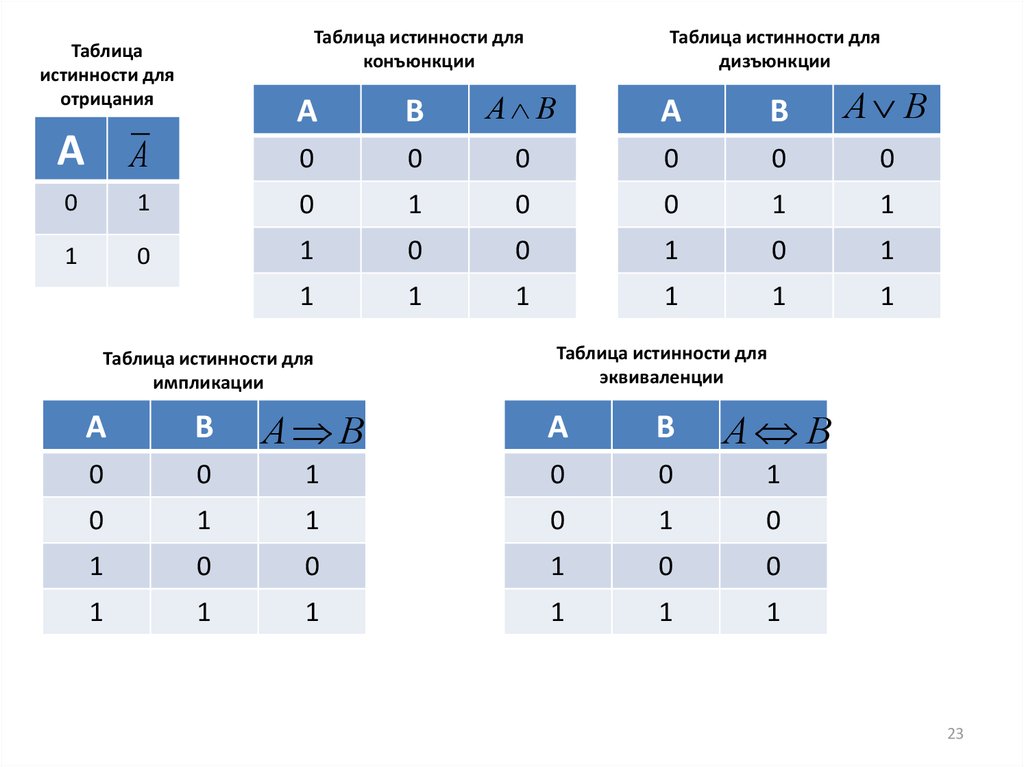
23.
Таблица истинности дляконъюнкции
Таблица
истинности для
отрицания
Таблица истинности для
дизъюнкции
А
В
А В
А
В
А В
А А
0
0
0
0
0
0
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
1
1
1
1
1
1
Таблица истинности для
импликации
Таблица истинности для
эквиваленции
А
В
А В
А
В
А В
0
0
1
0
0
1
0
1
1
0
1
0
1
0
0
1
0
0
1
1
1
1
1
1
23
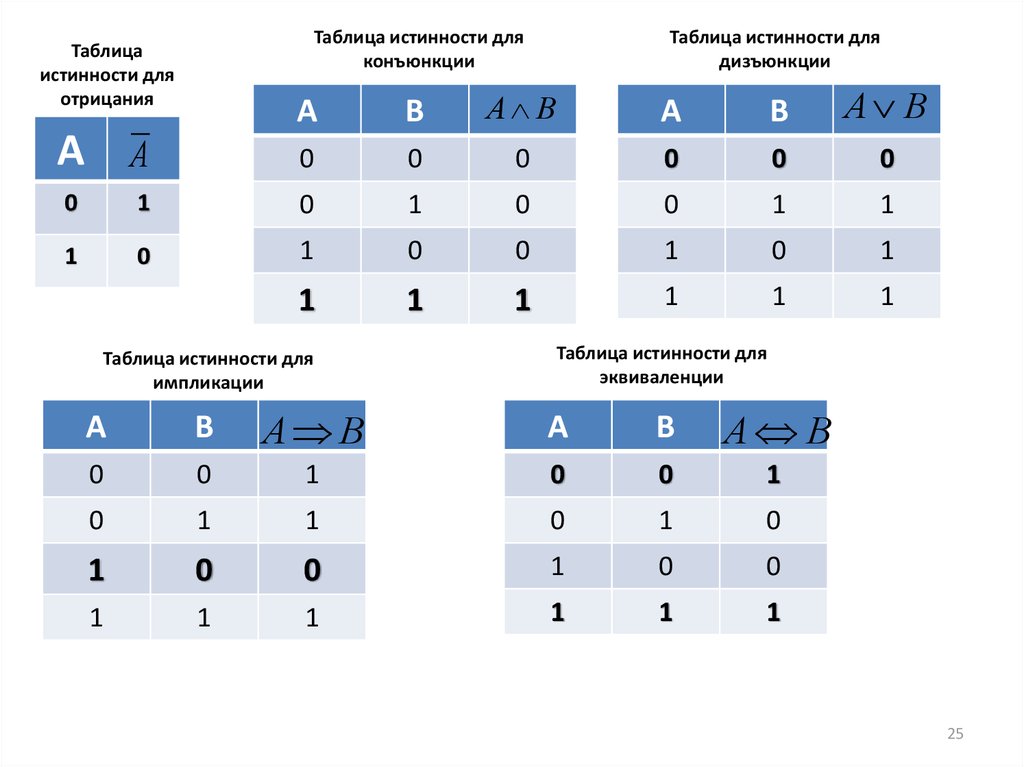
24.
• На следующем слайде выделены те строки,которые необходимо запомнить
24
25.
Таблица истинности дляконъюнкции
Таблица
истинности для
отрицания
Таблица истинности для
дизъюнкции
А
В
А В
А
В
А В
А А
0
0
0
0
0
0
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
1
1
1
1
1
1
Таблица истинности для
импликации
Таблица истинности для
эквиваленции
А
В
А В
А
В
А В
0
0
1
0
0
1
0
1
1
0
1
0
1
0
0
1
0
0
1
1
1
1
1
1
25
26. Основные свойства операций
2627.
• Свойство отрицания:А А
27
28.
• Свойства конъюнкции:– Коммутативность
А В В А
– Ассоциативность ( А В ) С
– Идемпотентность
А (В С)
А А А
28
29.
• Свойства дизъюнкции:– Коммутативность
А В В А
– Ассоциативность ( А
– Идемпотентность
В) С А ( В С )
А А А
29
30. Таблица истинности для дизъюнкции
• Свойства дизъюнкции:– Дистрибутивность конъюнкции относительно
дизъюнкции
А ( В С ) ( А В) ( А С )
– Дистрибутивность дизъюнкции относительно
конъюнкции
А ( В С ) ( А В) ( А С )
30
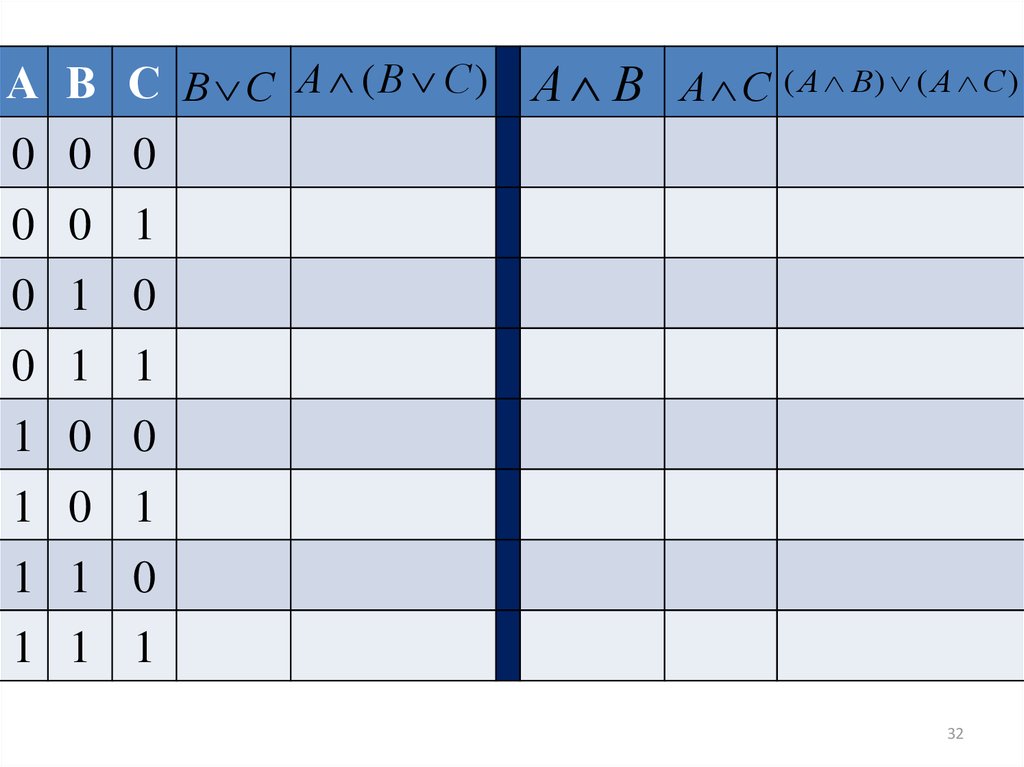
31. Докажем:
А ( В С ) ( А В) ( А С )Чтобы доказать данное равенство, построим
таблицу истинности. Докажем, что левая часть
равенства равняется правой.
31
32.
А В С В С А ( В С ) А В А С ( А В) ( А С )0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
32
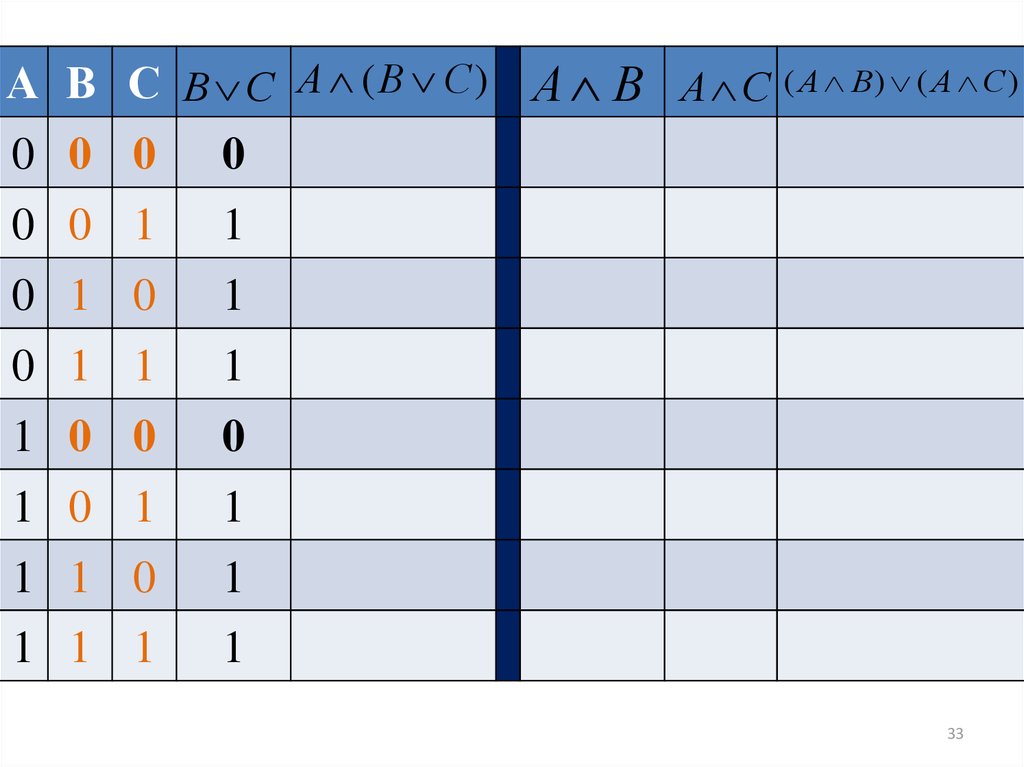
33.
А В С В С А ( В С ) А В А С ( А В) ( А С )0 0 0 0
0 0 1
1
0 1 0
1
0 1 1
1
1 0 0
0
1 0 1
1
1 1 0
1
1 1 1
1
33
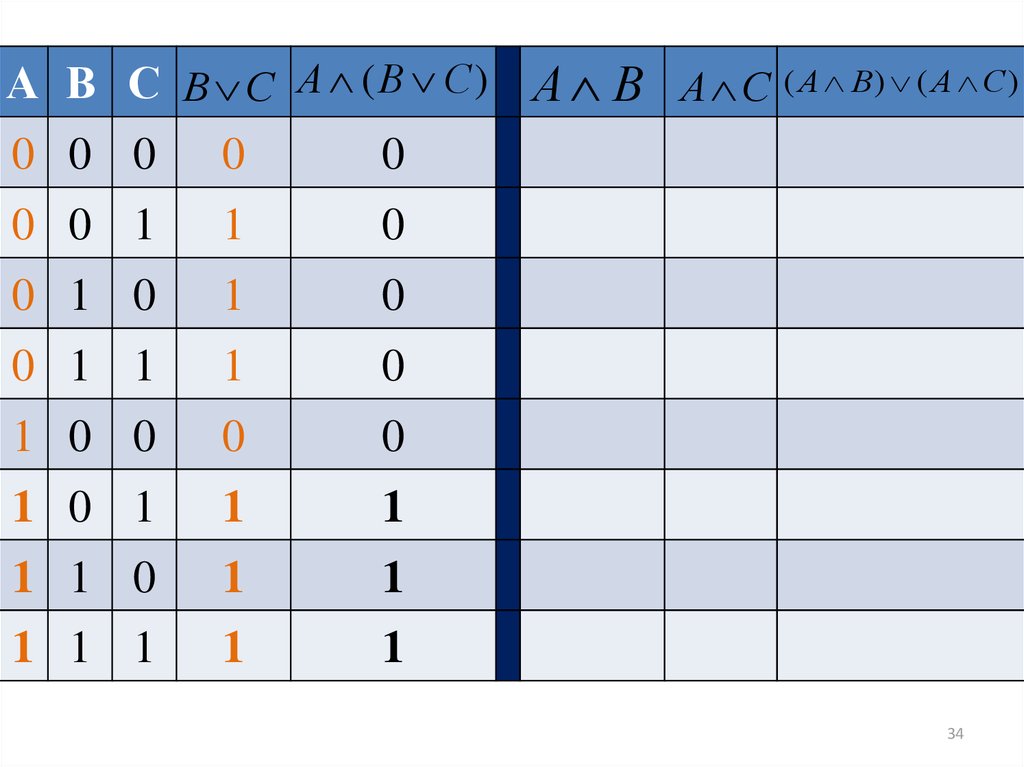
34.
А В С В С А ( В С ) А В А С ( А В) ( А С )0 0 0 0
0
0 0 1
1
0
0 1 0
1
0
0 1 1
1
0
1 0 0
0
0
1 0 1
1
1
1 1 0
1
1
1 1 1
1
1
34
35.
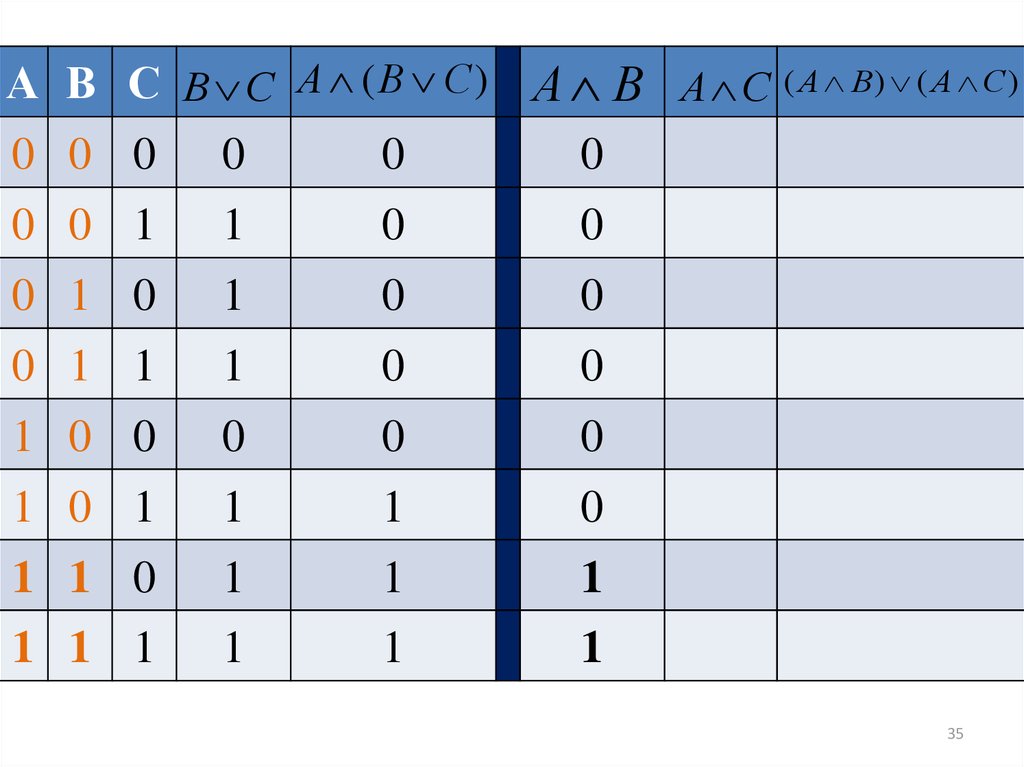
А В С В С А ( В С ) А В А С ( А В) ( А С )0 0 0 0
0
0
0 0 1
1
0
0
0 1 0
1
0
0
0 1 1
1
0
0
1 0 0
0
0
0
1 0 1
1
1
0
1 1 0
1
1
1
1 1 1
1
1
1
35
36.
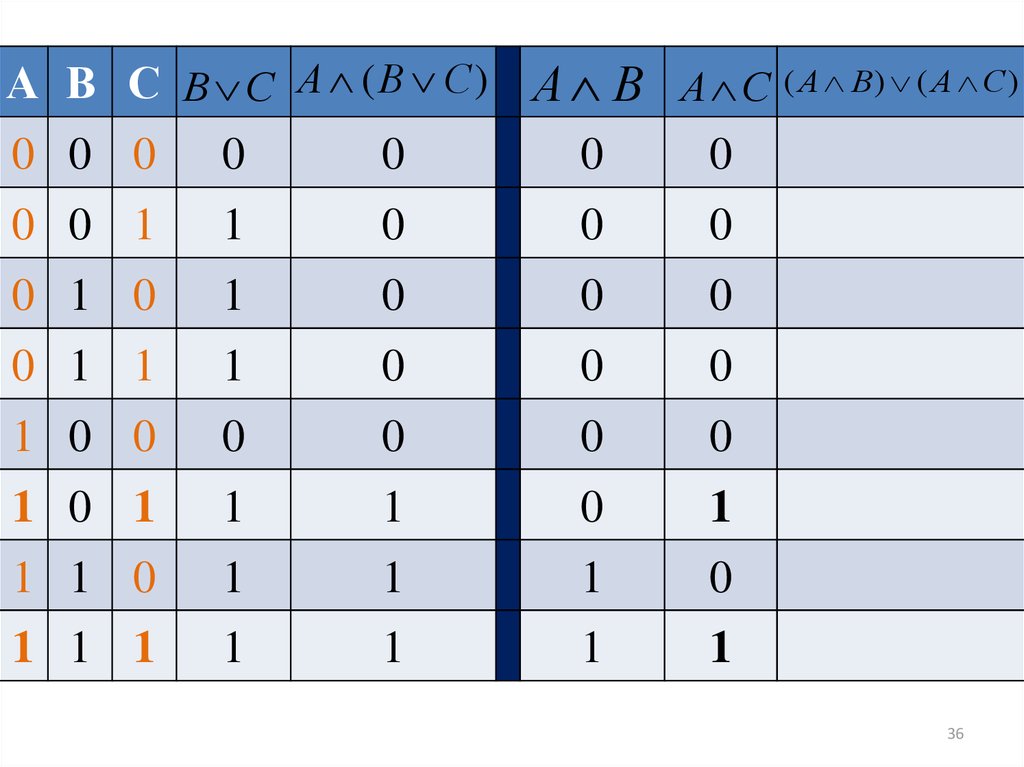
А В С В С А ( В С ) А В А С ( А В) ( А С )0 0 0 0
0
0
0
0 0 1
1
0
0
0
0 1 0
1
0
0
0
0 1 1
1
0
0
0
1 0 0
0
0
0
0
1 0 1
1
1
0
1
1 1 0
1
1
1
0
1 1 1
1
1
1
1
36
37.
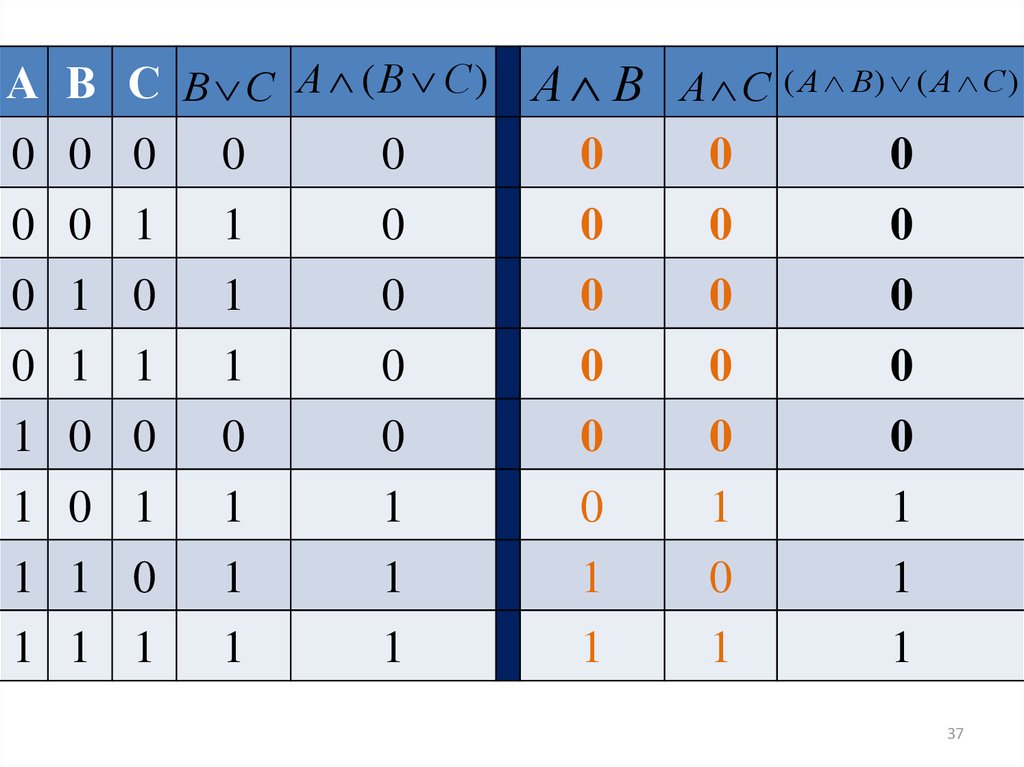
А В С В С А ( В С ) А В А С ( А В) ( А С )0 0 0 0
0
0
0
0
0 0 1
1
0
0
0
0
0 1 0
1
0
0
0
0
0 1 1
1
0
0
0
0
1 0 0
0
0
0
0
0
1 0 1
1
1
0
1
1
1 1 0
1
1
1
0
1
1 1 1
1
1
1
1
1
37
38.
А В С В С А ( В С ) А В А С ( А В) ( А С )0 0 0 0
0
0
0
0
0 0 1
1
0
0
0
0
0 1 0
1
0
0
0
0
0 1 1
1
0
0
0
0
1 0 0
0
0
0
0
0
1 0 1
1
1
0
1
1
1 1 0
1
1
1
0
1
1 1 1
1
1
1
1
1
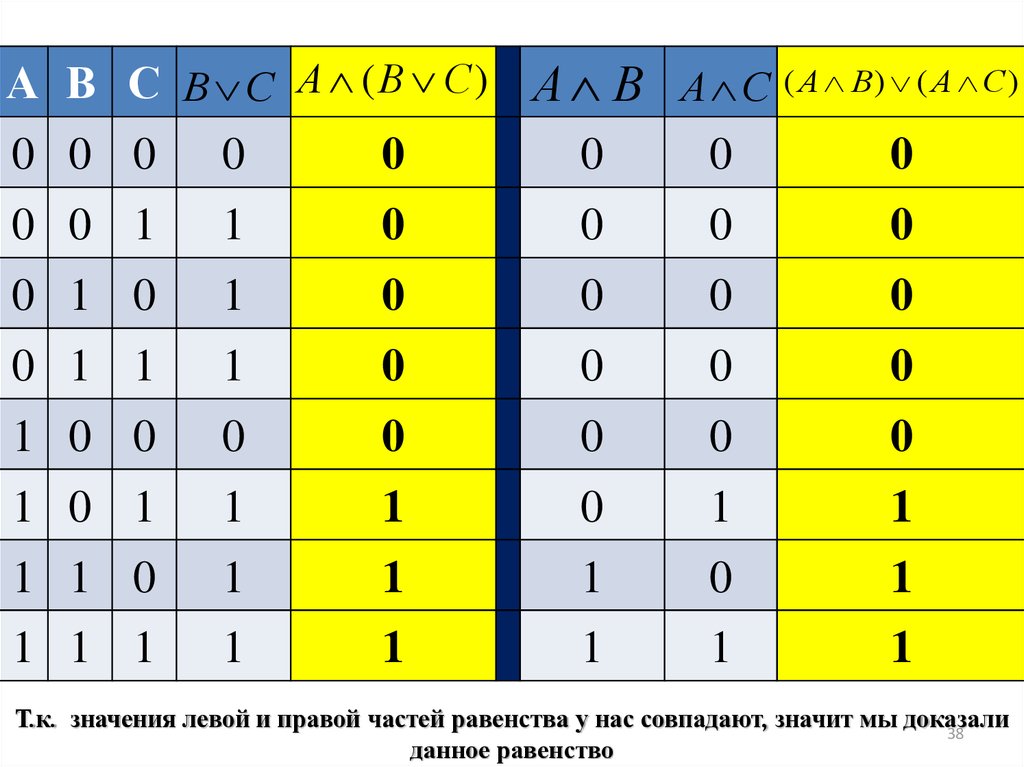
Т.к. значения левой и правой частей равенства у нас совпадают, значит мы доказали
38
данное равенство










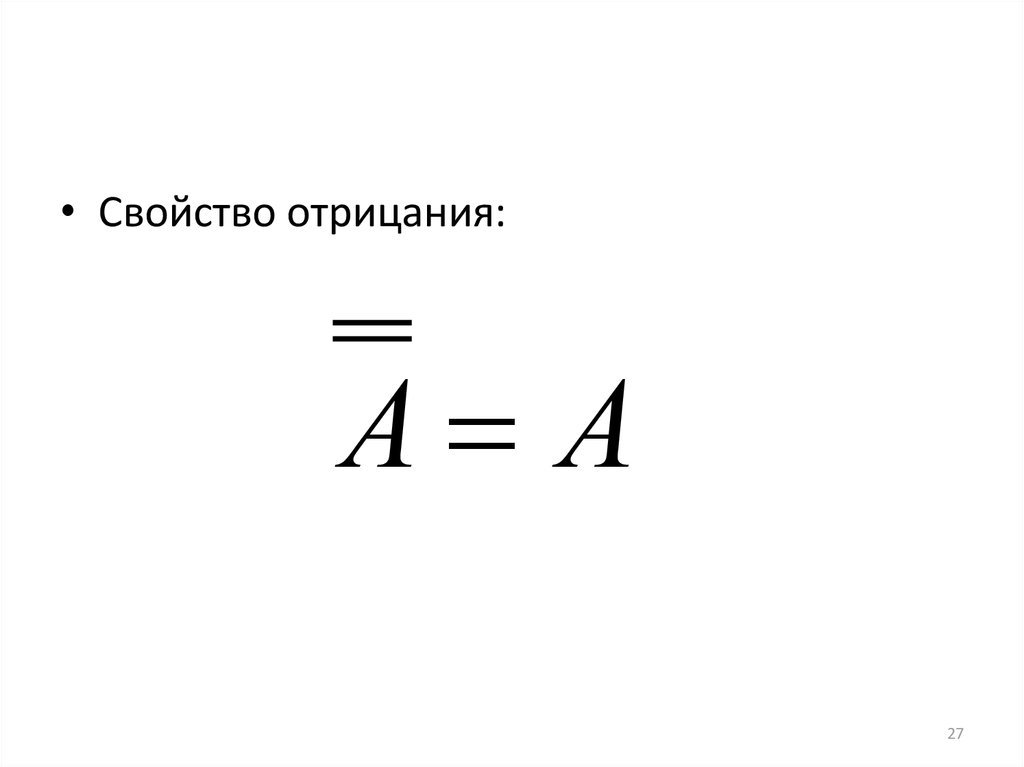




 mathematics
mathematics








