Математическая логика

1. Математическая логика

Ревягина Т.Л.

2. Правила пользования презентацией

Возврат к предыдущему слайду
Переход к следующему слайду
Подчёркнутое Гиперссылка
слово
Выход в содержание

3. Содержание

4. Предисловие

В повседневной жизни мы часто
сталкиваемся с ситуациями, когда не
знаем, как прийти к выводу из предпосылок
и получить истинное знание о предмете
размышления. Логика служит одним из
инструментов почти любой науки.

5. Предмет логики

6. История

Реализация идеи Лейбница
Как самостоятельная
Впервые
в истории идеи наука
о
принадлежит английскому учёному Д.
логика оформилась
построении
логики нав трудах
Булю. Он создал алгебру, в которой
буквами обозначены высказывания.
греческого философа
математической
основе были
Введение символических обозначений
Аристотеля
(384-322
г.г до
высказаны
немецким
математиком
н.э.). Он систематизировал
Г. Лейбницем
(1646-1716) в конце XVII в логику имело для этой науки такое
же решающее значение, как и введение
известные
до него
века.
Он считал,
что сведения,
основные и
буквенных обозначений для
эта система
понятия
логикистала
должны быть
математики. Именно благодаря
впоследствии
называться
обозначены
символами,
которые
введению символов в логику была
формальнойпоили
соединяются
особым правилам. получена основа для создания новой
Аристотелевой
логикой.
Это
позволит всякое
рассуждение науки – МАТЕМАТИЧЕСКОЙ
ЛОГИКИ
заменить вычислением.

7. Высказывания

Понятие высказывания является исходным понятием
математической логики.
Высказывание – утвердительное предложение, относительно
которого можно сказать истинно оно или ложно.
Обычно высказывания обозначаются заглавными
латинскими буквами, а само предложение заключается в
фигурные скобки.

8. Алгебра высказываний

Отрицание
Дизъюнкция
Конъюнкция
Эквиваленция
Импликация

9. Приоритет выполнения операций

4
Аν(В
1
3
2
5
1
С) ∧ А → (ВνС)
1. Действия в скобках
2. Отрицание
3. Конъюнкция
4. Дизъюнкция
5. Импликация, эквиваленция

10. Законы математической логики

Коммутативность
Аν В
А∧ В
Ассоциативность
А ν (В ν С ) А ∧ ( В ∧ С )
Дистрибутивность
А ∧(В ν С )
А ν (В ∧ С )
Законы де Моргана
А ν∧ В
А ν∧ В

11. Законы алгебры логики

1. А = А
6. A ∧ (A ∧ A) = A
2. А ν А = А
7. 0= 1
3. А ∧ А = А
4. А ν А = 1
5. A ν (A ν A) = 1
8. A ν 0 = A
9. A ∧ 0 = A
10. A ∧ A = 0
1 – тождественно-истинное высказывание
0 – тождественно-ложное высказывание

12. Отрицание

Отрицанием высказывания А
называется такое высказывание, что В
ложно, когда А истинно и В истинно,
когда А ложно.
А=В
А
А
1
0
0
1

13. Дизъюнкция

Дизъюнкцией высказываний А и В
называется такое высказывание АνВ,
ложное лишь в том случае, если оба
высказывания А и В ложные.
А
и
и
л
л
В
и
л
и
л
A ≡{Луна - спутник Земли}
В ≡{Солнце- спутник Земли }
АνВ ≡ {Луна - спутник Земли или
Солнце - спутник Земли}
АνВ
и
и
и
л

14. импликация

Импликацией высказываний А и В называется
такое высказывание А→В, ложное лишь в том
случае, когда высказывание А – истинное и В –
ложное.
А
В
А→В
и
и
и
и
л
л
л
и
и
л
л
и
A ≡ {Лето жаркое},
B ≡ {Зима будет холодной}
А→В ≡ {Eсли лето жаркое, то зима будет
холодной.}

15. конъюнкция

Конъюнкцией высказываний А и В
называется такое высказывание А∧В,
истинное лишь в том случае, если оба
высказывания А и В истинные.
А
и
и
В
и
л
А∧В
и
л
л
л
и
л
л
л
А∧В ≡ {Наталья и
Людмила учатся
вместе в 11 а классе}
A ≡{Наталья учится в
В ≡{Людмила учится в
11 а классе}
11 а классе}

16. эквиваленция

Эквиваленцией высказываний А и В
называется такое высказывание А В,
истинное когда А и В – оба истинные
или оба ложные высказывания.
A ≡{Убийство раскрыто},
B ≡{Есть свидетели}
А
В
1
1
0
0
1
0
1
0
Для того чтобы раскрыть убийство
необходимо и достаточно найти
свидетелей.
А
В
1
0
0
1

17.

Тогда,
слушайте
Вы готовы
?
Я не загадку!
слышу!!
Так точно,
Да, капитан!
капитан!
Согласно инструкции я должен находиться на
судне всегда, за исключением случаев, когда с судна
выгружают груз, если же груз не выгружают, то
рулевой никогда не отсутствует, если не
отсутствую и я. В каких случаях рулевой обязан
присутствовать на судне?

18. Разгадали? Давайте проверим

Пусть А≡{Капитан присутствует на судне},
В≡{С судна выгружают груз},
С≡{Рулевой присутствует на судне}, тогда
(В → А) и (B→ (A→C)) – истинные высказывания.
Конъюнкция истинных высказываний истинна, т.е.
(B→A)∧(B→ (A→C))=(BvA)(B→(AvС))= (BvA)(Bv (AvС))=
BvA(AvС)= BvLvAC= BvAC= B→AC.
Проанализировав полученное, выяснили, что рулевой
присутствует на судне, если с судна не выгружают груз.
Ответ: рулевой присутствует на судне,
если с судна не выгружают груз.

19. Предикаты

Утверждение, зависящее от
переменной, заданной на
определенном множестве и
обращающееся в верное
высказывание при
конкретном значении
переменной, называется
неопределенным
высказыванием или
предикатом.
d
A(х) ≡ {d=x+34}

20.

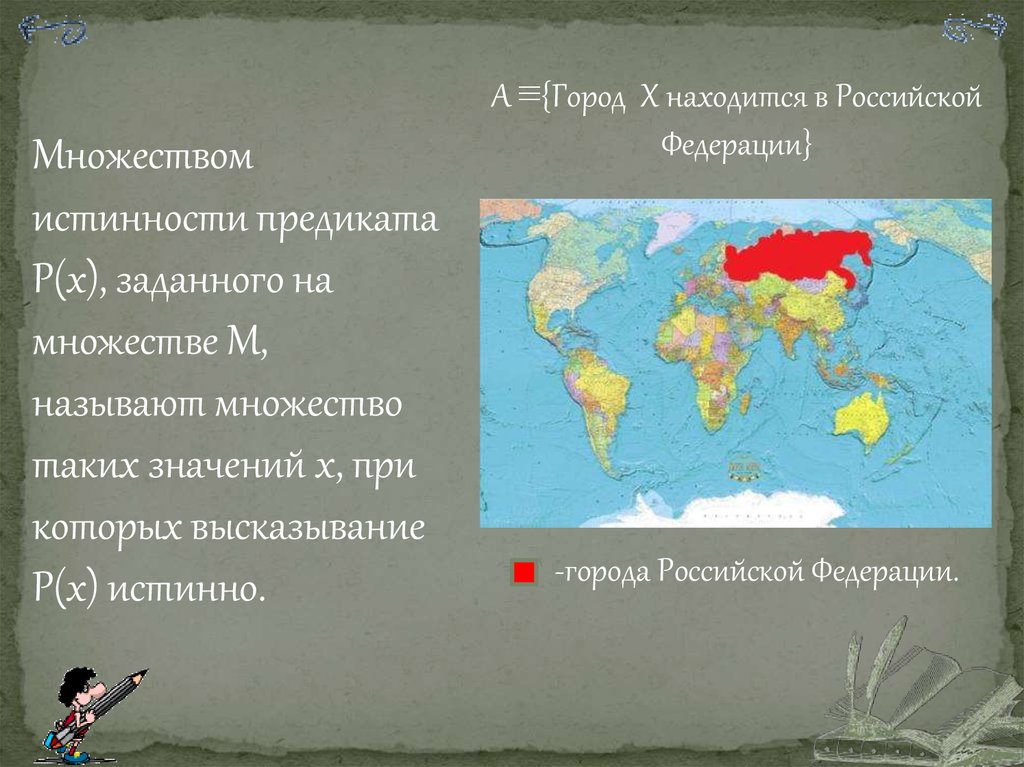
Множеством
истинности предиката
Р(х), заданного на
множестве М,
называют множество
таких значений х, при
которых высказывание
Р(х) истинно.
A ≡{Город Х находится в Российской
Федерации}
-города Российской Федерации.

21.

ПРЕДИКАТЫ
Для предикатов характерны
К примеру, система уравнений есть
те же действия, что и для конъюнкция предикатов:
высказываний, а именно:
х-1=5;
Р1(х)=х-1=5;
х =36;
Р2(х)=х =36;
Конъюнкция
Р1(х) ∧Р2(х)=6;
х=6;
(х-1=5)∧ (х =36);
х=-6;
Дизъюнкция
(х=6) ∧((х=-6 )ν(х=6));
х=6;
х=6
х=6
Импликация
Эквиваленция и др.
Ответ: {6}
2
2
2

22. Кванторы

Одним из способов получения высказываний из
предикатов является навешивание кванторов.
Для этого перед предикатом пишут кванторы –
слова, описывающие его множество истинности.
Квантор
всеобщности
Квантор
существования

23. квантор существования « ∃»

Квантор существования — это символ,
обозначающий единственное существование и
читается как «существует» или «для некоторого».
Из предиката {Студент 15-й группы
сдал тест по математике на 100 баллов }
получаются высказывание:
{Найдется такой студент в 15-й группе ,
который сдаст тест по математике на 100
баллов}

24. квантор всеобщности «∀»

Квантор всеобщности — это символ,
обозначающий всеобщность и читается как «для
любого» или «для всех».
Из предиката {Студент 15-й группы сдал
тест по математике на 100 баллов }
получаются высказывание:
{Все студенты 15-й группы сдали тест по
математике на 100 баллов}

25. Заключение

Таким образом, мы познакомились
с основными понятиями алгебры
логики, научились выполнять
операции с высказываниями,
определенными и
неопределёнными.
Надеемся, эта презентация
поможет Вам окунуться в мир
логики и абстрактного мышления.

26. Использованная литература

Шабунин М.И. Математика. Алгебра. Начала анализа.
http://ru.wikipedia.org