Элементы математической логики

1. Элементы математической логики

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ
ЛОГИКИ
В толковом словаре Ожегова С.И.
сказано: "Логика наука о законах
мышления и его формах".

2. Историческая справка:

ИСТОРИЧЕСКАЯ СПРАВКА:
Математическая
логика
–
раздел
математики,
изучающий
математические
доказательства
и
вопросы оснований математики.
Логика как наука
сформировалась в 4 в. до
н.э. Ее создал греческий
ученый Аристотель.
Слово «логика»
происходит от греческого
"логос", что с одной
стороны означает "слово"
или "изложение", а с
другой мышление.

3.

В 17 в. немецкий ученый
Лейбниц задумал создать
новую науку, которая была
бы «искусством исчисления
истины». В этой логике, по
мысли Лейбница, каждому
высказыванию соответствовал
бы символ, а рассуждения
имели бы вид вычислений.
Эта идея Лейбница, не
встретив понимания
современников, не получила
распространения и развития.

4.

Только
в середине 19 в. ирландский
математик Джордж Буль воплотил идею
Лейбница. В 1854 году им была
написана работа "Исследование законов
мышления", которая заложила основы
алгебры логики, в которой действуют
законы, схожие с законами обычной
алгебры, но буквами обозначаются не
числа, а высказывания.

5.

На языке булевой алгебры
можно описать рассуждения и
"вычислить" их результаты.
Однако ею охватываются
далеко не все рассуждения, а
лишь определенный тип
их, поэтому алгебру Буля
считают исчислением
высказываний.

6. АЛГЕБРА ВЫСКАЗЫВАНИЙ

Основными
понятиями
логики
высказываний являются высказывания
и логические связки (операции над
высказываниями).
В логике предикатов используются еще
предикаты и кванторы.

7. Кванторы

КВАНТОРЫ
Одним из способов получения высказываний из
предикатов является навешивание кванторов.
Для этого перед предикатом пишут кванторы –
слова, описывающие его множество истинности.
Квантор
всеобщности
Квантор
существования

8. квантор существования « ∃»

КВАНТОР СУЩЕСТВОВАНИЯ « ∃»
Квантор существования — это символ,
обозначающий единственное существование и
читается как «существует» или «для некоторого».
Из предиката {Ученик X Лицея города
Тюмени сдал ЕГЭ по математике более
чем на 70 баллов } получаются
высказывание:
{Найдется такой ученик Лицея города
Тюмени, который сдаст ЕГЭ по
математике более чем на 70 баллов}

9. квантор всеобщности «∀»

КВАНТОР ВСЕОБЩНОСТИ «∀»
Квантор всеобщности — это символ,
обозначающий всеобщность и читается как «для
любого» или «для всех».
Из предиката {Ученик X Лицея сдал ЕГЭ по
математике более чем на 70 баллов }
получаются высказывание:
{Все ученики Лицея сдали ЕГЭ по
математике более чем на 70 баллов}

10.

Высказывания и не
только в нашей
жизни…

11. МЫШЛЕНИЕ осуществляется через:

МЫШЛЕНИЕ
ОСУЩЕСТВЛЯЕТСЯ ЧЕРЕЗ:
Понятия
Высказывания
Умозаключения

12. ВЫСКАЗЫВАНИЕ

формулировка своего понимания
окружающего мира
(повествовательное предложение в
котором что-либо утверждается или
отрицается)
(Пример: Париж – столица Франции)

13. ВЫСКАЗЫВАНИЕ

ИСТИННОЕ
(Пример: Буква «А» гласная)
ЛОЖНОЕ
(Пример: Компьютер
был изобретен до
нашей эры)

14. УМОЗАКЛЮЧЕНИЕ

форма мышления, с помощью которой
из одного или нескольких суждений
может быть получено новое
суждение
(знание или вывод)
(Пример: любая теорема)

15.

Вопросительные,
повелительные
и
бессмысленные предложения не являются
логическими высказываниями.
По аналогии с элементарной алгеброй, где
любое
число
является
константой,
высказывание
является
логической
константой, величина которой равна 1 или 0.

16. Пример:

ПРИМЕР:
предложение « 2x = 4» не является
высказыванием. Для того чтобы имело смысл
говорить об его истинности или ложности,
необходимы
некоторые
дополнительные
сведения. Конечно, достаточно знать, какое
именно число обозначено буквой x.
Каждому
значению переменной x будет
соответствовать либо истинное, либо ложное
высказывание;
например,
при
х=2
высказывание истинно, при остальных ложно.

17. Операции над высказываниями

ОПЕРАЦИИ НАД ВЫСКАЗЫВАНИЯМИ
В логике над высказываниями производятся
следующие основные операции (логические
связки): отрицание, конъюнкция, дизъюнкция,
импликация,
эквиваленция,
неравнозначность. Они рассматриваются как
средство вычисления логического значения
сложного
высказывания
по
логическим
значениям
составляющих
его
простых
высказываний.

18. Отрицание (логическая связка «не»)

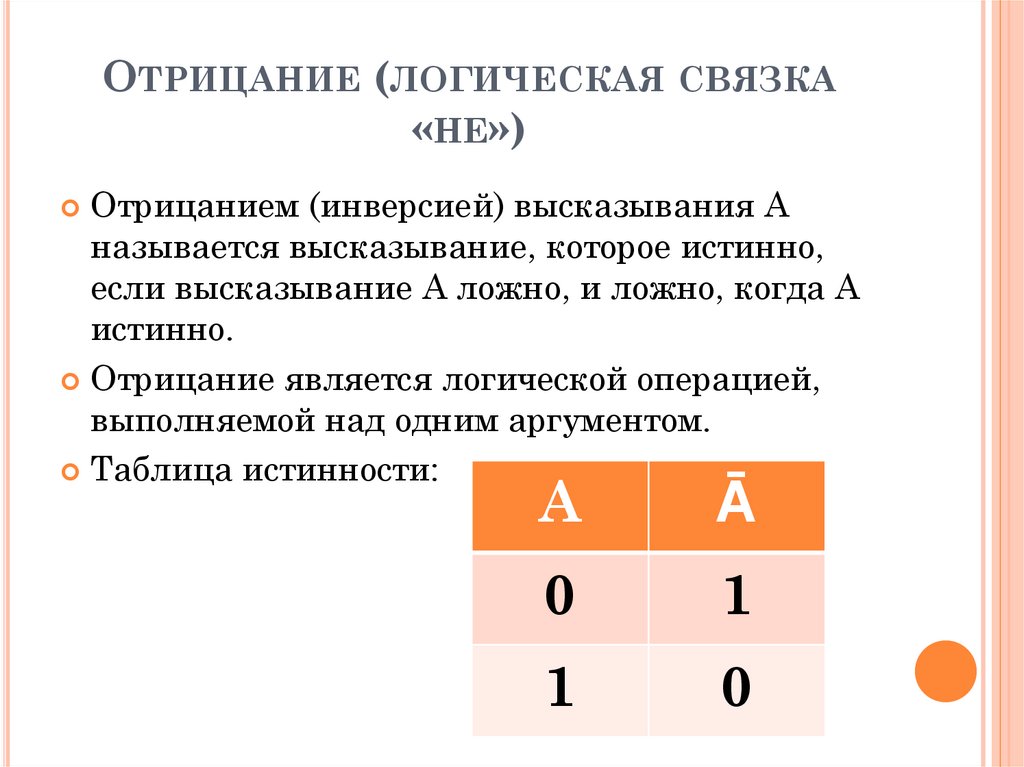
ОТРИЦАНИЕ (ЛОГИЧЕСКАЯ СВЯЗКА
«НЕ»)
Отрицанием (инверсией) высказывания A
называется высказывание, которое истинно,
если высказывание A ложно, и ложно, когда A
истинно.
Отрицание является логической операцией,
выполняемой над одним аргументом.
Таблица истинности:
А
Ā
0
1
1
0

19. Логическое умножение (конъюнкция)

ЛОГИЧЕСКОЕ УМНОЖЕНИЕ
(КОНЪЮНКЦИЯ)
Конъюнкция двух высказываний A и B — это
сложное логическое высказывание, которое
истинно только в случае истинности всех
составляющих высказываний, в противном
случае оно ложно. Обозначения: A & B, A ∧ B .
Читается: « A и B».
А
В
А^В
0
0
0
0
1
0
1
0
0
1
1
1

20. Логическое сложение (дизъюнкция)

ЛОГИЧЕСКОЕ СЛОЖЕНИЕ
(ДИЗЪЮНКЦИЯ)
Дизъюнкция двух высказываний A
и B — это сложное логическое
высказывание, которое ложно
только в случае ложности всех
составляющих высказываний, в
противном случае оно истинно.
Высказывание считается
истинным, когда истинно хотя бы
одно из составляющих
высказываний.
Обозначается: A ∨ B , A + B.
Читается: « A или B».
А
В
АvВ
0
0
1
1
0
1
0
1
0
1
1
1

21. Логическое следование (импликация)

ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ
(ИМПЛИКАЦИЯ)
В математических доказательствах часто
пользуются сложными высказываниями,
образованными с помощью слов «если…, то…».
Здесь высказывание, расположенное после
слова «если», называется основанием
(посылкой), а высказывание, расположенное
после слова «то», называется следствием или
заключением.
Импликацией двух высказываний A и B
называется высказывание, обозначаемое
символом A →B (A ⊃ B), которое ложно тогда и
только тогда, когда A истинно, а B ложно.
Читается: «если A, то B» (« A влечет B», «из A
следует B»).

22. Таблица истинности для импликации

ТАБЛИЦА ИСТИННОСТИ ДЛЯ
ИМПЛИКАЦИИ
А
В
А→В
0
0
1
0
1
1
1
0
0
1
1
1

23. Пример:

ПРИМЕР:
Определение импликации вынуждает считать
истинными такие предложения, как:
«Если 2×2=4, то Москва столица
России».
Это связано с тем, что определениями
логических операций смысл составляющих
высказываний
не
учитывается,
они
рассматриваются как объекты, обладающие
единственным свойством — быть истинными,
либо ложными.

24. Логическое тождество (эквиваленция)

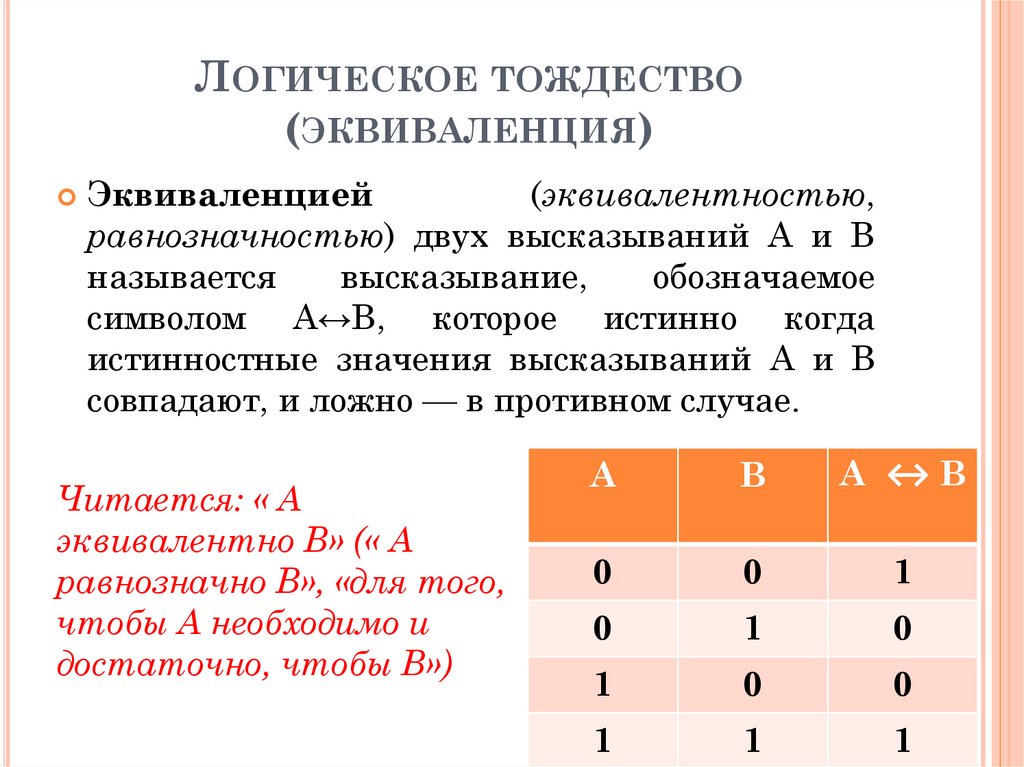
ЛОГИЧЕСКОЕ ТОЖДЕСТВО
(ЭКВИВАЛЕНЦИЯ)
Эквиваленцией
(эквивалентностью,
равнозначностью) двух высказываний A и B
называется
высказывание,
обозначаемое
символом A↔B, которое истинно когда
истинностные значения высказываний A и B
совпадают, и ложно — в противном случае.
Читается: « A
эквивалентно B» (« A
равнозначно B», «для того,
чтобы A необходимо и
достаточно, чтобы B»)
А
В
А ↔В
0
0
1
0
1
0
1
0
0
1
1
1

25. Исключающее «или» (неравнозначность)

ИСКЛЮЧАЮЩЕЕ «ИЛИ»
(НЕРАВНОЗНАЧНОСТЬ)
Неравнозначностью двух высказываний A и B
называется высказывание, истинное, когда
истинностные значения A и B не совпадают, и
ложное — в противном случае.
Обозначается: A⊕ B .
Читается: «либо A, либо B»
А
В
А ⊕В
0
0
0
0
1
1
1
0
1
1
1
0

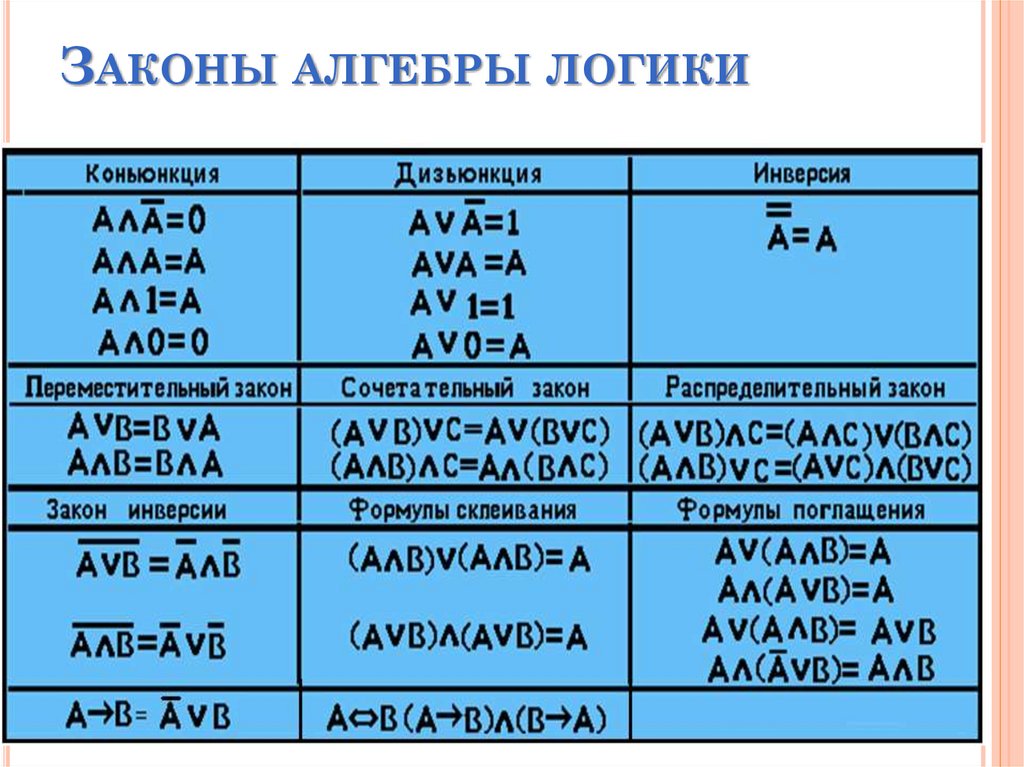
26. Законы алгебры логики

ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

27.

ПРЕДИКАТЫ
Для предикатов характерны
те же действия, что и для
высказываний, а именно:
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция и др.
К примеру, система уравнений
есть конъюнкция предикатов:
х-1=5;
х2=36;
х=6;
х=-6;
х=6;
х=6
Р1(х)=х-1=5;
Р2(х)=х2=36;
Р1(х) ∧Р2(х)=6;
(х-1=5)∧ (х2=36);
(х=6) ∧((х=-6 )ν(х=6));
х=6
Ответ: {6}

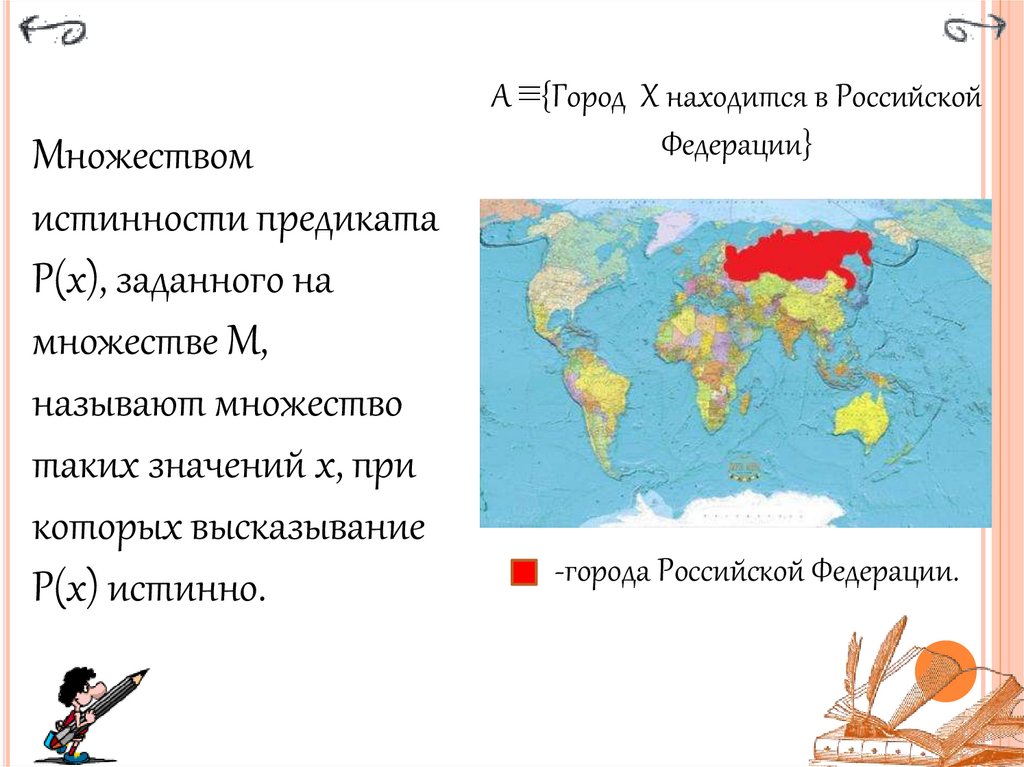
28.

Множеством
истинности предиката
Р(х), заданного на
множестве М,
называют множество
таких значений х, при
которых высказывание
Р(х) истинно.
A ≡{Город Х находится в Российской
Федерации}
-города Российской Федерации.

29. Решение задач

РЕШЕНИЕ ЗАДАЧ

30. Задача №1

ЗАДАЧА №1
задания
Для какого числа X истинно высказывание:
((x<4)→(x<3))^((x<3)→(x<1))
1)1 2)2 3)3 4)4
Решение:
Подставляем в выражение предложенные варианты ответа и определяем,
истинно выражение или ложно:
1) x=1: ((1<4)→(1<3))^((1<3)→(1<1))=(1→1)^(1→0)
Сначала вычислим выражение в скобках:
(1→1)^(1→0)=1^0=0 (не подходит)
Аналогично подставляем другие варианты ответа, вычисляем:
2) x=2: ((2<4)→(2<3))^((2<3)→(2<1))=(1→1)^(1→0)=1^0=0 (не подходит)
3) x=3: ((3<4)→(3<3))^((3<3)→(3<1))=(1→0)^(0→0)=0^1=0
(не подходит)
4) x=4: ((4<4)→(4<3))^((4<3)→(4<1))=(0→0)^(0→0)=1^1=1
(подходит)
Ответ: 4.

31. Задача №2

ЗАДАЧА №2
задания
Для какого имени ложно высказывание:
(первая буква гласная ^последняя буква
согласная)→ ¬(третья буква согласная)?
1)
Дмитрий 2) Антон 3) Екатерина 4) Анатолий
Решение:
Подставляем в выражение предложенные варианты ответа и
определяем, истинно выражение или ложно:
1)
Дмитрий: (0 ^ 1)→ ¬(0)=0→1 = 1 (не подходит)
2)
Антон:
(1 ^ 1)→ ¬(1)=1→0 = 0 (подходит)
3)
Екатерина: (1 ^ 0)→ ¬(0)=0→1 = 1 ( не подходит)
4)
Анатолий: (1 ^ 1)→ ¬(0)=1→1 = 1 ( не подходит)
Ответ: 2.

32. Задача №3

ЗАДАЧА №3
задания
Построить таблицу истинности для следующей функции:
F(X,Y,Z)=(x→y)·z + ¬y
Решение:
1) Нарисуем таблицу на K строк, где K=2n, n - количество
высказываний в функции
N=3, k=8 строк
2) Запишем в таблице все варианты X,Y,Z и вычисляем выражение
по
действиям:

33. Задача №4

задания
ЗАДАЧА №4
Каково наименьшее натуральное число X, при котором
истинно высказывание
( x ( x 1) 99) (( x 1) ( x 1) 80)
Решение: Импликация ложна, когда первое выражение
истинно, а второе ложно(см. таблицы истинности). Во всех
остальных случаях импликация истинна. Первое
выражение ложно для всех натуральных x>10 и истинно
для всех натуральных x<11. Второе выражение истинно
для всех натуральных x>9 и ложно для всех натуральных
x<10. Следовательно, данная импликация истинна для
всех натуральных x>9. Наименьшее число,
соответствующее этому условию x=10.
Ответ: 10.

34. Задача №5

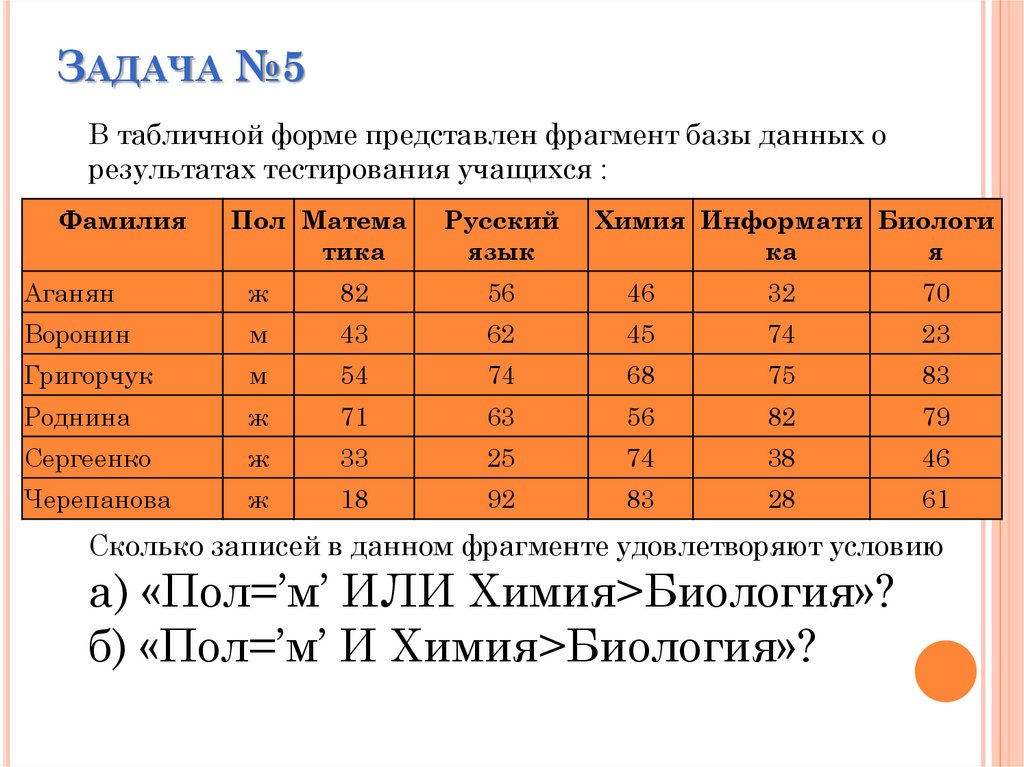
ЗАДАЧА №5
В табличной форме представлен фрагмент базы данных о
результатах тестирования учащихся :
Фамилия
Пол Матема
тика
Русский
язык
Химия Информати Биологи
ка
я
Аганян
ж
82
56
46
32
70
Воронин
м
43
62
45
74
23
Григорчук
м
54
74
68
75
83
Роднина
ж
71
63
56
82
79
Сергеенко
ж
33
25
74
38
46
Черепанова
ж
18
92
83
28
61
Сколько записей в данном фрагменте удовлетворяют условию
а) «Пол=’м’ ИЛИ Химия>Биология»?
б) «Пол=’м’ И Химия>Биология»?

35. Задача №5

задания
ЗАДАЧА №5
Фамилия
Пол Математ
ика
Русский
язык
Химия Информатик Биология
а
Аганян
ж
82
56
46
32
70
Воронин
м
43
62
45
74
23
Григорчук
м
54
74
68
75
83
Роднина
ж
71
63
56
82
79
Сергеенко
ж
33
25
74
38
46
Черепанова
ж
18
92
83
28
61
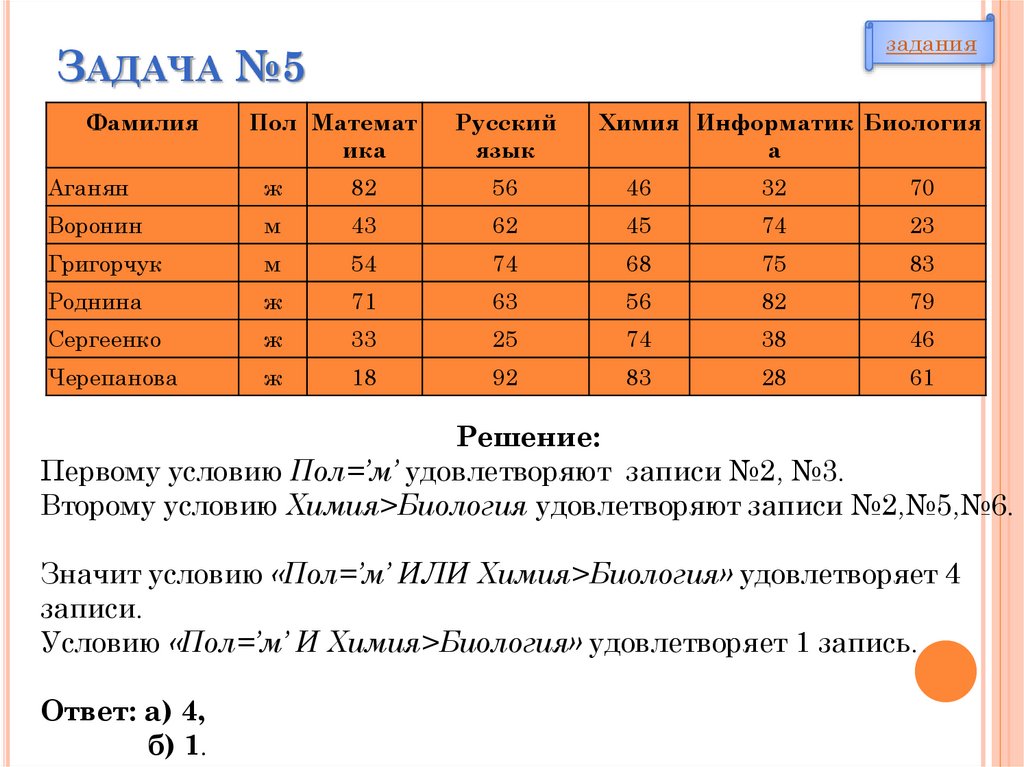
Решение:
Первому условию Пол=’м’ удовлетворяют записи №2, №3.
Второму условию Химия>Биология удовлетворяют записи №2,№5,№6.
Значит условию «Пол=’м’ ИЛИ Химия>Биология» удовлетворяет 4
записи.
Условию «Пол=’м’ И Химия>Биология» удовлетворяет 1 запись.
Ответ: а) 4,
б) 1.