Similar presentations:
Основы математического анализа
1.
Основыматематического
анализа
Зарубежное регионоведение
1 курс
Сафонова Татьяна Евгеньевна, к.ф.-м.н., доцент
2. План курса
• Основы математической логики и теориимножеств
• Матрицы и определители
• Системы линейных алгебраических
уравнений (СЛАУ)
• Формализация бинарных отношений и
двухместных предикатов в виде графов
2
3. Элементы математической логики
4. Высказывания
• Высказывание – всякое утверждение, окотором объективно и определенно можно
сказать, истинно оно или ложно.
Например:
• «параллелограмм имеет четыре вершины»,
• «число 25 делится на 5»,
• «зимой день короче, чем летом».
5. Обозначения
• Высказываниябудем
обозначать
большими латинскими буквами
• фиксированные высказывания – А, В,
С, …, любые высказывания – X, Y, Z,
• значения истинности высказывания – 1
(истина) и 0 (ложь).
6. Формулы
• Пусть заданы высказывания X1, X2,…, Xn(их можно назвать исходными),
тогда из них с помощью символов логических
операций можно образовать выражения, или
формулы.
• Например, (X1 X2) X3,
((X1 X2) X3) (X1 X4) и т.п.
7. Операции над высказываниями
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
8. Приоритет операций
отрицание ( )
конъюнкция ( )
дизъюнкция ( )
импликация ( )
эквиваленция ( )
8
9. Отрицание
• Отрицанием А (обозначается А)называется высказывание А («не А»),
которое истинно, когда ложно А, и ложно,
когда А истинно.
А
А
1
0
0
1
10. Конъюнкция
• Конъюнкцией (от лат. conjunctio –союз, связь) высказываний А и В
называется высказывание А В
(«А и В»), истинное в том и только в том
случае, когда оба высказывания А и В
истинны.
11. Таблица истинности
AB
A B
0
0
0
1
0
0
0
1
0
1
1
1
12. Дизъюнкция
• Дизъюнкцией (от лат. disjunctio –различие) высказываний А и В
называется высказывание А В
(«А или В»), ложное в том и только в том
случае, когда оба высказывания А и В
ложны.
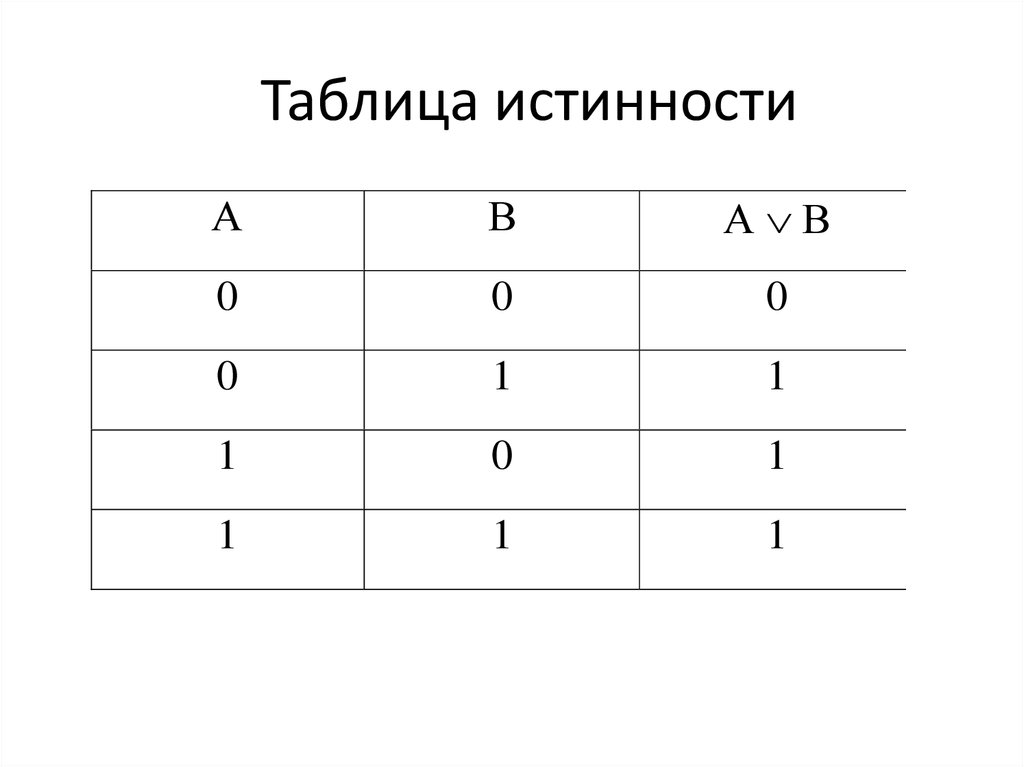
13. Таблица истинности
АВ
А В
0
0
0
0
1
1
1
0
1
1
1
1
14. Импликация
• Импликацией (от лат. implico – тесносвязаны) высказываний А и В называется
высказывание А В
(«А влечет В», «А имплицирует В», ложное в
том и только в том случае, когда А истинно, а
В ложно.
• Еще одно обозначение импликации: А В
(«если А, то В»).
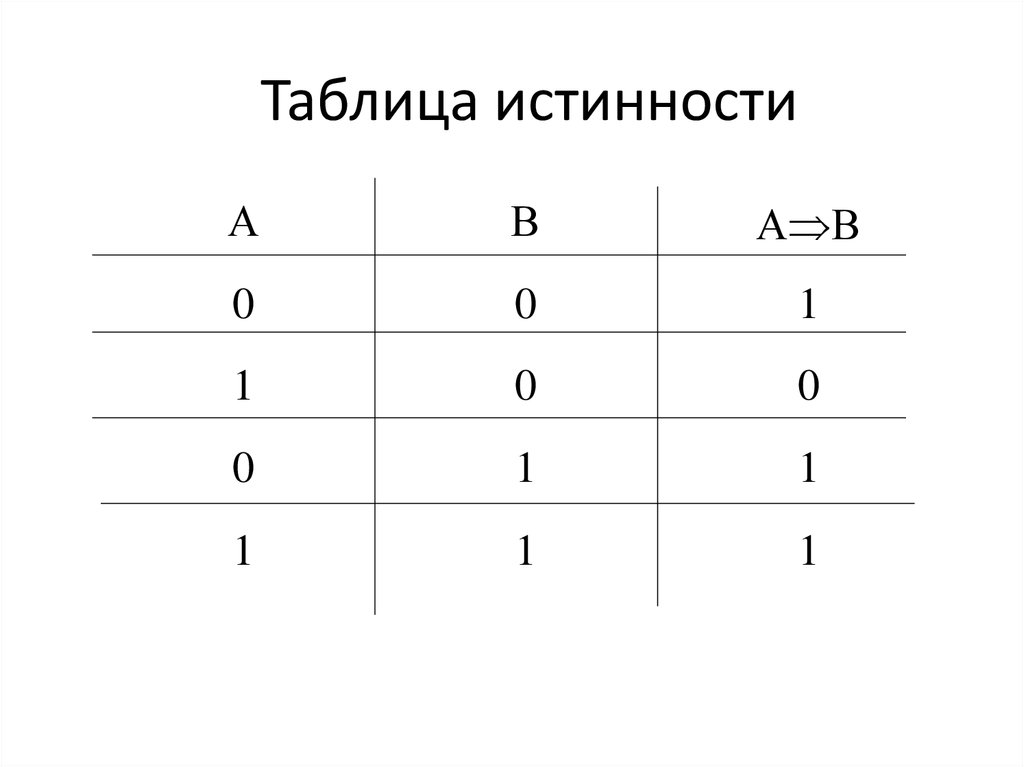
15. Таблица истинности
АВ
А В
0
0
1
1
0
0
0
1
1
1
1
1
16. Эквиваленция
• Эквиваленцией высказываний А и Вназывается высказывание А В
(«А эквивалентно В», «эквиваленция А и В»,
истинное в том и только в том случае, когда
высказывания А и В оба истинны или оба
ложны.
• Еще одно обозначение: А ~ В («А тогда и
только тогда, когда В»).
17. Таблица истинности
АВ
А В
0
0
1
1
0
0
0
1
0
1
1
1
18. ТИ и ТЛ
• Формула A (X1, …, Xn), принимающая для всехзначений из Bn значение 1, называется
тождественно истинным (ТИ-)
высказыванием, а формула, принимающая
для всех значений из Bn значение 0 –
тождественно ложным (ТЛ-)
высказыванием.
19. Логические законы
• Тождественно истинные высказываниязаписывают законы, так как они
истинны только в силу своей формы,
независимо от содержания исходных
высказываний.
19
20. Примеры законов
• X X• X X
• X X
закон тождества
закон исключенного третьего
закон противоречия
20
21.
• Формулы A и B называютсяэквивалентными (равносильными),
если высказывание A B является
ТИ-высказыванием.
22. Пример решения задачи 1
• Доказать логический закон, используятаблицы истинности:
(Х У) Х У
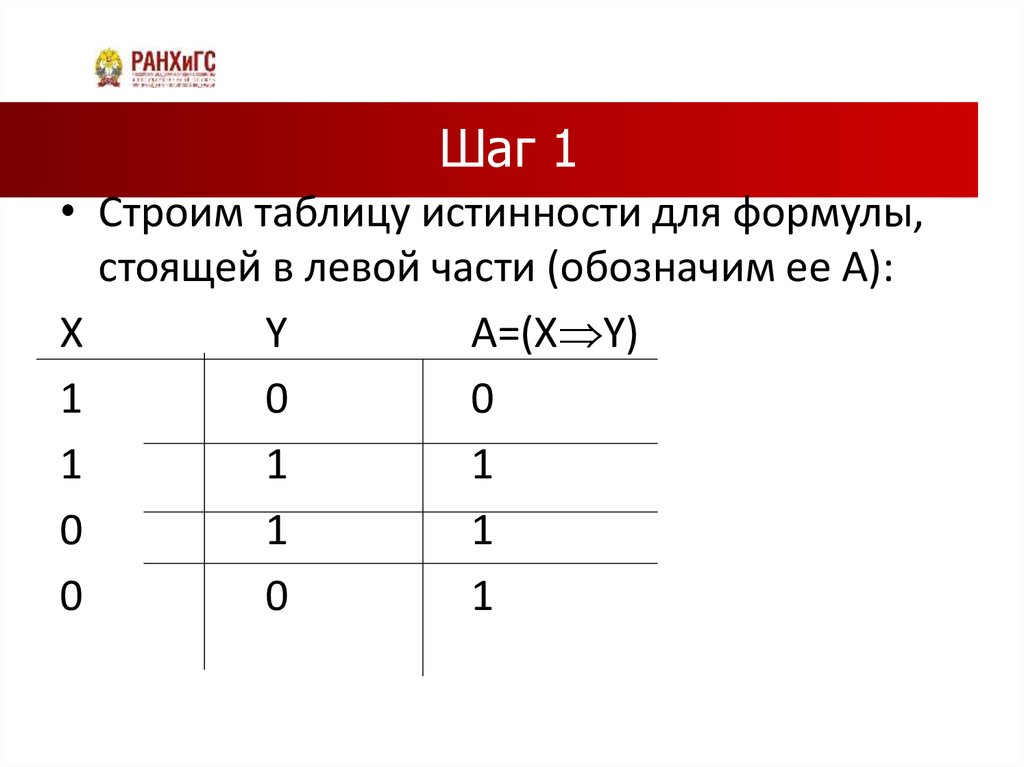
23. Шаг 1
• Строим таблицу истинности для формулы,стоящей в левой части (обозначим ее А):
Х
Y
А=(Х Y)
1
0
0
1
1
1
0
1
1
0
0
1
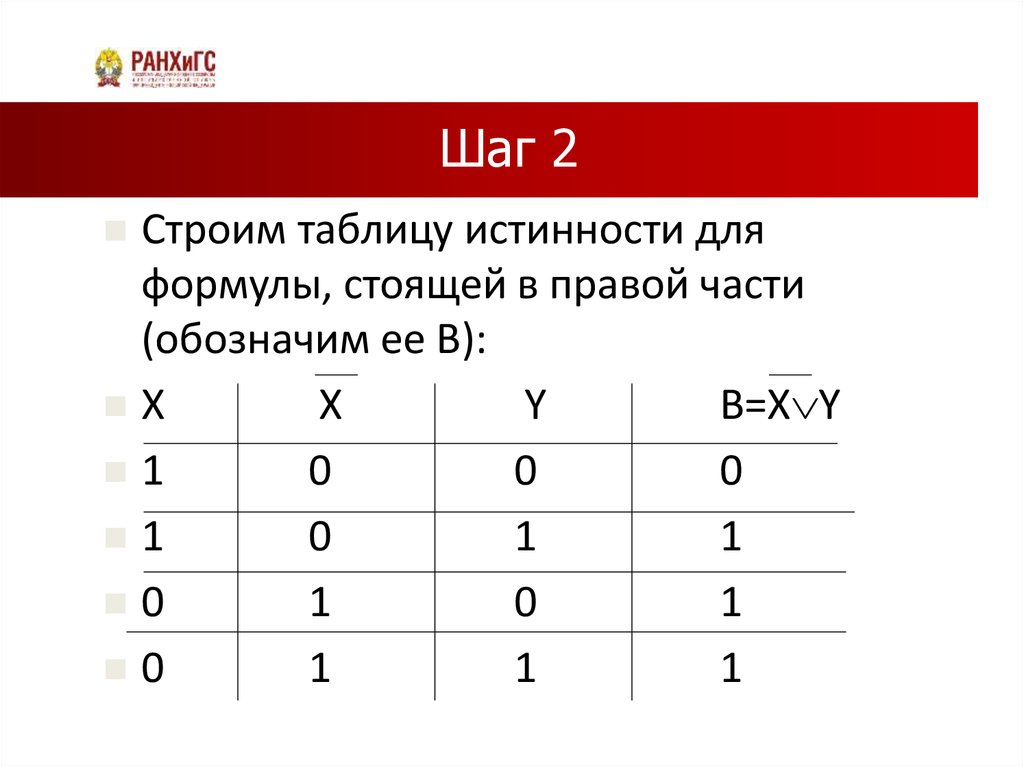
24. Шаг 2
Строим таблицу истинности дляформулы, стоящей в правой части
(обозначим ее В):
Х
Х
Y
В=Х Y
1
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
25. Шаг 3
• Строим таблицу истинности для формулыА В:
Х
Y
А
В
А В
1
0
0
0
1
1
1
1
1
1
0
1
1
1
1
0
0
1
1
1
26. Шаг 4
• Поскольку формула А В являетсятождественно истинной, закон доказан.
27. Предикат
• В каждом высказывании есть подлежащееи сказуемое, т.е. объект и предикат
(свойство объекта).
• Множество объектов, для которых может
быть определен данный предикат,
образуют поле предиката М.
27
28.
• предикат – это функция Р(х), определеннаяна М со значениями «истина» или «ложь».
28
29.
• Если в предложении содержится утверждениео нескольких объектах и отношениях между
ними, то оно может быть записано с
использованием многоместного предиката.
• Например, высказывание «3 > 0» («3 больше
0») может быть формализовано не только с
помощью одноместного предиката Р(х)
(«х > 0»), но и двухместного предиката Р(х, у)
(«х > y»).
29
30. Кванторы
• Для того, чтобы характеризовать свойстване каждого отдельного объекта, а всей их
совокупности (всего поля предиката),
используются кванторы.
• квантор общности (обозначается ) и
квантор существования (обозначается )
30
31.
• Переход от P(x) к xP(x) называетсянавешиванием квантора общности по
предметной переменной x.
• При этом переходе предикату P(x) ставится
в соответствие высказывание xP(x)
(читается: «для всякого x имеет место
P(x)»), которое по определению является
истинным тогда и только тогда,
когда высказывание P(a) истинно для
любого a M.
31
32.
• Переход от P(x) к xP(x) называетсянавешиванием квантора существования по
предметной переменной x.
• При этом переходе предикату P(x) ставится в
соответствие высказывание xP(x)
• (читается: «существует такое x, что имеет
место P(x)»), которое по определению
является истинным тогда и только тогда, когда
высказывание P(a) истинно хотя бы для
одного a M.
32
33. Пример
• Определим на множестве N предикат P,полагая P(a)=1 тогда и только тогда, когда a
– простое.
• Тогда xP(x) есть высказывание «всякое
натуральное число является простым»
(ложное),
• xP(x) – «существует натуральное число,
являющееся простым» (истинное).
33
34. Элементы теории множеств
35. Множество
• Множество — совокупность определенныхразличаемых объектов таких, что для
любого объекта можно установить,
принадлежит этот объект данному
множеству или нет.
• Множества обозначаются прописными
буквами: A, B, C ..., элементы – строчными
буквами: x, y, z, …
36. Задание множеств
• перечисление всех элементов множестваA= {7, 8, 9}
• указание свойств элементов множества
A={x: x — целое число и 6 < x < 10}
• x A
• x A
37. Операции над множествами
пересечение
объединение
разность
симметрическая разность
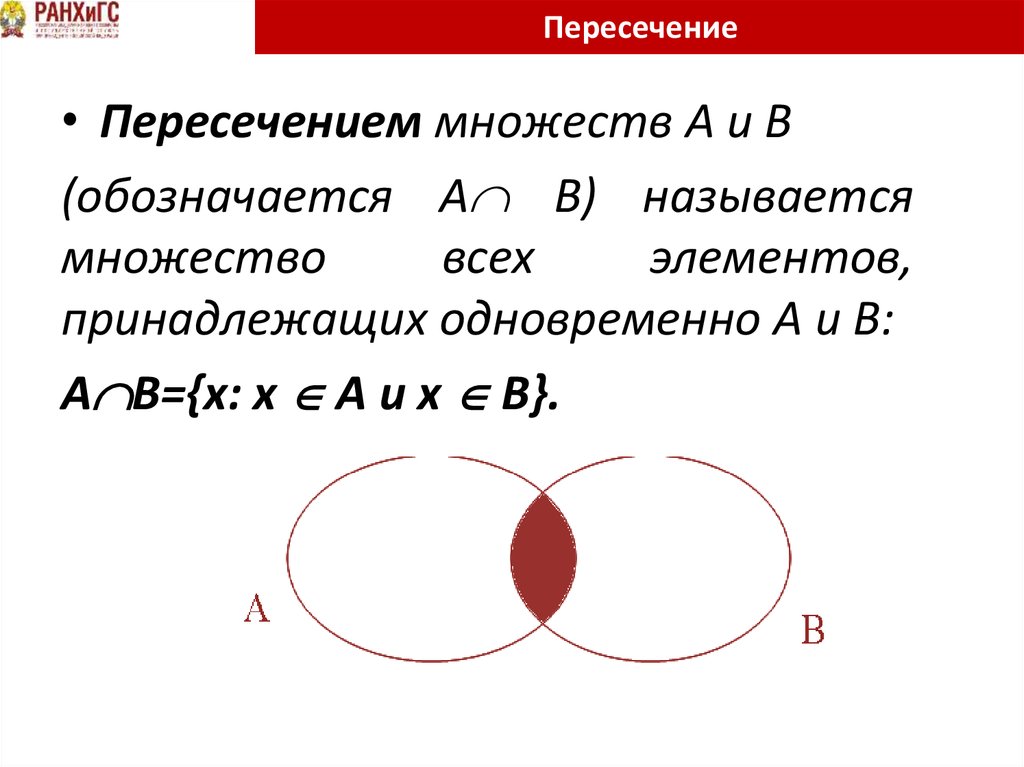
38. Пересечение
• Пересечением множеств A и B(обозначается A B) называется
множество
всех
элементов,
принадлежащих одновременно A и B:
A B={x: x A и x B}.
39. Объединение
• Объединением множеств A и B(обозначается A B) называется
множество
всех
элементов,
принадлежащих либо A, либо B,
либо одновременно и A и B:
A B={x: x A или x B}.
40. Разность
• Разность (дополнение) множеств A и B(записывается в виде A \ B) — множество
элементов, принадлежащих A и не
принадлежащих B:
A \ B ={x: x A и x B} (дополнение B до A).
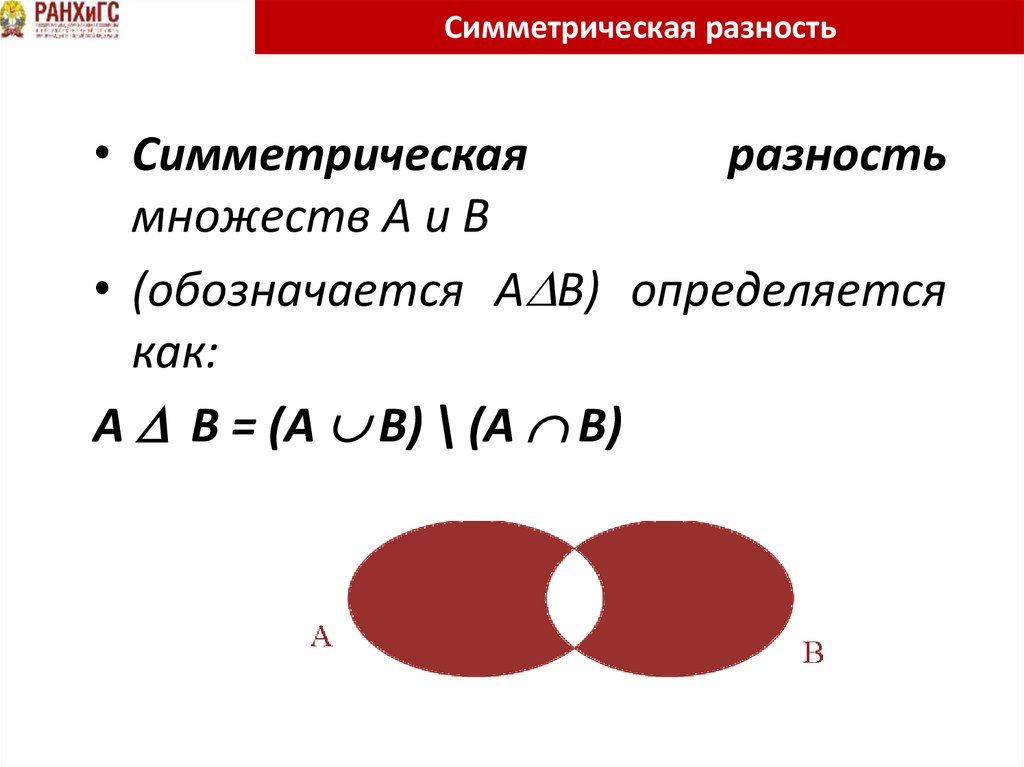
41. Симметрическая разность
• Симметрическаяразность
множеств A и B
• (обозначается A B) определяется
как:
A B = (A B) \ (A B)
42.
• Пустое множество (обозначается )есть множество, обладающее свойством:
x при любом x.
• Универсальное множество (обозначается
E) есть множество всех рассматриваемых в
данной задаче элементов.
43. Дополнение
• Дополнение множества A(обозначается A ) определяется как
A = E \ A = {x: x A}.






































 mathematics
mathematics








