Similar presentations:
Альтернативные методы решения планиметрических задач. Трапеция
1.
2.
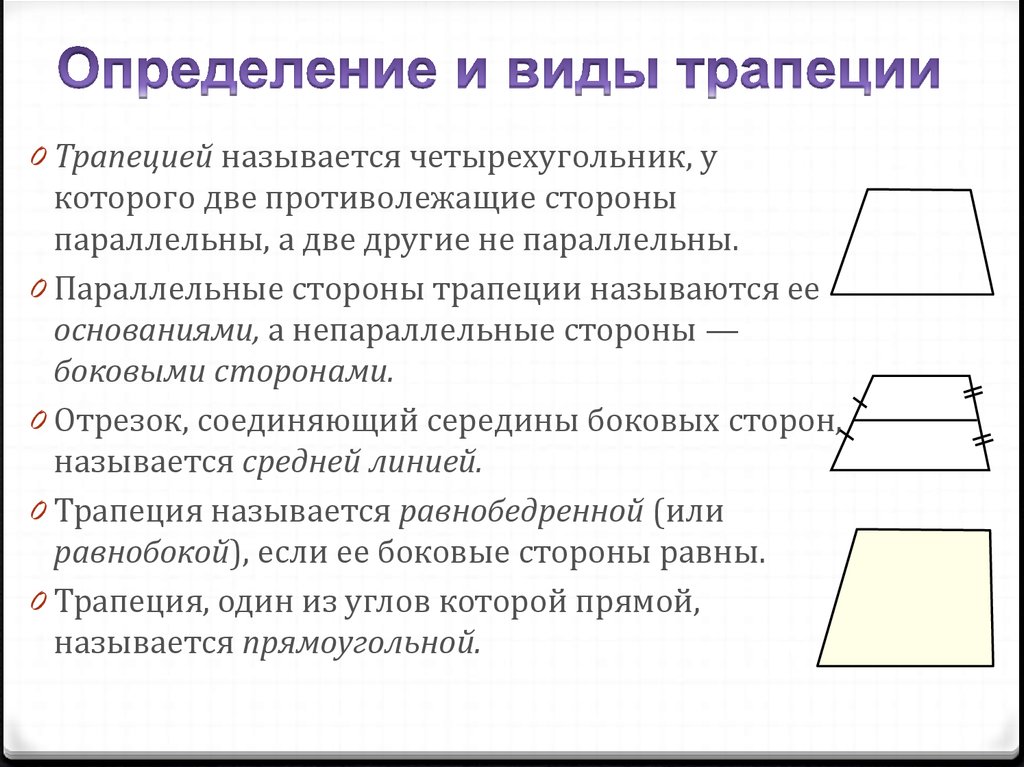
0 Трапецией называется четырехугольник, укоторого две противолежащие стороны
параллельны, а две другие не параллельны.
0 Параллельные стороны трапеции называются ее
основаниями, а непараллельные стороны —
боковыми сторонами.
0 Отрезок, соединяющий середины боковых сторон,
называется средней линией.
0 Трапеция называется равнобедренной (или
равнобокой), если ее боковые стороны равны.
0 Трапеция, один из углов которой прямой,
называется прямоугольной.
3.
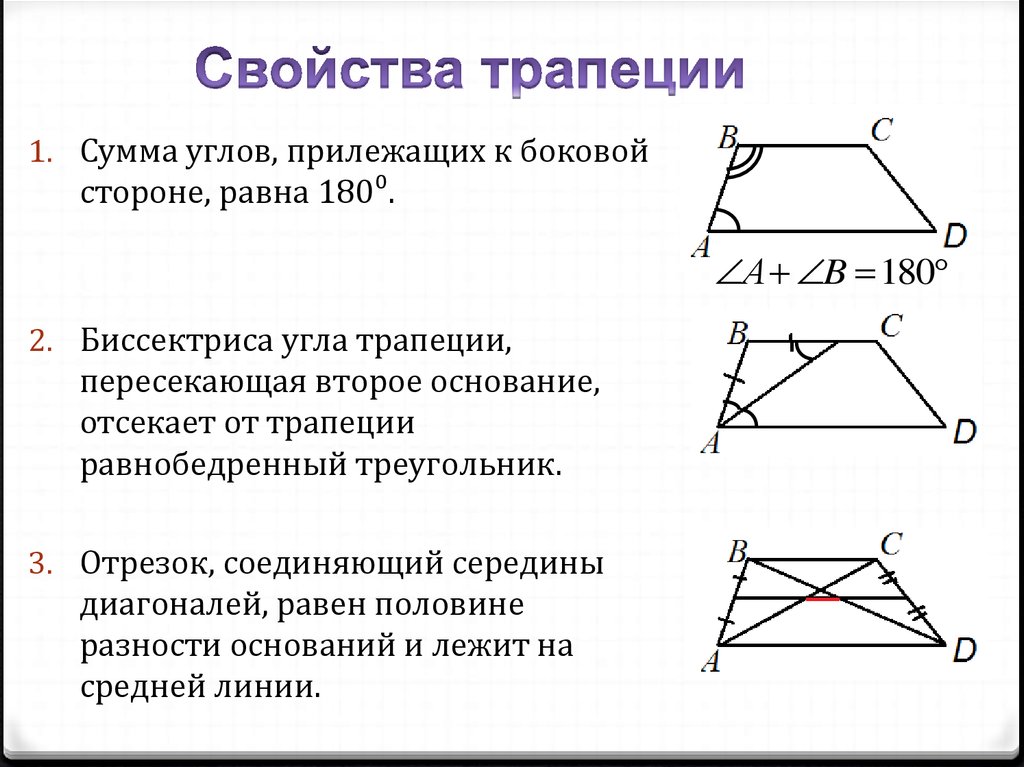
1. Сумма углов, прилежащих к боковойстороне, равна 180⁰.
А B 180
2. Биссектриса угла трапеции,
пересекающая второе основание,
отсекает от трапеции
равнобедренный треугольник.
3. Отрезок, соединяющий середины
диагоналей, равен половине
разности оснований и лежит на
средней линии.
4.
4. Средняя линия трапеции делитлюбой отрезок с концами, лежащими
на прямых, содержащих основания,
пополам.
5. В трапецию можно вписать
окружность, если сумма оснований
трапеции равна сумме её боковых
AB CD BC AD
сторон.
N
6. Если сумма углов при любом
основании трапеции равна 90°, то
отрезок, соединяющий середины
М
оснований, равен их полуразности.
А D 90
AD BC
MN
2
5.
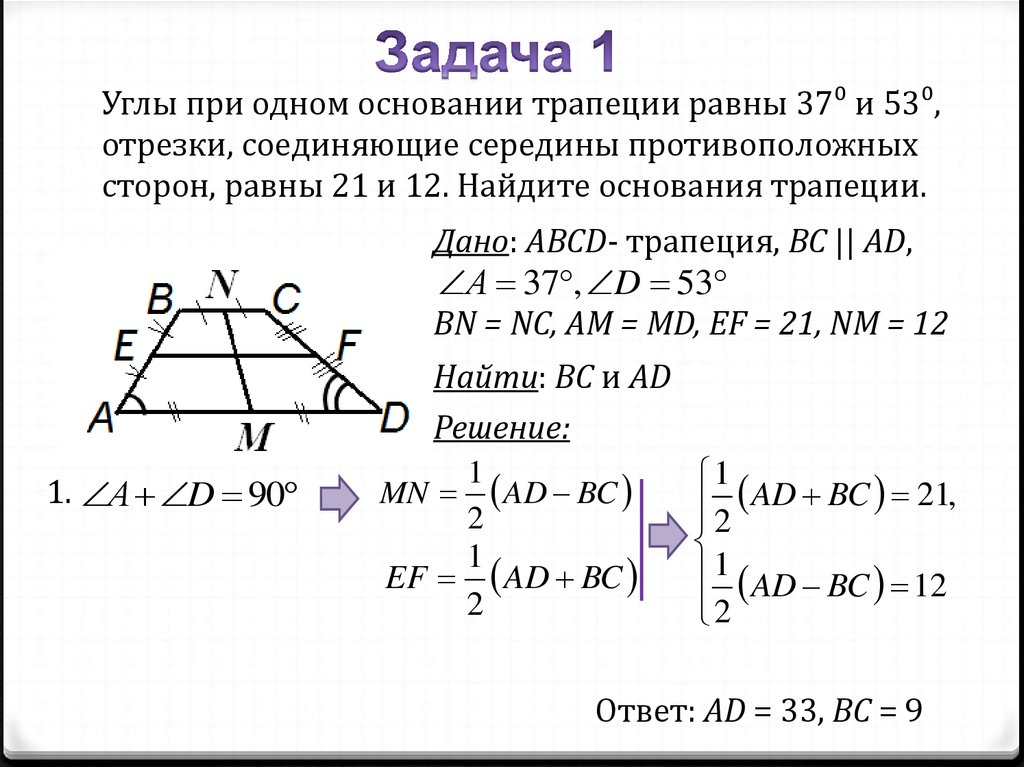
Углы при одном основании трапеции равны 37⁰ и 53⁰,отрезки, соединяющие середины противоположных
сторон, равны 21 и 12. Найдите основания трапеции.
Дано: ABCD- трапеция, BC || AD,
А 37 , D 53
BN = NC, AM = MD, EF = 21, NM = 12
Найти: BC и AD
Решение:
1. А D 90
1
MN AD BC
2
1
EF AD BC
2
1
2 AD BC 21,
1 AD BC 12
2
Ответ: AD = 33, BC = 9
6.
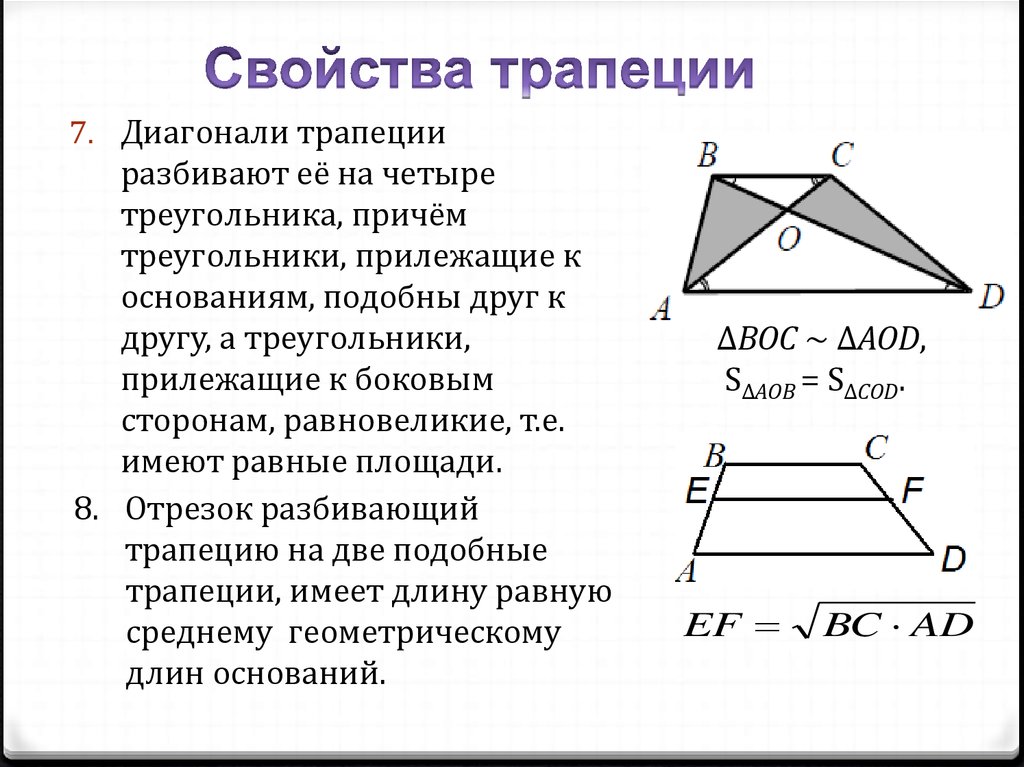
7. Диагонали трапецииразбивают её на четыре
треугольника, причём
треугольники, прилежащие к
основаниям, подобны друг к
другу, а треугольники,
прилежащие к боковым
сторонам, равновеликие, т.е.
имеют равные площади.
8. Отрезок разбивающий
трапецию на две подобные
трапеции, имеет длину равную
среднему геометрическому
длин оснований.
ΔВОС ~ ΔAOD,
SΔAOB = SΔCOD.
EF
BC AD
7.
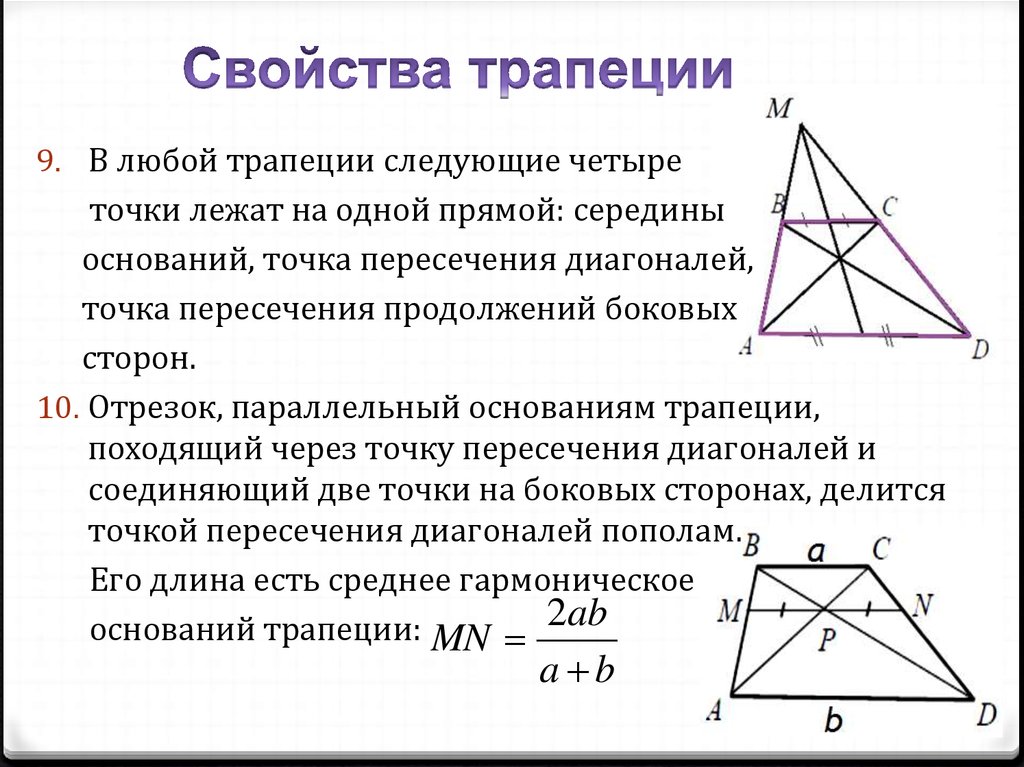
9. В любой трапеции следующие четыреточки лежат на одной прямой: середины
оснований, точка пересечения диагоналей,
точка пересечения продолжений боковых
сторон.
10. Отрезок, параллельный основаниям трапеции,
походящий через точку пересечения диагоналей и
соединяющий две точки на боковых сторонах, делится
точкой пересечения диагоналей пополам.
Его длина есть среднее гармоническое
оснований трапеции: MN 2ab
a b
8.
11. Если в трапецию вписана окружность,то отрезки, соединяющие центр
окружности с концами боковой стороны
трапеции, перпендикулярны.
r
ab
a 2 b2
,
12. Если в трапецию вписана окружность и m, n, p, q- длины
отрезков боковых сторон от точек касания до вершин,
то для вычисления радиуса вписанной в неё окружности
можно использовать формулы:
n
p
r mn pq .
m
q
9.
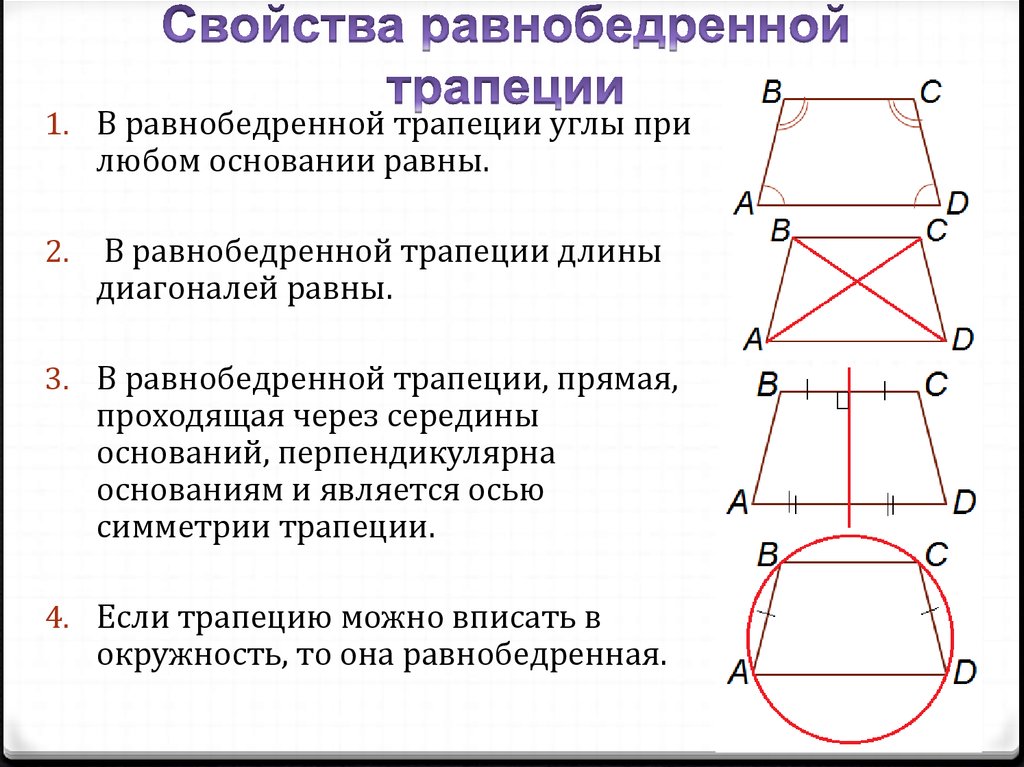
1. В равнобедренной трапеции углы прилюбом основании равны.
2.
В равнобедренной трапеции длины
диагоналей равны.
3. В равнобедренной трапеции, прямая,
проходящая через середины
оснований, перпендикулярна
основаниям и является осью
симметрии трапеции.
4. Если трапецию можно вписать в
окружность, то она равнобедренная.
10.
Найдите площадь равнобедренной трапеции, если еёдиагональ, равная 10, образует с основанием угол, косинус
2
которого равен
.
10
B
C
Дано: ABCD - трапеция, AD || BC
10
cos BDH = 2 , BD = 10
7 2
Найти: S 10
План решения: S = mh
A х
D
1) HD= 2 ;
х
К
2
H
2) ВН = 7 2 ;
BC AD
,
3) АН = KD = x, m
2
AD 2 x AD 2 AD 2 x
m
AD x HD 2
2
2
4) S = 2 7 2 14
Ответ: 14
11.
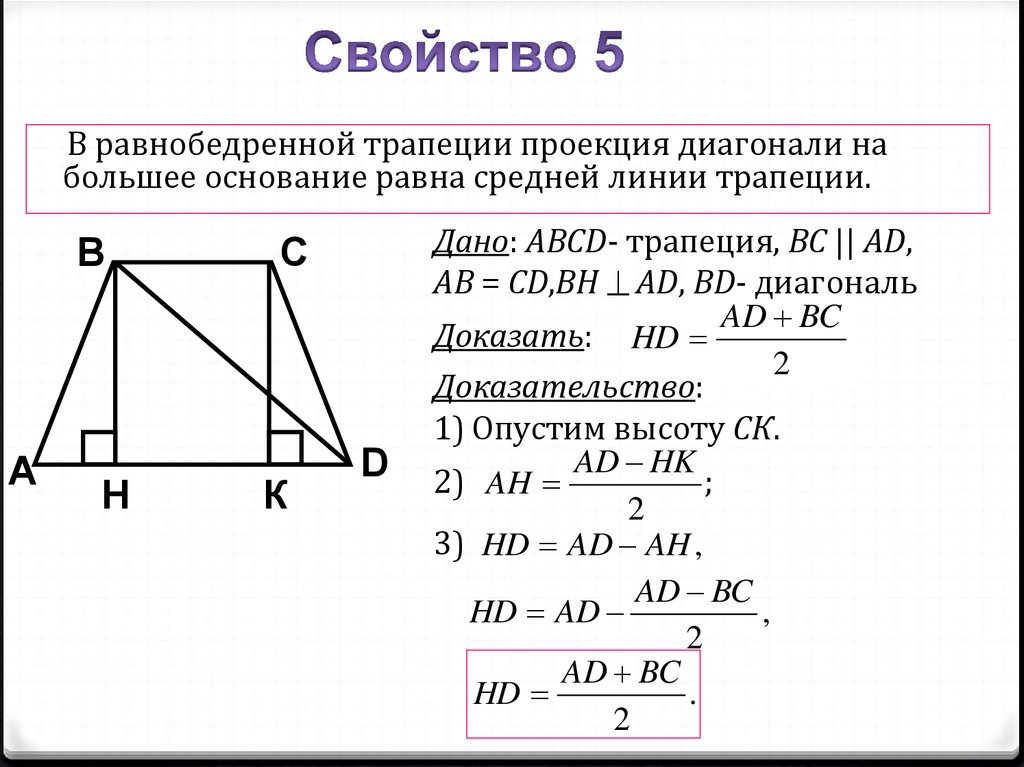
В равнобедренной трапеции проекция диагонали набольшее основание равна средней линии трапеции.
B
A
H
C
К
D
Дано: ABCD- трапеция, BC || AD,
AB = CD,ВН AD, BD- диагональ
AD BC
Доказать: HD
2
Доказательство:
1) Опустим высоту СК.
AD HK
2) AH
;
2
3) HD AD AH ,
AD BC
HD AD
,
2
AD BC
HD
.
2
12.
Найдите площадь равнобедренной трапеции, если еёдиагональ, равная 10, образует с основанием угол, косинус
которого равен 2 .
10
B
C
10
7 2
A
H
D
2
Дано: ABCD - трапеция,
AD || BC
2
cos BDH =
, BD = 10
10
Найти: S
План решения: S = mh
1) HD= 2 ;
2) ВН = 7 2 ;
3) S = 2 7 2 14
Ответ: 14
13.
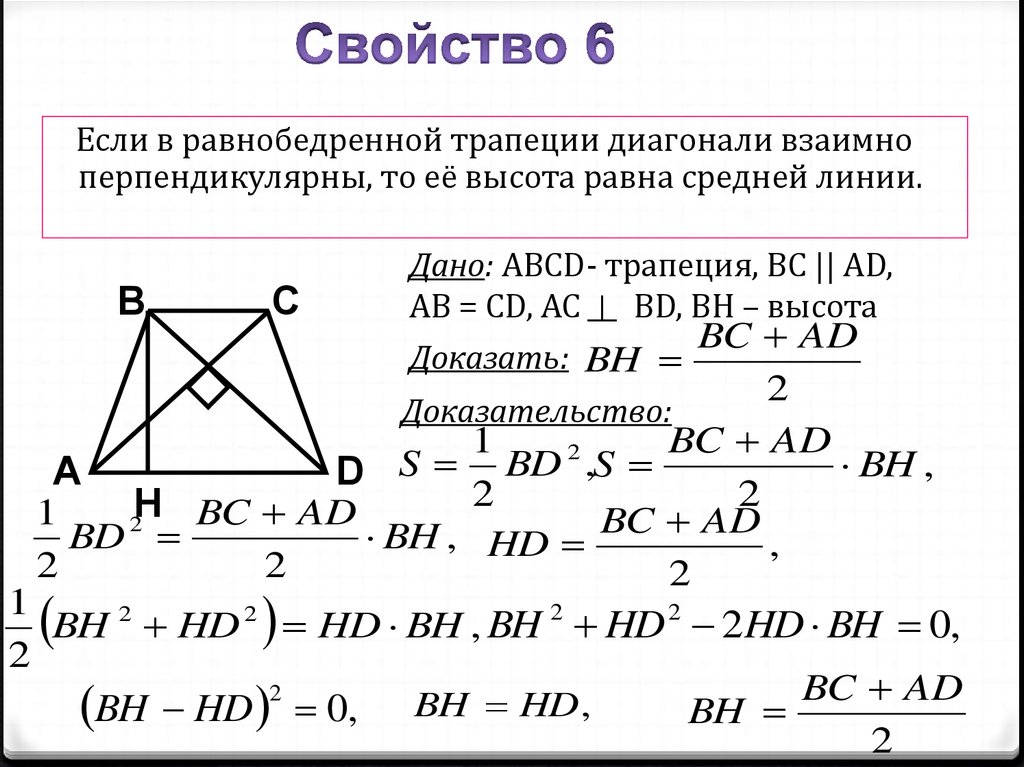
Если в равнобедренной трапеции диагонали взаимноперпендикулярны, то её высота равна средней линии.
B
С
Дано: ABCD- трапеция, BC || AD,
AB = CD, AC BD, BH – высота
BC AD
Доказать: BH
2
Доказательство:
1
BC AD
2
BH ,
A
D S BD ,S
2
2
Н
1
BC AD
2
BD
BH , HD BC AD ,
2
2
2
1
2
2
2
2
BH
HD
2 HD BH 0,
BH HD HD BH ,
2
BC AD
2
BH
HD
,
BH HD 0,
BH
2
14.
15.
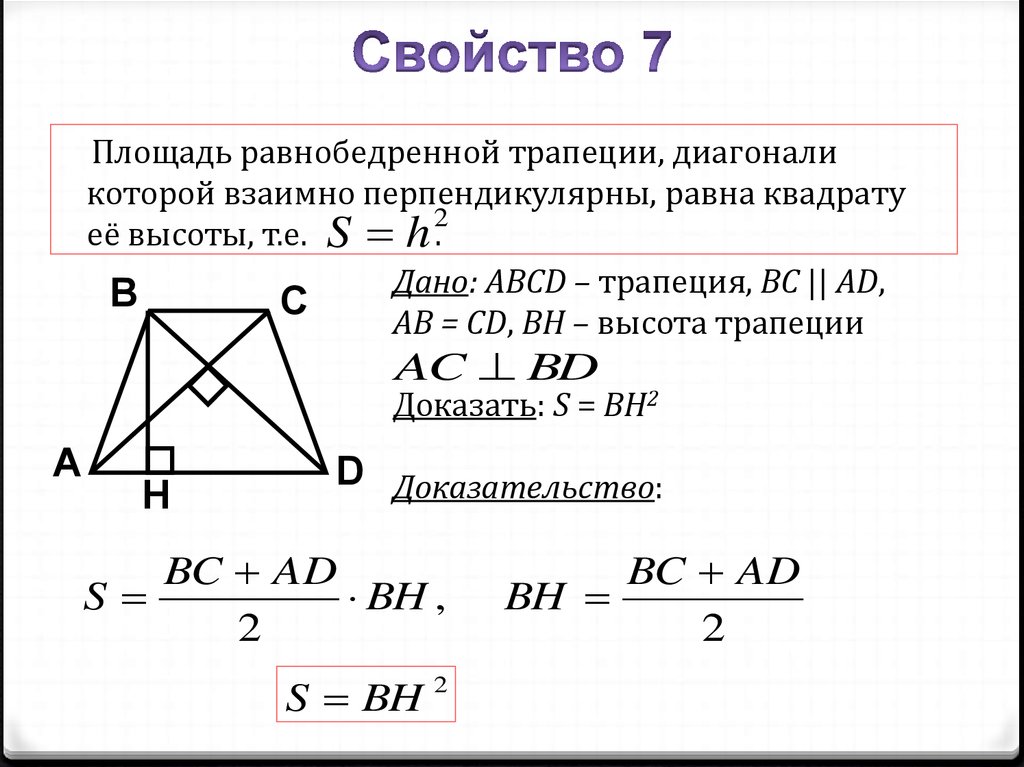
Площадь равнобедренной трапеции, диагоналикоторой взаимно перпендикулярны, равна квадрату
2
её высоты, т.е. S h .
Дано: ABCD – трапеция, BC || AD,
B
С
AB = CD, BH – высота трапеции
AC BD
Доказать: S = BH2
A
Н
D Доказательство:
BC AD
S
BH ,
2
S BH 2
BC AD
BH
2
16.
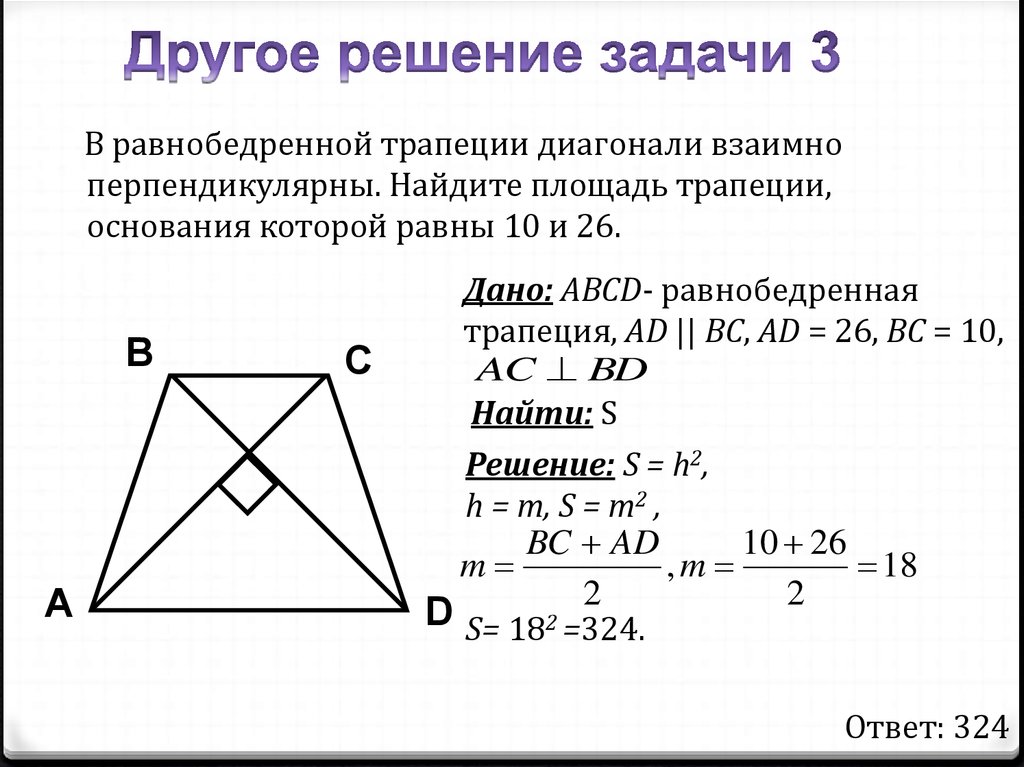
В равнобедренной трапеции диагонали взаимноперпендикулярны. Найдите площадь трапеции,
основания которой равны 10 и 26.
B
A
C
Дано: ABCD- равнобедренная
трапеция, AD || BC, AD = 26, BC = 10,
AC BD
Найти: S
Решение: S = h2,
h = m, S = m2 ,
BC AD
10 26
m
,m
18
2
2
D S= 182 =324.
Ответ: 324
17.
Найдите радиус окружности, если основания описаннойоколо неё равнобедренной трапеции равны 4 см и 16 см.
(ГИА)
B 4
С
Дано: окр.(О;r) вписана в
трапецию ABCD
10 8 O
AD || BC, AB = CD
AD = 16 cм, ВС = 4 см
D
A 6 H 16
4 L6
Найти: r
1
План
решения:
r
=
h
16
2
1) АВ = 10 ;
2) АН = 6 ;
3) ВН = 8 ;
4) r = 4
Ответ: 4
18.
Если в равнобедренную трапецию вписанаокружность, то её боковая сторона равна средней
линии трапеции.
B
A
С
Дано: окр.(О ; r) вписана
в трапецию ABCD, AD || BС
О
Доказать: AB AD BC
D
2
Доказательство:
по свойству четырёхугольника, описанного около
окружности:
AB + CD = AD + BC, AB = CD,
2AB = AD + BC,
AD BC
AB
2
19.
Высота равнобедренной трапеции, в которую можновписать окружность, является средним геометрическим
её оснований: h 2 a b.
B
Дано: окр.(О ; r) вписана
в трапецию ABCD
AD || BС
AB = CD, BC = a, AD = b,
h – высота трапеции
2
Доказать: h a b
С
a
O
A
b
D
20.
Кa
B
a
N2
h
b
2
A
C
H
b
M Р
Доказательство:
1)По свойству отрезков касательных,
проведённых из одной точки к
окружности:
a
b
AM = AN = , BN = BK =
2
2
2)Проведём высоту ВН и рассмотрим
ABH: H 90 , ВН = h
a b
b a ,
D
,
AH
AB
2
2
AB 2 AH 2 BH 2
2
2
a b b a a b b a a b b a
2
h
2
2
2
2
2a 2b 4ab
2
h
h 2 ab
2 2
4
По т. Пифагора:
21.
B4
Дано: окр.(О;r) вписана в
трапецию ABCD
AD || BC, AB = CD
AD = 16 cм, ВС = 4 см
Найти: r
1
Решение: r
h,
C
O
A
16
D
h =a∙b
2
h
2
16 4 4 2 8 (cм)
1
r 8 4 (cм)
2
Ответ: r = 4 см
22.
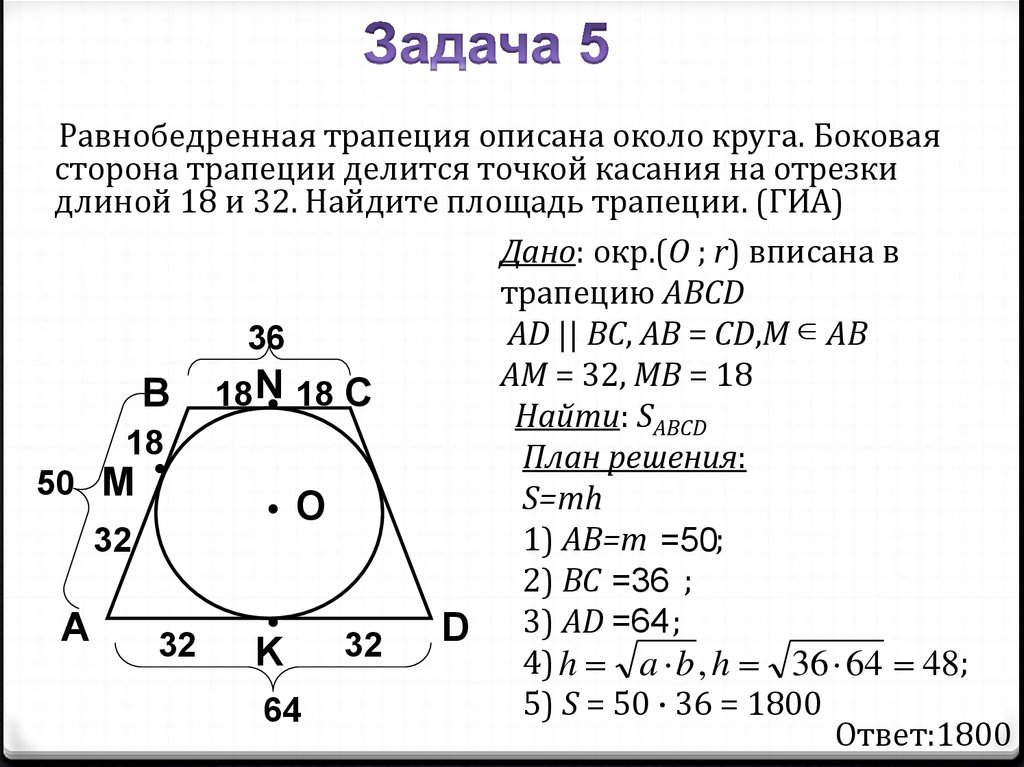
Равнобедренная трапеция описана около круга. Боковаясторона трапеции делится точкой касания на отрезки
длиной 18 и 32. Найдите площадь трапеции. (ГИА)
Дано: окр.(О ; r) вписана в
трапецию ABCD
AD || BC, AB = CD,М АВ
36
AM = 32, MB = 18
N
B 18 18 C
Найти: SABCD
18
План решения:
50 M
S=mh
О
1) АВ=m =50;
32
2) ВС =36 ;
3) AD =64 ;
A
D
32
32
K
4) h a b , h 36 64 48;
5) S = 50 · 36 = 1800
64
Ответ:1800
23.
Около круга радиуса r описана равнобедренная трапеция.Боковая сторона трапеции составляет с меньшим основанием
угол α. Найдите радиус круга, описанного около трапеции.
Дано: ABCD- трапеция, AD || BC,
описанная около окр.(О; r) и вписанная в
B
C
окр.(О1;R) AB = CD, B
Найти: R
BD
2r
2R
Решение:
по
теореме
синусов
О
sin A
D
BH
BH
2r
A Н
1). A 180 , sin A
, AB
,
AB
sin A sin
2r
2). AB HD , HD
;
sin
2
2r 1 sin 2
2r
2
2
2
2
3).BD BH HD , BD 2r
sin
sin
2
BD
r
1
sin
4).R
R
2 sin
sin 2
24.
В описанной около окружности равнобокой трапецииоснования относятся как 3 : 5. Из вершины меньшего
основания опущена высота на большее основание; точка
Н – основание высоты. Из точки Н опущен перпендикуляр
НЕ на боковую сторону трапеции. В каком отношении
точка Е делит боковую сторону? (ЕГЭ, С4)
B
Е
A
Н
Дано: окр.(О ; r) вписана в
C
трапецию ABCD
AD || BC, AB = CD, ВС : AD = 3 : 5
BH AD,
O
Е
a) HE AB;
б) НЕ СD
D Найти: a) AE : EB
б)DE : EC
25.
CB
O
Е
A
Н
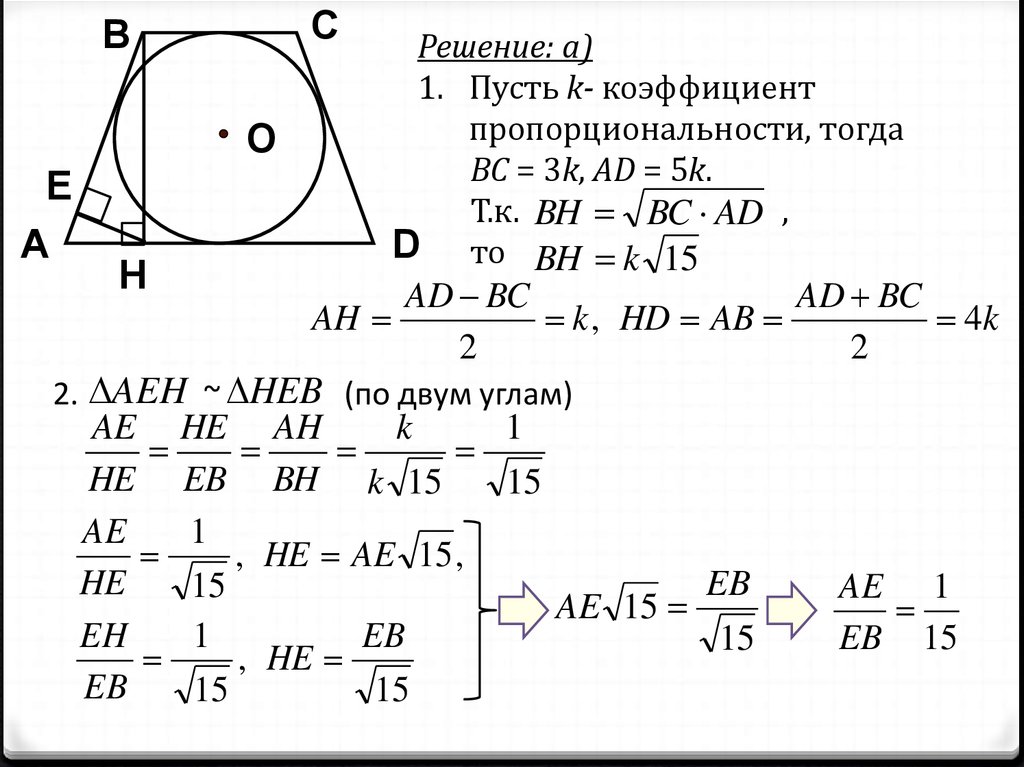
Решение: а)
1. Пусть k- коэффициент
пропорциональности, тогда
ВС = 3k, AD = 5k.
Т.к. BH BC AD ,
D то BH k 15
AD BC
AD BC
AH
k , HD AB
4k
2
2
2. AEH ~ HEB (по двум углам)
AE
HE
AE
HE
EH
EB
HE AH
k
1
EB BH k 15
15
1
, HE AE 15 ,
EB
15
AE 15
1
EB
15
, HE
15
15
AE 1
EB 15
26.
CB
O
A
Н
Решение: б)
3. ABE DHE (по гипотенузе и
острому углу)
Е
D
Ответ: а) 1 : 15; б) 1 : 3.
AB HD 4k
AH DE k
CE CD DE
CE 3k
DE 1
EC 3
27.
28.
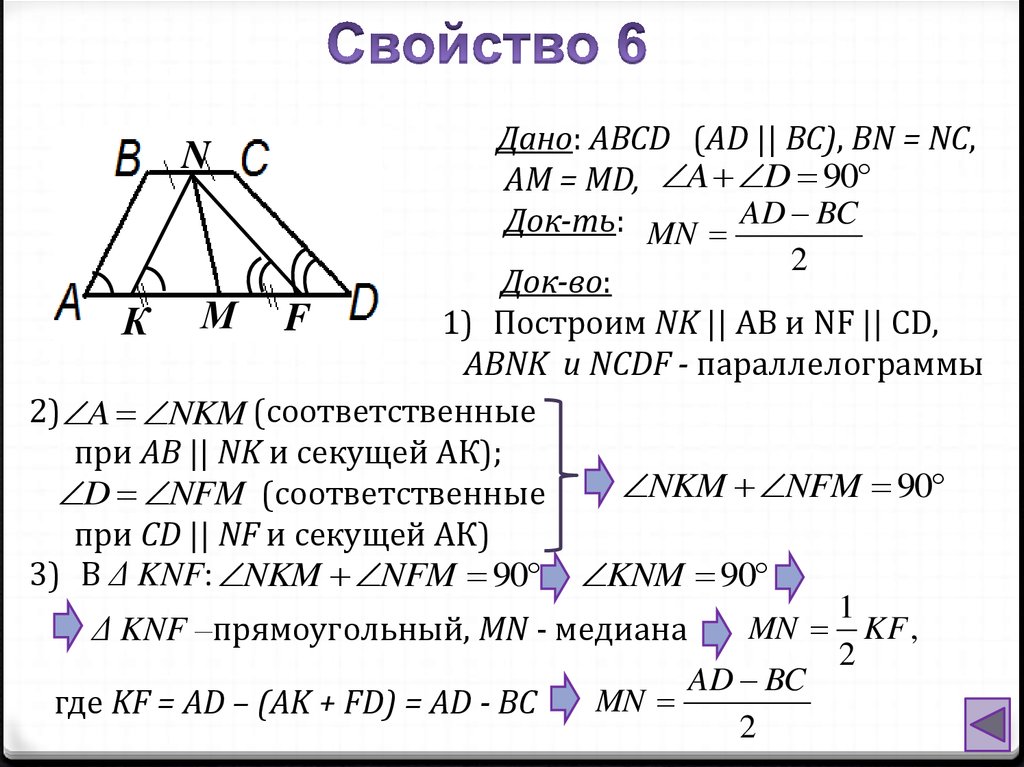
Дано: ABCD (AD || BC), BN = NC,AM = MD, A D 90
Док-ть: MN AD BC
2
Док-во:
1) Построим NK || AB и NF || CD,
К М F
ABNK и NCDF - параллелограммы
2) A NKM (соответственные
при AB || NK и секущей АК);
NKM NFM 90
D NFM (соответственные
при СD || NF и секущей АК)
3) В Δ KNF: NKM NFM 90 KNM 90
1
MN KF ,
Δ KNF –прямоугольный, MN - медиана
2
AD BC
MN
где KF = AD – (AK + FD) = AD - BC
2
N
29.
Если в трапецию ABCD вписана окружность c центром О,ab
r
, где OA =а и OD= b .
то
2
2
a b
Док-во:
1) AO OD ;
Дано: окр.(О ; r) вписана в
трапецию ABCD
AD || BC, ОА = a,
OD = b
ab
Док-ть: r
,
1
1
2
2
2) S AOD ab, S r a b
2
2
1
1
ab r a 2 b 2
r
2
2
a 2 b2
ab
a2 b2
30.
OR
Радиус окружности,
описанной около
трапеции, равен радиусу
окружности, описанной
около треугольника,
вершины которого
лежат в вершинах
данной трапеции.

















 mathematics
mathematics








