Similar presentations:
Решении планиметрических задач (метод площадей)
1. РЕШЕНИИ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ (метод площадей)
2.
Наши знания никогда немогут иметь конца именно
потому, что предмет
познания бесконечен.
Блез Паскаль.
3.
Свойства площадей:1.Площадь фигуры является
неотрицательным числом.
2.Площади равных фигур равны.
3.Если фигура разделена на части,
то площадь всей фигуры равна
сумме площадей образовавшихся
частей.
4.
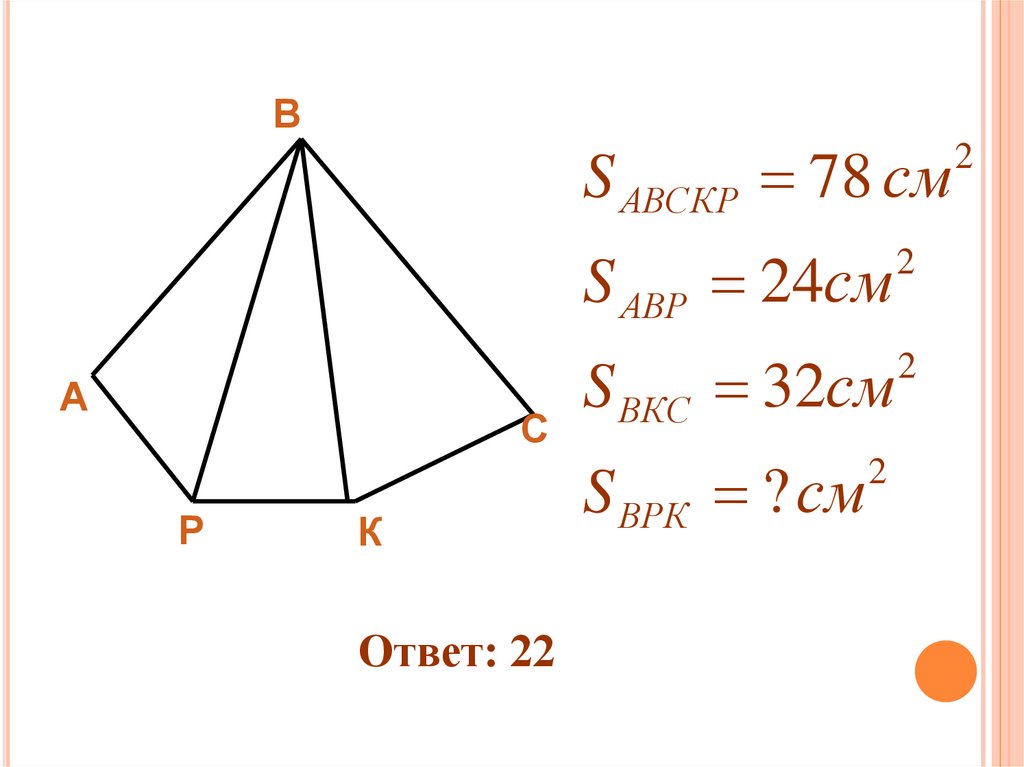
ВS АВСКР 78 см
А
С
Р
К
Ответ: 22
S АВР 24см
2
S ВКС 32см
2
S ВРК ? см
2
2
5.
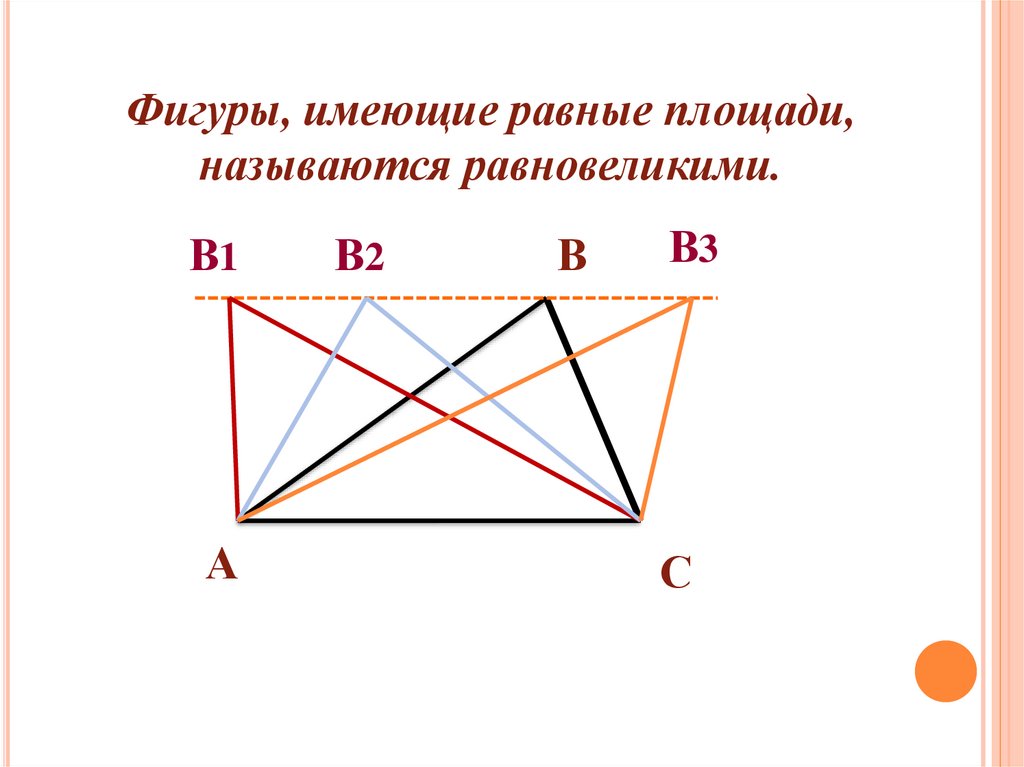
Фигуры, имеющие равные площади,называются равновеликими.
В1
А
В2
В
В3
С
6.
Равные фигуры всегда равновелики, норавновеликие фигуры могут быть
неравными.
7.
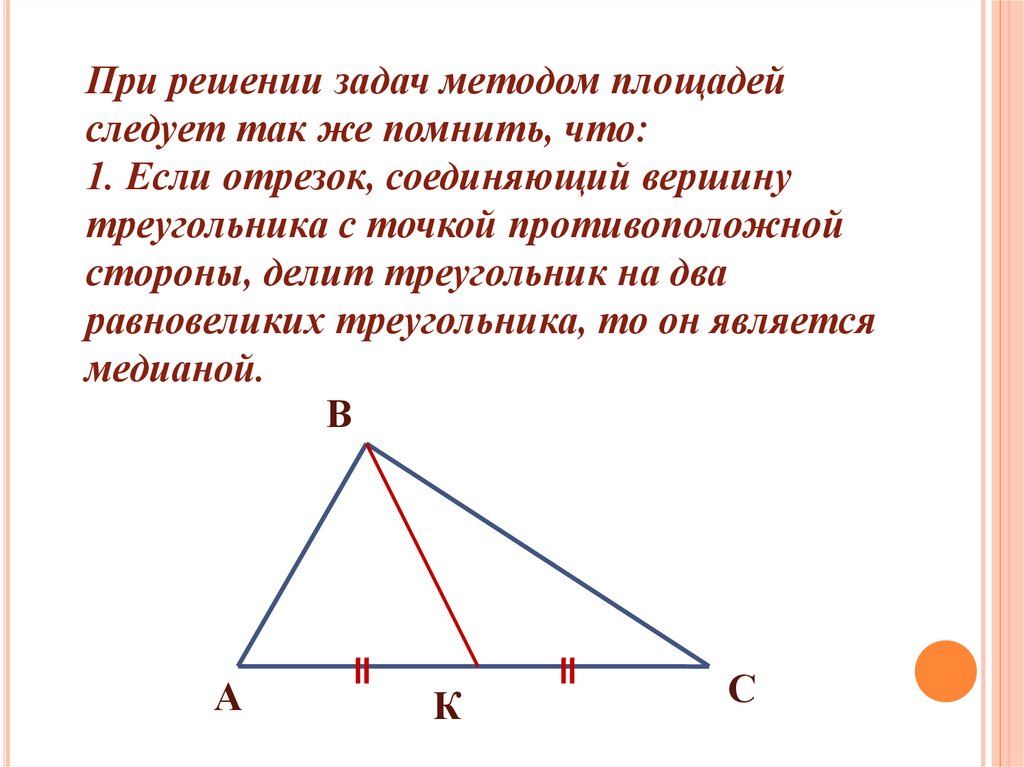
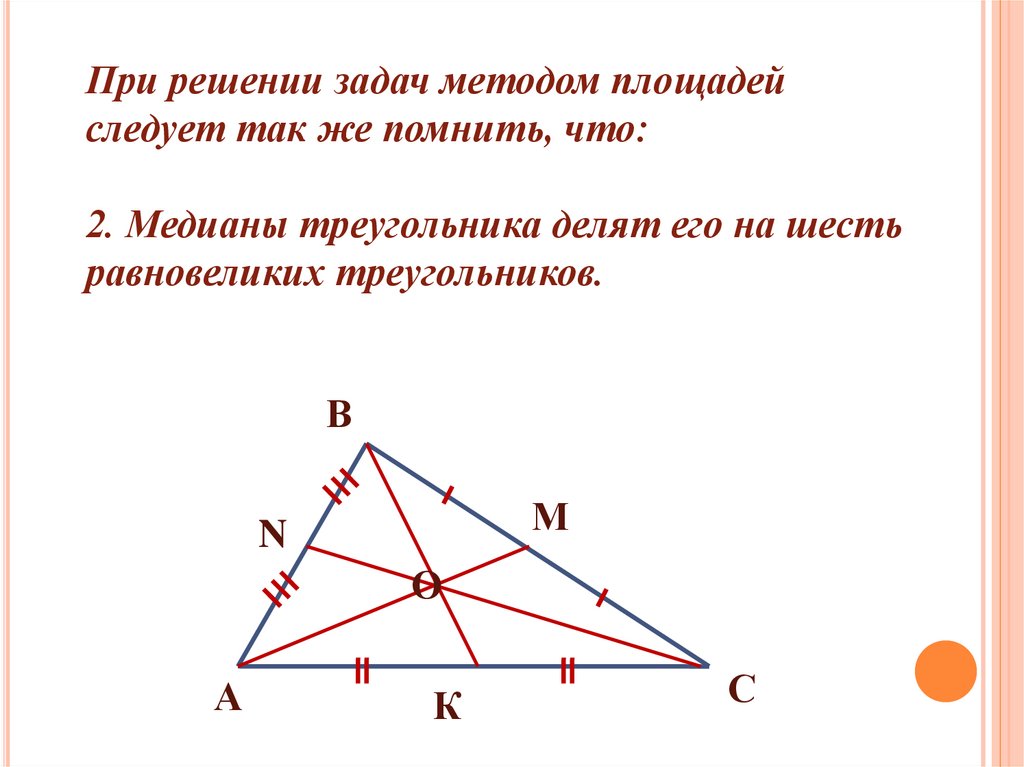
При решении задач методом площадейследует так же помнить, что:
1. Если отрезок, соединяющий вершину
треугольника с точкой противоположной
стороны, делит треугольник на два
равновеликих треугольника, то он является
медианой.
В
А
К
С
8.
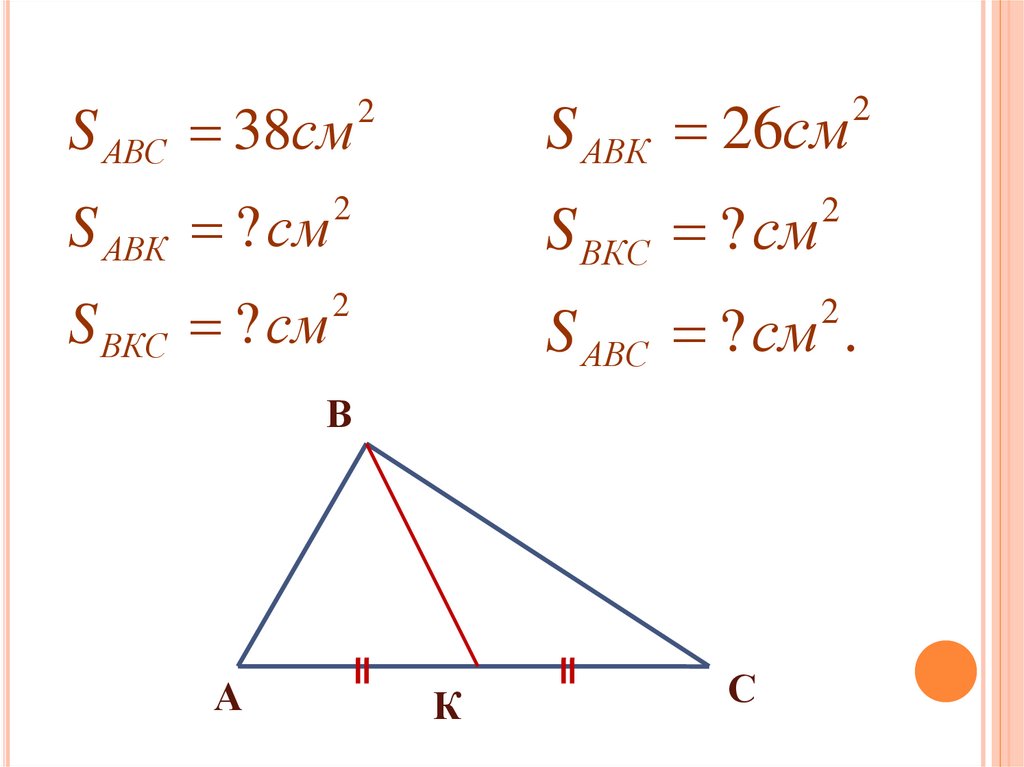
S АВС 38смS АВК 26см
2
2
S АВК ? см
2
S ВКС ? см
S ВКС ? см
2
S АВС ? см .
2
В
А
2
К
С
9.
При решении задач методом площадейследует так же помнить, что:
2. Медианы треугольника делят его на шесть
равновеликих треугольников.
В
М
N
O
А
К
С
10.
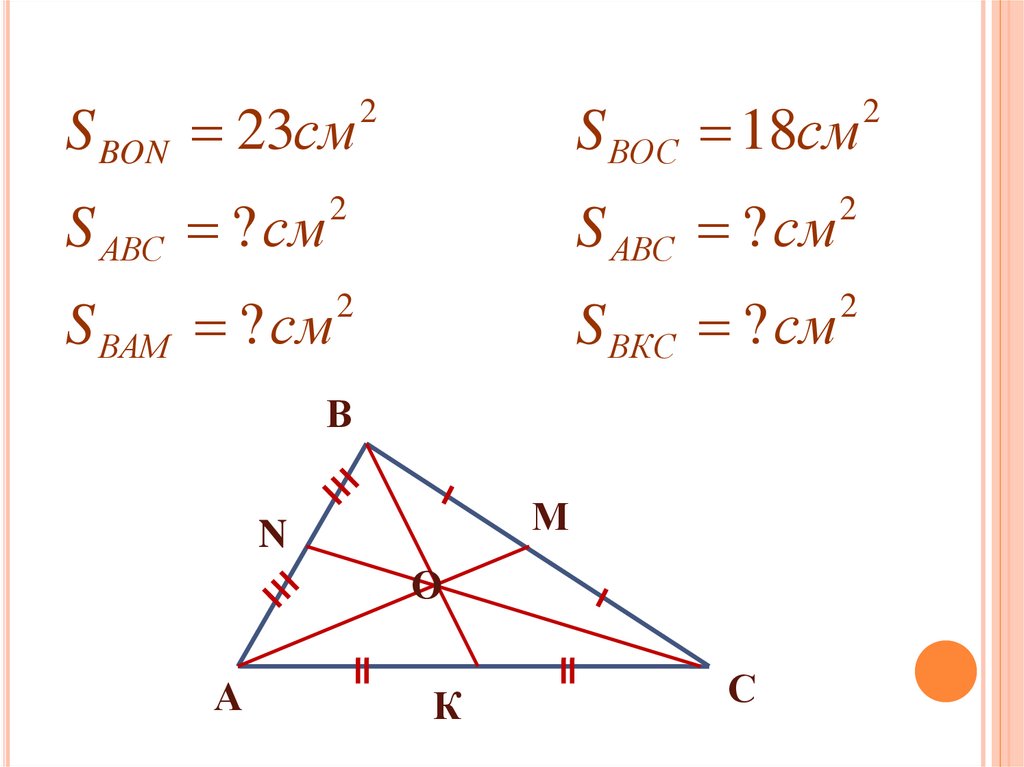
S BON 23смS АВC ? см
S ВОС 18см
2
2
S АВС ? см
2
S ВAM ? см
S ВКС ? см
2
2
В
М
N
O
А
К
С
2
11.
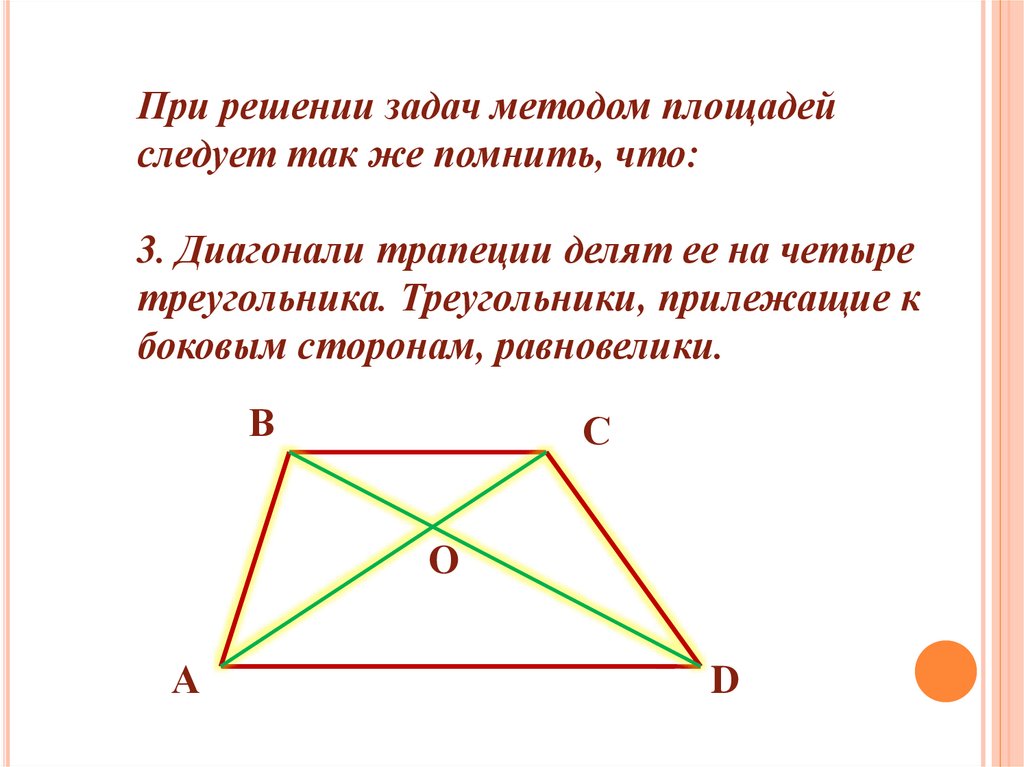
При решении задач методом площадейследует так же помнить, что:
3. Диагонали трапеции делят ее на четыре
треугольника. Треугольники, прилежащие к
боковым сторонам, равновелики.
В
С
O
А
D
12.
ВС
O
А
D
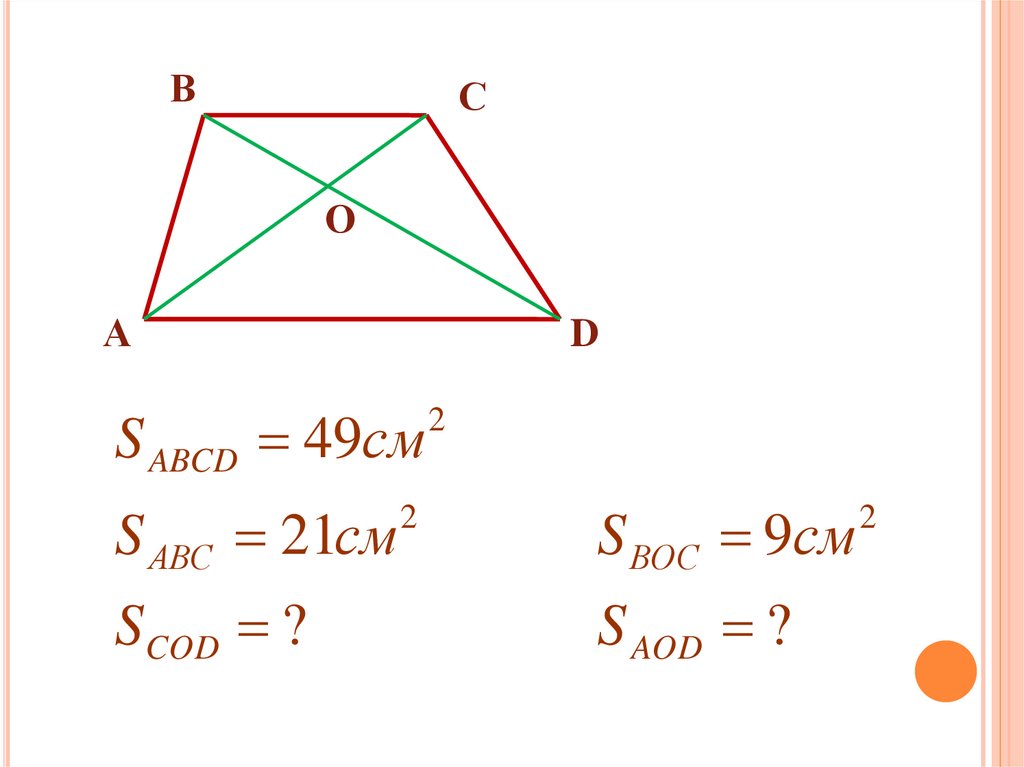
S ABCD 49см
S АВC 21см
SCOD ?
2
2
S ВOC 9см
S AOD ?
2
13.
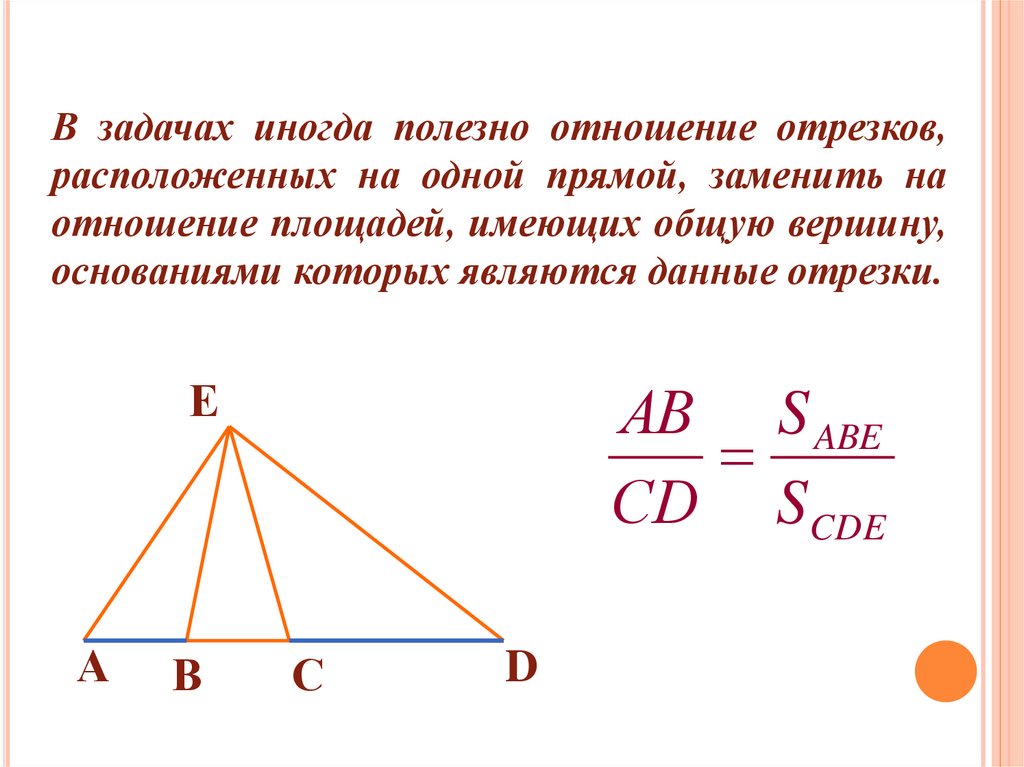
В задачах иногда полезно отношение отрезков,расположенных на одной прямой, заменить на
отношение площадей, имеющих общую вершину,
основаниями которых являются данные отрезки.
Е
А
В
АВ S ABE
СD SCDE
С
D
14.
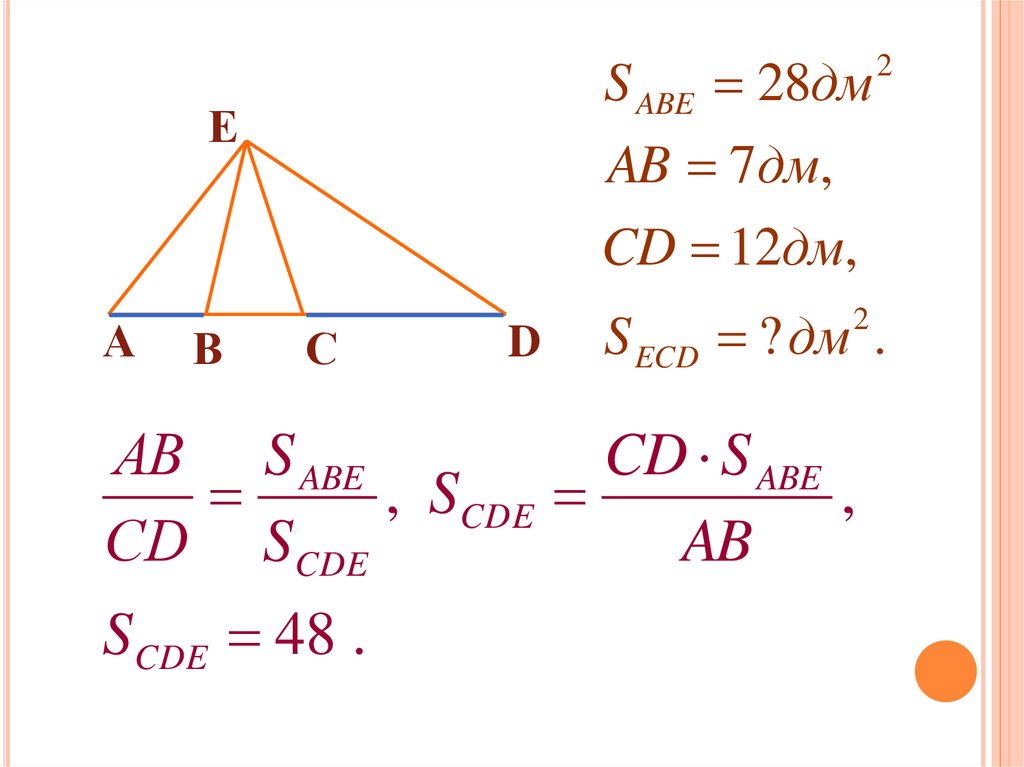
S ABE 28дмЕ
А
В
2
AB 7дм,
CD 12дм,
С
D
S ECD ? дм .
2
АВ S ABE
CD S ABE
, SCDE
,
СD SCDE
AB
SCDE 48 .
15.
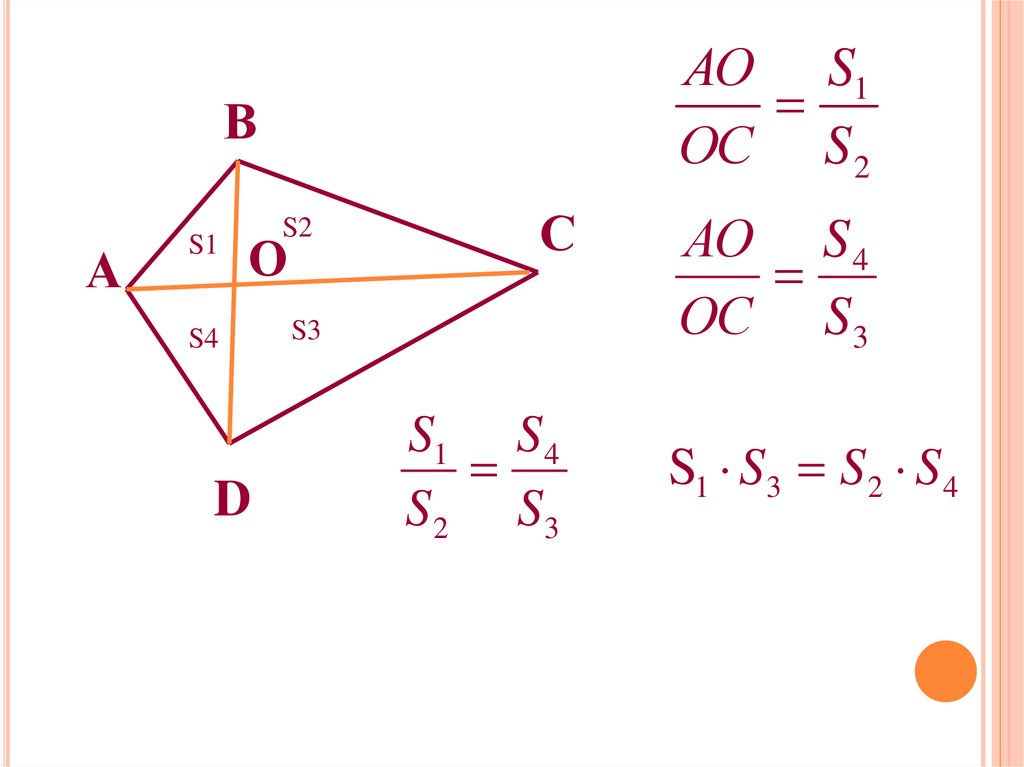
АО S1ОС S 2
В
А
S1
S2
О
S4
D
С
S3
S1 S 4
S 2 S3
АО S 4
ОС S3
S1 S3 S 2 S 4
16.
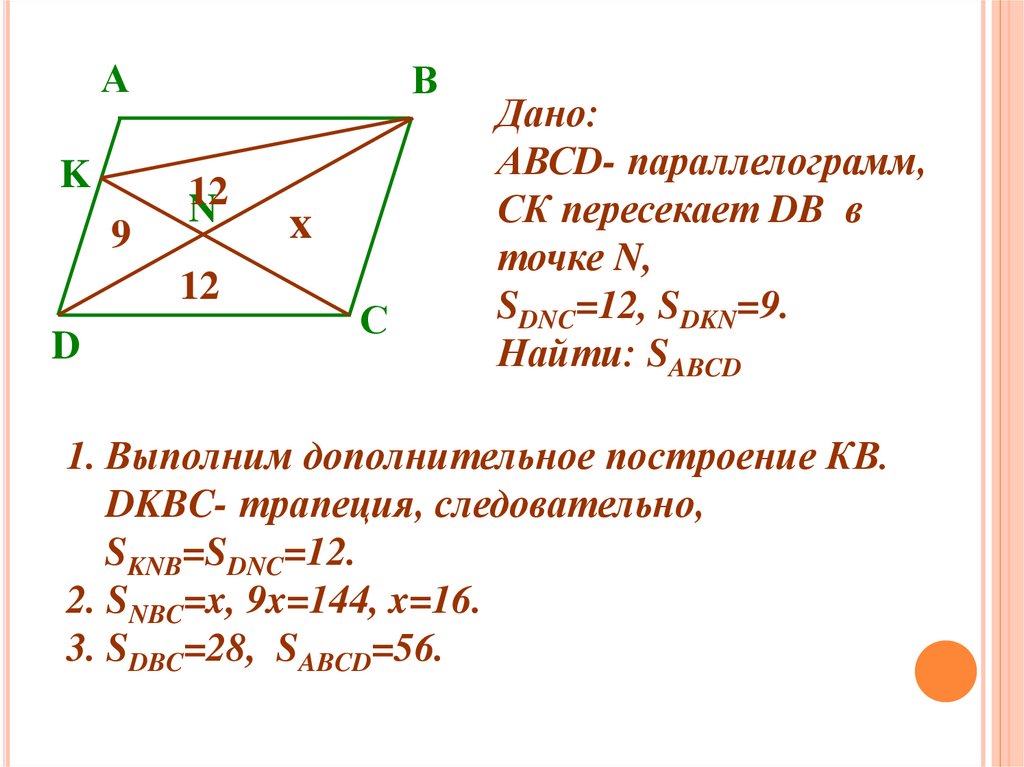
Задача.Вершина
С параллелограмма АВСD
соединена с точкой K на стороне AD.
Отрезок СК пересекает диагональ BD в
точке N. Площадь треугольника CDN равна
12, а площадь треугольника DKN равна 9.
Найдите площадь параллелограмма ABCD.
17.
АK
9
В
12
N
12
D
x
С
Дано:
АВСD- параллелограмм,
СК пересекает DB в
точке N,
SDNC=12, SDKN=9.
Найти: SABCD
1. Выполним дополнительное построение КВ.
DKBC- трапеция, следовательно,
SKNB=SDNC=12.
2. SNBC=x, 9x=144, x=16.
3. SDBC=28, SABCD=56.
18.
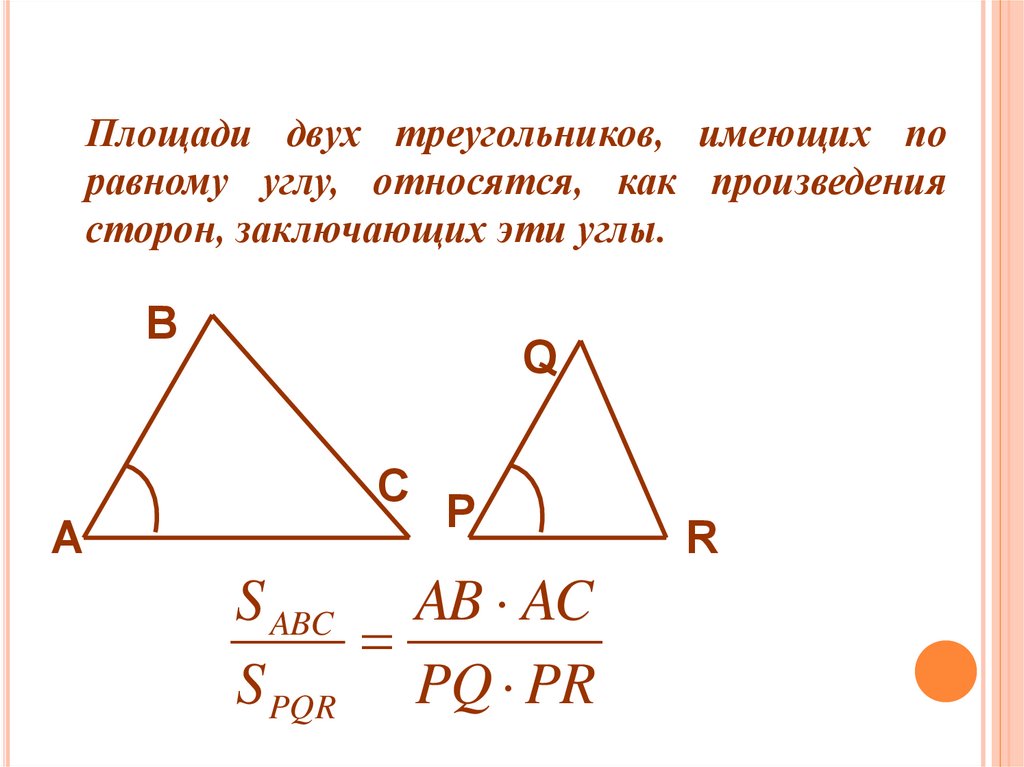
Площади двух треугольников, имеющих поравному углу, относятся, как произведения
сторон, заключающих эти углы.
В
Q
С
А
Р
S ABC AB AC
S PQR PQ PR
R
19.
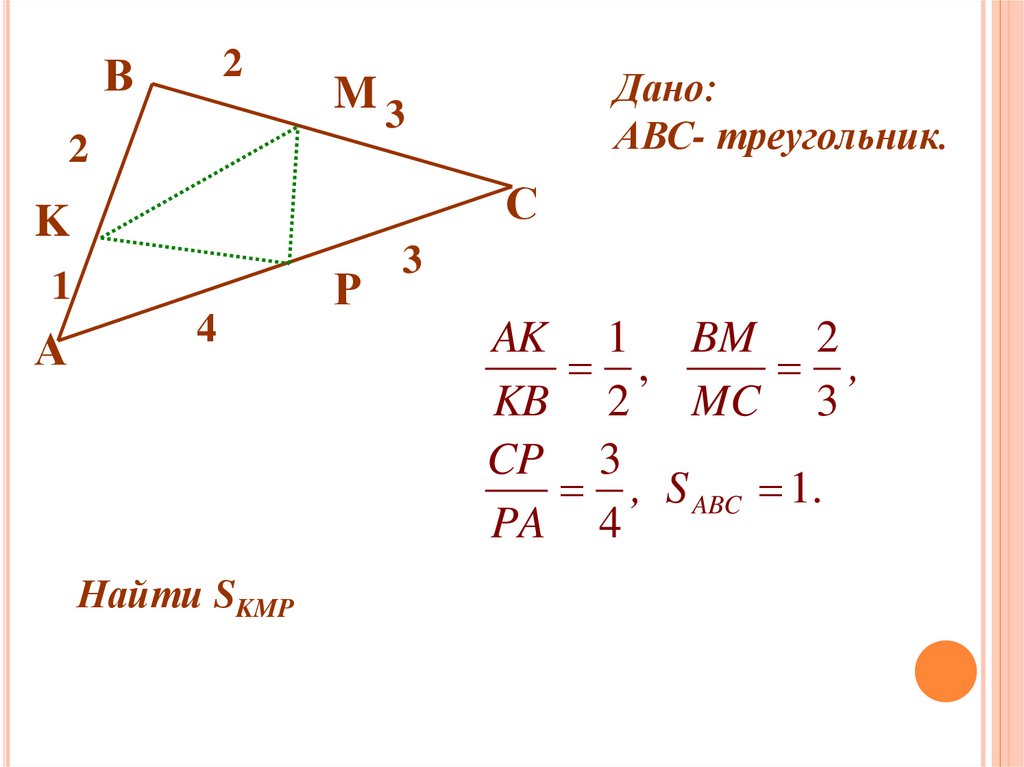
Задача.На сторонах AB, BC и СА треугольника
АВС взяты точки К, M и Р так, что
АК:КВ=1:2, ВМ:МС=2:3, СР:РА=3:4.
Площадь треугольника АВС равна 1.
Найдите площадь треугольника КMР.
20.
2В
2
С
K
Р
1
А
Дано:
АВС- треугольник.
M3
4
Найти SKMP
3
AK 1 BM 2
,
,
KB 2 MC 3
CP 3
, S ABC 1.
PA 4
21.
S AKP AK AP 1 4 41.
,
S ABC AB AC 7 3 21
S KBM KB BM 2 2 4
2.
,
S ABC
BA BC 3 5 15
S PCM PC CM 3 3 9
3.
.
S ABC
CB CA 5 7 35
22.
4.S ABC 1,4
4
9
S AKP , S KBM , S PMC .
21
15
35
4 4 9 2
5.1 .
21 15 35 7
2
Ответ:
7
23.
«Геометрия является самыммогущественным средством для
изощрения наших умственных
способностей и дает нам возможность
правильно мыслить и рассуждать».
Галилео Галилей









 mathematics
mathematics








