Similar presentations:
Четырехугольники. Методика обучения решению планиметрических задач. Лекция 1
1.
МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ ПЛАНИМЕТРИЧЕСКИХЗАДАЧ
Лекция 1
ЧЕТЫРХУГОЛЬНИКИ
Ларионова Наталья Евгеньевна,
МАОУ Лицей математики и информатики
2.
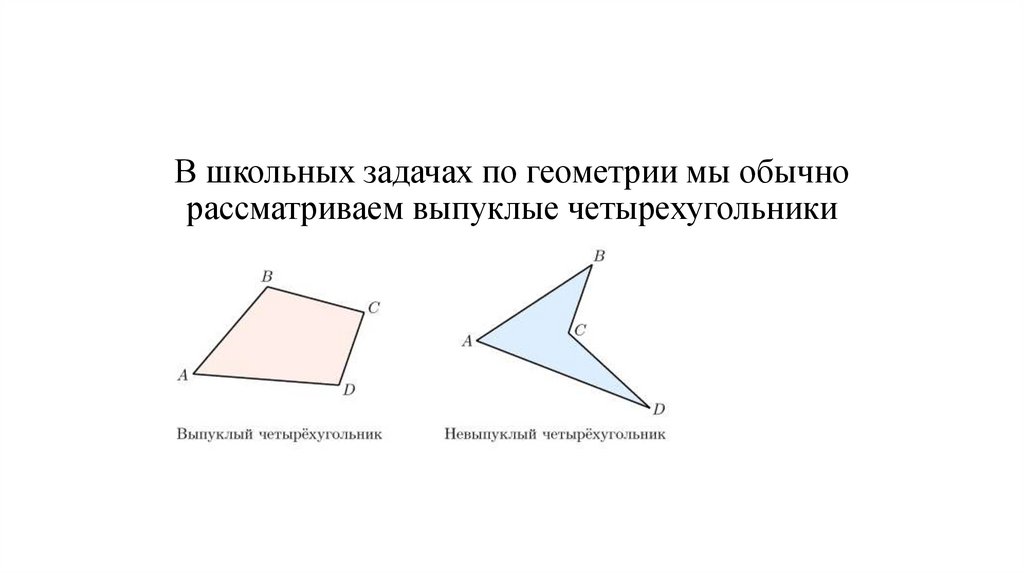
В школьных задачах по геометрии мы обычнорассматриваем выпуклые четырехугольники
3.
• В чем разница между ними? Если любые две точки выпуклого многоугольника соединитьотрезком — весь отрезок будет лежать внутри многоугольника. Для невыпуклых фигур это
не выполняется.
• Сумма углов выпуклого четырехугольника равна 360 градусов.
• Произвольные четырехугольники в задачах по геометрии встречаются редко.
Намного чаще — такие, у которых есть параллельные стороны. Это параллелограмм, ромб,
квадрат, прямоугольник и трапеция.
4.
В таблице собраны ихопределения и свойства.
5.
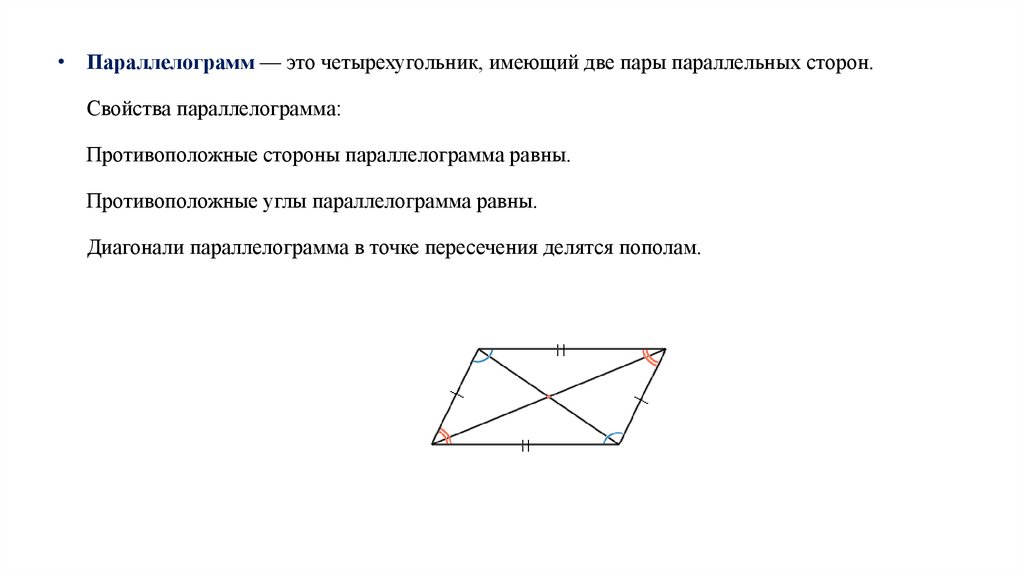
• Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон.Свойства параллелограмма:
Противоположные стороны параллелограмма равны.
Противоположные углы параллелограмма равны.
Диагонали параллелограмма в точке пересечения делятся пополам.
6.
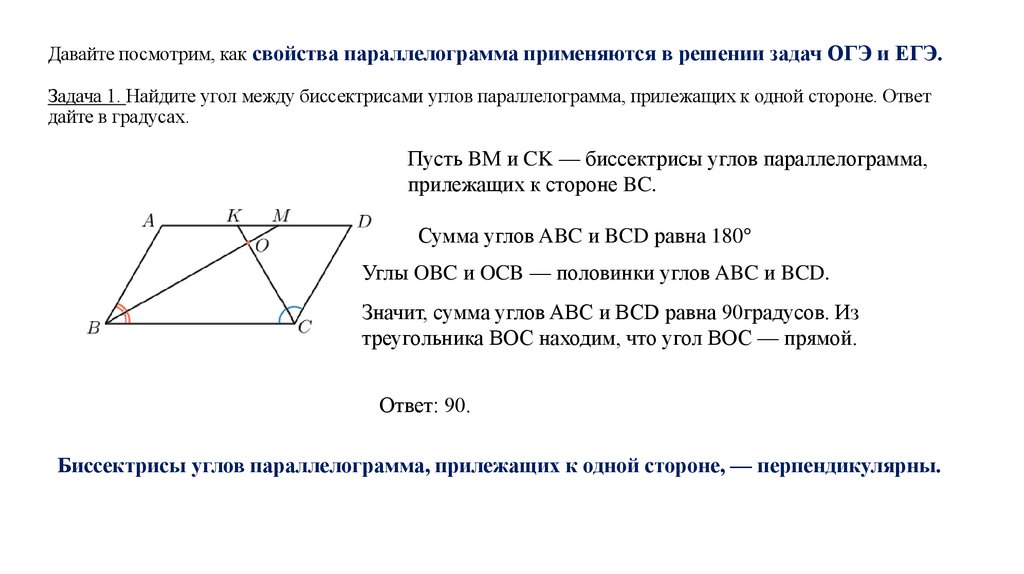
Давайте посмотрим, как свойства параллелограмма применяются в решении задач ОГЭ и ЕГЭ.Задача 1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ
дайте в градусах.
Пусть BМ и CK — биссектрисы углов параллелограмма,
прилежащих к стороне BC.
Сумма углов ABC и BCD равна 180°
Углы OBC и OCB — половинки углов ABC и BCD.
Значит, сумма углов ABC и BCD равна 90градусов. Из
треугольника BOC находим, что угол BOC — прямой.
Ответ: 90.
Биссектрисы углов параллелограмма, прилежащих к одной стороне, — перпендикулярны.
7.
Задача 2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежитпротивоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Легко доказывается и другое свойство биссектрис параллелограмма:
Биссектрисы противоположных углов параллелограмма — параллельны.
8.
Задача 2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к однойстороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5.
Найдите его большую сторону.
Найдем на этом рисунке накрест лежащие углы.
Углы DAE и BEA, а также CED и ADE — накрест лежащие.
Накрест лежащие углы равны. Значит, угол DAE равен углу BEA,
а угол CED — углу ADE.
Получаем, что треугольники ABE и CDE — равнобедренные, то
есть BE=AB, а EC=CD.
Тогда BC = 5+5=10.
• Биссектриса угла параллелограмма отсекает от него
равнобедренный треугольник.
9.
Прямоугольник и его свойстваПрямоугольник — это параллелограмм, у которого все углы прямые.
Диагонали прямоугольника равны.
10.
Задача1. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 6.Найдите диагональ данного прямоугольника.
Рассмотрим прямоугольный треугольник ABD. Найдем,
чему равен угол DBA и его синус, а затем найдем DB.
Ответ: 12.
11.
Рассмотрим еще одну задачу, в которой применяются свойства диагоналей прямоугольника.Задача 2. Острые углы прямоугольного треугольника равны 24°и 66°. Найдите угол между
высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Казалось бы, при чем здесь прямоугольник? Дан прямоугольный
треугольник, из вершины прямого угла проведены высота и
медиана. А что можно сказать о длине этой медианы?
Давайте достроим чертеж до прямоугольника. Поскольку диагонали
прямоугольника равны (это свойство прямоугольника) и делятся
пополам в точке пересечения, отрезки CM, BM и AM тоже будут
равны. Каждый из них равен половине диагонали прямоугольника.
Мы доказали теорему:
В прямоугольном треугольнике медиана, проведенная к гипотенузе,
равна половине гипотенузы.
12.
• Итак, BM = CM, значит, треугольник BMC равнобедренный, и уголBCM равен 24°.
• По свойству высоты, проведенной из вершины прямого угла,
• Углы ACH и ABC равны 24°.
• Тогда угол MCH (между медианой и высотой треугольника ABC) равен
90°-24°-24°=42°.
• Ответ: 42.
13.
Центр описанной окружности — точка, равноудаленная от всех вершин треугольника. Очевидно,эта точка — середина гипотенузы.
В прямоугольном треугольнике центром описанной окружности является середина гипотенузы.
• Задача 1. Найдите диагональ прямоугольника, вписанного в окружность, радиус которой
равен 5.
Проведем диагональ AC.
Получим, что AC равна 2R.
Ответ: 10.
14.
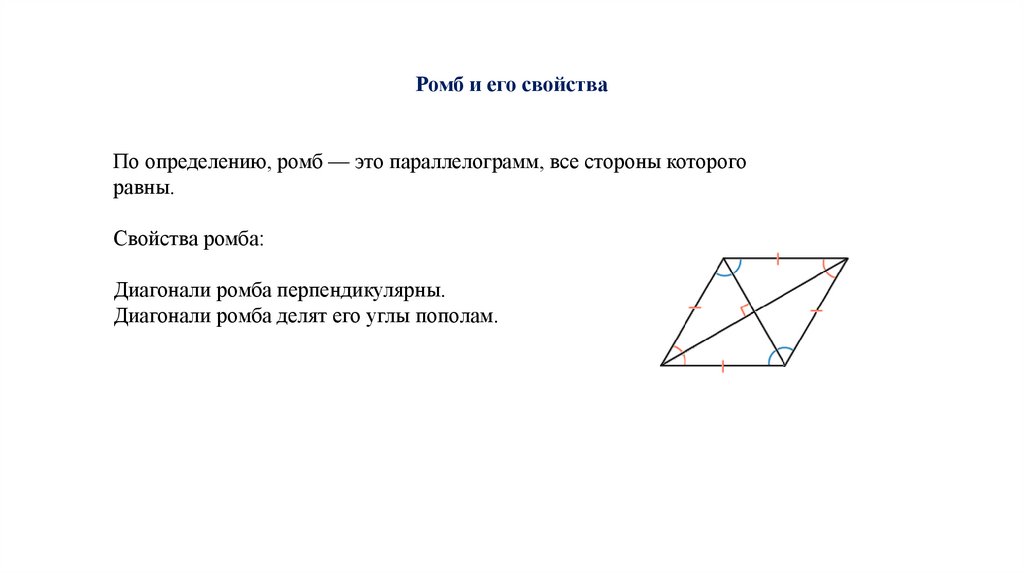
Ромб и его свойстваПо определению, ромб — это параллелограмм, все стороны которого
равны.
Свойства ромба:
Диагонали ромба перпендикулярны.
Диагонали ромба делят его углы пополам.
15.
Воспользуемся свойствами ромба для решения задач.Задача 1. Найдите меньшую диагональ ромба, стороны которого равны 2, а острый угол равен 60°
Проведем меньшую диагональ ромба и рассмотрим треугольник ADB.
Поскольку AD = DB, а угол DAB равен 60°, треугольник ADB —
равносторонний.
Следовательно, меньшая диагональ ромба равна 2.
16.
1. Найдите высоту ромба, сторона которого равна 3, а острый угол равен 60?Один из подходов к решению задач по геометрии — метод
площадей.
Он состоит в том, что площадь фигуры выражается двумя
разными способами, а затем из полученного уравнения
находится неизвестная величина.
Пусть a — сторона ромба.
Отсюда найдем высоту
17.
2. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.Пусть диагонали ромба равны 6x и 8x.
Диагонали ромба перпендикулярны, значит, треугольник AOB — прямоугольный.
По теореме Пифагора AB^2 = AO^2 + OB^2,
AB^2 = 9x^2 + 16x^2,
AB^2 = 25x^2,
Отсюда AB=5x.
Поскольку периметр равен 200,
5x ∙ 4=200,
x=10,
AB=50, а диагонали ромба равны 60 и 80.
Нам надо найти высоту ромба.
Давайте запишем, чему равна площадь ромба. С одной стороны, S = a∙ h. С другой стороны, площадь
ромба складывается из площадей двух равных треугольников ABC и ADC, то есть равна 60 ∙ 40 = 2400.
Отсюда h = S : a = 2400 : 50 = 48.
Ответ: 48.
18.
Квадрат — это прямоугольник, у которого все стороны равны.Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
• Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и
ромба.
• Квадрат относится к правильным многоугольникам. У правильного многоугольника все
стороны равны и все углы равны.
• Перечислим свойства квадрата:
• Все углы квадрата — прямые, все стороны квадрата — равны.
19.
2. Диагонали квадрата равны и пересекаются под прямым углом.3. Диагонали квадрата делятся точкой пересечения пополам.
4. Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
5. Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника.
Периметр квадрата P в 4 раза больше его стороны и равен: P=4a.
Площадь квадрата равна квадрату его стороны: S=a^2.
20.
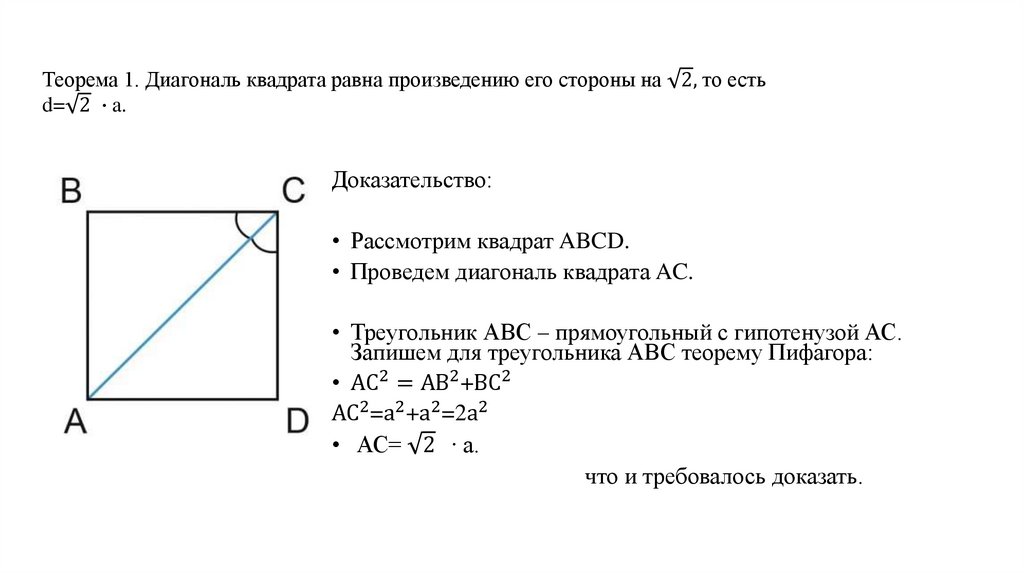
Теорема 1. Диагональ квадрата равна произведению его стороны на 2, то естьd= 2 ∙ a.
Доказательство:
• Рассмотрим квадрат ABCD.
• Проведем диагональ квадрата AC.
• Треугольник АВС – прямоугольный с гипотенузой АС.
Запишем для треугольника АВС теорему Пифагора:
• АС2 = АВ2 +ВС2
АС2 =а2 +а2 =2а2
• АС= 2 ∙ a.
что и требовалось доказать.
21.
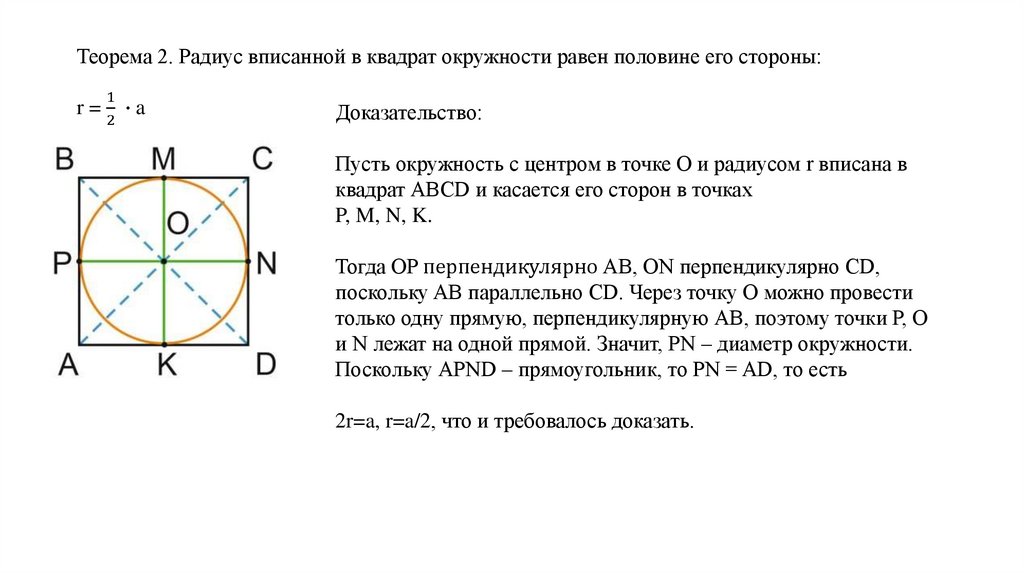
Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:r=
1
∙a
2
Доказательство:
Пусть окружность с центром в точке О и радиусом r вписана в
квадрат АВСD и касается его сторон в точках
P, M, N, K.
Тогда OP перпендикулярно AB, ON перпендикулярно CD,
поскольку AB параллельно CD. Через точку О можно провести
только одну прямую, перпендикулярную АВ, поэтому точки Р, О
и N лежат на одной прямой. Значит, PN – диаметр окружности.
Поскольку АРND – прямоугольник, то PN = AD, то есть
2r=a, r=a/2, что и требовалось доказать.
22.
Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:R=
2
∙ a.
2
• Доказательство:
Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения
пополам.
Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой
R = d/2 (d=AC=BD).
Это и есть описанная около квадрата АВСD окружность.
По теореме 1:
Тогда
что и требовалось доказать.
23.
Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описаннойокружностей:
P=4a=4 2 R=8r.
!Четырехугольник является квадратом, если выполняется хотя бы одно из условий:
Все стороны равны и среди внутренних углов есть прямой угол.
Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

















 mathematics
mathematics








