Similar presentations:
Свойства четырехугольников. Решение задач
1. МОУ «СОШ с. Брыковка Духовницкого района Саратовской области» Шабанова Татьяна Александровна учитель математики 2013
2. Цели урока:
• Повторить, обобщить исистематизировать знания
обучающихся по данной теме.
• Сформировать навык применения
изученных свойств при решении
задач.
3.
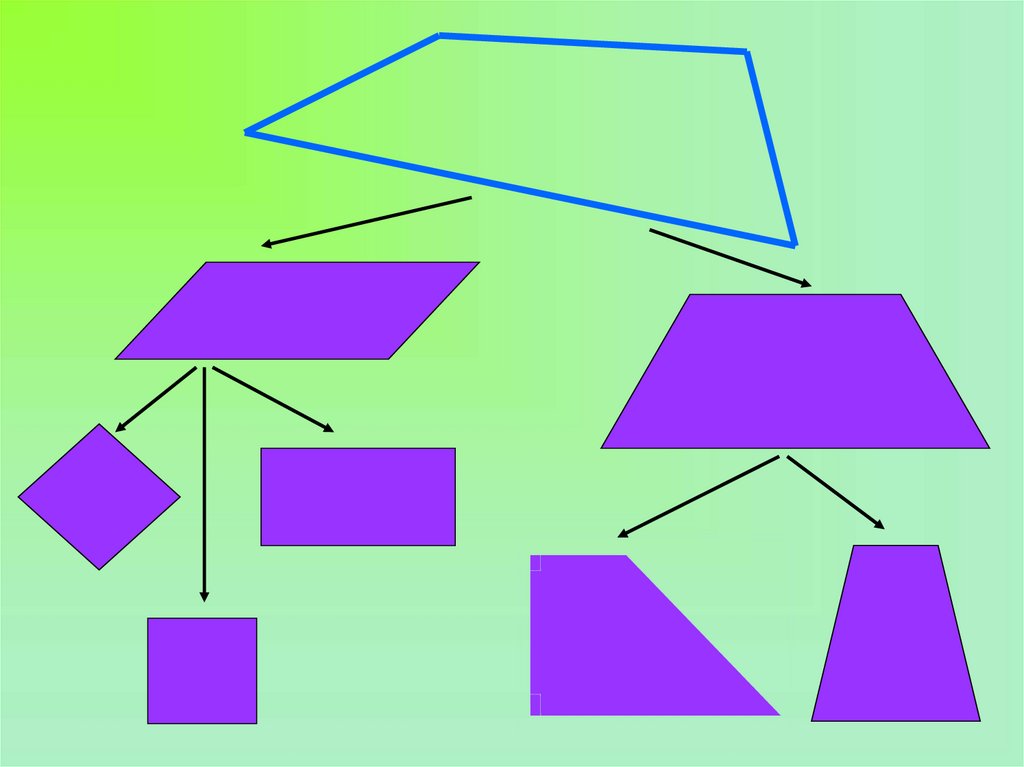
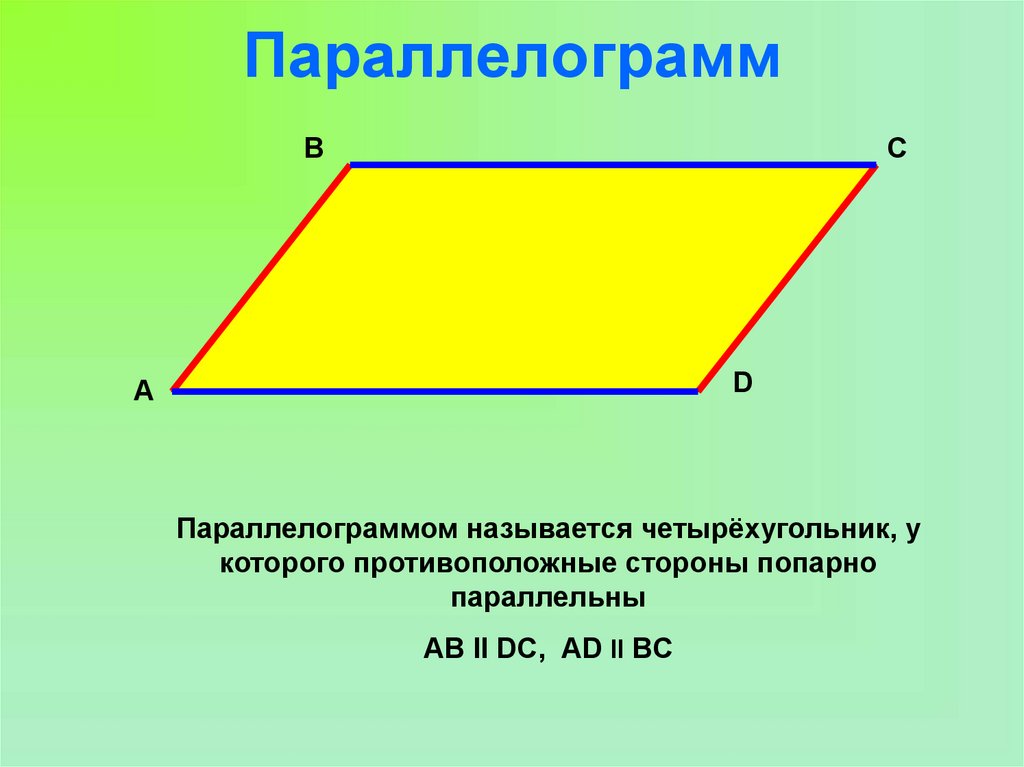
4. Параллелограмм
ВС
D
А
Параллелограммом называется четырёхугольник, у
которого противоположные стороны попарно
параллельны
АВ ІІ DC, АD ІІ BC
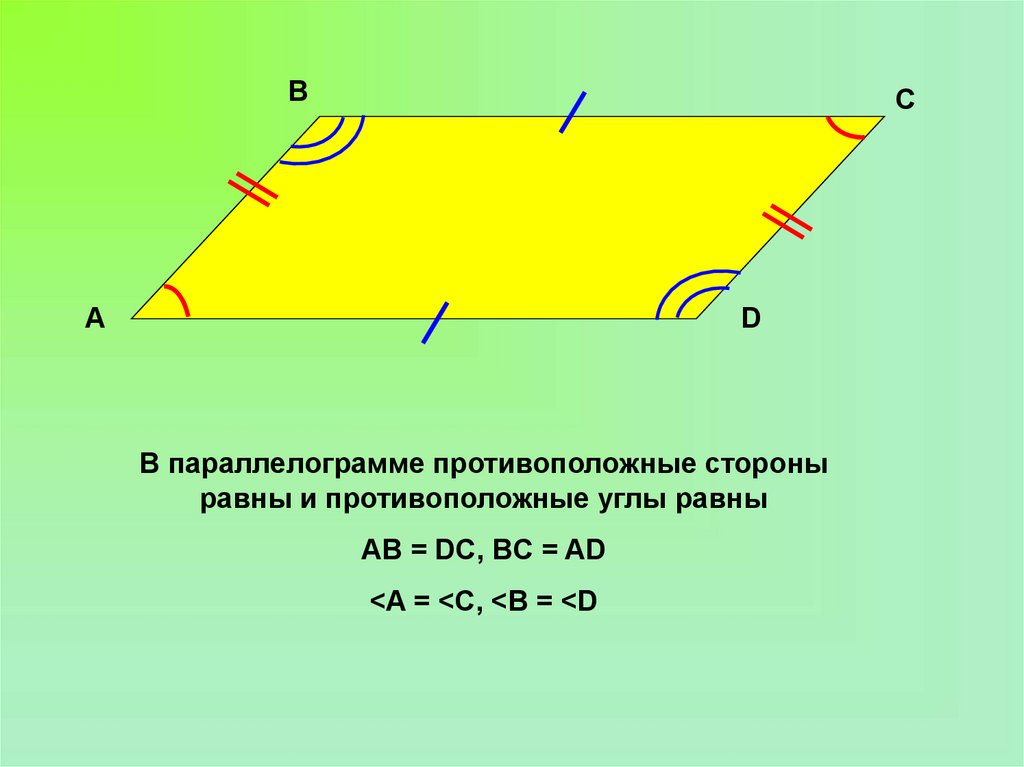
5.
BC
A
D
В параллелограмме противоположные стороны
равны и противоположные углы равны
AB = DC, BC = AD
<A = <C, <B = <D
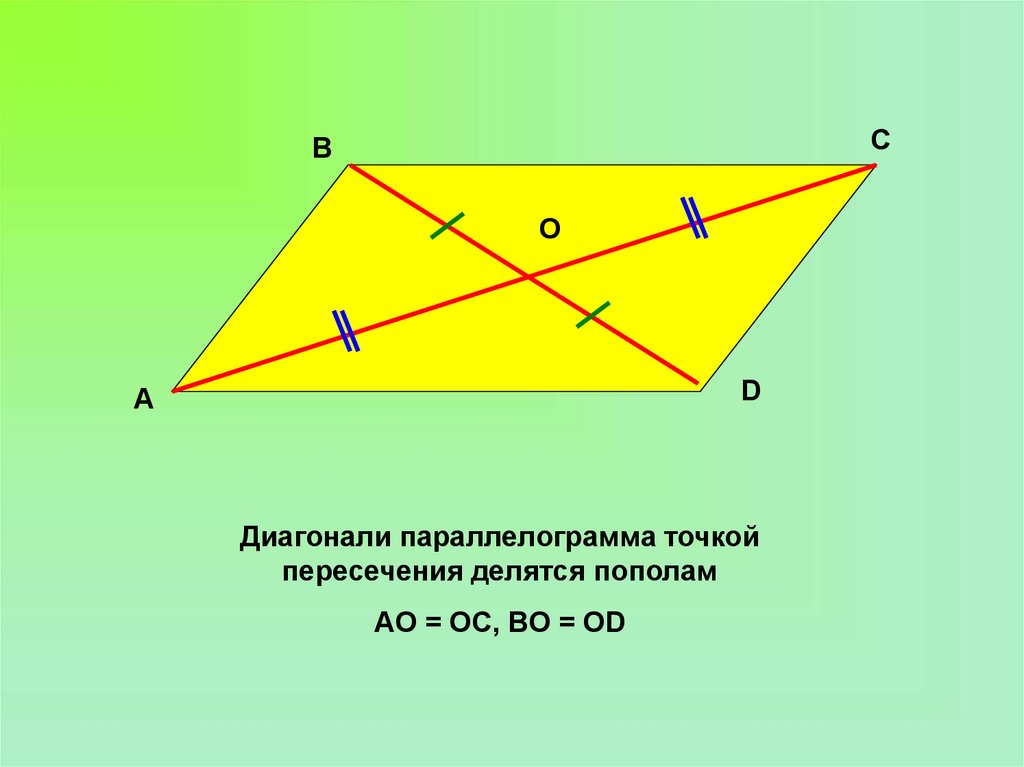
6.
CB
O
D
A
Диагонали параллелограмма точкой
пересечения делятся пополам
AO = OC, BO = OD
7.
ВС
D
А
Сумма углов, прилежащих к одной
стороне, равна 180°
<А + <В = 180 °
8.
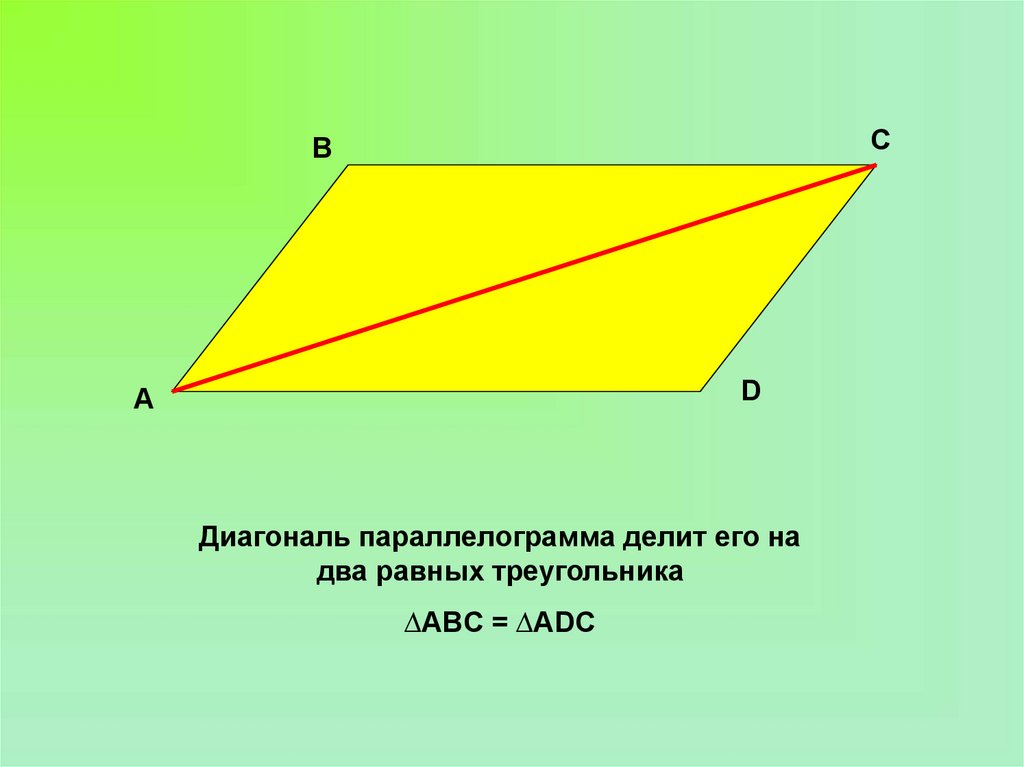
CB
D
A
Диагональ параллелограмма делит его на
два равных треугольника
∆ABC = ∆ADC
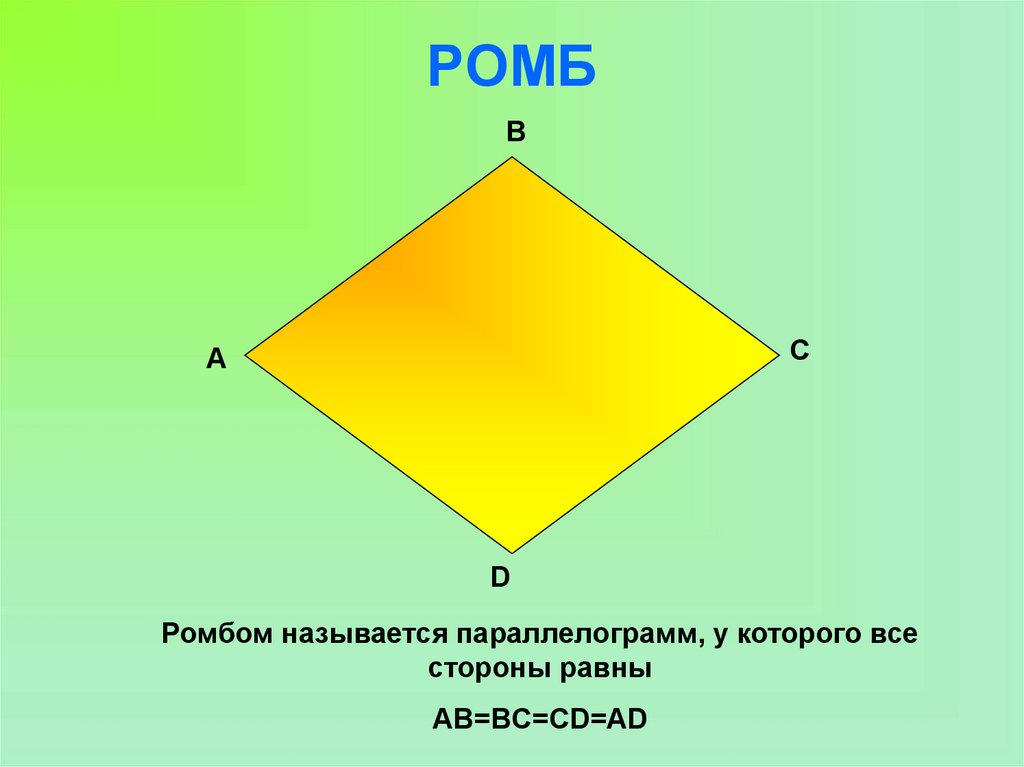
9. РОМБ
BC
A
D
Ромбом называется параллелограмм, у которого все
стороны равны
AB=BC=CD=AD
10.
BC
A
D
Диагонали ромба взаимно перпендикулярны и делят
его углы пополам
AC ┴ BD, <BAO = <DAO
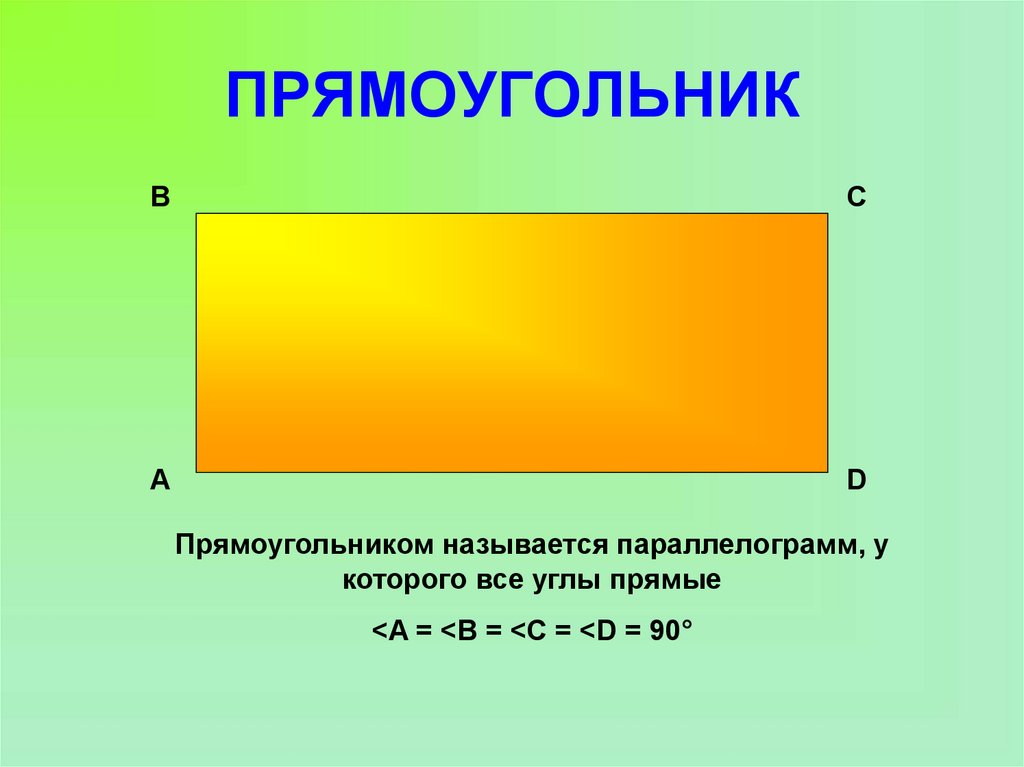
11. ПРЯМОУГОЛЬНИК
BC
А
D
Прямоугольником называется параллелограмм, у
которого все углы прямые
<A = <B = <C = <D = 90°
12.
BC
А
D
Диагонали прямоугольника равны
AC = BD
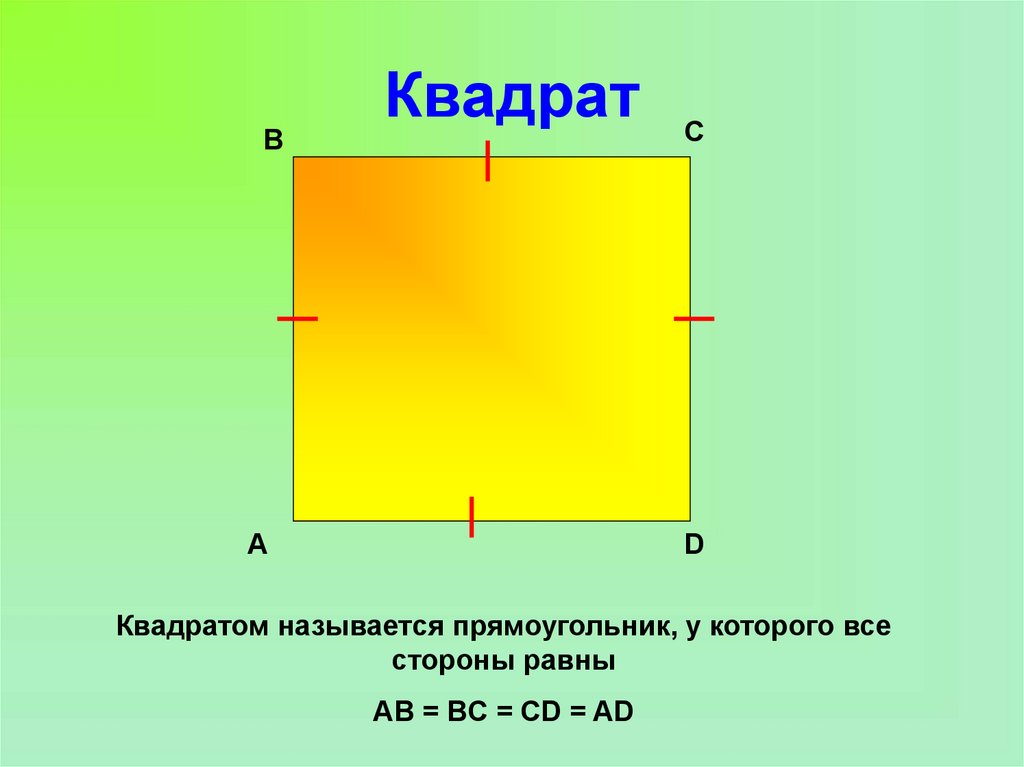
13. Квадрат
ВКвадрат
А
С
D
Квадратом называется прямоугольник, у которого все
стороны равны
AB = BC = CD = AD
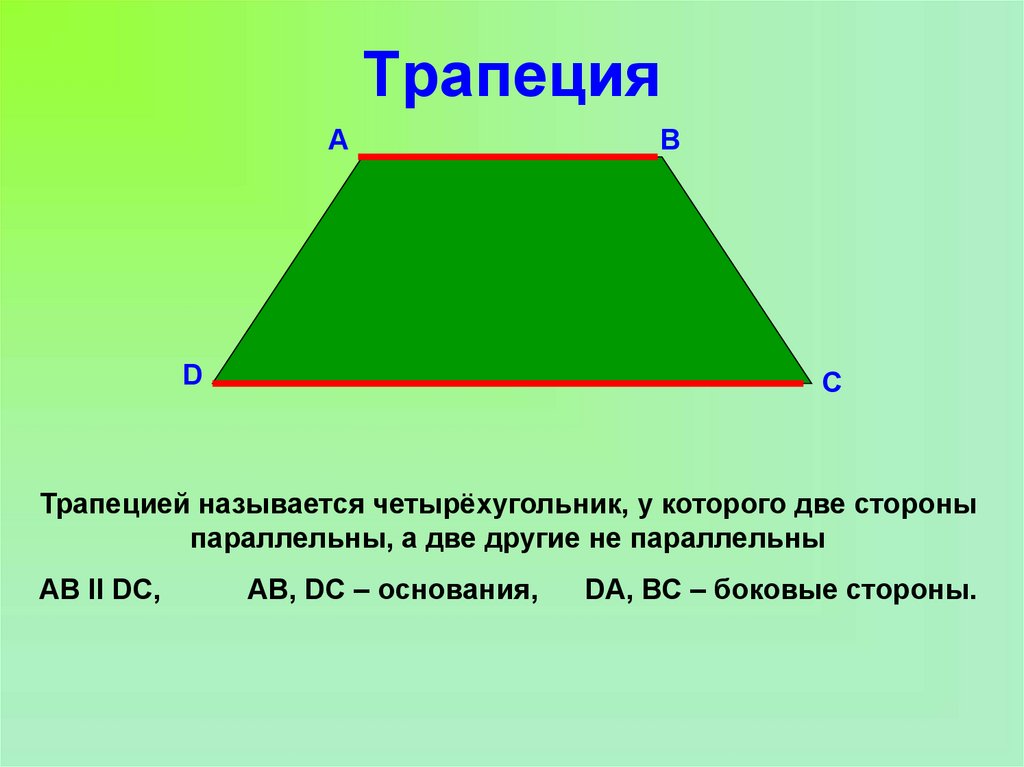
14. Трапеция
АD
В
С
Трапецией называется четырёхугольник, у которого две стороны
параллельны, а две другие не параллельны
АВ ІІ DC,
АВ, DC – основания,
DА, ВС – боковые стороны.
15.
ВВ
С
А
D
Трапеция называется
равнобедренной, если ее
боковые стороны равны.
АВ = СD
С
А
D
Трапеция, один из углов
которой прямой,
называется
прямоугольной
<А =90°
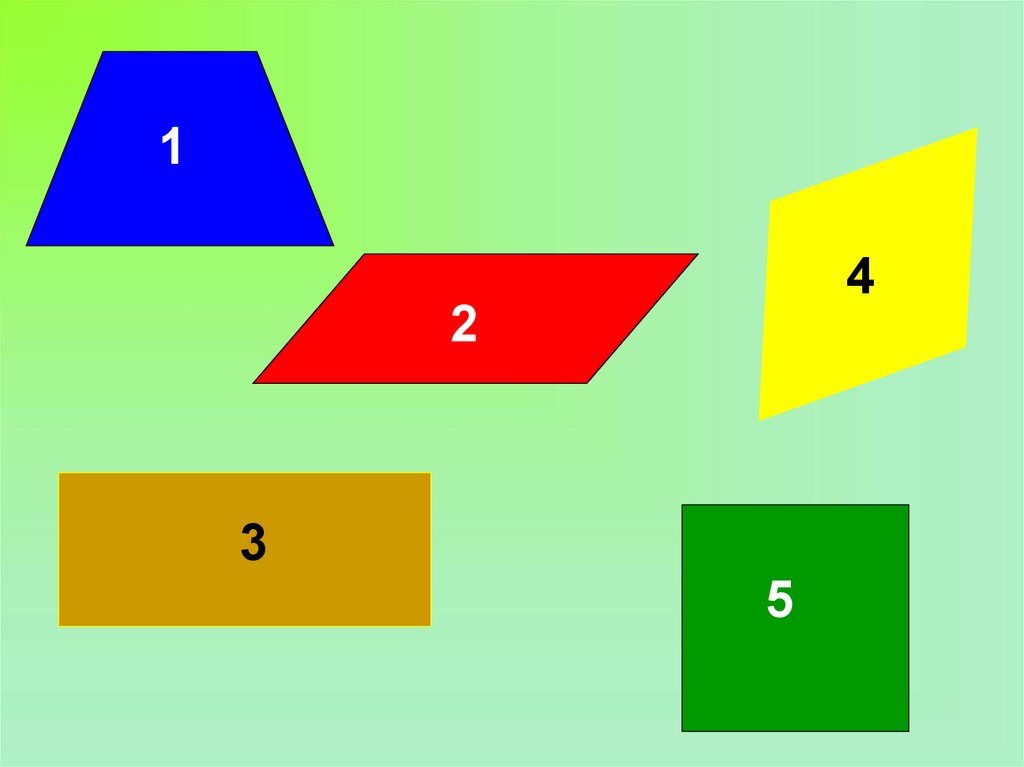
16.
14
2
3
5
17. ТЕСТИРОВАНИЕ
1. Если диагонали у параллелограмма равны, то он может быть:а)квадратом, б)квадратом или прямоугольником,
в)прямоугольником, г)любым четырехугольником.
2. Если у параллелограмма диагонали пересекаются под прямым
углом, то он может быть:
а)ромбом, б)ромбом или квадратом, в)любым прямоугольником.
3. Чему равна сумма углов параллелограмма:
А)180°, б)90°, в)360°, г)720°.
4. Если одна сторона параллелограмма равна 10 см, а другая –
20 см, то периметр его равен:
а)10 см, б)20 см, в)30 см, г)60 см, д)120 см.
18.
5. Если стороны параллелограмма равны 3 см и 5 см, то какие этостороны:
а) соседние, б)противоположные, в)любые.
6. Если один угол параллелограмма равен 42°, то чему равны
другие его углы:
А)42° и 82°, б)42°, 84°, 54°, в)42°, 138°, 138°, г) 84°, 138°.
7. Сумма двух углов параллелограмма равна 100°. Какие это углы:
а)соседние, б)противоположные, в)любые.
8. Если диагональ параллелограмма образует с его сторонами
углы 30° и 40° , то углы параллелограмма равны:
а)60°, 80°,б)70°,10°, в)70°, 110°
9. Если одна диагональ ромба равна его стороне, то чему будут
равны углы ромба:
а)60°, б)90°, в)60°, 120°.
19. Проверка
1.2.
3.
4.
5.
6.
7.
8.
9.
б)квадратом или прямоугольником.
б)ромбом или квадратом.
в)360°.
г)60 см.
а) соседние.
в)42°, 138°, 138°.
б)противоположные.
в)70°, 110°.
в)60°, 120°.
20. Решение задач
Задача 1.Меньшая сторона прямоугольника равна 4 см и образует с диагональю
угол в 60°.Найдите диагонали прямоугольника.
Задача 2.
Сумма трёх углов параллелограмма равна 252°. Найдите углы
параллелограмма.
Задача 3.
Углы, образуемые стороной ромба с его диагоналями, относятся как
4:5. Вычислите углы ромба.
Задача 4.
Меньшая боковая сторона прямоугольной трапеции равна 8 см.
Острый угол равен 30°. Найти другую боковую сторону трапеции.
Задача 5.
Дан квадрат, сторона которого равна 1м. Диагональ его служит
стороной другого квадрата. Найдите диагональ последнего.
21.
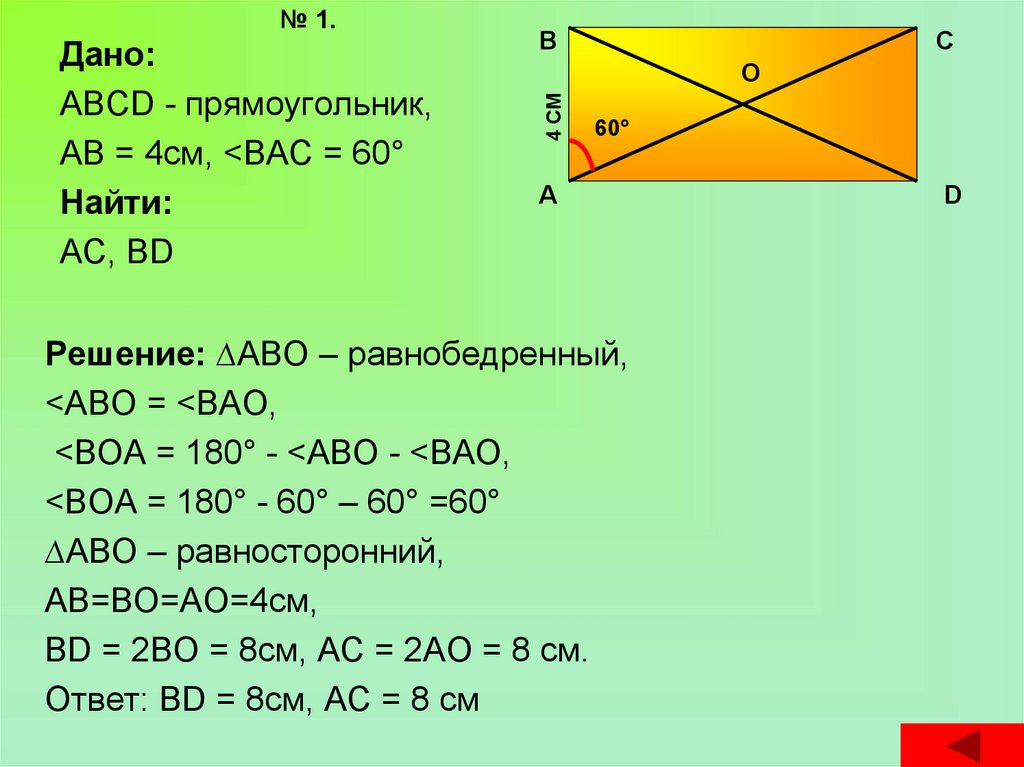
Дано:ABCD - прямоугольник,
АВ = 4см, <ВАС = 60°
Найти:
АС, BD
В
С
О
4 СМ
№ 1.
60°
А
Решение: ∆ABO – равнобедренный,
<АВО = <ВАО,
<ВОА = 180° - <АВО - <ВАО,
<ВОА = 180° - 60° – 60° =60°
∆ABO – равносторонний,
АВ=ВО=АО=4см,
ВD = 2ВО = 8см, АС = 2АО = 8 см.
Ответ: ВD = 8см, АС = 8 см
D
22.
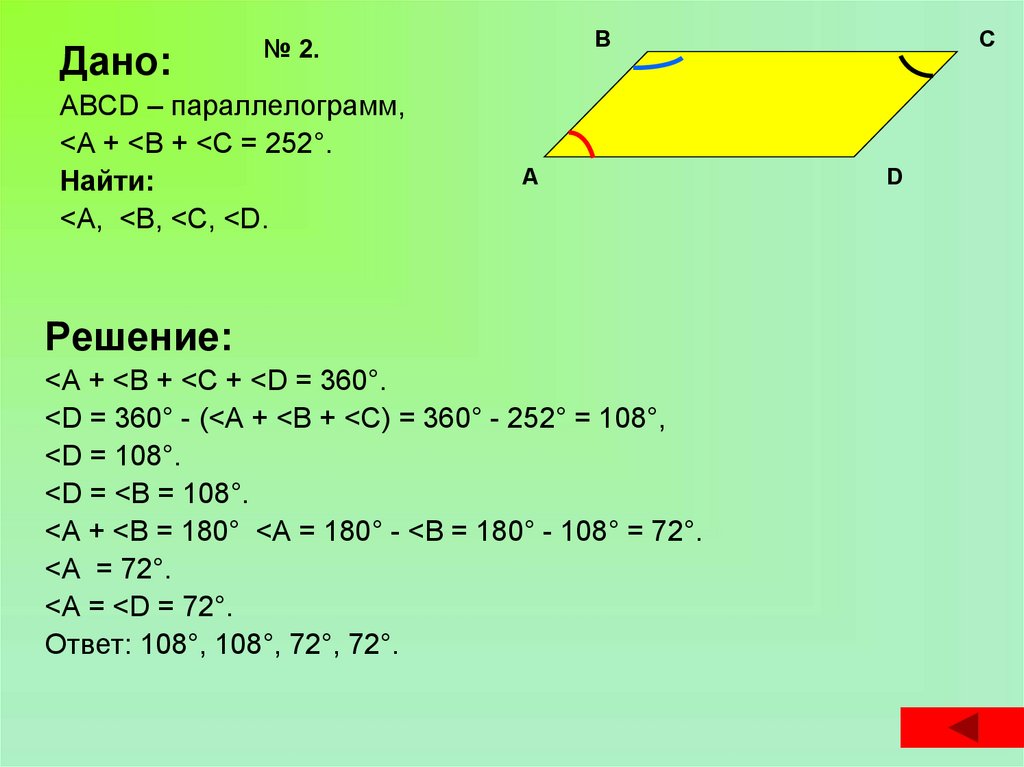
Дано:В
№ 2.
ABCD – параллелограмм,
<А + <В + <С = 252°.
Найти:
<А, <В, <С, <D.
А
Решение:
<А + <В + <С + <D = 360°.
<D = 360° - (<А + <В + <С) = 360° - 252° = 108°,
<D = 108°.
<D = <В = 108°.
<А + <В = 180° <А = 180° - <В = 180° - 108° = 72°.
<А = 72°.
<А = <D = 72°.
Ответ: 108°, 108°, 72°, 72°.
С
D
23.
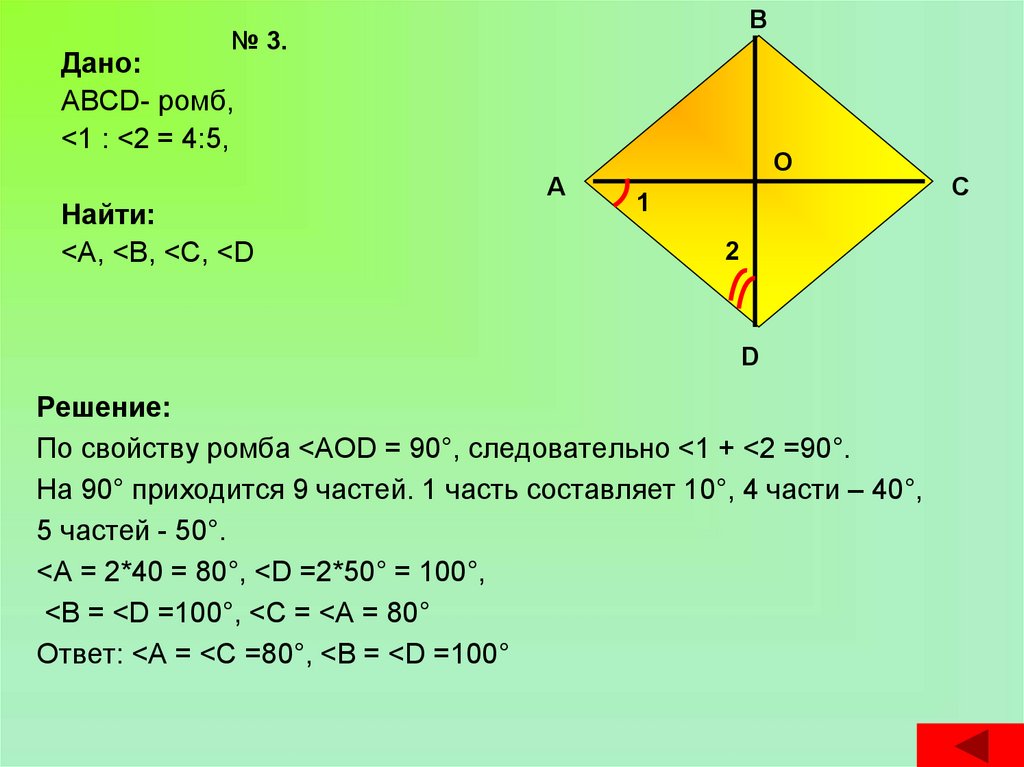
В№ 3.
Дано:
ABCD- ромб,
<1 : <2 = 4:5,
Найти:
<А, <В, <С, <D
А
О
1
2
D
Решение:
По свойству ромба <АОD = 90°, следовательно <1 + <2 =90°.
На 90° приходится 9 частей. 1 часть составляет 10°, 4 части – 40°,
5 частей - 50°.
<А = 2*40 = 80°, <D =2*50° = 100°,
<В = <D =100°, <С = <А = 80°
Ответ: <А = <С =80°, <В = <D =100°
С
24.
Дано:АВСD –трапеция,
<А = 90°, АВ = 8 см,
<D= 30°
Найти:
CD
Решение:
В
С
8 см
№ 4.
30°
А
построим СК ┴ АD, СК = АВ = 8см
∆СDК – прямоугольный,
По свойству прямоугольного треугольника:
СК = ½ СD, СD = 2*8 =16 (см)
Ответ: СD = 18 см.
D
К
25.
№ 5.С
В
D
А
N
М
26.
№ 407 (геометрия 7-9 кл. Атанасян и др.)Острый угол ромба равен 30°. Найти высоту ромба, если
его периметр равен 16 см.
Длины оснований прямоугольной трапеции равны
10 и 6 см. Больший угол равен 120°. Найти большую
боковую сторону трапеции.
27.
28. Использованная литература:
1. Геометрия 7-9 кл, Атанасян и др;2. Журнал «Математика в школе»














 mathematics
mathematics








