Similar presentations:
Применение интересных свойств трапеции при решении задач
1.
2.
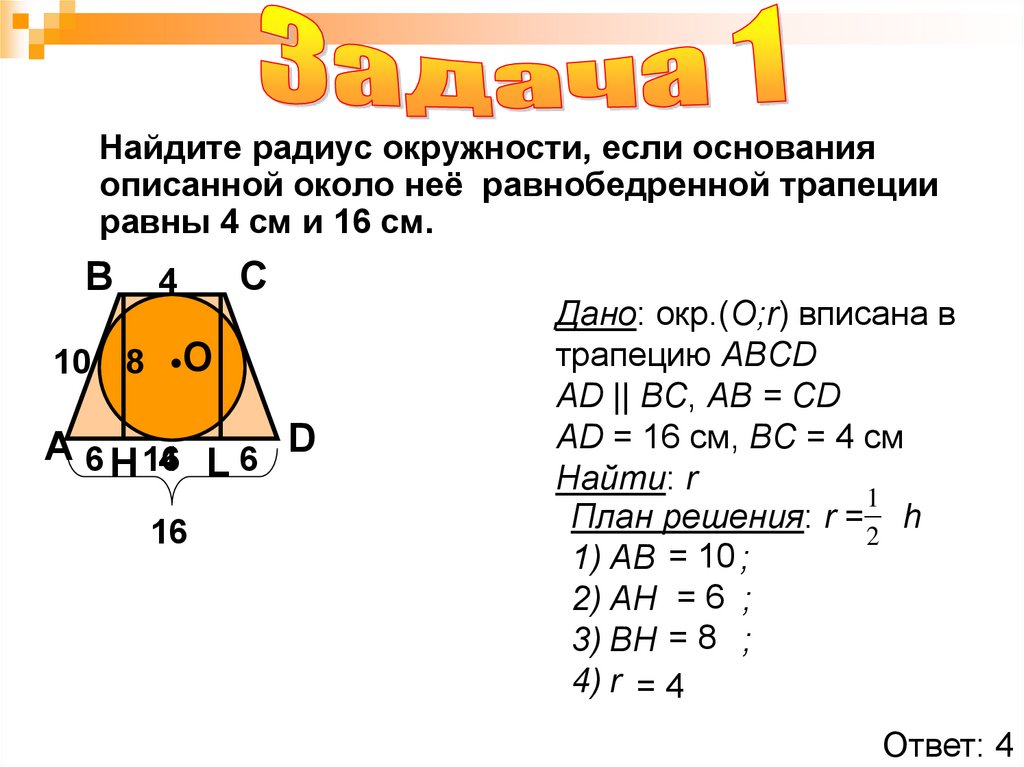
Найдите радиус окружности, если основанияописанной около неё равнобедренной трапеции
равны 4 см и 16 см.
B
10
С
4
8
O
D
A 6 H 16
4 L6
16
Дано: окр.(О;r) вписана в
трапецию ABCD
AD || BC, AB = CD
AD = 16 cм, ВС = 4 см
Найти: r
1
План решения: r = h
2
1) АВ = 10 ;
2) АН = 6 ;
3) ВН = 8 ;
4) r = 4
Ответ: 4
3.
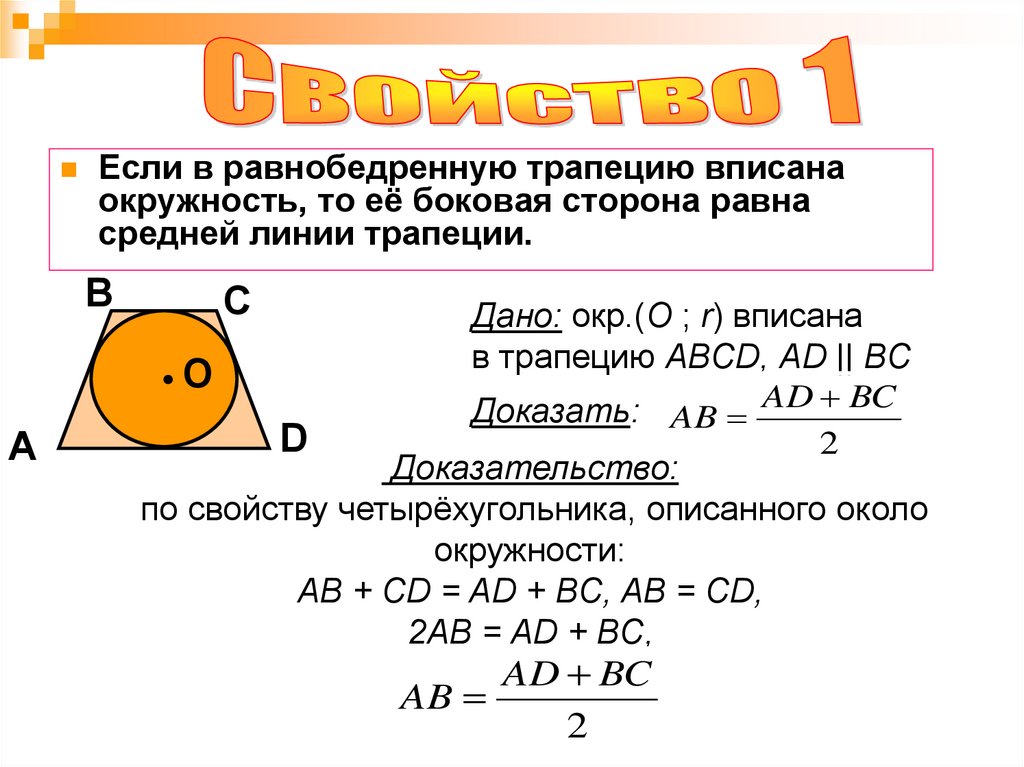
Если в равнобедренную трапецию вписанаокружность, то её боковая сторона равна
средней линии трапеции.
B
A
С
Дано: окр.(О ; r) вписана
в трапецию ABCD, AD || BС
О
Доказать: AB AD BC
D
2
Доказательство:
по свойству четырёхугольника, описанного около
окружности:
AB + CD = AD + BC, AB = CD,
2AB = AD + BC,
AD BC
AB
2
4.
Высота равнобедренной трапеции, в которуюможно вписать окружность, является средним
геометрическим её оснований: h 2 a b .
B
Дано: окр.(О ; r) вписана
в трапецию ABCD
AD || BС
AB = CD, BC = a, AD = b,
h – высота трапеции
2
Доказать: h a b
С
a
O
A
b
D
5.
Кa
B
a
N2
C
h
b
2
A
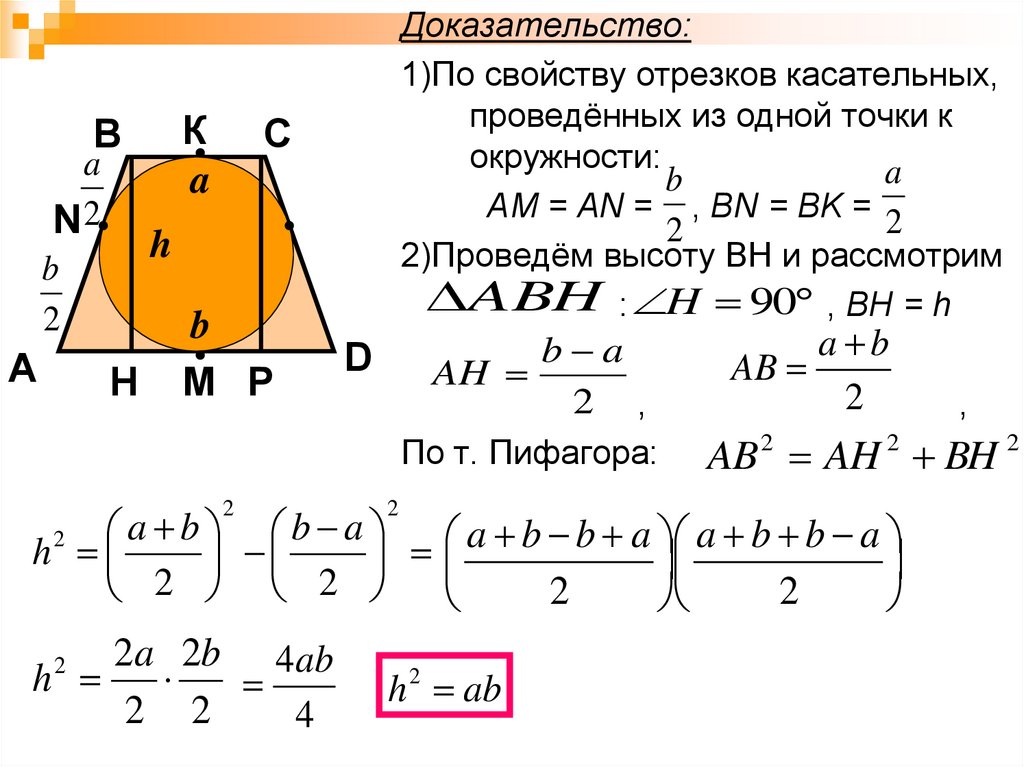
Доказательство:
1)По свойству отрезков касательных,
проведённых из одной точки к
окружности:
a
b
AM = AN = , BN = BK = 2
2
2)Проведём высоту ВН и рассмотрим
ABH : H 90 , ВН = h
H
b
M Р
b a
AH
2 ,
D
По т. Пифагора:
2
2
a b
AB
2
AB 2 AH 2 BH 2
a b b a a b b a a b b a
h
2
2
2
2
2a 2b 4ab
2
h
h 2 ab
2 2
4
2
,
6.
B4
Дано: окр.(О;r) вписана в
трапецию ABCD
AD || BC, AB = CD
AD = 16 cм, ВС = 4 см
Найти: r
1
Решение: r
h,
C
O
A
16
D
h =a∙b
2
h
2
16 4 4 2 8 (cм)
1
r 8 4 (cм)
2
Ответ: r = 4 см
7.
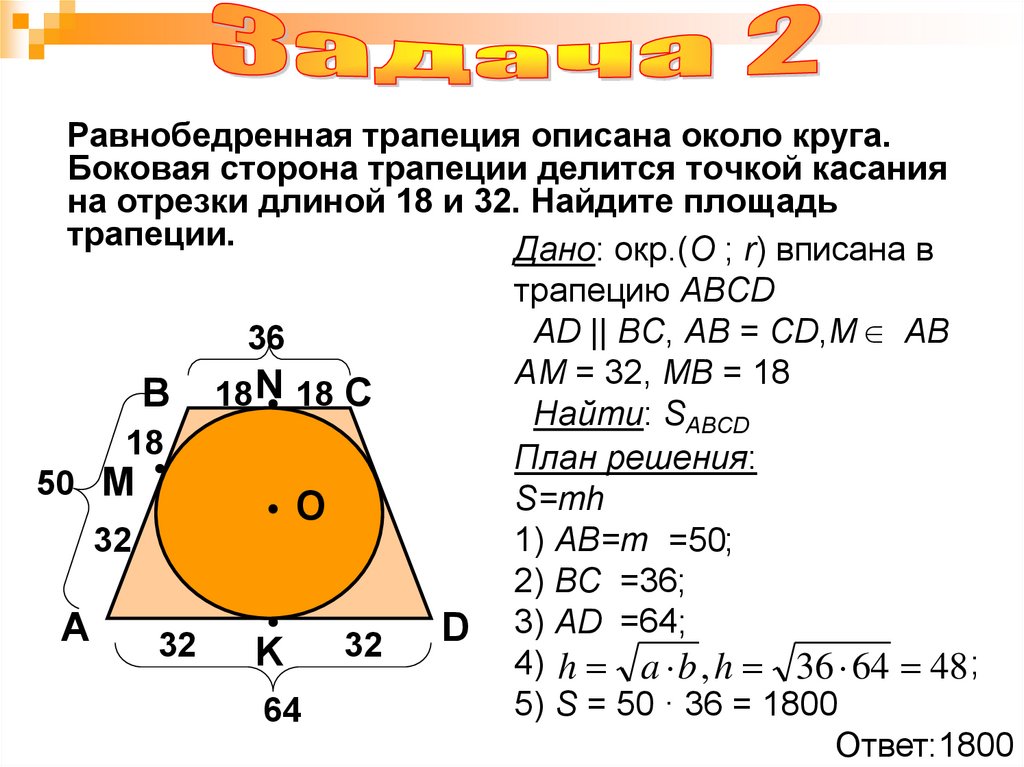
Равнобедренная трапеция описана около круга.Боковая сторона трапеции делится точкой касания
на отрезки длиной 18 и 32. Найдите площадь
трапеции.
Дано: окр.(О ; r) вписана в
трапецию ABCD
AD || BC, AB = CD,М АВ
36
AM = 32, MB = 18
N
B 18 18 C
Найти: SABCD
18
План решения:
50 M
S=mh
О
1) АВ=m =50;
32
2) ВС =36;
3) AD =64;
A
D
32
32
K
4) h a b , h 36 64 48 ;
5) S = 50 · 36 = 1800
64
Ответ:1800
8.
Найдите площадь равнобедренной трапеции, если еёдиагональ, равная 10, образует с основанием угол,
косинус которого равен
B
C
2 . (ЕГЭ- 2007, В11)
10
Дано: ABCD - трапеция, AD || BC
10
cos BDH = 2 , BD = 10
7 2
Найти: S 10
План решения: S = mh
A х
D
1) HD= 2 ;
х
К
2
H
2) ВН = 7 2 ;
3) АН = KD = x, m BC AD ,
2
AD 2 x AD 2 AD 2 x
m
AD x HD 2
2
2
4) S = 2 7 2 14
Ответ: 14
9.
В равнобедренной трапеции проекция диагонали набольшее основание равна средней линии трапеции.
B
A
H
C
К
D
Дано: ABCD- трапеция, BC || AD,
AB = CD,ВН AD, BD- диагональ
AD BC
Доказать: HD
2
Доказательство:
1) Опустим высоту СК.
AD HK
2) AH
;
2
3) HD AD AH ,
AD BC
HD AD
,
2
AD BC
HD
.
2
10.
Найдите площадь равнобедренной трапеции, если еёдиагональ, равная 10, образует с основанием угол,
косинус которого равен
B
C
10
7 2
A
H
D
2
2.
10
Дано: ABCD - трапеция,
AD || BC
2
cos BDH =
, BD = 10
10
Найти: S
План решения: S = mh
1) HD= 2 ;
2) ВН =7 2 ;
3) S = 2 7 2 14
Ответ: 14
11.
Около круга радиуса r описана равнобедренная трапеция.Боковая сторона трапеции составляет с меньшим
основанием угол α. Найдите радиус круга, описанного
около трапеции.
Дано: ABCD- трапеция, AD || BC,
B
C
2r
О
описанная около окр.(О; r) и вписанная в
окр.(О1;R) AB = CD, B
Найти: R
BD
Решение: по теореме синусов 2 R
sin A
D
BH
BH
2r
A Н
1). A 180 , sin A
, AB
,
AB
sin A sin
2r
2). AB HD , HD
;
sin
2
2
2
r
2
r
1
sin
3).BD 2 BH 2 HD 2 , BD 2r 2
sin
sin
BD
r 1 sin 2
4).R
R
2 sin
sin 2
12.
В равнобедренной трапеции диагонали взаимноперпендикулярны. Найдите площадь трапеции,
основания которой равны 10 и 26.
Дано: ABCD- трапеция, AD || BC,
B 5 M5 C
AB = CD, AD = 26, BC = 10, AC
45° 45°
Найти: S
План решения: S = mh
О
45°
45°
A
13
1) m
45°
45°
K
13
4) S
BD
AD BC
2
2) Проведём высоту МК;
D 3) AK =OK = 13, BM = MO = 5, MK = 18
AD BC
MK ,
2
10 26
S
18 18 18 324
2
Ответ: S = 324.
13.
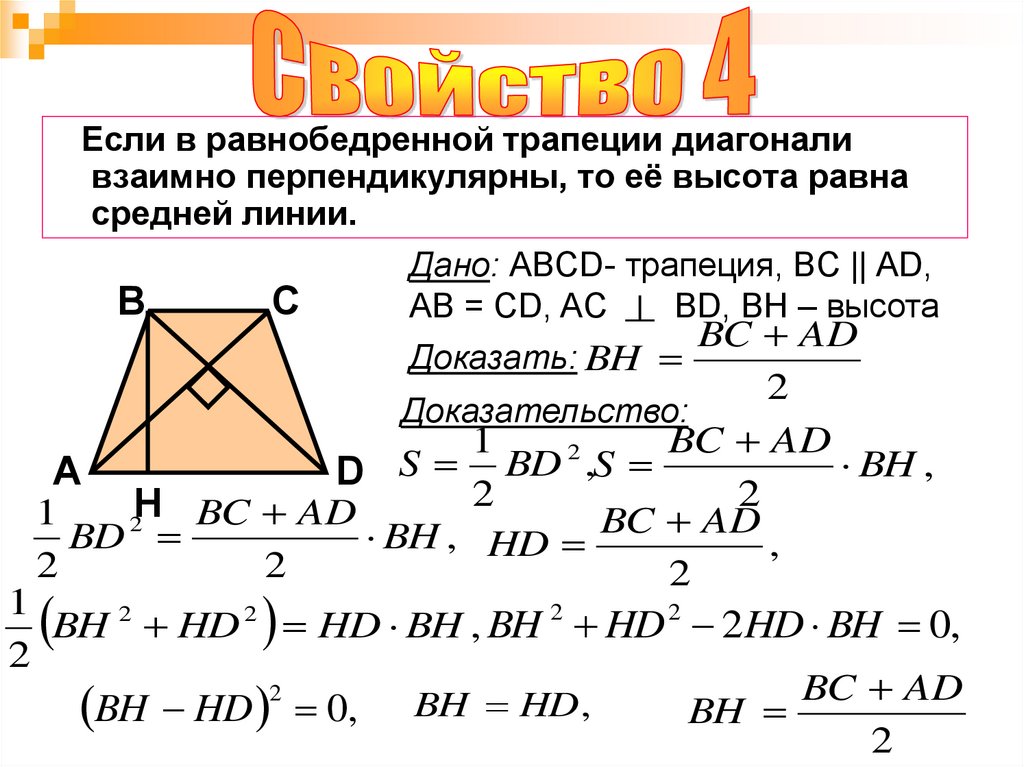
Если в равнобедренной трапеции диагоналивзаимно перпендикулярны, то её высота равна
средней линии.
B
С
Дано: ABCD- трапеция, BC || AD,
AB = CD, AC BD, BH – высота
BC AD
Доказать: BH
2
Доказательство:
1
BC AD
2
BH ,
A
D S BD ,S
2
2
Н
1
BC AD
2
BD
BH , HD BC AD ,
2
2
2
1
2
2
2
2
BH
HD
2 HD BH 0,
BH HD HD BH ,
2
BC AD
2
BH
HD
,
BH HD 0,
BH
2
14.
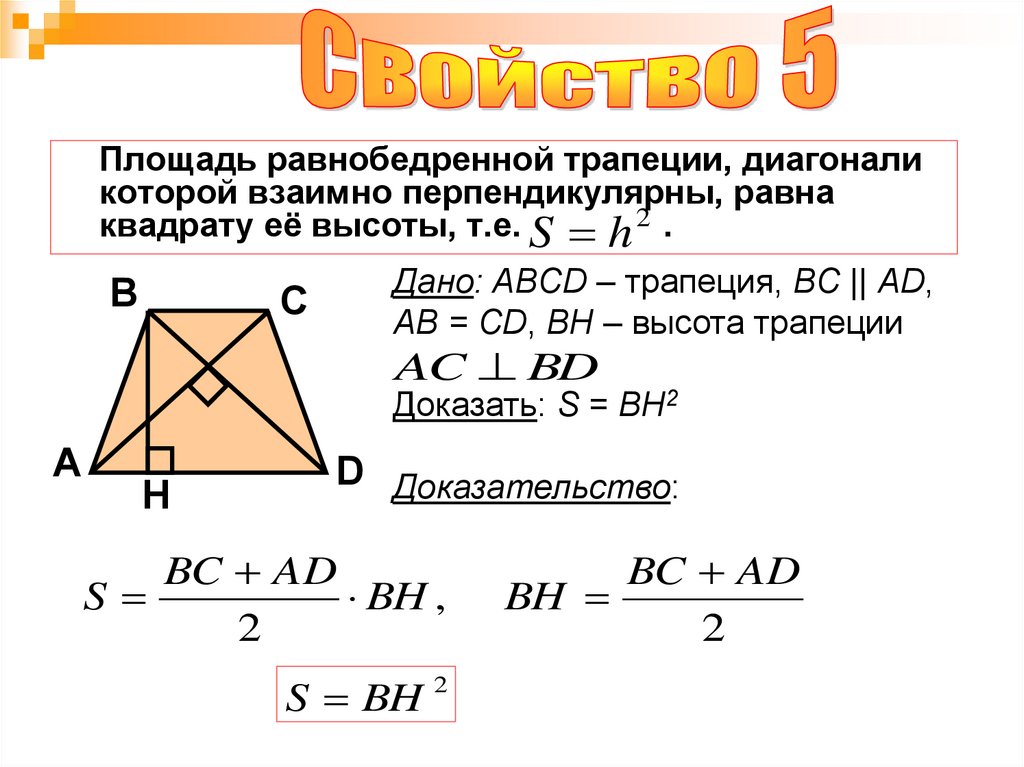
Площадь равнобедренной трапеции, диагоналикоторой взаимно перпендикулярны, равна
квадрату её высоты, т.е. S h 2 .
B
С
Дано: ABCD – трапеция, BC || AD,
AB = CD, BH – высота трапеции
AC BD
Доказать: S = BH2
A
Н
D Доказательство:
BC AD
S
BH ,
2
S BH 2
BC AD
BH
2
15.
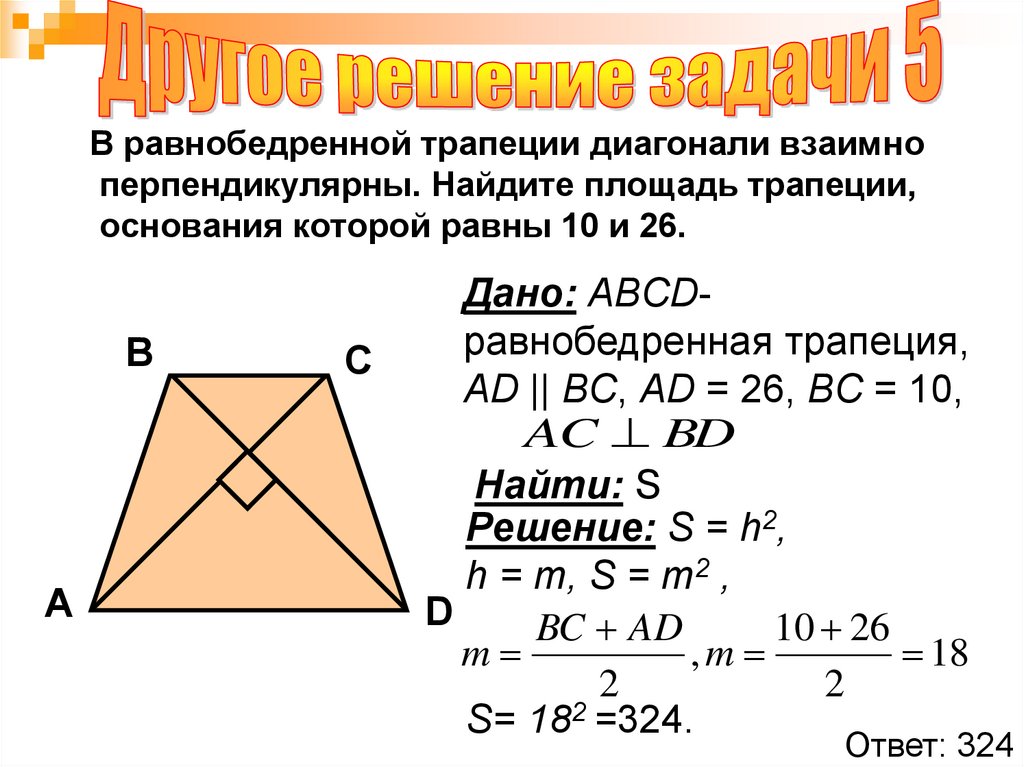
В равнобедренной трапеции диагонали взаимноперпендикулярны. Найдите площадь трапеции,
основания которой равны 10 и 26.
B
C
Дано: ABCDравнобедренная трапеция,
AD || BC, AD = 26, BC = 10,
AC BD
A
Найти: S
Решение: S = h2,
h = m, S = m2 ,
D
BC AD
10 26
m
,m
18
2
2
S= 182 =324.
Ответ: 324
16.
Сборник задач по математике для поступающих в вузы. Геометрия/Под ред. М.И.Сканави.- М.: Издательский дом ОНИКС: Альянс-В,
1999.
Зив Б.Г. ,Мейлер В.М. , Баханский А.Г. . Задачи по геометрии для 711 классов -М.: Просвещение, 1991.
Денищева Л.О., Глазков Ю.А., Краснянская К.А. и др. Учебнотренировочные материалы для подготовки к единому
государственному экзамену. Математика.- М: Интеллект- Центр,
2003-2008.
Кочагин В.В., Бойченко Е.М., Глазков Ю.А. и др. ЕГЭ- 2008:
математика: реальные задания.- М.: АСТ: Астрель, 2008.
Ковалева Г.И., Бузулина Т.И., Безрукова О.Л., Розка Ю.А.
Математика. Тренировочные тематические задания повышенной
сложности с ответами для подготовки к ЕГЭ и к другим формам
выпускного и вступительного экзаменов.- Волгоград: Учитель, 2007.
Симонов А.Я., Бакаев Д.С., Эпельман А.Г. и др. Система
тренировочных задач и упражнений по математике.- М.:
Просвещение, 1991.
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник
задач и контрольных работ по геометрии для 8 класса.- М.: Илекса,
Харьков: Гимназия, 1999.
Атанасян Л.С., Бутузов В.Ф. и др. Геометрия: Учеб. для 7-9 кл.
сред.шк.- М.: Просвещение, 2008.
Математика ЕГЭ- 2008. Вступительные испытания.Под ред.
Ф.Ф.Лысенко.- Ростов-на-Дону: Легион, 2008.
17.
18.
OR
Радиус окружности,
описанной около
трапеции, равен
радиусу окружности,
описанной около
треугольника,
вершины которого
лежат в вершинах
данной трапеции.











 mathematics
mathematics








