Similar presentations:
Адаптивные фильтры. Практическое применение (3)
1. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Адаптивные фильтры.Практическое
применение (3)
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)
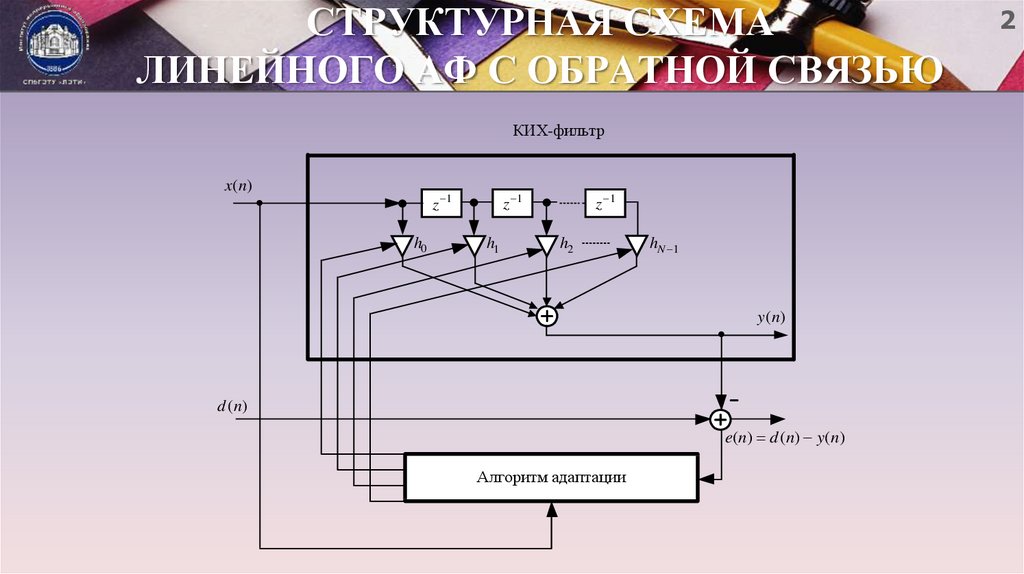
2. СТРУКТУРНАЯ СХЕМА ЛИНЕЙНОГО АФ С ОБРАТНОЙ СВЯЗЬЮ
КИХ-фильтрx ( n)
z 1
z 1
h0
h1
z 1
h2
hN 1
y ( n)
d ( n)
e( n ) d ( n ) y ( n )
Алгоритм адаптации
2
3. ЦЕЛИ ИССЛЕДОВАНИЯ
31) изучить метод идентификации многолучевого
канала связи при распространении сигнала от
источника к приемнику по нескольким трактам с
использованием структуры прямой идентификации;
2) выполнить компьютерное моделирование метода
идентификации многолучевого канала связи с
использованием программных средств MATLAB;
3) получить оценку импульсной характеристики
многолучевого канала связи.
4. ПРЯМАЯ ИДЕНТИФИКАЦИЯ НА ОСНОВЕ АФ
Схема прямой идентификацииНеизвестная
система
x(n)
Адаптивный
фильтр
d (n)
y(n)
e(n)
4
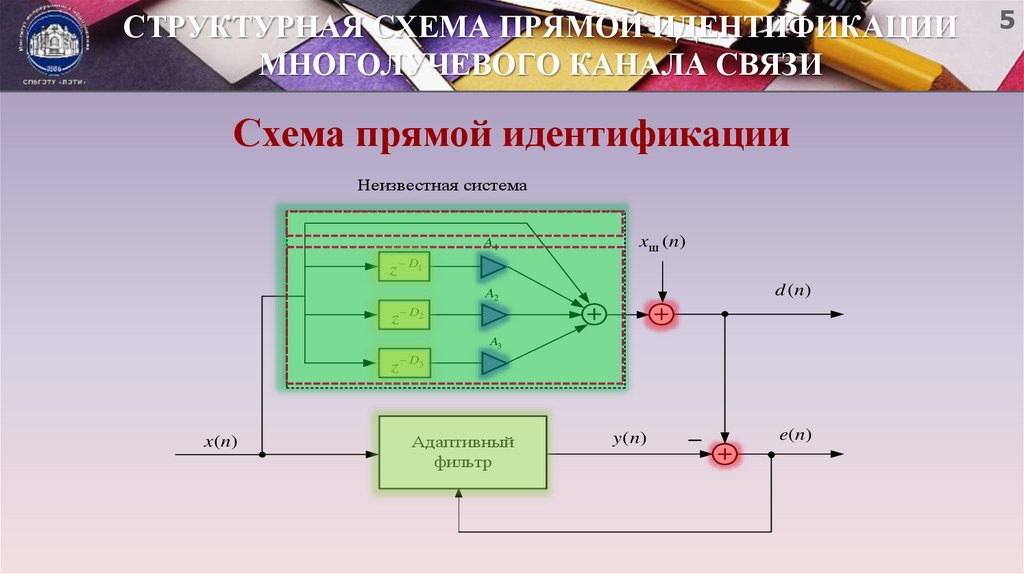
5. СТРУКТУРНАЯ СХЕМА ПРЯМОЙ ИДЕНТИФИКАЦИИ МНОГОЛУЧЕВОГО КАНАЛА СВЯЗИ
Схема прямой идентификацииНеизвестная система
A1
xш ( n)
z D1
d ( n)
A2
z D2
A3
z D3
x ( n)
Адаптивный
фильтр
y ( n)
e( n )
5
6. ТИПОВЫЕ СИГНАЛЫ ПРИ ИДЕНТИФИКАЦИИ МНОГОЛУЧЕВОГО КАНАЛА СВЯЗИ
61) x(n) – входной сигнал АФ и неизвестной системы;
2) xш(n) – шум среды распространения;
3) d(n) – смесь шума и выходного сигнала
неизвестной системы;
4) y(n) – выходной сигнал АФ;
5) e(n) – сигнал ошибки АФ.
7. АЛГОРИТМ ИДЕНТИФИКАЦИИ МНОГОЛУЧЕВОГО КАНАЛА СВЯЗИ
АЛГОРИТМ ИДЕНТИФИКАЦИИ МНОГОЛУЧЕВОГО 7КАНАЛА СВЯЗИ
1) Моделирование входного сигнала неизвестной системы – входного сигнала
АФ x(n) . Использовалась модель сигнала в виде случайной
последовательности чередующихся символов +1 и -1;
2) Вычисление образцового сигнала АФ (сумма выходного сигнала
неизвестной системы и шума среды распространения: d(n). Использовалась 4лучевая модель канала . Шум среды распространения – НБШ с m=0;
3) Вычисление истинной импульсной характеристики неизвестной системы
h(n);
4) Моделирование структуры АФ – объекта adaptfilt;
5) Моделирование адаптивной фильтрации: вычисление y(n) и e(n);
6) Определение параметров АФ – оценки импульсной характеристики h(n);
7) Сравнение истинной импульсной характеристики h(n) и ее оценки по
критерию среднего абсолютного отклонения (MAE – Mean Absolute Error).
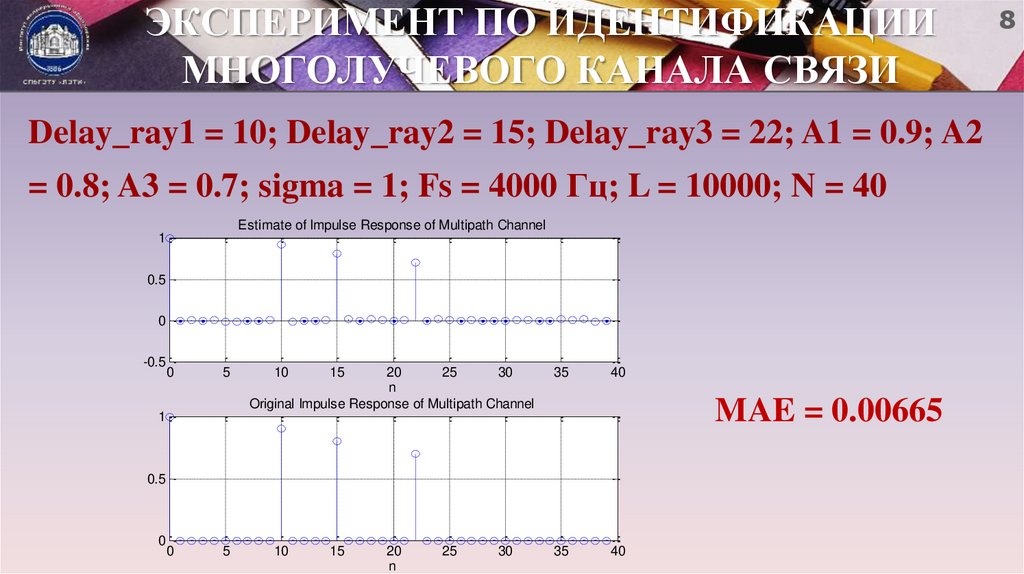
8. ЭКСПЕРИМЕНТ ПО ИДЕНТИФИКАЦИИ МНОГОЛУЧЕВОГО КАНАЛА СВЯЗИ
Delay_ray1 = 10; Delay_ray2 = 15; Delay_ray3 = 22; A1 = 0.9; A2= 0.8; A3 = 0.7; sigma = 1; Fs = 4000 Гц; L = 10000; N = 40
Estimate of Impulse Response of Multipath Channel
1
0.5
0
-0.5
0
5
30
25
20
n
Original Impulse Response of Multipath Channel
10
15
35
40
MAE = 0.00665
1
0.5
0
0
5
10
15
20
n
25
30
35
40
8
9. ПОДАВЛЕНИЕ УЗКОПОЛОСНОЙ ПОМЕХИ В ШИРОКОПОЛОСНОМ СИГНАЛЕ
Цель исследования:1) изучить метод подавления узкополосной помехи (УП-помехи) в
широкополосном сигнале (ШП-сигнале) на основе адаптивной
фильтрации с использованием структуры прямой идентификации.
2) выполнить компьютерное моделирование метода подавления
УП-помехи в ШП-сигнале в среде MATLAB;
3) исследовать качество подавления УП-помехи на основе
выбранных критериев;
4) выполнить компьютерное моделирование подавления УПпомехи в ШП-сигнале в MATLAB при различных моделях
сигналов.
9
10. ПРЯМАЯ ИДЕНТИФИКАЦИЯ НА ОСНОВЕ АФ
Схема прямой идентификацииНеизвестная
система
x(n)
Адаптивный
фильтр
d (n)
y(n)
e(n)
10
11. СТРУКТУРНАЯ СХЕМА ПРЯМОЙ ИДЕНТИФИКАЦИИ ПРИ ПОДАВЛЕНИИ УП-ПОМЕХИ В ШП-СИГНАЛЕ
СТРУКТУРНАЯ СХЕМА ПРЯМОЙ ИДЕНТИФИКАЦИИ ПРИ 11ПОДАВЛЕНИИ УП-ПОМЕХИ В ШП-СИГНАЛЕ
Схема прямой идентификации
Неизвестная система
xшп (n)
d (n) xуп (n) xшп (n)
x(n)
x(n) xуп (n)
Адаптивный
фильтр
y(n) xˆуп (n)
e(n) xˆшп (n)
12. ТИПОВЫЕ СИГНАЛЫ ПРИ ПОДАВЛЕНИИ УЗКОПОЛОСНОЙ ПОМЕХИ В ШИРОКОПОЛОСНОМ СИГНАЛЕ
ТИПОВЫЕ СИГНАЛЫ ПРИ ПОДАВЛЕНИИ УЗКОПОЛОСНОЙ 12ПОМЕХИ В ШИРОКОПОЛОСНОМ СИГНАЛЕ
1) x(n) – входной сигнал АФ и неизвестной системы;
2) xуп(n) – узкополосный сигнал; xшп(n) –
широкополосный сигнал; d(n) – смесь УП
(узкополосного) и ШП (широкополосного) сигналов;
3) y(n) – выходной сигнал АФ (оценка узкополосного
сигнала);
4) e(n) – сигнал ошибки АФ (оценка
широкополосного сигнала).
13. АЛГОРИТМ ПОДАВЛЕНИЯ УП-ПОМЕХИ В ШП-СИГНАЛЕ (1)
131) Моделирование входного сигнала неизвестной системы (узкополосного сигнала,
например, в виде гармонического сигнала из 2-х или 3-х гармоник) x(n) =xУП(n);
2) Моделирование широкополосного сигнала xШП(n) (например, в виде нормального
белого шума или ЛЧМ-сигнала);
3) Вычисление образцового сигнала АФ (сумма узкополосного и широкополосного
сигналов): d(n) = xУП(n) + xШП(n);
4) Моделирование структуры АФ с КИХ-фильтром (на основе объекта АФ);
5) Моделирование адаптивной фильтрации: вычисление y(n) ≈ xУП(n) и
e(n) ≈ xШП(n);
6) Сравнение сигналов xУП(n) и y(n) ≈ xУП(n) по среднеквадратическому критерию
(RMSE – Root Mean Squared Error);
7) Вычисление оценок математического ожидания и дисперсии нормального белого
шума e(n) ≈ xШП(n).
14. АЛГОРИТМ ПОДАВЛЕНИЯ УП-ПОМЕХИ В ШП-СИГНАЛЕ (2)
14Вывод графиков в MATLAB:
1) АКФ УП-помехи RУП(m) и ШП-сигнала RШП(m);
2) Входной сигнал АФ x(n) =xУП(n) и его ДПФ;
3) Образцовый сигнал d(n) и его ДПФ;
4) Выходной сигнал АФ y(n) ≈ xУП(n) и его ДПФ;
5) Оценки АКФ УП-помехи RУП(m) и ШП-сигнала RШП(m).
Используемые критерии:
RMSE:
RMSE
1 L 1
2
ˆ
x
(
n
)
x
(
n
)
2
2
L n 0
1 L 1
2
x
(
n
)
e
(
n
)
2
L n 0
15. ЭКСПЕРИМЕНТ
2 f12 f 2
xУП (n) A1 cos
n A2 cos
f
f
д
д
2 f3
n A3 cos
n
f
д
f д 4000Гц L 10000 длина сигнала
f1 100 Гц; f 2 120 Гц; f3 140 Гц частоты гармоник
A1 1; A2 0.5; A3 0.8 амплитуды гармоник
10 среднеквадратическое отклонение белого шума
N 40 порядок КИХ-фильтра в составе АФ
10.1179; M 0.10611 исходные оценки
15
16. АКФ УП-ПОМЕХИ И ШП-СИГНАЛА
ACF of Wideband Signal100
50
0
-50
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
m
ACF of Narrowband Signal
0.6
0.8
1
4
x 10
1
0.5
0
-0.5
-1
-1
-0.8
-0.6
-0.4
-0.2
0
m
0.2
0.4
0.6
0.8
1
4
x 10
16
17. ВХОДНОЙ СИГНАЛ АФ И ЕГО ДПФ
Input Signal of AF4
2
0
-2
-4
0
1000
2000
3000
4000
5000 6000
n
Amplitude Spectrum
7000
8000
9000
10000
1
0.5
0
0
500
1000
1500
2000
f
2500
3000
3500
4000
17
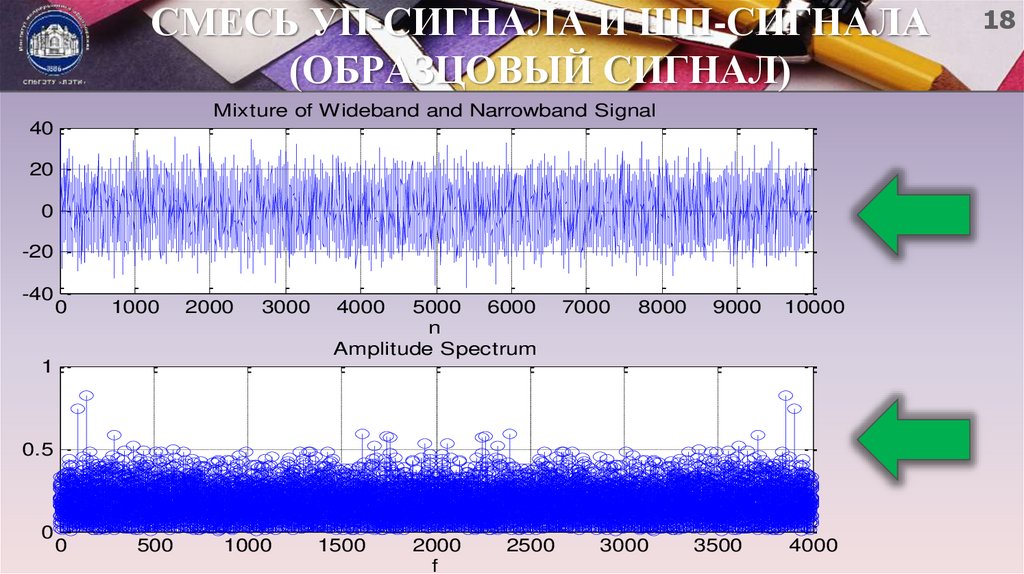
18. СМЕСЬ УП-СИГНАЛА И ШП-СИГНАЛА (ОБРАЗЦОВЫЙ СИГНАЛ)
Mixture of Wideband and Narrowband Signal40
20
0
-20
-40
0
1000
2000
3000
4000
5000 6000
n
Amplitude Spectrum
7000
8000
9000
10000
1
0.5
0
0
500
1000
1500
2000
f
2500
3000
3500
4000
18
19. ОЦЕНКА УП-ПОМЕХИ И ЕЕ ДПФ
Estimate of Narrowband Signal40
20
0
-20
-40
0
1000
9000
8000
7000
6000
5000
n
Amplitude Spectrum (Estimate of Narrowband Signal)
2000
3000
4000
10000
1
0.5
0
0
500
1000
1500
2000
f
2500
3000
3500
4000
19
20. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Адаптивные фильтры.Практическое
применение (3)
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)
















 mathematics
mathematics








