Similar presentations:
Определение абсолютной скорости и абсолютного ускорения точки
1. Расчетно-графическая работа №2
Задача К22. Определение абсолютнойскорости и абсолютного ускорения
точки.
Рисунок 3, вариант 11
2. Дано:
AB 10 смOC 12 см
3
sr ОМ f (t ) 12 2 (7t 2t ), см
t1 1 с
e (t ) 8t t 2 , рад
45 0
3. Найти:
Вычислить абсолютную скорости иабсолютное ускорение точки М в
момент времени t1 .
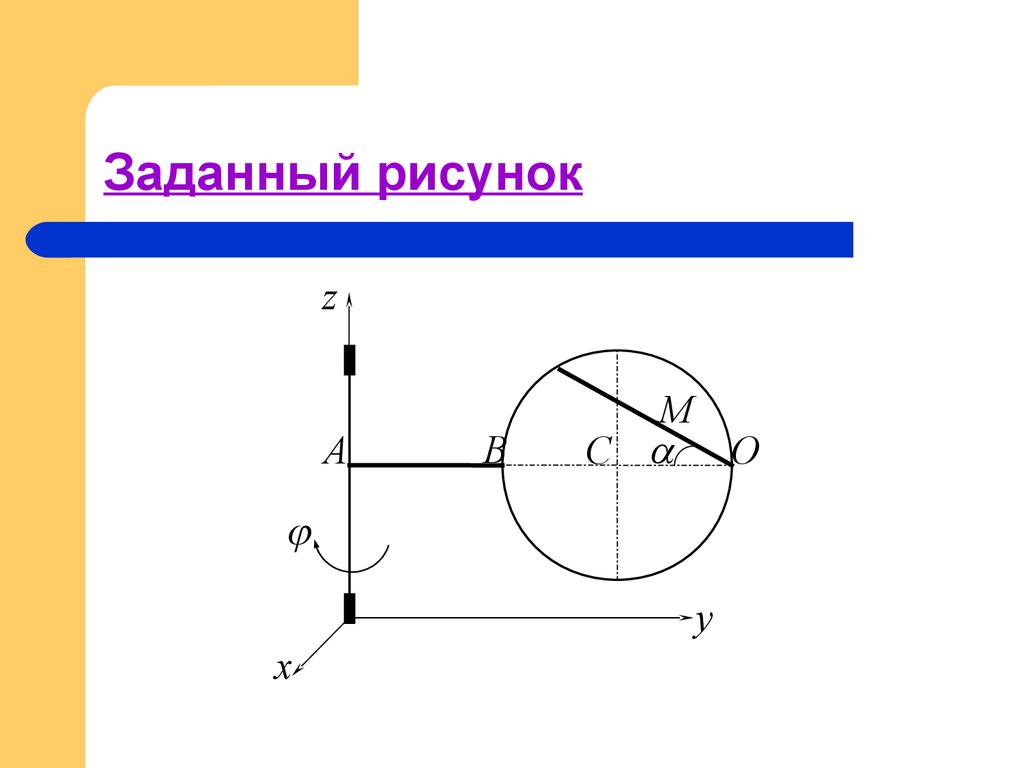
4. Заданный рисунок
zA
B
M
C O
y
x
5. Решение:
Точка М совершает сложное движение. Т.к.она движется по прямолинейному желобу
и одновременно желоб вместе с круглой
пластинкой вращается относительно оси
z.
Тогда абсолютная скорость v vr ve
и абсолютное ускорение w wr we wК .
6.
Определим положение точки М на рисунке.Для этого найдем, чему равно ее
перемещение в момент времени t1 :
sr (t1 ) OM 12 2 7 1 2 13 60 2 см
Сделаем рисунок с учетом всех условий и
при данном положении точки.
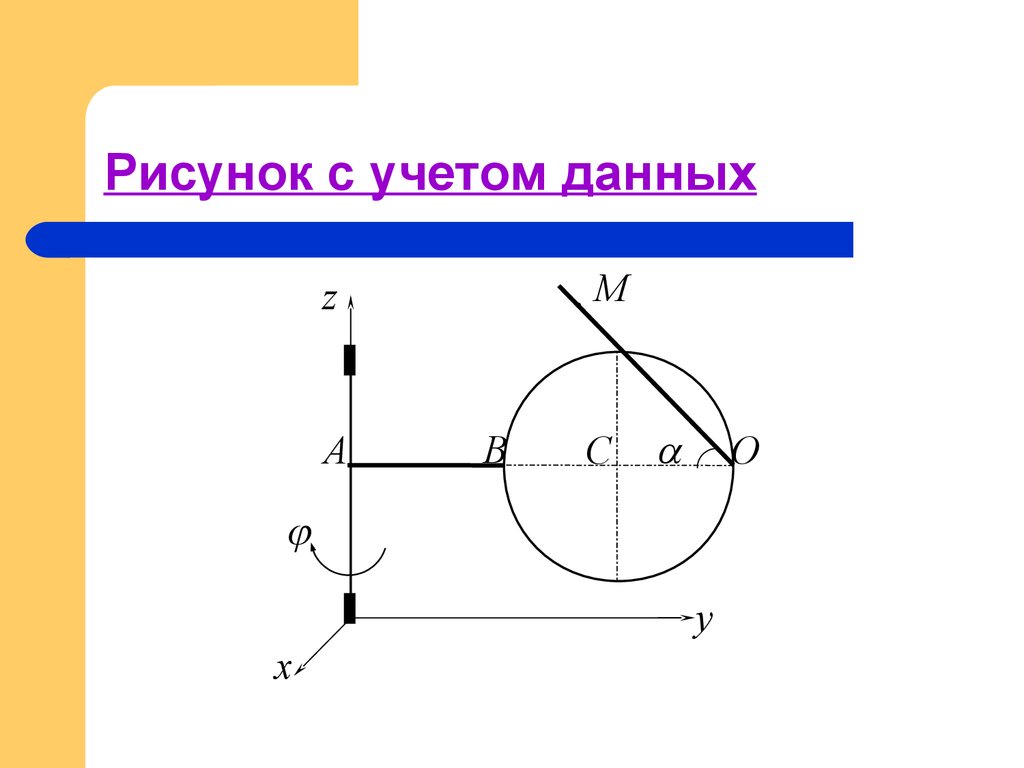
7. Рисунок с учетом данных
Mz
A
B
C
O
y
x
8. 1. Относительное движение точки М.
По условию задачи – движение т. М пожелобу – относительное.
Оно задано естественным способом.
Тогда скорость точки М:
vr s r 12 2 (7 6t 2 )
Ускорение точки М:
wr v r 12 2 ( 12t )
2
r
v
w
n
r
9.
Определим, чему равна скорость иускорение в момент времени t1 1 с
vr 12 2 см / с 0 - направление вектора
скорости совпадает с положительным
направлением движения.
w r 144 2 см / с 2 0 - направление вектора
касательного ускорения противоположно
положительному направлению движения.
2
12 2
n
wr
0
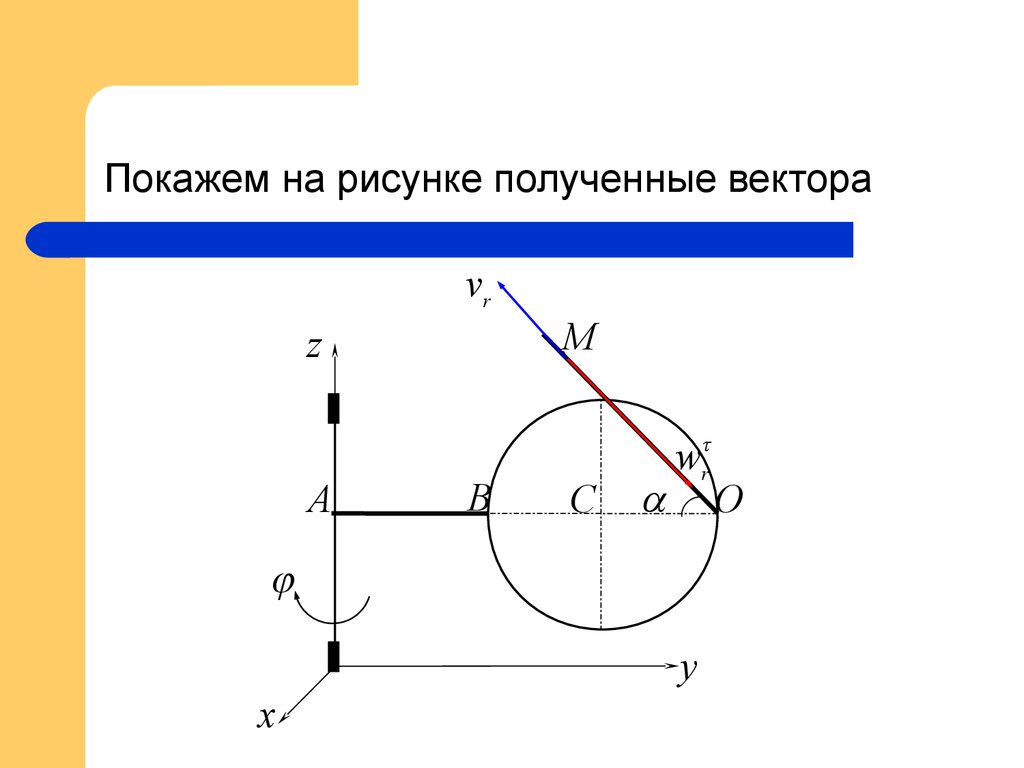
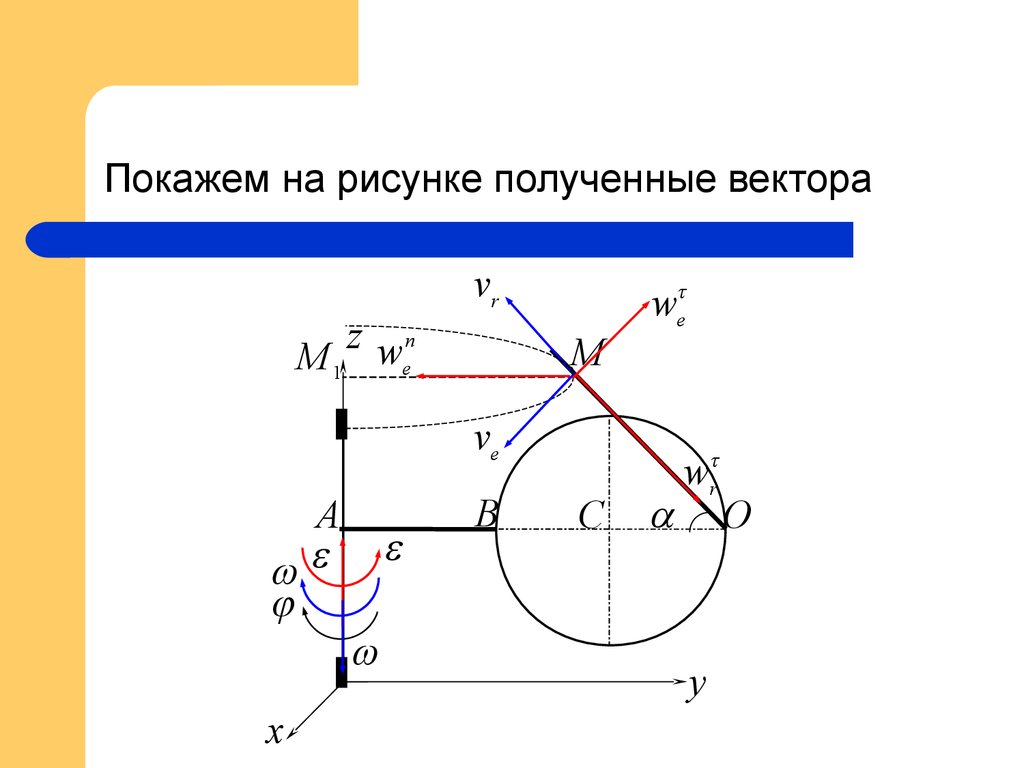
10. Покажем на рисунке полученные вектора
vrM
z
A
B
C
wr
y
x
O
11. 2. Переносное движение точки М.
По условию задачи – желоб вместе сдержавкой АВ вращается вокруг
неподвижной оси.
Т.е. переносное движение – вращательное.
12.
Определим угловую скорость и угловое ускорениеe 8 2t
2
Тогда при t1 1 с
6 с 1 0 - направление угловой скорости
совпадает с положительным
направлением угла поворота.
2 с 2 0 - направление углового
ускорения противоположно
положительному направлению угла
поворота
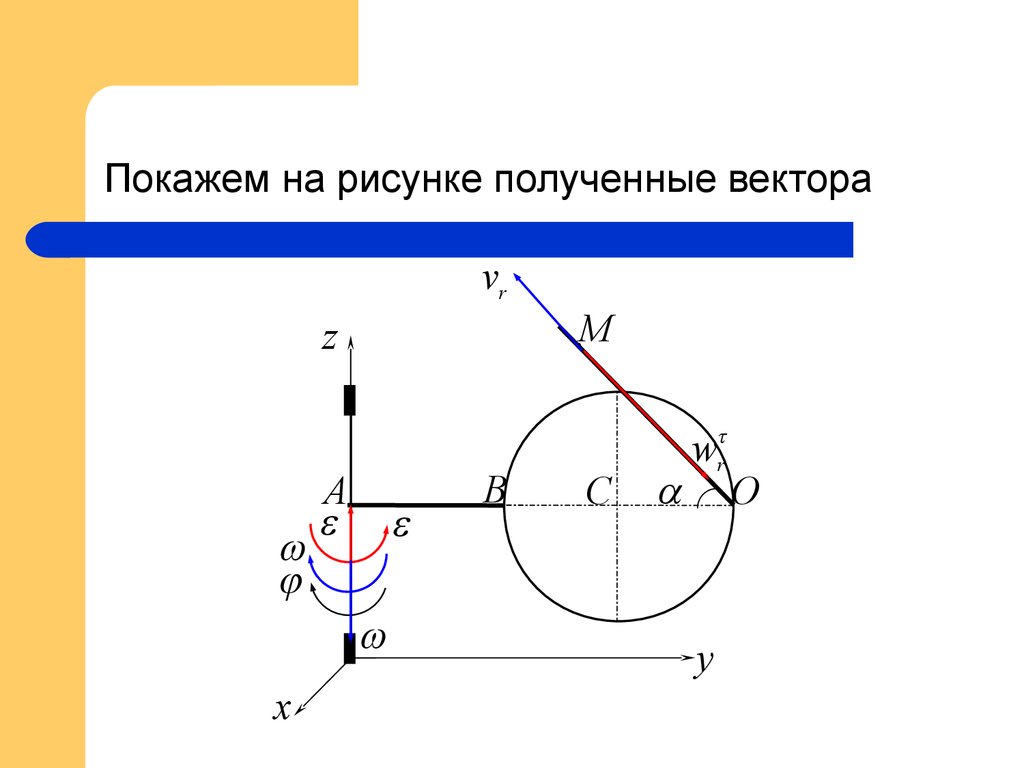
13. Покажем на рисунке полученные вектора
vrM
z
x
A
B
C
wr
y
O
14.
Для определения скорости и ускорениянеобходимо найти радиус вращения тела
в точке М – кратчайшее расстояние от
точки М до оси вращения:
MM 1 Re AB 2OC OM cos
2
10 2 12 60 2
26 см
2
15. Покажем на рисунке это расстояние
M1A
x
z
Re
vr
M
B
C
wr
y
O
16.
Определим скорость и ускорение точки М:ve MM 1 6 ( 26) 156 см / с - по
направлению угловой скорости
we MM 1 2 ( 26) 52 см / с 2 - по
направлению углового ускорения
wen 2 MM 1 62 ( 26) 936 см / с 2 - по
радиусу вращения к оси.
17. Покажем на рисунке полученные вектора
nzw
M1
e
vr
M
we
ve
A
x
B
C
wr
y
O
18. 3. Ускорение Кориолиса
Вычислим ускорение Кориолиса поформуле:
wК 2 vr sin( , vr ) 2 6 12 2 sin 1350 144 см / с 2
Направление вектора определим по правилу
правой руки или правилу Жуковского.
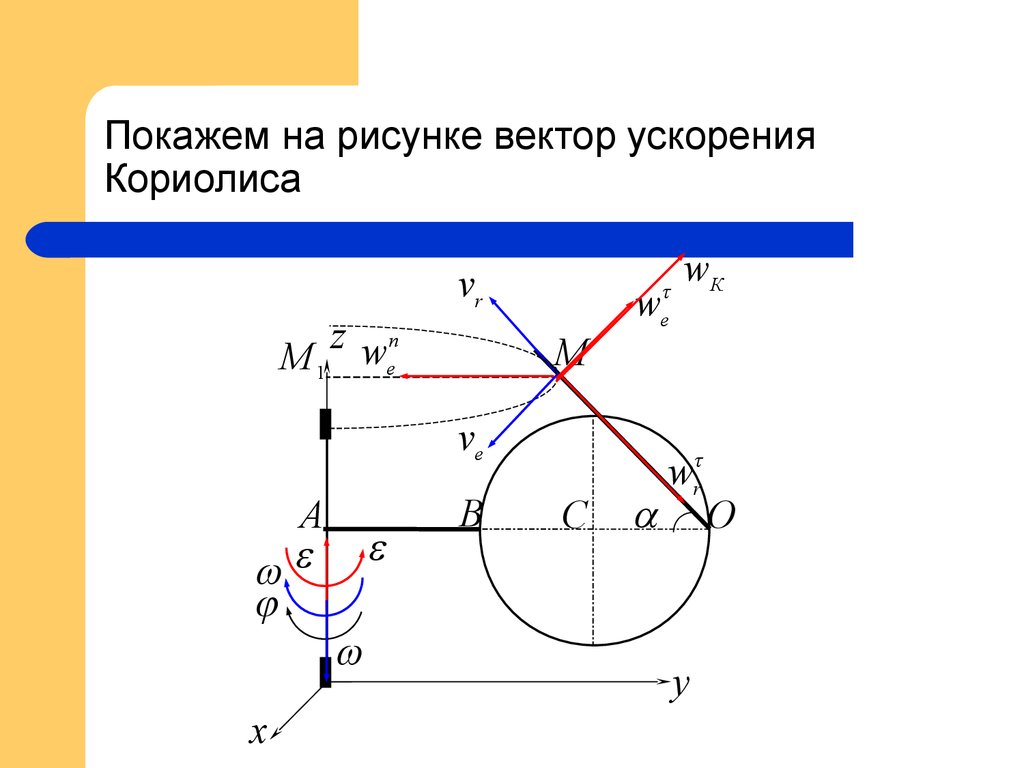
19. Покажем на рисунке вектор ускорения Кориолиса
nzw
M1
e
vr
M
wК
we
ve
A
x
B
C
wr
y
O
20. 4. Абсолютная скорость
Т.к. ve xИ vr ( y, z ) ,
то vr ve
Тогда абсолютная скорость равна:
v vr2 ve2 (12 2 ) 2 ( 156) 2 156,92 см / с
21. 5. Абсолютное ускорение.
Абсолютное ускорение можно представить вn n
виде: w wr wr we we wk
Спроецируем этот вектор на оси координат:
wx we wК 52 144 92
wy wen w r cos 450 936 144 1080
wz wr sin 45 144
Тогда:
w wx2 wy2 wz2 1093,435 см / с 2
22. Ответ:
v 156,92 см / сw 1093,435 см / с 2
















 physics
physics








