Задачи на построение

1.

1

2. Способы построения окружности

2

3.

Окружностью
называется
геометрическая фигура, состоящая из всех
точек,
расположенных
на
заданном
расстоянии от данной точки.
3

4.

Отрезок
соединяющий
две центр
точки
окружности,точку
Любой
соединяющий
какую-нибудь
Хорда, отрезок,
проходящая
через
окружности,
называется
хордой
окружности
сдиаметром
ее
центром, называется радиусом
называется ее
окружности
(O,r) или (O,R)
4

5.

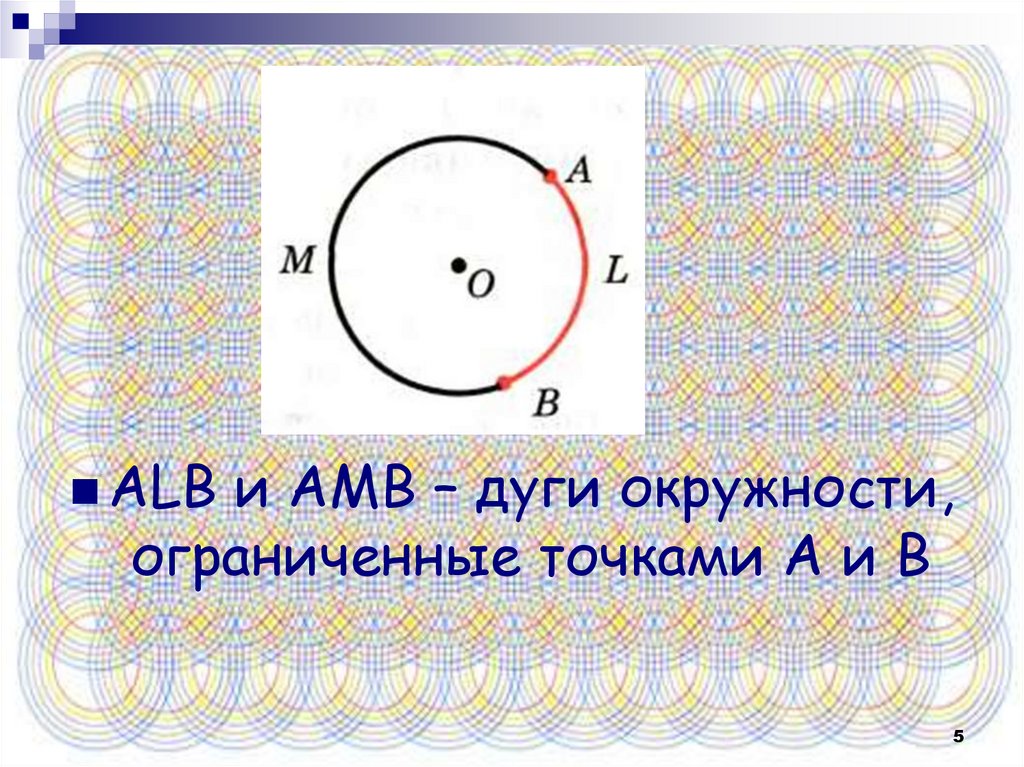
ALB
и AMB – дуги окружности,
ограниченные точками А и В
5

6.

С1
N
B
D1
O
T
S
M
P
D
C
A
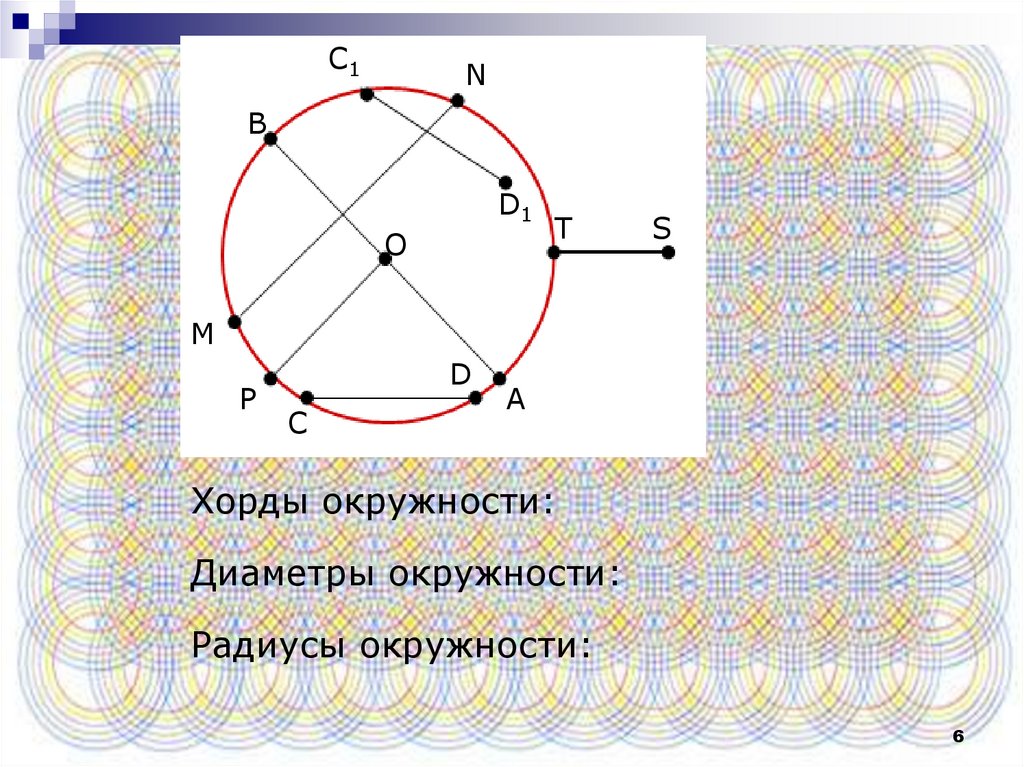
Хорды окружности:
Диаметры окружности:
Радиусы окружности:
6

7.

N
B
M
D
C
A
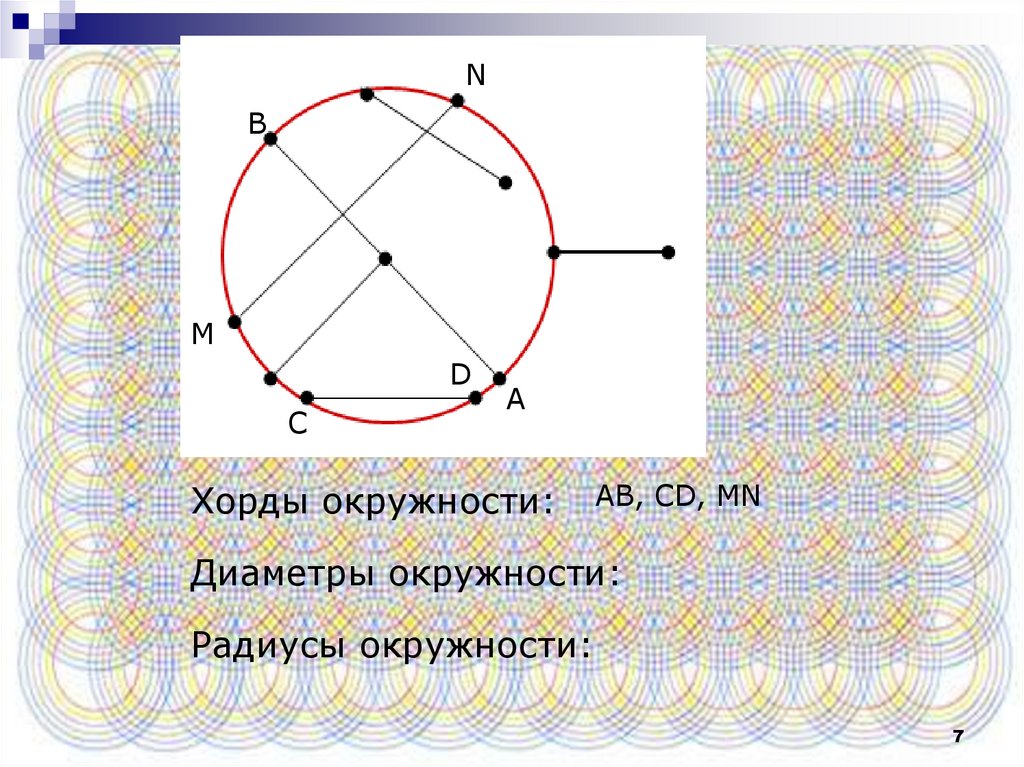
Хорды окружности:
AB, CD, MN
Диаметры окружности:
Радиусы окружности:
7

8.

B
O
A
Хорды окружности:
AB, CD, MN
Диаметры окружности:
AB
Радиусы окружности:
8

9.

B
O
P
A
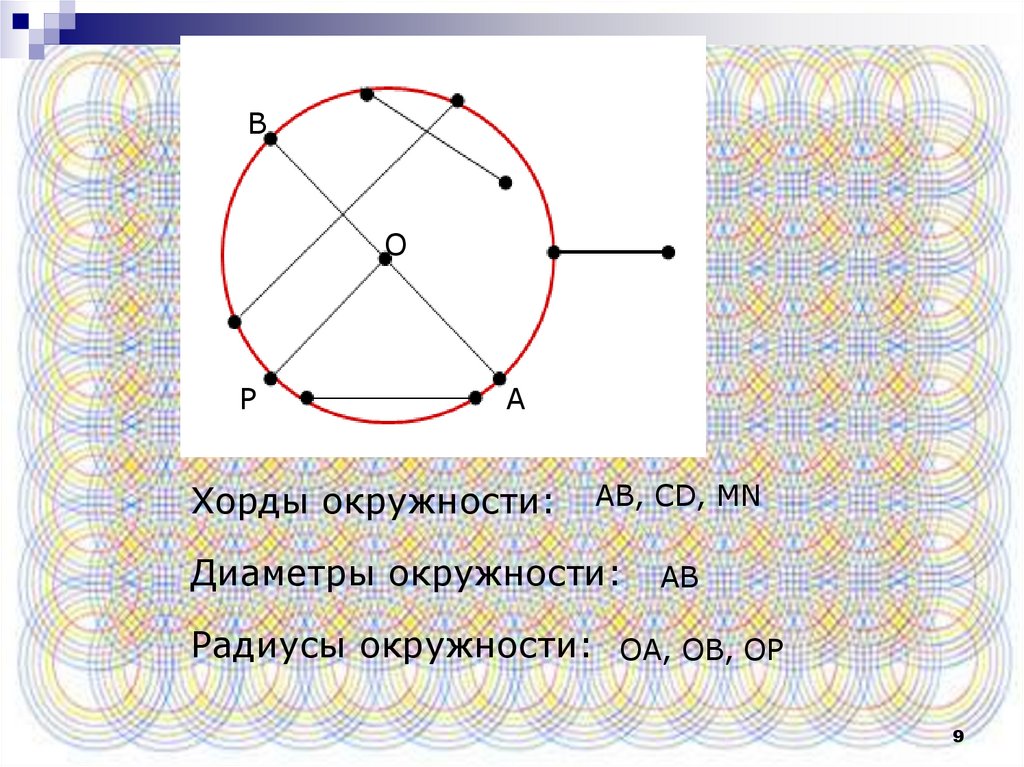
Хорды окружности:
AB, CD, MN
Диаметры окружности:
AB
Радиусы окружности: OA, OB, OP
9

10. Основные задачи на построение

Задача 1. На данном луче от его
начала отложить отрезок, равный
данному.
Задача 2. Отложить от данного луча
угол, равный данному.
Задача 3. Построить биссектрису
данного угла.
Задача 4. Построить прямую,
проходящую через данную точку и
перпендикулярную к данной прямой.
Задача 5. Построить середину
данного отрезка.
Задача 6. Построить прямую,
проходящую через точку, не
лежащую на данной прямой, и
перпендикулярную этой прямой.
10

11. Задача 1 С помощью циркуля и линейки без делений на данном луче отложить отрезок, равный данному

A
Дано: отрезок АВ
луч ОС
B
C
Построить: отрезок
ОD,OD=AB
O
11

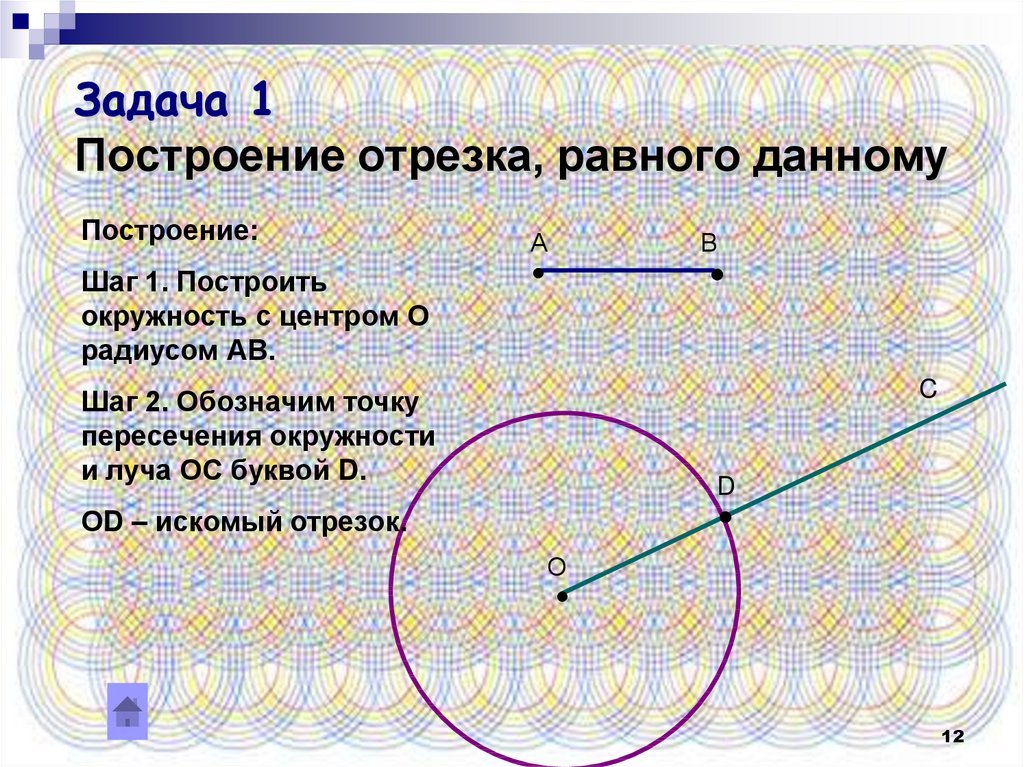
12. Задача 1 Построение отрезка, равного данному

Построение:
Шаг 1. Построить
окружность с центром О
радиусом АВ.
А
В
C
Шаг 2. Обозначим точку
пересечения окружности
и луча ОС буквой D.
D
ОD – искомый отрезок.
О
12

13.

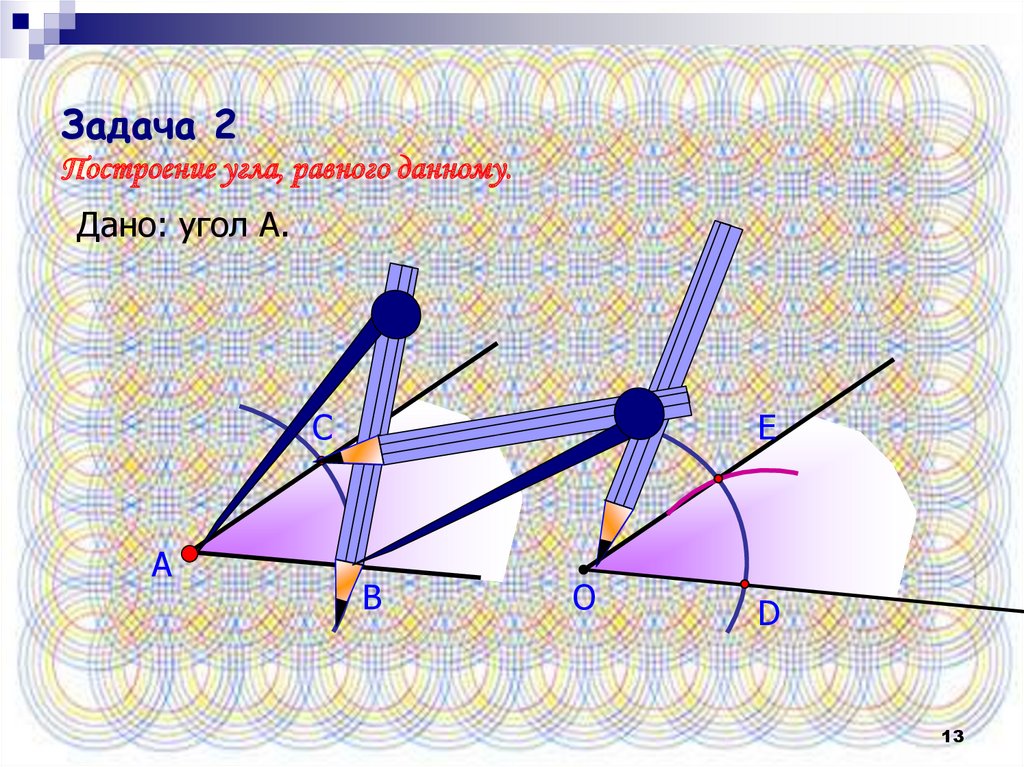
Задача 2
Построение угла, равного данному.
Дано: угол А.
С
А
E
В
О
D
13

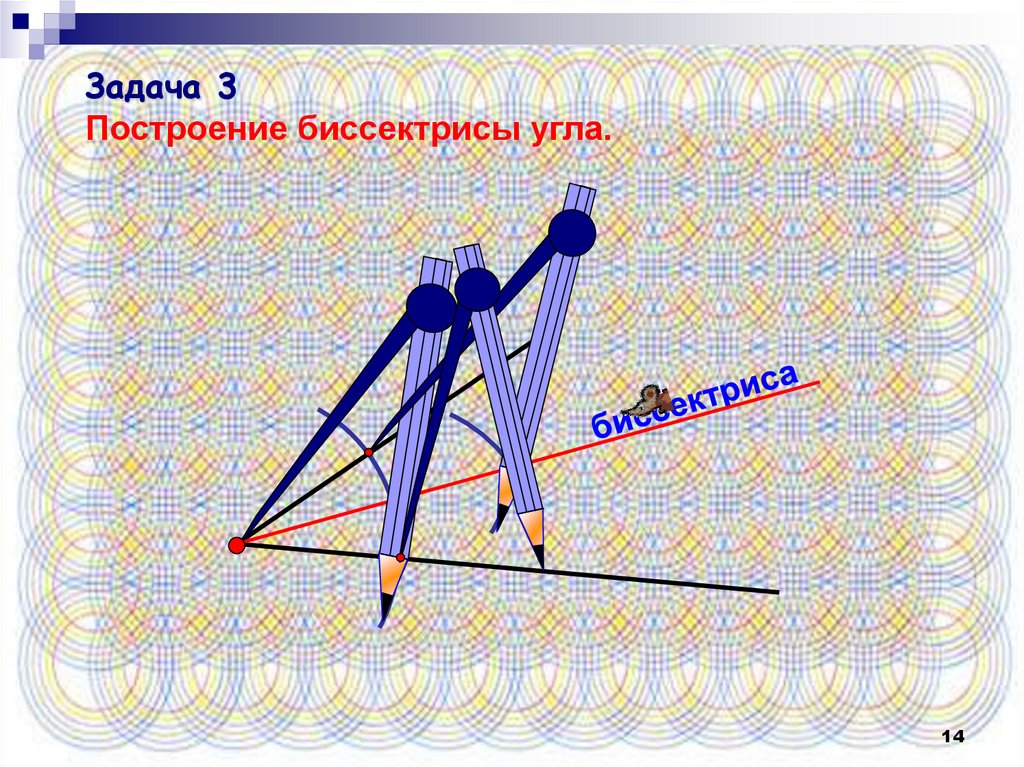
14.

Задача 3
Построение биссектрисы угла.
14

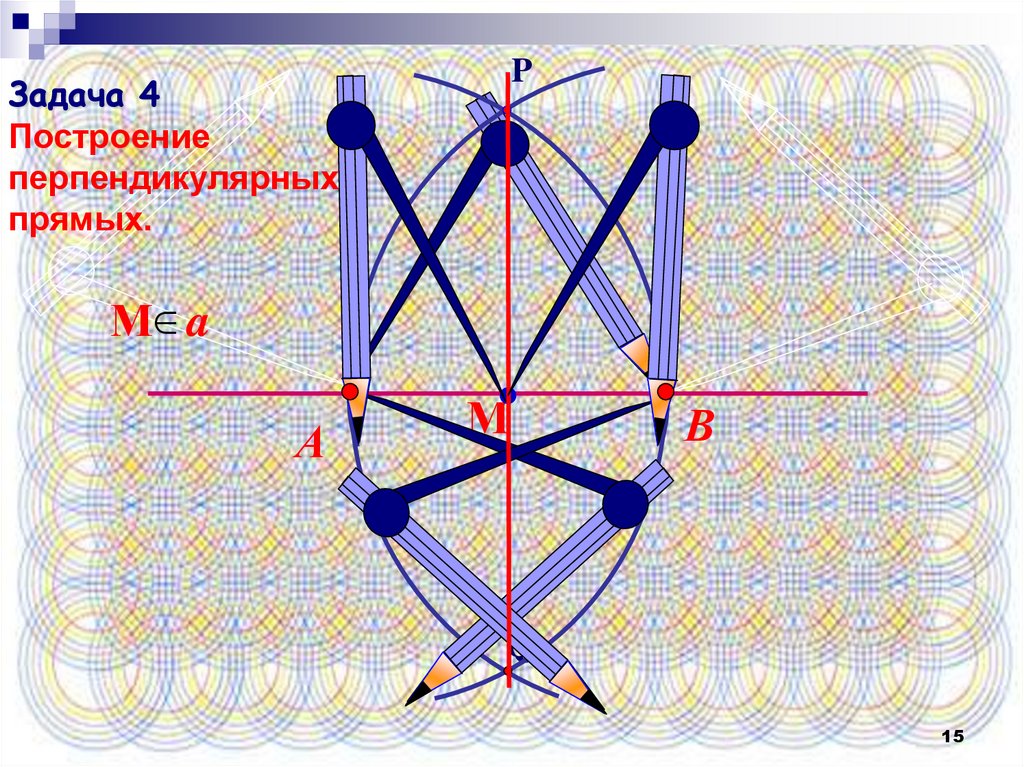
15.

P
Задача 4
Построение
перпендикулярных
прямых.
М a
А
М
В
Q
15

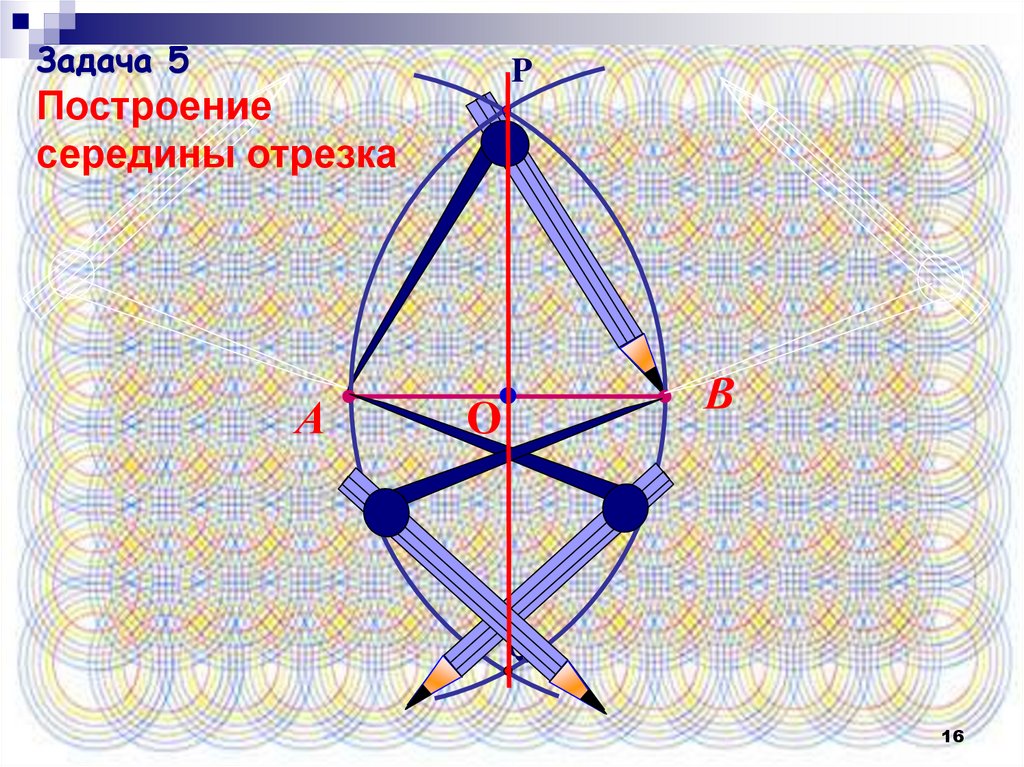
16.

Задача 5
P
Построение
середины отрезка
А
В
О
Q
16