Смесительный бак с регулированием уровня и температуры. Пример

1. Пример. Смесительный бак с регулированием уровня и температуры. АС - площадь поперечного сечения бака. F(h) = kh1/2 Горячий

Пример. Смесительный бак с регулированием уровня и
температуры.
АС - площадь поперечного сечения бака.
F(h) = kh1/2
Температура
Fx,Tx
Td,Fd
возмущающее
действие
Fг,Tг
Регулятор
уровня
F(h),T
Горячий входной поток характеризуется температурой Тг и
регулируемым расходом Fг, холодный поток – температурой Тх и
регулируемым расходом Fх. Возмущение - Td,Fd. . В баке происходит
полное перемешивание, выход зависит от высоты жидкости.

2. 1. Уравнения материального и энергетического балансов. АС(dh/dt)= Fг + Fx + Fd - F(h) ρCpAC[d(hT)/dt]=ρCp[FгTг + FxTx + FdTd -

F(h)T] (1)
Количество тепла=масса*уд.теплоемкость*разность температур.Но все
нужно считать во времени. Теплоемкость-кол-во тепла, которое нужно подвести к
системе, чтобы поднять температуру на 1 градус.
2. Линеаризация. S – индекс рабочей точки.
f (a )
f (a )
f ( x) f (a)
( x a)
( x a ) 2 ...
1!
2!
1
F (h) F (hS ) k (h hS ) / hS1/ 2 :
2
1
F (h)T F (hS )TS F (hS )(T TS ) TS k (h hS ) / hS1/ 2 ...
2
hT hS TS hS (T TS ) TS (h hS )
Fd Td Td S Fd S Fd S (Td Td S ) Td S ( Fd Fd S )
(2)

3. 3. Запишем для установившегося режима исходные уравнения. 0= FГs + FXs + Fds - F(hS) 0=FГsTГs +FXsTXs+FdsTds - F(hs)TS] (3) 4.

Запишем уравнения в отклонениях.
Для этого из уравнения (1) вычтем уравнение (3)
АС(dh/dt)= Fг + Fx + Fd - F(hs) –(1/2k(h-hs))/hs1/2
- 0= FГs + FXs + Fds - F(hS)
АС(dh/dt)= (Fг –FГs) + (Fx – FXs) + (Fd –Fds) –(1/2k(h-hs))/hs1/2

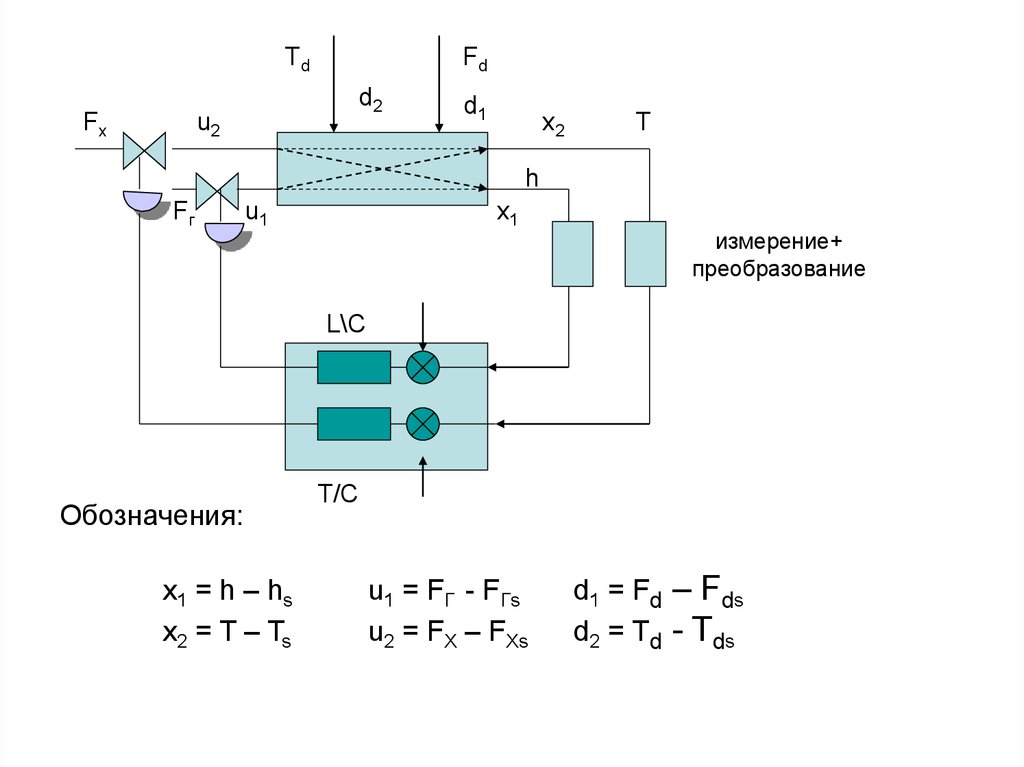
4. Обозначения: x1 = h – hs u1 = FГ - FГs d1 = Fd – Fds x2 = T – Ts u2 = FX – FXs d2 = Td - Tds

Td
Fx
Fd
d2
u2
d1
x2
T
h
Fг
u1
x1
измерение+
преобразование
L\C
Обозначения:
x1 = h – hs
x2 = T – Ts
T/C
u1 = FГ - FГs
u2 = FX – FXs
d1 = Fd – Fds
d2 = Td - Tds

5.

dx1
1
1
[u1 u2 d1 kx1 / hs1/ 2 ], т.к.
dt
AC
2
F (hs ) khs1/ 2
1
1 F (hs )
dx1
dt A [u1 u2 d1 2 h x1 ]
C
s
dx2 ( 1 )[(T T )u (T T )u (T T )d F d F (h ) x ]
S
1
X
S
2
dS
S
1
dS 2
S
2
dt
AC hs
u1
x1
d1
x u d
x2
d 2
u2
1
1 F (hs )
1
0
2 A h
A
A
C s
C
B C
A
F
(
h
)
T
T
T
T
s
X
S
S
0
AC hs
AC hS
AC hs
y1
x1
y x
y2
x2
1 0
C
0
1

6. 4. Найдем решение. т.к. матрица А – диагональна, то она уже как бы приведена к каноническому виду. Решаем ΔА = |А – λI |=0,

4. Найдем решение.
t
x(t ) e A(t t0 ) x0 e A(t r ) [ Bu (r ) Td (r )]dr
t0
т.к. матрица А – диагональна, то она уже как бы приведена к каноническому
виду. Решаем ΔА = |А – λI |=0, т.е. известно
1 F (hs )
1
2 AC hs
1t
e
e
0
At
F (hs )
2
;
AC hs
12 FA( hhS )
0 e C S
2 t
e
0
0
F ( hS )
AC hS
e
Рассчитаем реакцию на единичное ступенчатое возмущение по u1, u2 в t=0
при условии
x10
x(0) x0 , a d1 d 2 0
x20
Для этого случая
t
x(t ) e x0 e
At
0
A( t r )
e x10 e
1t
x1
Bu (r )dr; x(t )
x2
t
1 ( t r )
0
t
e 2t x20 e 2 (t r )
0
2
dr
AC
T TX 2TS
dr
AC hs