Similar presentations:
Решение квадратных уравнений с параметрами. Метод плавающей параболы
1. Решение квадратных уравнений с параметрами. Метод плавающей параболы
2.
Параметр в уравнении или неравенственекоторая плавающая величина, т.е.
число, принимающая различные значения
Уравнение с параметрами —
математическое уравнение внешний вид и
решение которого зависит от значений
одного или нескольких параметров.
Решить уравнение с параметром означает,
что нужно найти все системы значений
параметров, при которых выполняется то
или иное требование.
3.
При каких условиях корниуравнения
ax bx c 0
2
меньше числа М?
x x M
1
2
4.
Рассмотрим соответствующуюквадратичную функцию
y ax bx c
2
Найдем вершину параболы
b
x0
2a
y0 y( x0 )
5.
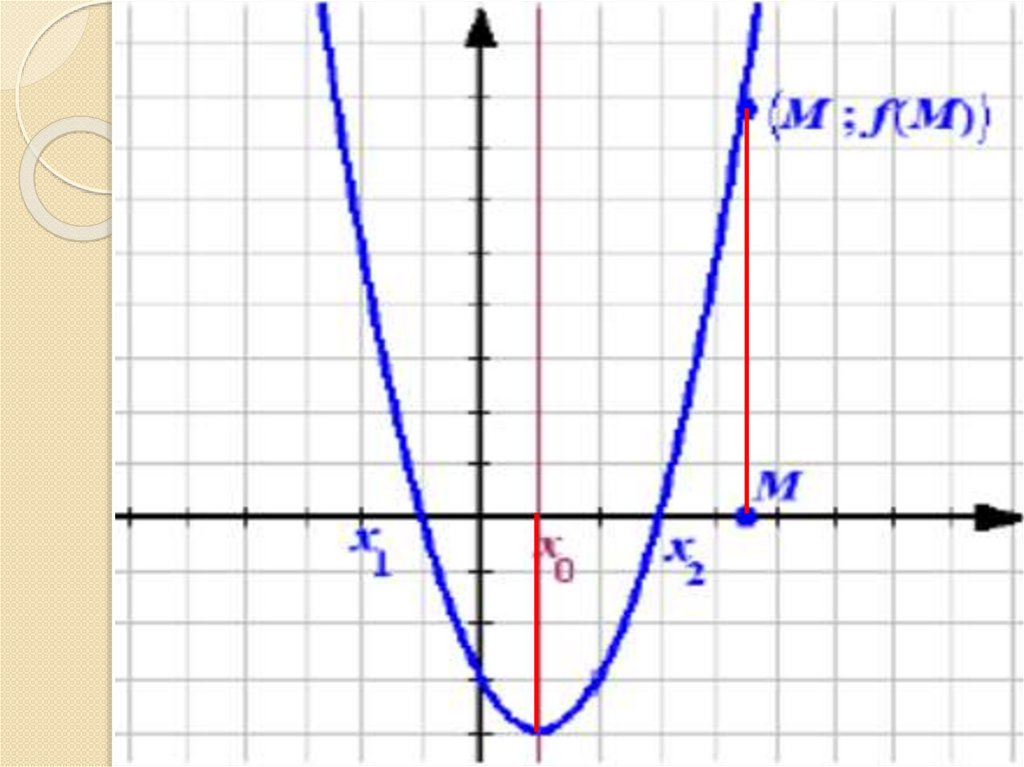
I случайa 0
Ветви параболы направлены вверх
6.
Условие существованиядействительных корней квадратного
уравнения
D 0
7.
8.
a 0D 0
x
M
0
f
(
M
)
0
9.
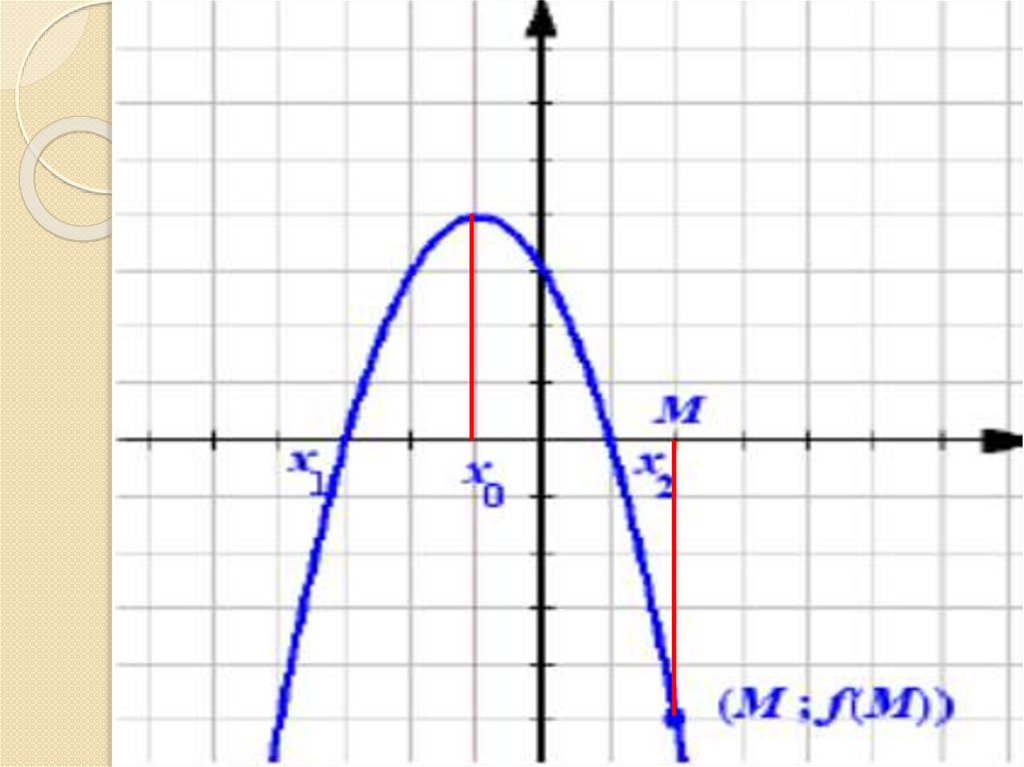
II случайa 0
Ветви параболы направлены вниз
10.
11.
a 0D 0
x
M
0
f ( M ) 0
12.
13.
При каких значениях параметра mкорни уравнения
x 2(m 1) x 4m 7 0
2
отрицательны.
14.
y x 2(m 1) x 4m 72
D 4( m 1) 4( 4m 7)
2
4m 8m 4 16m 28
2
4m 24m 32
2
2(m 1)
x0
(m 1)
2
f (0) 4m 7
15.
4m 24m 32 0(m 1) 0
4m 7 0
2
16.
( ;2] [4; )(1; )
7
( ; )
4
7
m ( ;2] [4; )
4
17.
При каких значениях параметра р корни уравнения1 группа
x 2 2( p 1) x 9 p 5 0
меньше 0.
2 группа
x 2 (3 p 1) x (2 p 2 4 p 6) 0
меньше -1
3 группа
меньше 1
x 2 (2 p 1) x ( p 2 p 2) 0
18.
1 группа5
p ( ;1) (6; )
9
2 группа
( ;4)
3 группа
( ; 1)
19.
При каких условиях корни уравненияax bx c 0
2
больше числа М?
M x1 x2
20.
a 0D 0
x
M
0
f ( M ) 0
или
a 0
D 0
M
x
0
f ( M ) 0






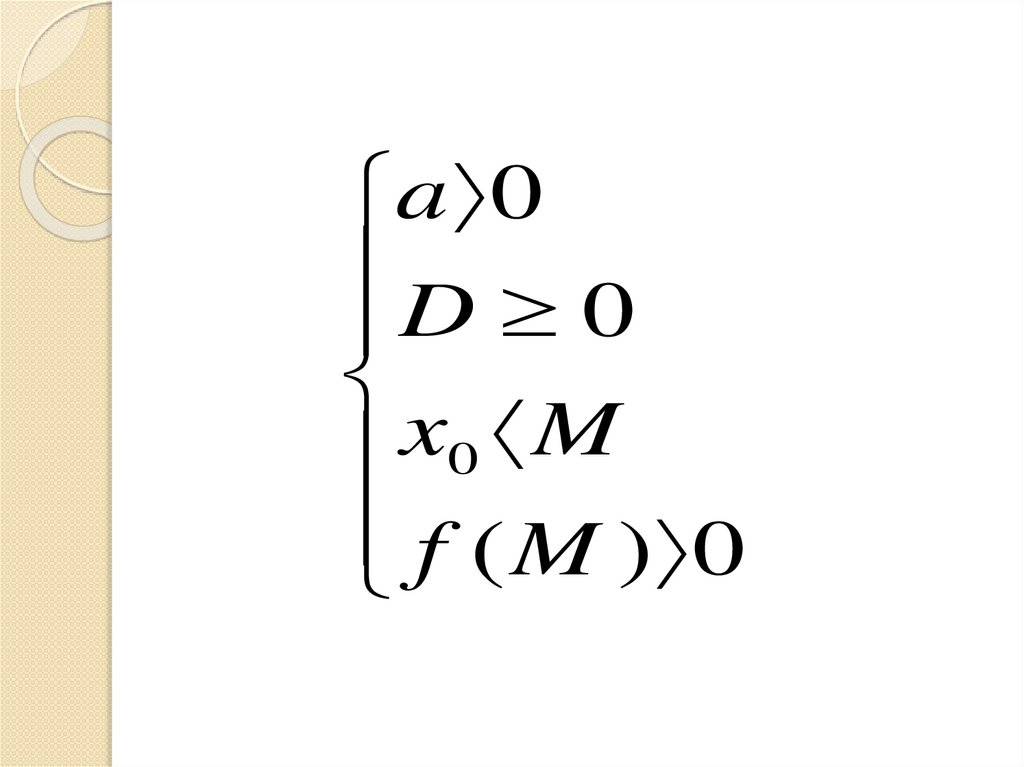

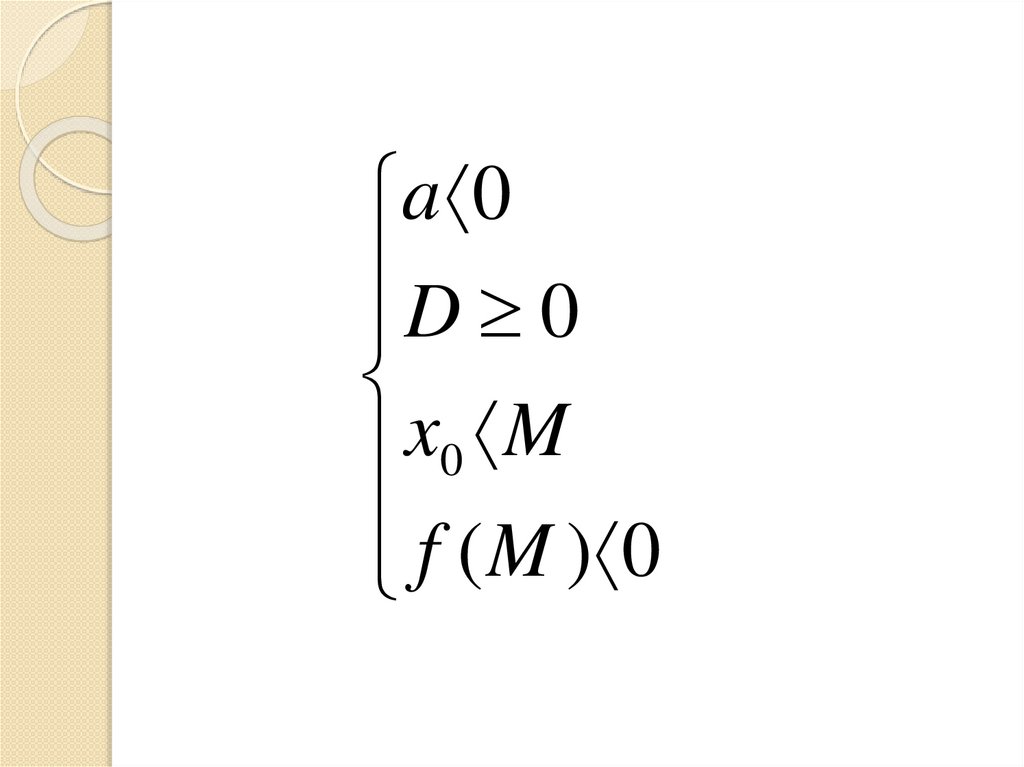

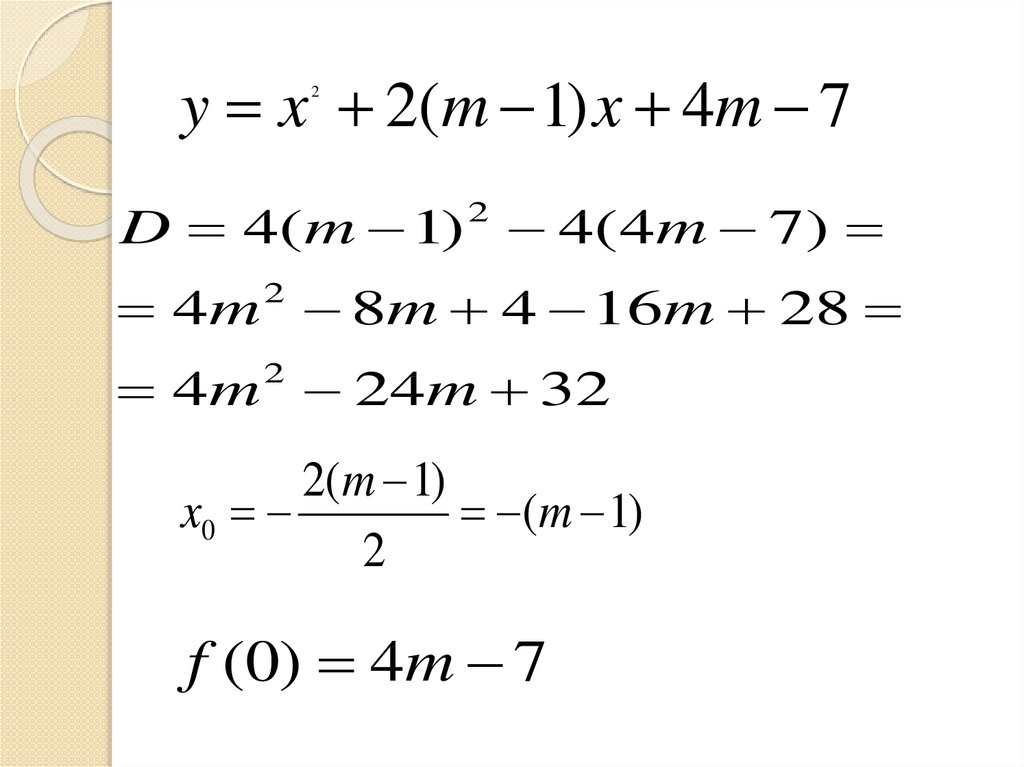
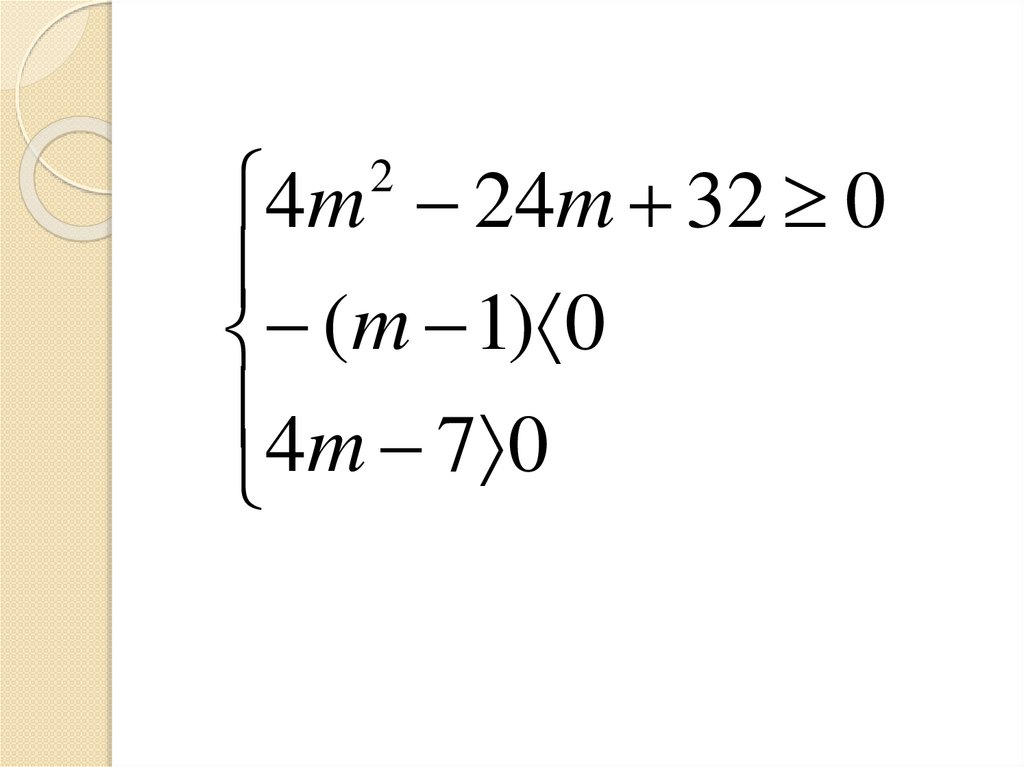




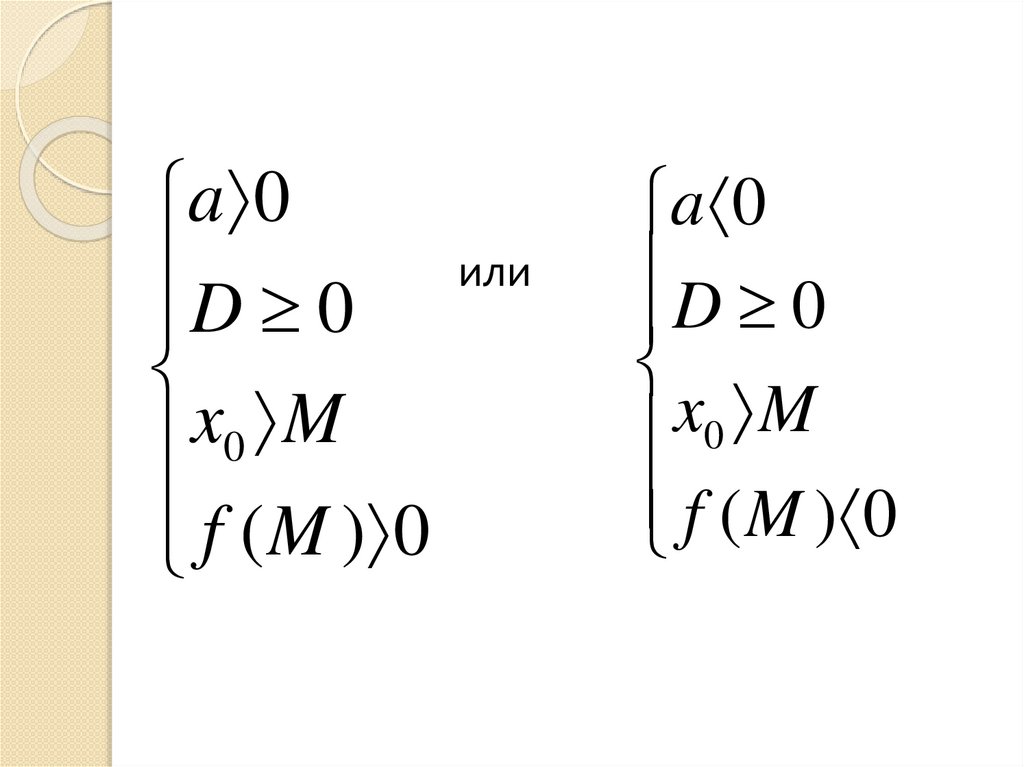
 mathematics
mathematics








