Similar presentations:
Кинематический анализ плоского механизма. (Задача к-11)
1. Расчетно-графическая работа №1
Задача К-11. Кинематический анализплоского механизма
Рисунок 3, вариант 11
2. Оформление.
Чувашский государственный университетим. И.Н.Ульянова
Факультет энергетики и электротехники
Кафедра высшей математики и теоретической
механики им. С.Ф.Сайкина
3.
Расчетно-графическая работа №1по теме:
«Кинематический анализ
плоских механизмов»
Рис. 3, вариант 11
4.
Выполнил:студент группы ФЭиЭТ-…-15
Фамилия И.О.
Проверила:
Васильева Е.В.
Чебоксары - 2016
5. Дано:
AB 80 смr 20 см
R 30 см
s ОA f (t ) 10t 2 50t , см
s1 60, см
45 0
00
6. Найти:
1. Скорости точек A, B, C, D.2. Угловые скорости стержня АВ и колеса в
заданном положении.
3. Ускорение точки А.
7. Заданный рисунок
AО
D
C
B
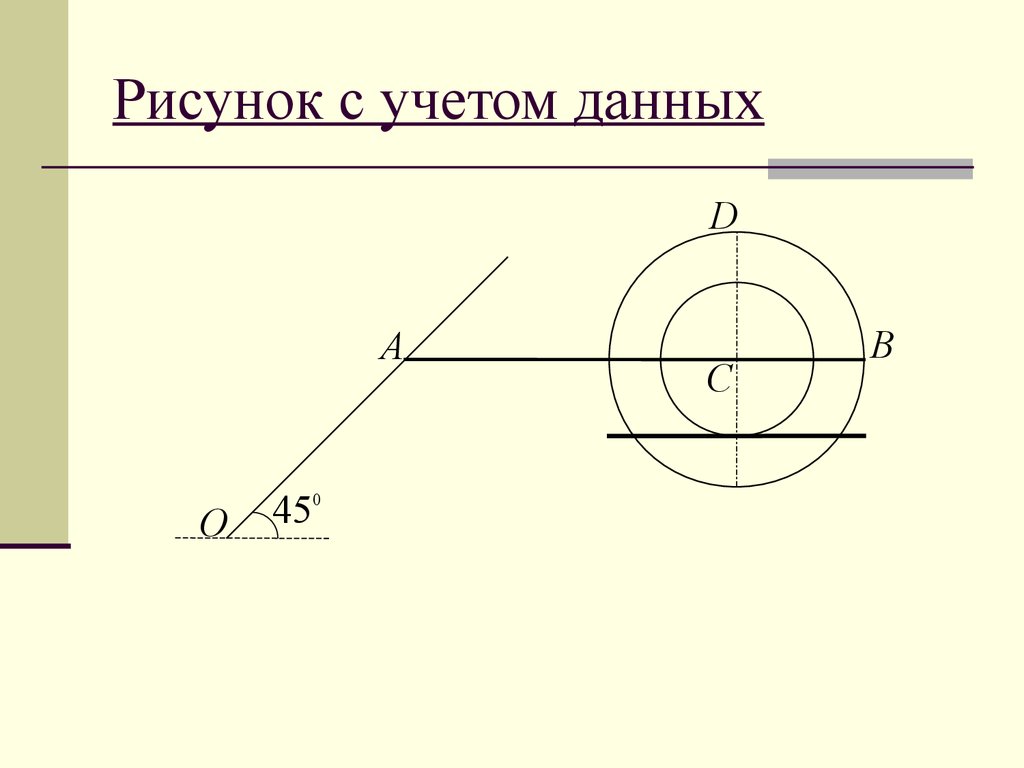
8. Рисунок с учетом данных
DA
О
450
C
B
9. Решение:
1. Рассмотрим движение точки А.По условию задачи т.А движется по прямой
ОА по закону s OA f (t ) , положение т.А
соответствует положительному
направлению движения.
Тогда движение точки А задано
естественным способом.
10.
Для того чтобы определить скорость иускорение т.А, найдем время t1 , когда
расстояние, пройденное точкой станет s1.
Для этого решим уравнение:
s1 f (t ) 60 10t 50t
2
11.
Получим: t1 1 .Определим скорость и ускорение:
ds
vA s 50 20t
dt
dv A
wA
v A 20
dt
2
v
wAn A
12.
При t1 1 с получим:v A 50 20 1 70 см / с 0 , т.е. направление
вектора скорости т.А совпадает с
положительным направлением движения.
w A 20 см / с 2 0 , т.е. направление вектора
касательного ускорения т.А совпадает с
положительным направлением движения.
13.
vA 70wA
0
2
2
n
Тогда полное ускорение:
2
n2
wA wA wA 202 02 20 см / с 2 , совпадает
по направлению и по длине с вектором
касательного ускорения т.А.
Изобразим все вектора на рисунке.
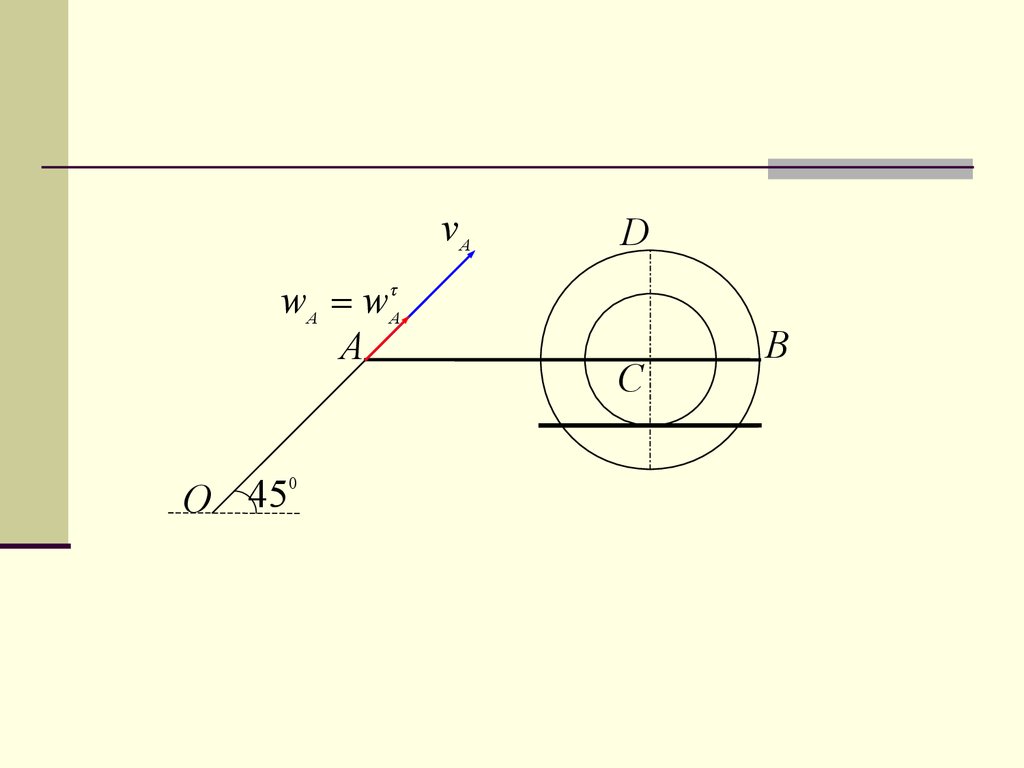
14.
vAwA wA
A
О 45
0
D
C
B
15.
2. Рассмотрим движение стержня АВ.Стержень совершает ППД. Тогда для
определения скоростей его точек
определим мцс – т. PAB (на пересечении
перпендикуляров к скоростям точек).
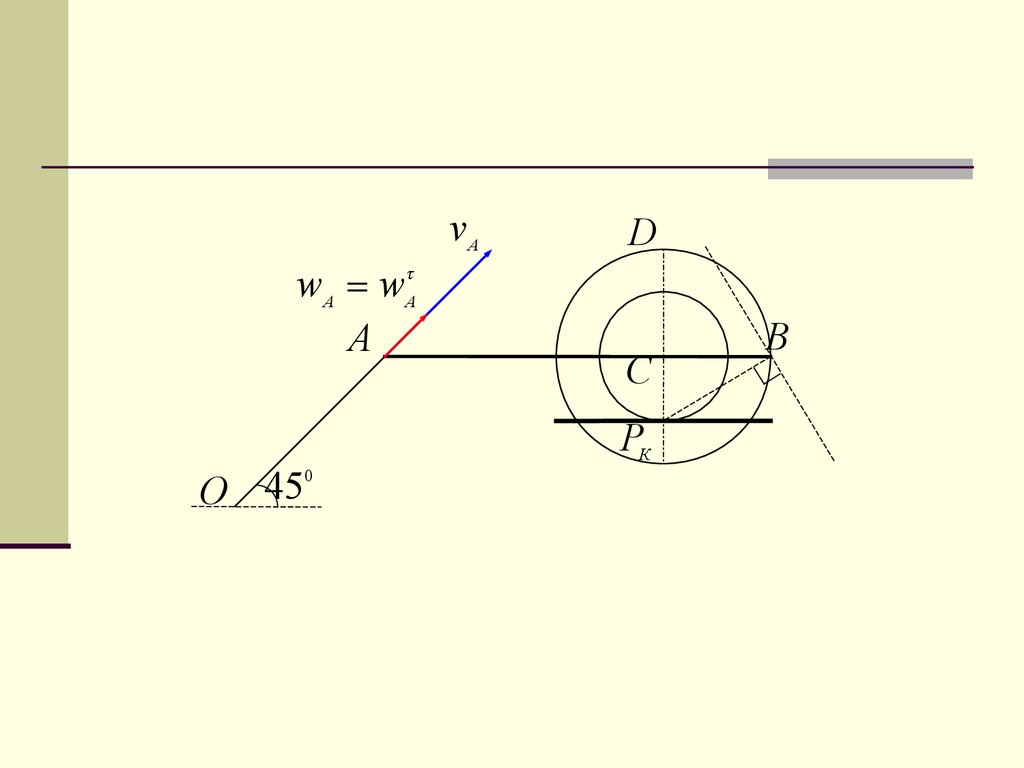
16.
3. Рассмотрим движение колеса.Оно совершает ППД. Положение мцс колеса
известно – т. PК.
Тогда можем определить положение прямой,
на которой находится вектор скорости т.В.
17.
wA wAA
0
45
О
vA
D
C
PК
B
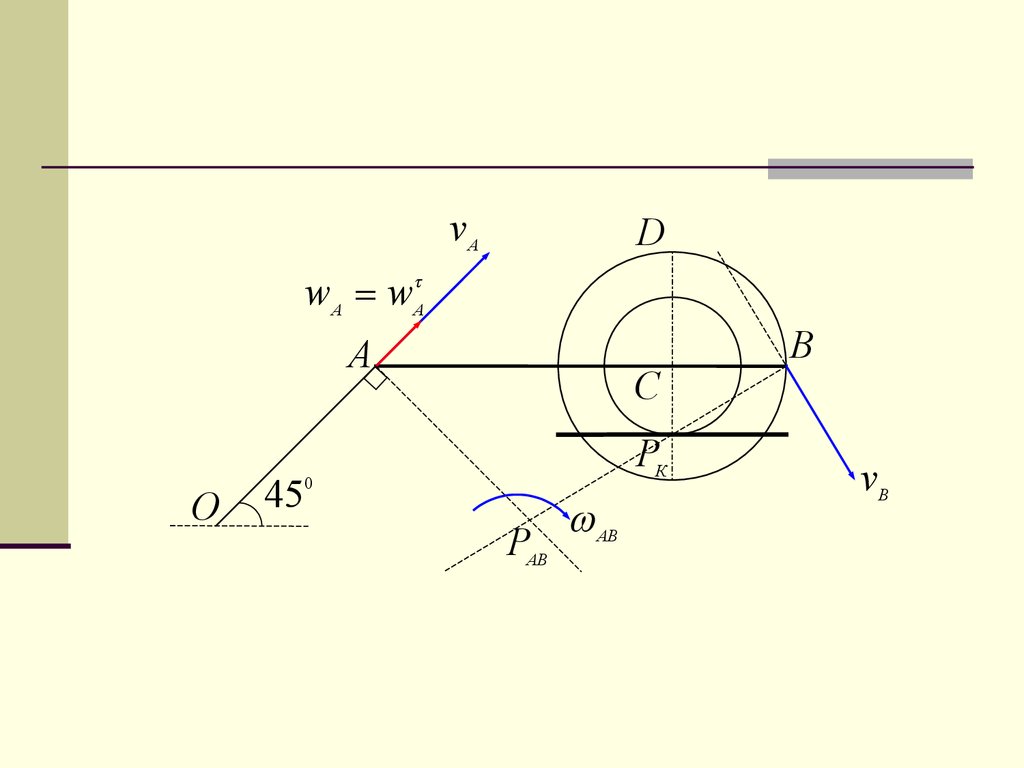
18.
Возвращаемся к пункту 2.Т.к. известно положение прямой, на которой
находится вектор скорости т.В, то можем
определить мцс стержня АВ и направление
вращения угловой скорости этого стержня.
Тогда по направлению угловой скорости
можем окончательно определить на
рисунке направление вектора скорости т.В.
19.
wA wAvA
D
A
О
45
C
PК
0
PAB
AB
B
vВ
20.
Определим угловую скорость стержня искорость точки В из соотношения:
vA
vB
AB
, где расстояния APAB и BPAB
APAB BPAB
определим по теореме синусов из
треугольника АBPAB .
r
20
0
A 45 , В arctg arctg 33,690 ,
R
30
PAB 1800 A B 101,310
21.
Тогда по теореме синусов:APAB
BPAB
AB
0
0
0
sin 101,31 sin 33,69 sin 45
АВ
80
APAB
sin 33,69
0,555 45,26 см
sin 101,31
0,981
АВ
80
BPAB
sin 45
0,707 57,656 см
sin 101,31
0,981
22.
Тогда:vA
70
1
AB
1,547 с
APAB 45,26
vB АВ ВРАВ 1,547 57,656 89,182 см / c
23.
Переходим к 3 пункту.Зная направление скорости т.В, можем
определить угловую скорость колеса,
направления скоростей точек С и D.
24.
wA wAvA
D
A
О
45
vD
C
PК
0
PAB
AB
vС B
К
vВ
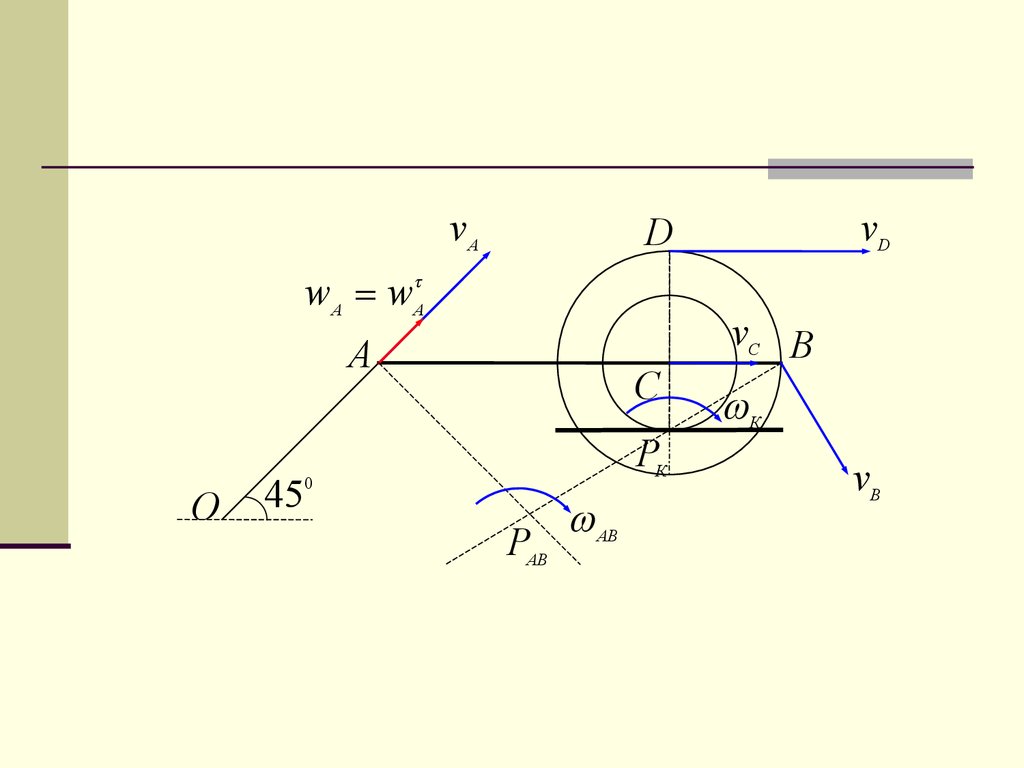
25.
Угловую скорость колеса и скорости точек Си D определим из соотношения:
vB
vС
vD , где расстояния BP , СP
К
К
К
BPК CPК DPК
и DPК легко найти по рисунку.
BPК R 2 r 2 302 202 36,056 см
CPК r 20 см
DPК R r 30 20 50 см
26.
Итак:vB
89,182
К
2,474 с 1
BPК 36,056
vС К СРК 2,474 20 49,469 см / c
vD К DРК 2,474 50 123,673 см / c





















 mechanics
mechanics








