Решение уравнений

1.

2.

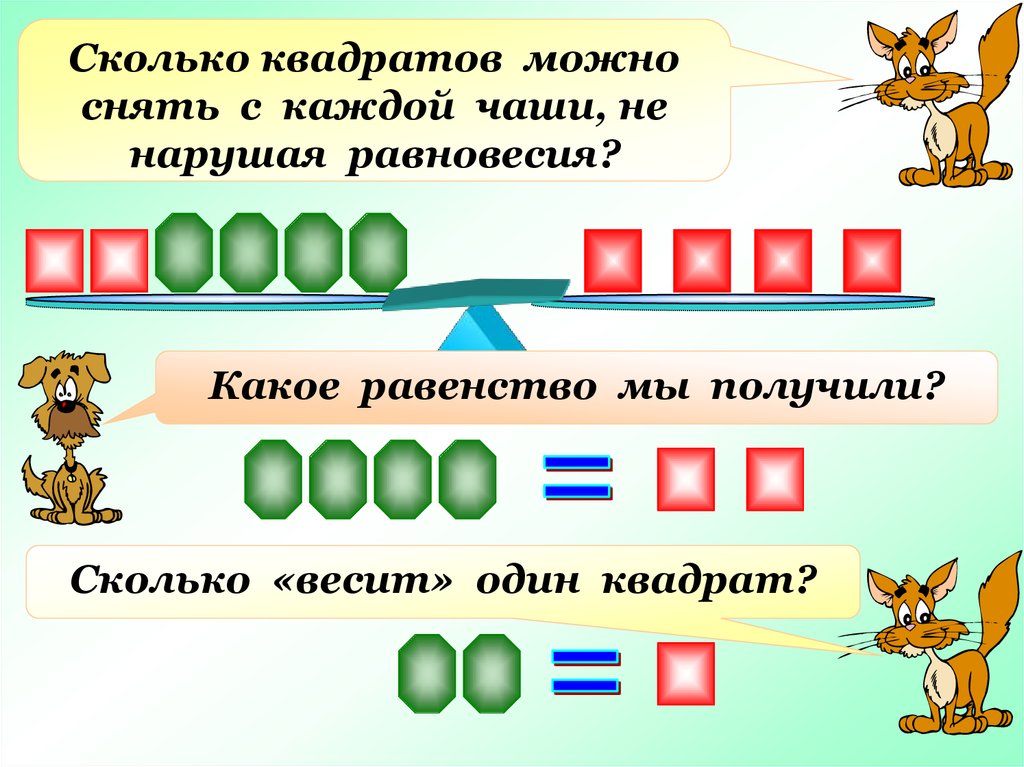
Сколько квадратов можно
снять с каждой чаши, не
нарушая равновесия?
Какое равенство мы получили?
Сколько «весит» один квадрат?

3.

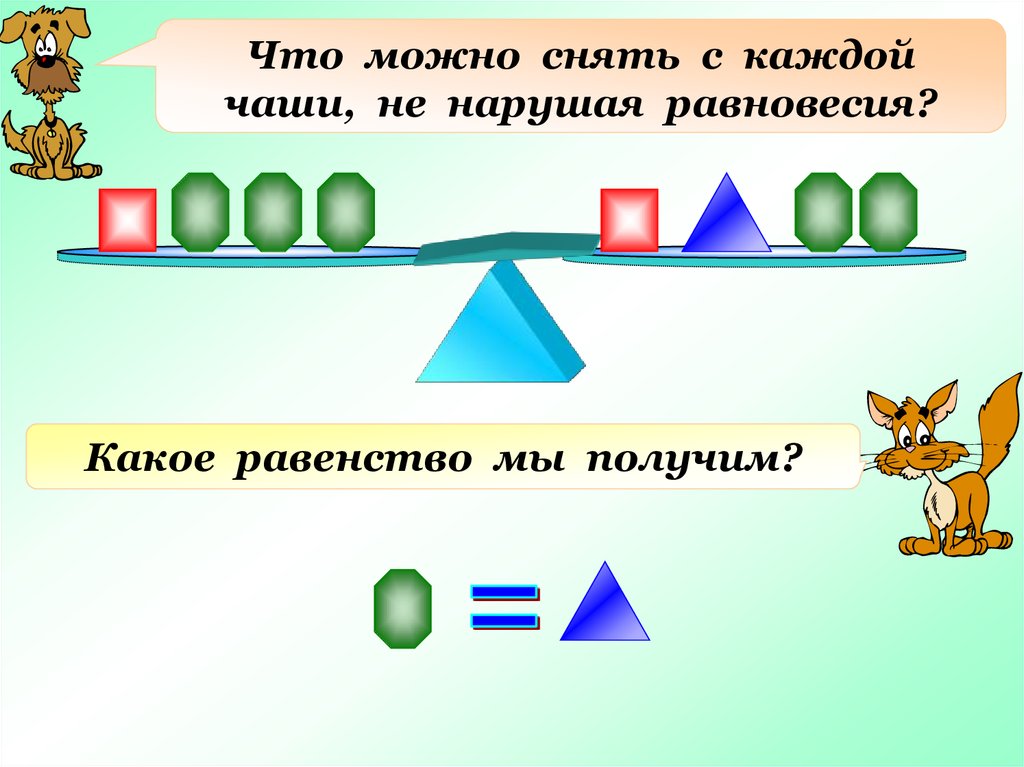
Что можно снять с каждой
чаши, не нарушая равновесия?
Какое равенство мы получим?

4.

Что можно снять с каждой
чаши, не нарушая равновесия?
х кг х кг х кг х кг
х кг
х кг
х кг
Запишите, какое уравнение
было первоначально и какое
получилось?
5кг 1кг

5.

х кг х кг х кг х кг
х кг
х кг
х кг
5кг 1кг
Перенесем 2х из правой части
в левую с противоположным
знаком.
х кг х кг х кг х кг
х кг
х кг
х кг
5кг 1кг

6.

Решить самостоятельно:

7.

Решить уравнение:
Решение:
+
+

8.

Решить задачу по картинке:
80г
Сколько весит груша?

9.

Найдите и исправьте ошибки
в решении уравнения:
+

10.

Рассмотрим способы решения
уравнений.
Перенос членов уравнения
из одной части в другую.

11.

Решите самостоятельно:

12.

С помощью умножения обеих
частей уравнения на одно и
то же число можно
освободиться от дробных
чисел.

13.

Можно обе части уравнения
разделить на одно и то же
число.

14.

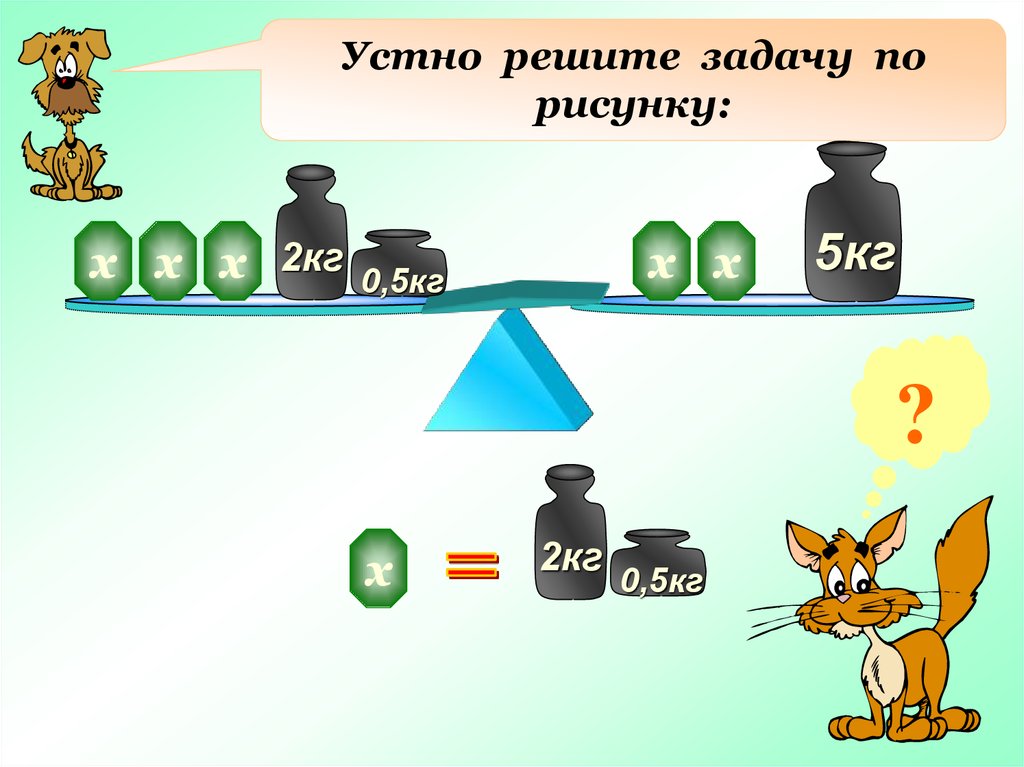
Устно решите задачу по
рисунку:
х х х 2кг
х х
0,5кг
5кг
?
х
2кг
0,5кг

15.

Можно решать уравнение,
используя основное свойство
пропорции.
х 3 7
6
3

16.

В трех чашах я хранил жемчуг. Подарил я
старшему сыну половину жемчужин из
первой чаши, среднему – треть из второй,
младшему – только четверть жемчужин из
третьей чаши. Затем подарил старшей
дочери четыре лучших жемчужин из 1 чаши,
средней – 6 жемчужин из 2 чаши,
а третьей – только две
жемчужины из 3 чаши.
В первой чаши осталось 36 жемчужин,
во второй – 12, а в третьей – 19
жемчужин.
Сколько жемчужин хранилось
в каждой чаше?
Печать

17.

Осталось:
1
2
Сколько жемчужин
я хранил в каждой
чаше?
?
1
3
?
1
4
?