Similar presentations:
Производная и ее применение
1. Производная и ее применение Занятие №1
12. Определение
Производной функции в данной точкеназывается предел отношения приращения
функции к приращению аргумента при
условии ,что приращение аргумента
стремится к нулю
2
3. Производные основных элементарных функций
=(
4. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
5. НАЙДИТЕ ПРОИЗВОДНУЮ
1)3 4 3
f ( x) x 2 x x 5
4
3
2
f ( x) 1 3ответ
x 6x 1
2 ответ
2)
3)
1
f ( x) 310
e
ответ
х
f ( x) 10e ln 4 x
x
x
f ( x) sin 5 x
f ( x)
5 sin 10 x
4 ответ
2
4)
5)
f ( x) 2 10 х 12 х
x
f ( x) 2
3
x
2
5
ответ
In2 30 x 12
6.
1) f ( x) 3x 5 x 2 x 4 x 67
5
3
Решение
7
5
3
f (x) 3 (x ) 5 (x ) 2 ( x ) 4 ( x) 6
3 7x 5 5x 2 3x 4 1 0
f (x)
6
4
2
f ( x) 21x 25 x 6 x 4
6
4
2
7.
2) f ( x) (5 sin x x )6
Решение
f ( x) (5 sin x x )
6
5(sin x) ( x )
6
5 cos x 6 x
5
8.
3) f ( x) 12 x tg ( x)Решение
f (x) 12 (x ) - (tg(x))
1
f (x) 12 1 2
cos x
1
f (x) 12 2
cos x
9.
f(x) x sin x4
Решение
4
4
f (x) (x ) sinx x (sin x)
f (x) 4x sin x x cos x
3
4
10.
2x5) f ( x)
4x 3
Решение
(2x) (4x 3) - 2x (4x 3)
f (x)
(4x 3)2
2(4x 3) - 2x 4 8 x 6 8 x
6
f (x)
2
2
(4x 3)
(4 x 3)
(4 x 3) 2
11.
f(g(x)) f (x) g (x)Пример
f ( x) ( 5 x 11)
4
Решение
4
f (x) ((-5x 11) ) (5x 11)
f(x) 4 (-5x 11) ( 5) 20 ( 5x 11)
3
3
12.
f(x) cos 5 xРешение
f (x) (cos5x) (5x) -sin5x 5
f (x) -5sin5x
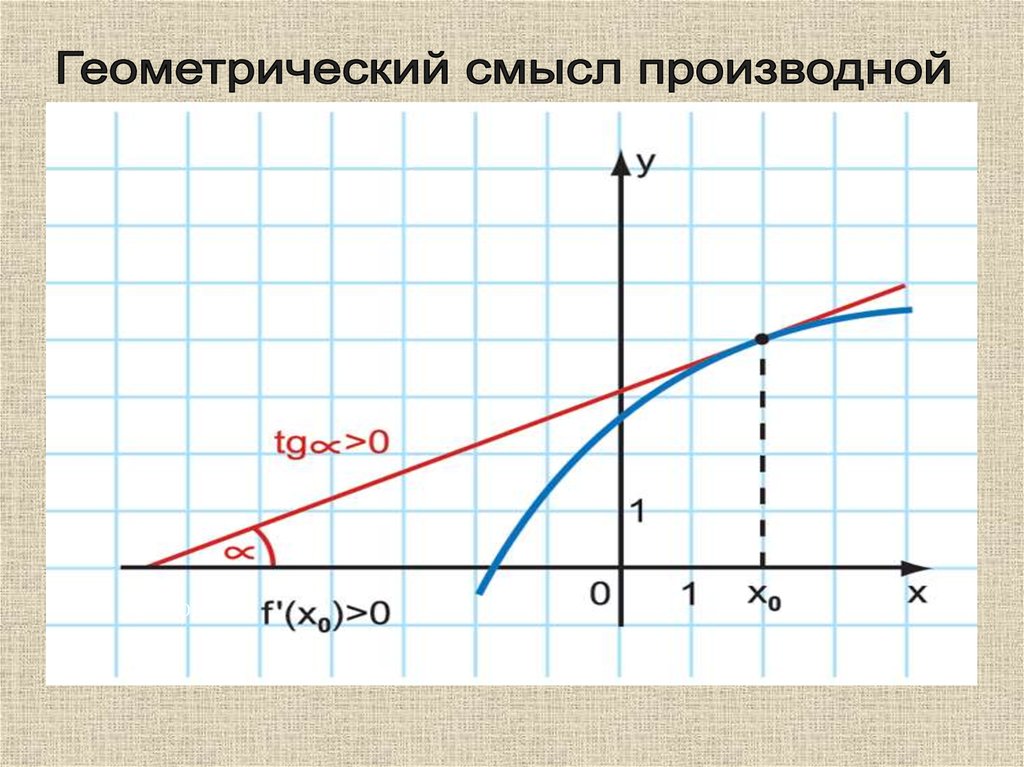
13. Геометрический смысл производной
состоит втом, что значение производной функции y = f (x)
в точке x равно угловому коэффициенту
касательной к графику функции в точке с
абсциссой x.
13
14.
ααααα′15.
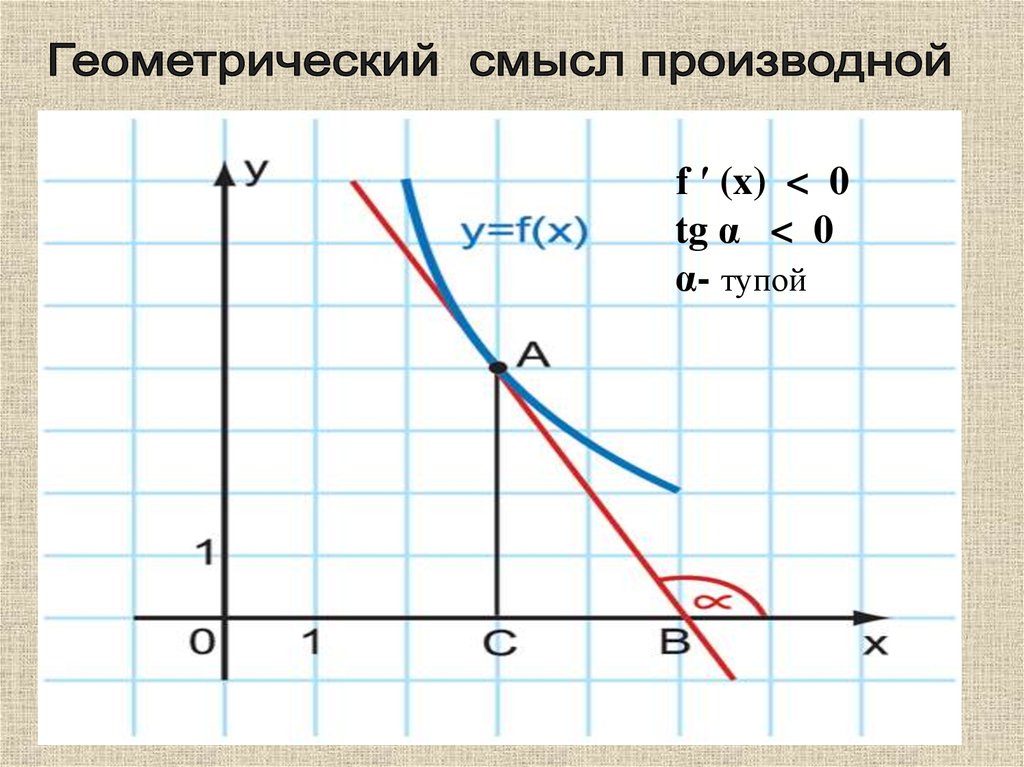
f ′ (x) < 0tg α < 0
α- тупой
16.
Геометрический смысл производной17.
18.
19. 12. На рисунке изображен график функции y=f(x) и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной
20.
S (t ) v(t )v (t ) a(t )
21.
ПримерМатериальная точка движется по прямой
так, что ее скорость в момент времени t равна
v(t ) t 3 2t.
Найдите ускорение точки
времени t = 3.
Решение
a (t ) v (t )
v (t ) (t 2t ) 3 * t 2
3
2
v (3) 3 * 3 2 25
2
Ответ:
a (3) 25
в
момент



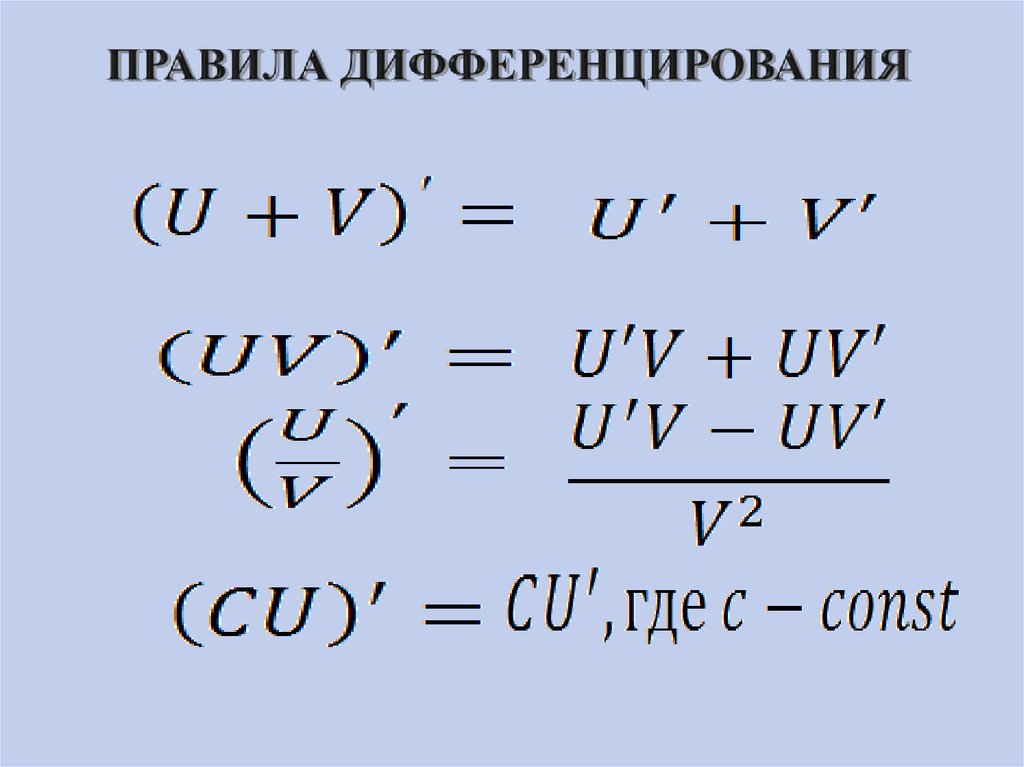















 mathematics
mathematics








