Прямоугольник. Свойства прямоугольника

1. Тема урока: Прямоугольник

ТЕМА УРОКА: ПРЯМОУГОЛЬНИК

2. Выбрать геометрические фигуры, которые являются многоугольниками

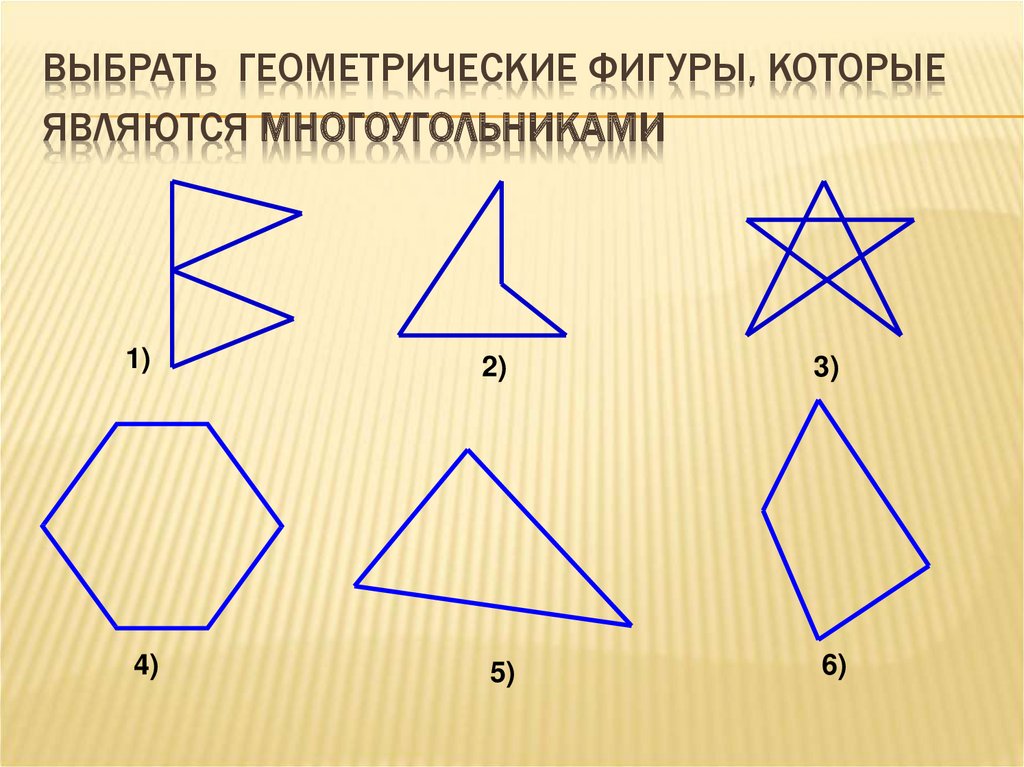
ВЫБРАТЬ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ, КОТОРЫЕ
ЯВЛЯЮТСЯ МНОГОУГОЛЬНИКАМИ
1)
2)
3)
4)
5)
6)

3. Среди выбранных многоугольников назовите те, которые являются выпуклыми многоугольниками

СРЕДИ ВЫБРАННЫХ МНОГОУГОЛЬНИКОВ НАЗОВИТЕ ТЕ,
КОТОРЫЕ ЯВЛЯЮТСЯ ВЫПУКЛЫМИ
МНОГОУГОЛЬНИКАМИ
1)
2)
3)
4)
5)
6)

4. АВ || CD и АD || СВ

АВ || CD И АD || СВ
АВСD – параллелограмм

5. АВ || CD и АD || СВ

АВ || CD И АD || СВ
АВСD – параллелограмм

6. АВСD – параллелограмм

АВСD – ПАРАЛЛЕЛОГРАММ
1 свойство:
АВ = CD
АD = СВ
‫ ‬A = ‫ ‬С
‫ ‬В = ‫ ‬D

7. АВСD – параллелограмм

АВСD – ПАРАЛЛЕЛОГРАММ
‫ ‬A = ‫ ‬С
1 свойство:
‫ ‬В = ‫ ‬D
АВ = CD
АD = СВ

8. АВСD – параллелограмм

АВСD – ПАРАЛЛЕЛОГРАММ
2 свойство:
АС и ВD пересекаются и
АО = ОС, ВО = ОD

9. АВСD – параллелограмм

АВСD – ПАРАЛЛЕЛОГРАММ
2 свойство:
АС и ВD пересекаются и
АО = ОС, ВО = ОD

10. Четырёхугольник АВСD – параллелограмм, если

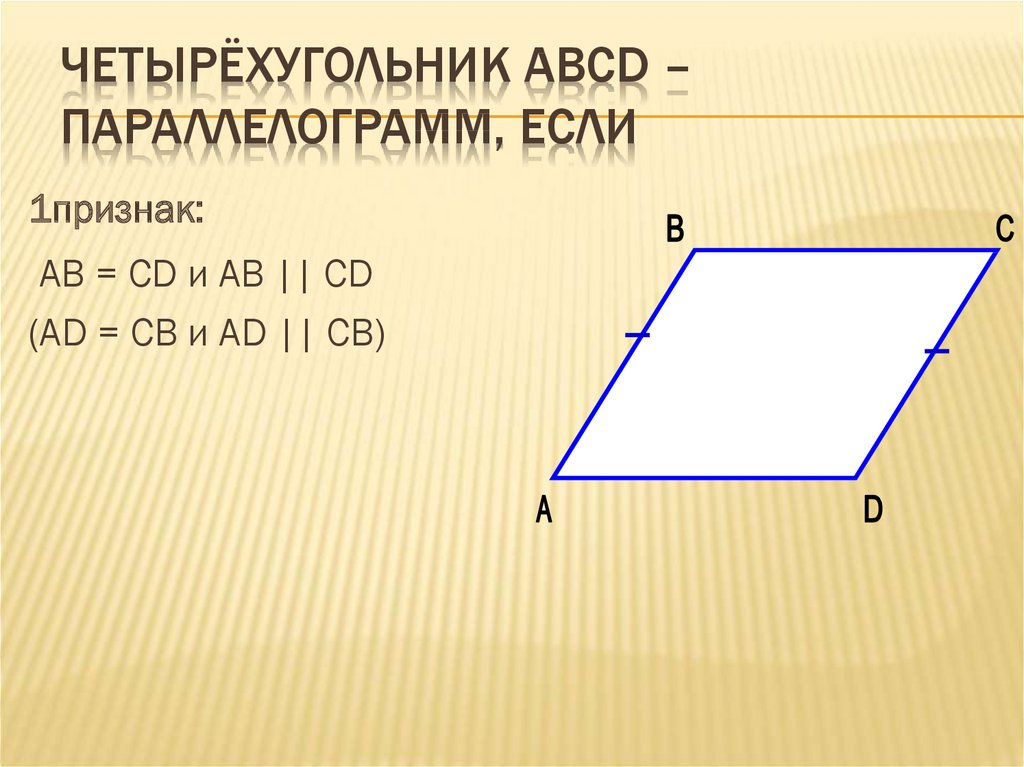
ЧЕТЫРЁХУГОЛЬНИК АВСD –
ПАРАЛЛЕЛОГРАММ, ЕСЛИ
1признак:
АВ = CD и АВ || CD
(АD = СВ и АD || СВ)

11. Четырёхугольник АВСD – параллелограмм, если

ЧЕТЫРЁХУГОЛЬНИК АВСD –
ПАРАЛЛЕЛОГРАММ, ЕСЛИ
1признак:
АВ = CD и АВ || CD
(АD = СВ и АD || СВ)

12. Четырёхугольник АВСD – параллелограмм, если

ЧЕТЫРЁХУГОЛЬНИК АВСD –
ПАРАЛЛЕЛОГРАММ, ЕСЛИ
2 признак:
АВ = CD
АD = СВ

13. Четырёхугольник АВСD – параллелограмм, если

ЧЕТЫРЁХУГОЛЬНИК АВСD –
ПАРАЛЛЕЛОГРАММ, ЕСЛИ
2 признак:
АВ = CD
АD = СВ

14. Четырёхугольник АВСD – параллелограмм, если

ЧЕТЫРЁХУГОЛЬНИК АВСD –
ПАРАЛЛЕЛОГРАММ, ЕСЛИ
3 признак:
АС и ВD пересекаются
и АО = ОС, ВО = ОD

15. Четырёхугольник АВСD – параллелограмм, если

ЧЕТЫРЁХУГОЛЬНИК АВСD –
ПАРАЛЛЕЛОГРАММ, ЕСЛИ
3 признак:
АС и ВD пересекаются
и АО = ОС, ВО = ОD

16. АВСD – параллелограмм. Найти угол В.

АВСD – ПАРАЛЛЕЛОГРАММ. НАЙТИ УГОЛ В.

17. АВСD – параллелограмм. Найти углы С и D.

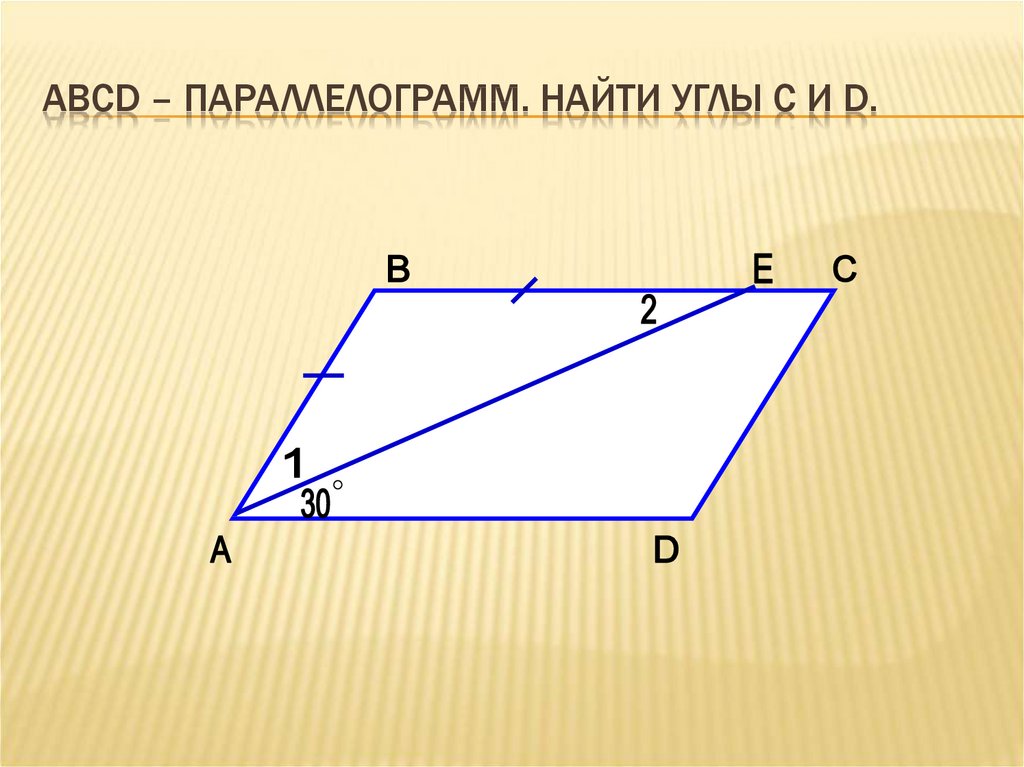
АВСD – ПАРАЛЛЕЛОГРАММ. НАЙТИ УГЛЫ С И D.

18. Найдите лишнюю фигуру

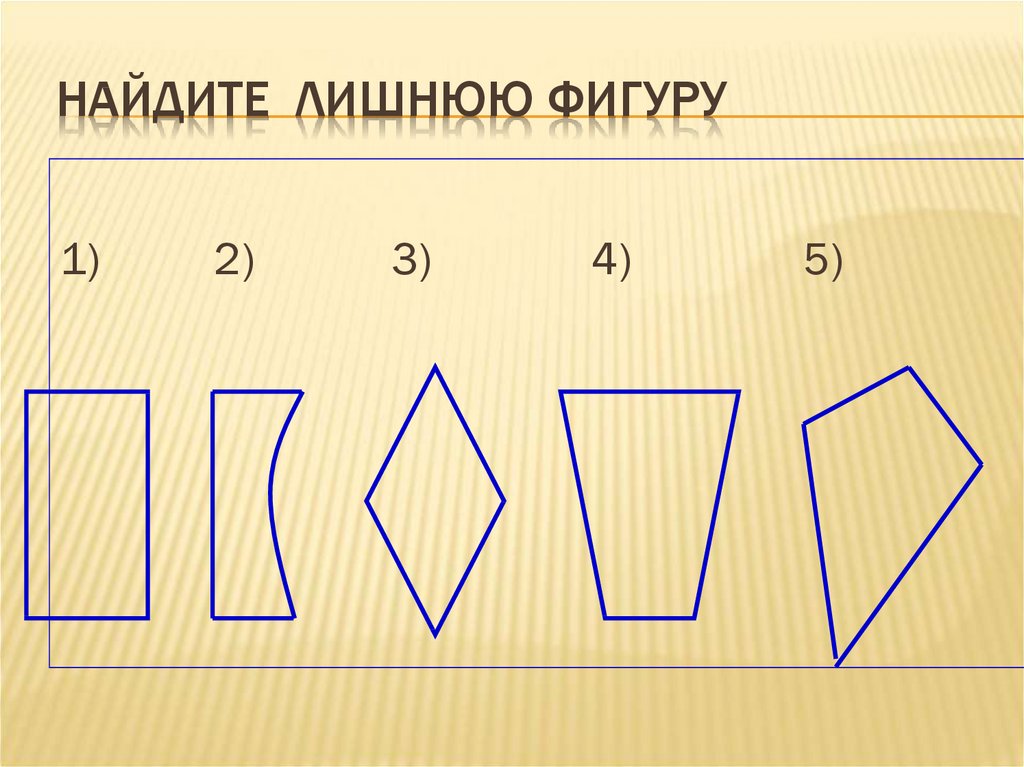
НАЙДИТЕ ЛИШНЮЮ ФИГУРУ
1)
2)
3)
4)
5)

19. Прямоугольник

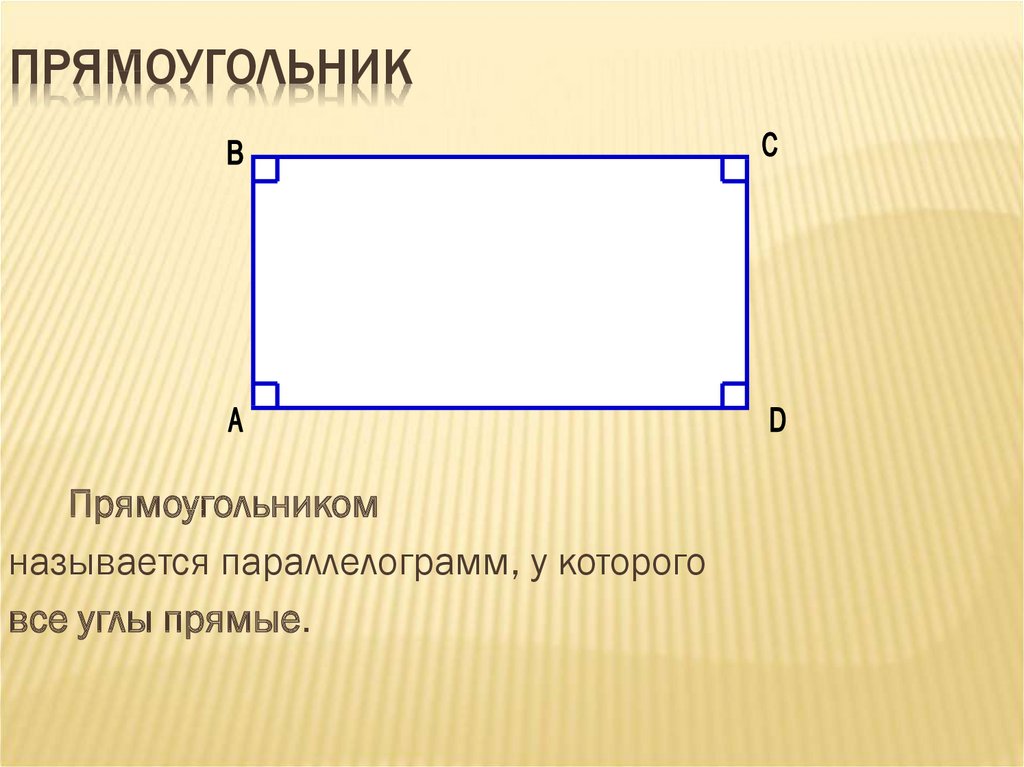
ПРЯМОУГОЛЬНИК
Прямоугольником
называется параллелограмм, у которого
все углы прямые.

20. Прямоугольник

ПРЯМОУГОЛЬНИК
Особое свойство прямоугольника:
Диагонали прямоугольника равны
Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот
параллелограмм - прямоугольник

21. Задача 1.

ЗАДАЧА 1.
Дано:
АВСD – прямоугольник.
АК - биссектриса ‫ ‬А .
ВК = 6 см, КС = 2 см.
Найти: Р
Решение: Т.к. АК - биссектриса ‫ ‬А, то ‫ ‬ВАК =
‫ ‬DАК = 45 (‫ ‬А=90 ), АВК – прямоугольный.
‫ ‬ВКА = 90 - ‫ ‬ВАК = 45 . Тогда АВК –
равнобедренный, значит, АВ = ВК = 6 см.
АD = ВС = ВК + КС = 6 + 2 = 8 см. Р = 2(АВ + АD)
= 28 см.
Ответ: 28 см.

22. Задача 2.

ЗАДАЧА 2.
Дано:
АВСD – прямоугольник.
‫ ‬CАD = 30 . АС = 14 см.
Найти: Р
Решение: АСD – прямоугольный, в нём ‫ ‬САD = 30 ,
значит, СD =АС/2 = 7см.Тогда АВ = СD = 7 см. В
прямоугольнике диагонали равны и точкой
пересечения делятся пополам, поэтому АО = АС/2 =
ВD/2 = ВО = 7 см. Р = АО + ВО + АВ = 7 + 7 + 7 = 21
см.
Ответ: 21 см.

23. Тест №1

ТЕСТ №1
1.
На каком из рисунков а) – в) изображен
прямоугольник?
а)
б)
в)

24. Тест №1

ТЕСТ №1
2. Если диагонали параллелограмма равны, то
он может быть:
а) любым параллелограммом;
б) прямоугольником;
в) любым четырехугольником.

25. Тест №1

ТЕСТ №1
3. Чему равна сумма углов прямоугольника?
а) 180
б) 90
в) 360
г) 720

26. Тест №1

ТЕСТ №1
4. Если одна сторона прямоугольника равна 10
см, а другая – 20 см, то его периметр равен:
а) 10 см;
б) 20 см;
в) 30 см;
г) 60 см;
д) 120 см.

27. Тест №1

ТЕСТ №1
5. Если стороны прямоугольника равны 3
см и 5 см, то какие это стороны?
а) смежные;
б) противоположные;
в) любые.

28. Тест №1

ТЕСТ №1
6. Сумма двух углов параллелограмма равна
100. Какие это углы?
а) любые;
б) противоположные;
в) соседние.

29. Тест №1

ТЕСТ №1
7. Составьте логическую цепочку, используя
понятия:
выпуклый многоугольник,
прямоугольник, параллелограмм,
четырёхугольник, многоугольник.

30. Самопроверка

САМОПРОВЕРКА
1.
2.
3.
4.
5.
6.
7.
б)
б)
в)
г)
а)
б)
Многоугольник выпуклый многоугольник
четырёхугольник параллелограмм
прямоугольник.

31. Домашнее задание. п. 45, вопросы 12-13, № 401(б), № 402.

ДОМАШНЕЕ ЗАДАНИЕ.
П. 45, ВОПРОСЫ 12-13,
№ 401(Б), № 402.