Similar presentations:
Односторонние пределы
1.
2.
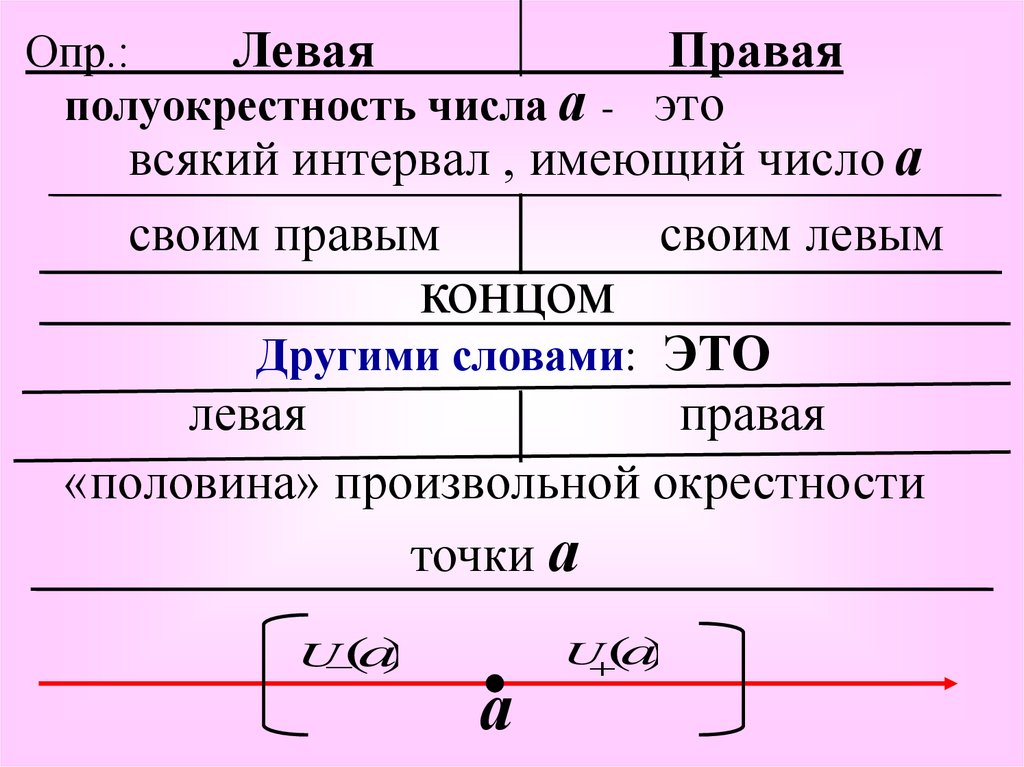
Опр.:Левая
Правая
полуокрестность числа а - это
всякий интервал , имеющий число а
своим правым
своим левым
концом
Другими словами: ЭТО
левая
правая
«половина» произвольной окрестности
точки а
U (a)
а
U (a)
3.
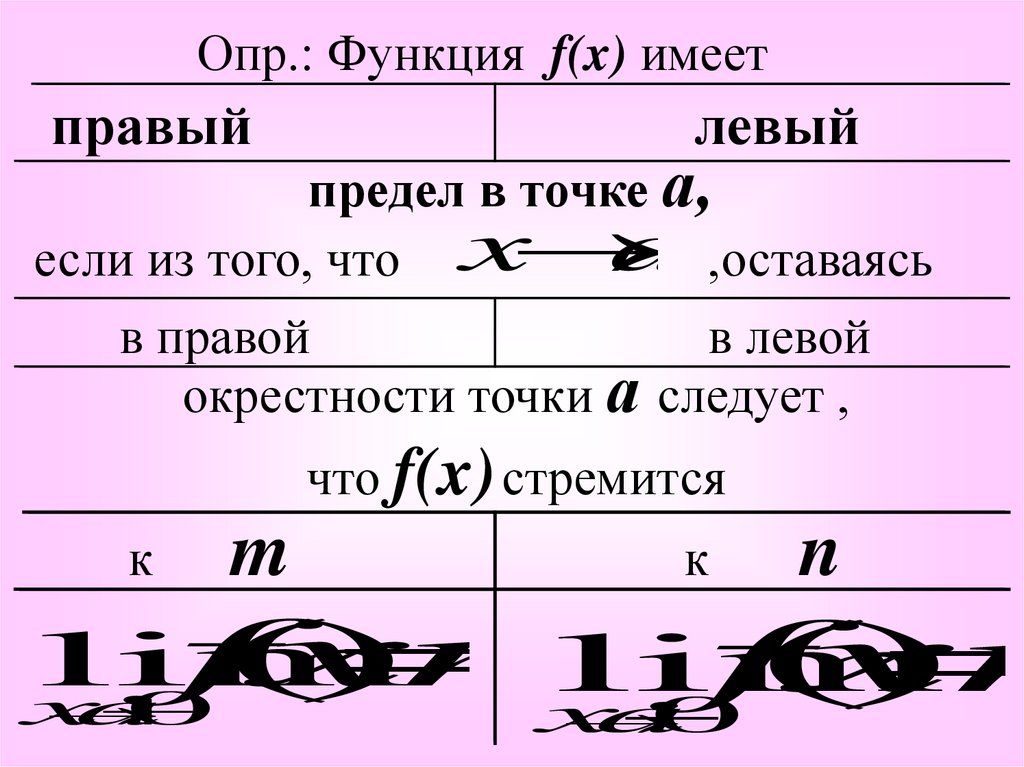
Опр.: Функция f(x) имеетправый
левый
предел в точке а,
a ,оставаясь
если из того, что x
в правой
в левой
окрестности точки а следует ,
что f(x) стремится
m
к
n
lim
f
(
x
)
m
lim
f
(
x
)
n
к
x
a
0
x
a
0
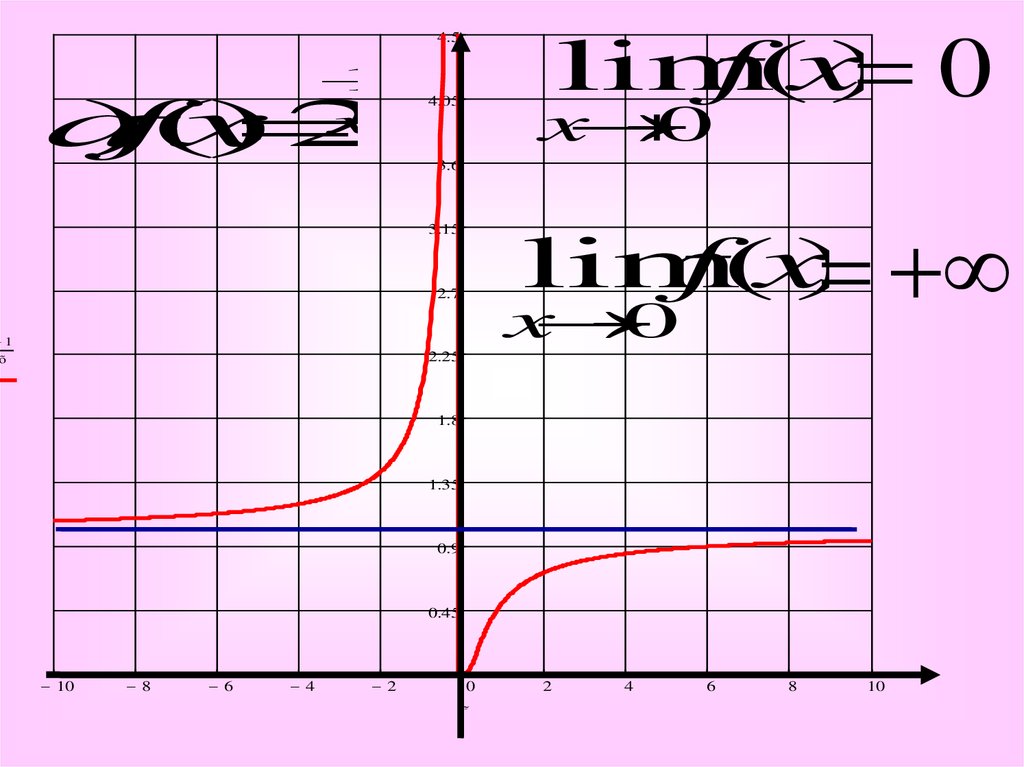
4.
limf(x) 0
4.5
1
x
а
)f(
x
)
2
x
0
4.05
3.6
lim
f(x)
3.15
x
0
2.7
1
2.25
õ
1.8
1.35
0.9
0.45
10
8
6
4
2
0
õ
2
4
6
8
10
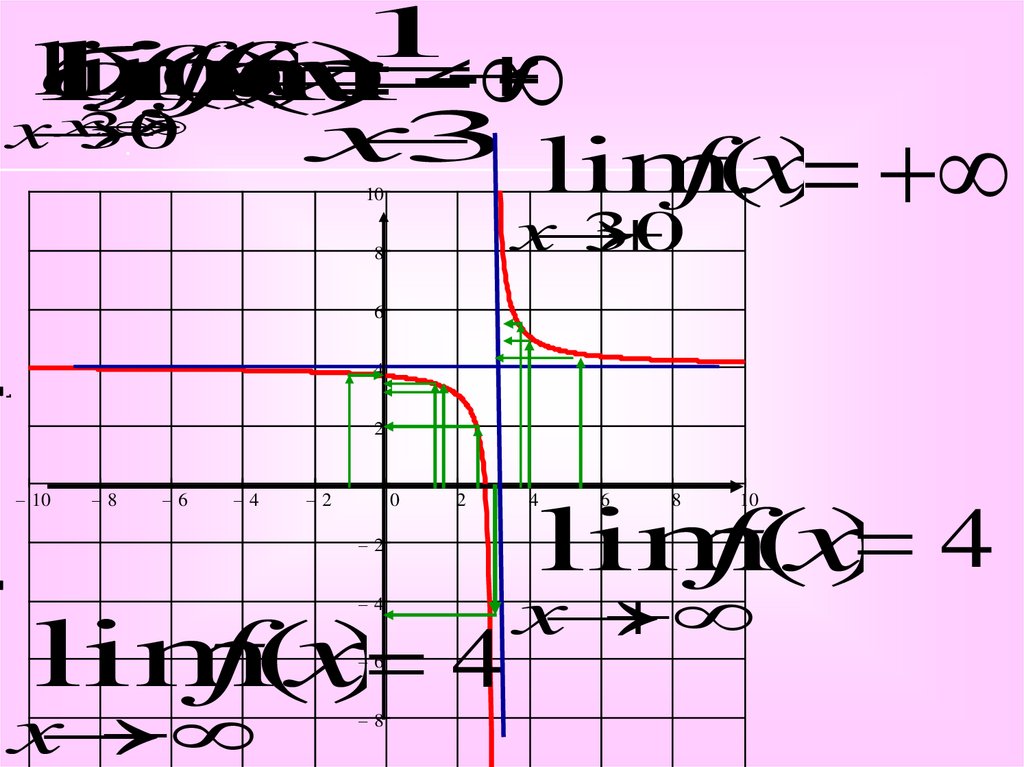
5.
1lim
ff
(
x
))
б
)f(
x
)
4
lim
(
x
4
x
x
3
0
x
3 lim
f(x)
10
x
3 0
8
6
4
2
10
8
6
4
2
0
2
2
4
lim
f(x) 4
6
x
8
lim
f(x) 4
4
6
8
10
x
6.
Опр.: Если существуютправый и левый пределы функции
в точке a и они равны одному и
тому же числу b,
то данная функция f(x) имеет
предел в точке a равный b.
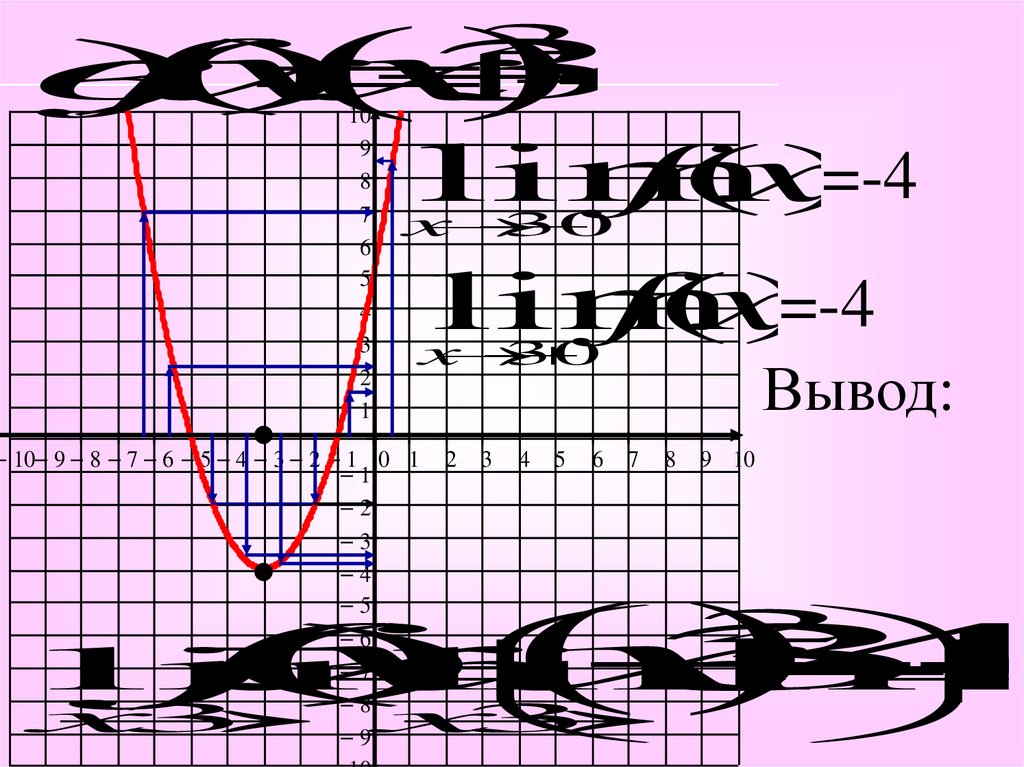
7.
в)
f
(
x
)
x
3
4
2
10
9
8
7
6
5
4
3
2
1
=-4
lim
f
(
x
)
x
3
0
=-4
lim
f
(
x
)
x
3
0
10 9 8 7 6 5 4 3 2 1 0 1
1
2
3
4
5
6
7
8
9
Вывод:
2
3
4
5
6
7
8
9 10
lim
f
(
x
)
lim
x
3
4
4
x
3
x
3
2
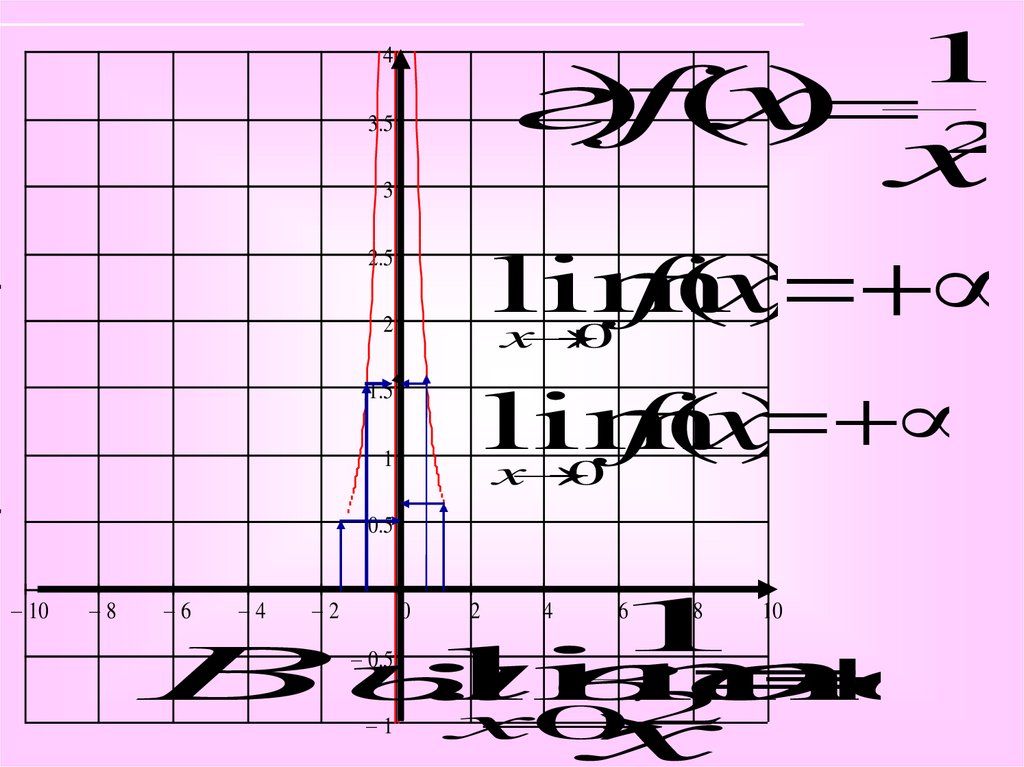
8.
1г
)f(x
) 2
4
3.5
x
lim
f(x)
3
2.5
x
0
2
lim
f
(
x
)
x
0
1.5
1
0.5
10
8
6
4
2
1
Вывод
:
lim
2
x
0
x
0
0.5
1
2
4
6
8
10
9.
Опр.: Точка а называетсяточкой разрыва функции f(x),
если
1) точка а является точкой
прикосновения для области
определения функции f(x),
НЕ является
непрерывной в точке а.
2) функция f(x)
10. Классификация точек разрыва.
1) Точка а называетсяточкой разрыва I рода (скачок),
если функция в этой точке имеет
КОНЕЧНЫЕ
ОДНОСТОРОННИЕ пределы;
если односторонние пределы
равны между собой,
то точка разрыва называется
устранимой.
11.
2) Точкаа называется
точкой разрыва II рода ,
если хотя бы один
из односторонних пределов
бесконечен или не существует
Смотри примеры:
1
x
1
а
)f(
x
)
2 г
)f(x
) 2
x
12.
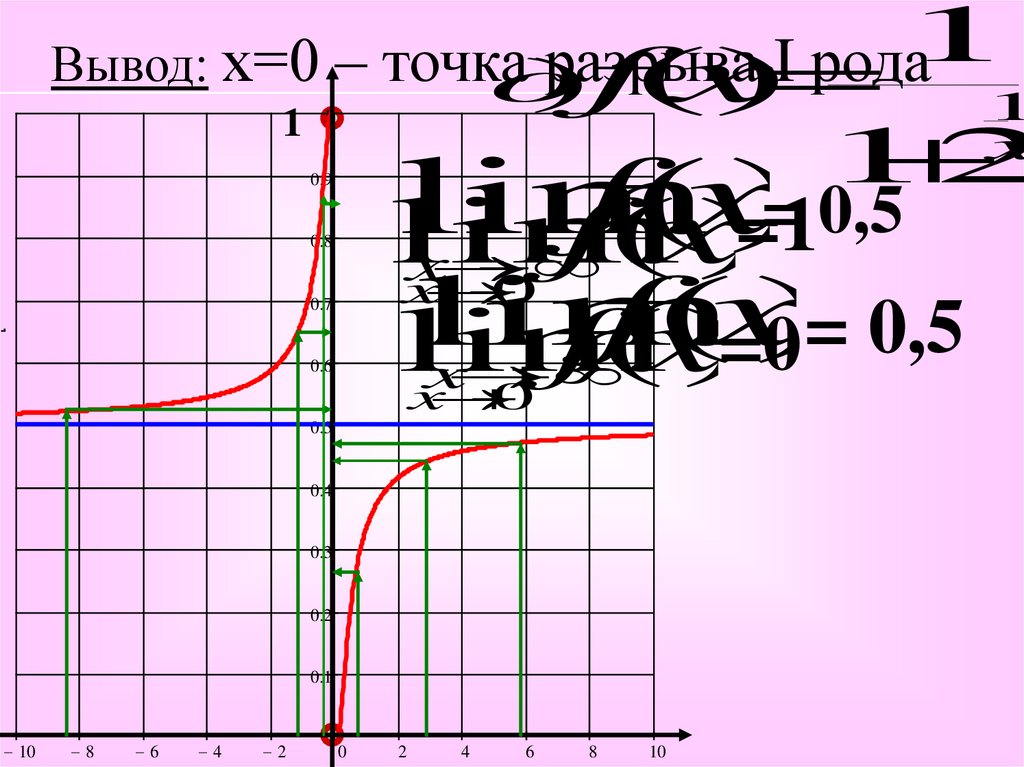
Вывод: х=01
1
1
– точка
разрыва
I
рода
д
)f(
x
)
1
2
=
0,5
lim
f
(
x
)
=1
lim
f(x
)
x
0.9
0.8
x
0
lim
f
(
x
)
=
0,5
=0
lim
f(x)
x
0.7
0.6
x
0
0.5
0.4
0.3
0.2
0.1
10
8
6
4
2
1
x
0
2
4
6
8
10
13.
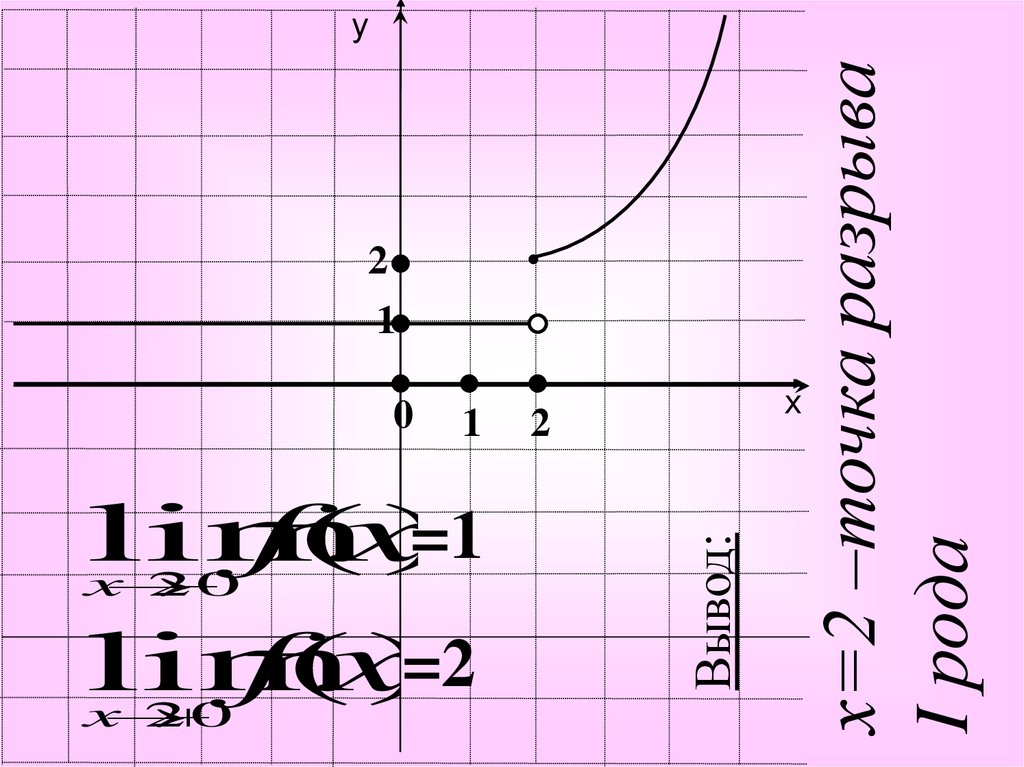
21
1
=1
lim
f
(
x
)
x
2
0
=2
lim
f
(
x
)
x
2
0
х
2
Вывод:
0
х=2 –точка разрыва
I рода
у
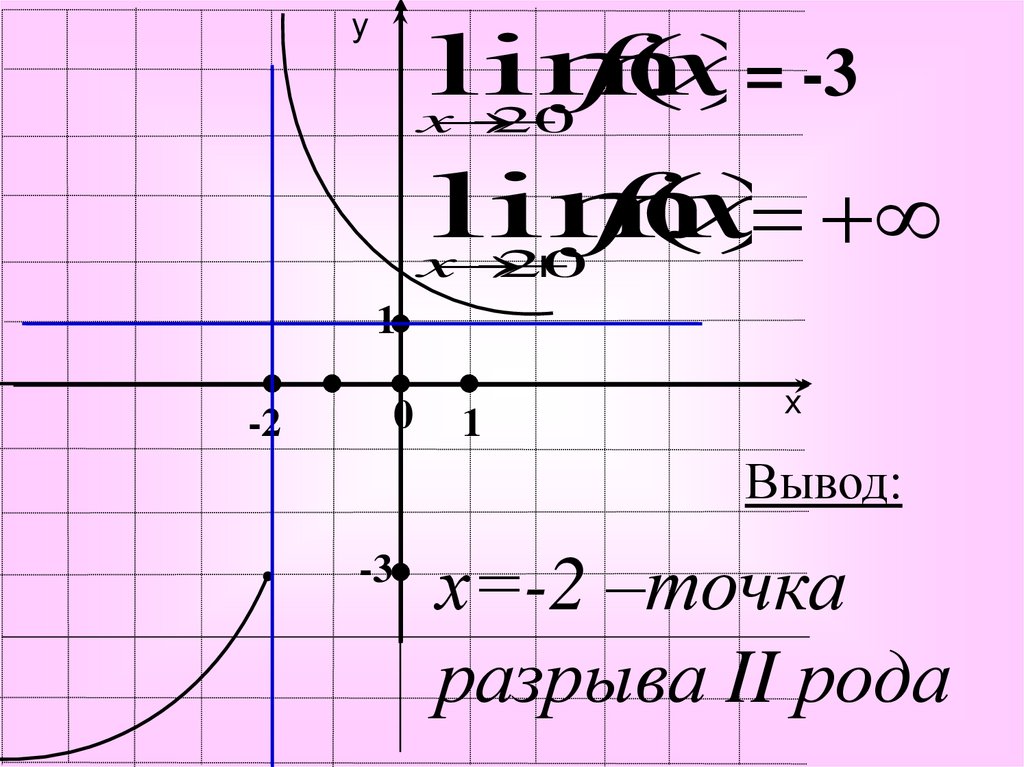
14.
уlim
f
(
x
)
= -3
x
2
0
lim
f
(
x
)
x
2
0
1
0
-2
1
х
Вывод:
-3
х=-2 –точка
разрыва II рода
15.
ух
16.
Знание того, какими вещи должны быть,характеризует человека умного;
знание того, каковы вещи на самом деле,
характеризует человека опытного;
знание же того, как их изменить к лучшему,
характеризует человека гениального.
(Дидро Д.)






 mathematics
mathematics








