Предел функции в точке

1. Предел функции в точке

Опр. Если при приближении аргумента x к числу a
значения функции f(x) приближаются к
некоторому числу A, то число А называют
пределом функции f(x) в точке a
Обозначение
lim f ( x) A.
x a

2. Предел функции в точке

Опр. Если при приближении аргумента x к числу a
значения функции f(x) бесконечно возрастают,
то говорят, что
lim f ( x) ,
x a
если бесконечно убывают, то
lim f ( x) ,
x a

3. Предел функции в точке

Опр. Если при приближении аргумента x к числу a
с одной стороны значения функции f(x)
бесконечно возрастают, а сдругой стороны
бесконечно убывают, то говорят, что
lim f ( x) ,
x a

4.

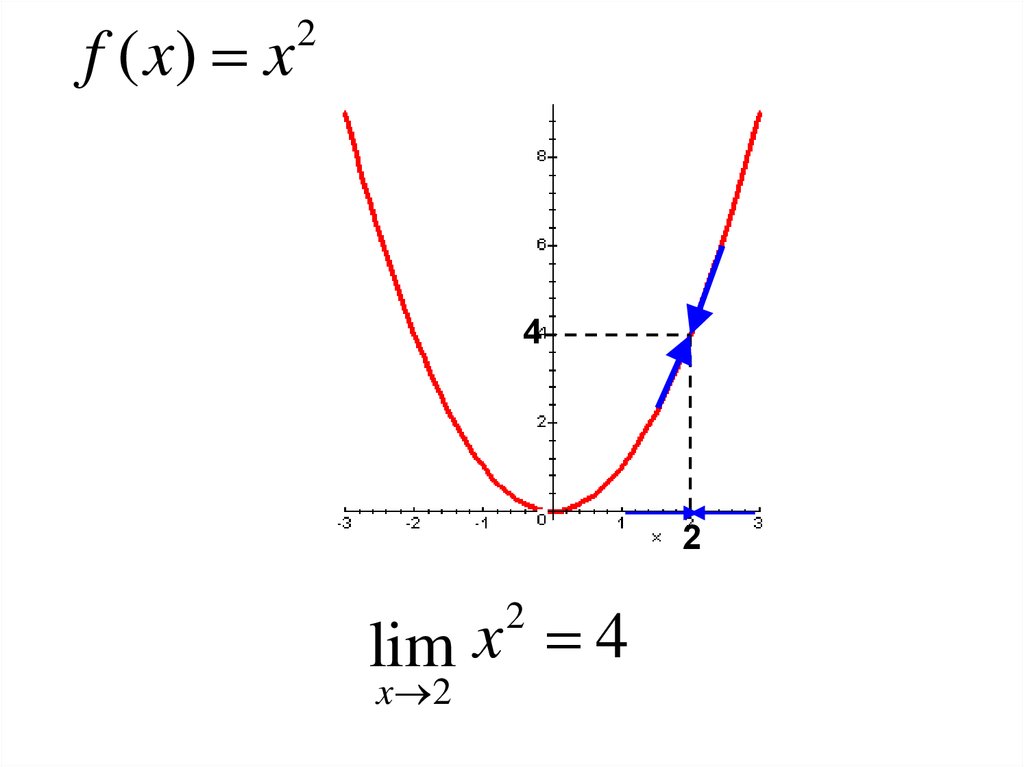
f ( x) x
2
4
2
lim x 4
2
x 2

5.

1
f ( x)
x 1
1
1
lim
x 1 x 1

6.

x 1
f ( x)
x 1
2
f ( x) x 1, x 1
2
1
lim f ( x) 2
x 1

7. Предел функции в точке

Если график функции не разрывается в точке a, то
lim f ( x) f (a).
Если разрывается, то
x a
необходимы дополнительные исследования.

8.

Пример 1.
x 2 25
?
lim
x 5 x 5

9.

Пример 1.
x 2 25 0
lim
x 5 x 5
0

10.

Пример 1.
x 2 25 0
( x 5)( x 5)
lim( x 5) 10
lim
lim
x 5 x 5
x 5
x 5
0 x 5

11.

Пример 2.
x2 6 x 5
?
lim 2
x 1 x 5 x 4

12.

Пример 2.
x2 6 x 5 0
lim 2
x 1 x 5 x 4
0

13.

Пример 2.
x2 6 x 5 0
( x 1)( x 5)
( x 5) 4 4
lim 2
lim
lim
x 1 x 5 x 4
0 x 1 ( x 1)( x 4) x 1 ( x 4) 3 3

14.

Пример 3.
x3 27
lim
2
x 3 9 x