Преобразование электрических цепей

1. Конспект лекций по электротехнике Подготовлен: Степановым К.С., Беловой Л.В., Кралиным А.А., Панковой Н.Г. Кафедра

теоретической и общей
электротехники.
Лекция 3

2. Преобразование электрических цепей

3. Последовательное соединение сопротивлений

Второй закон Кирхгофа для этой схемы
имеет вид U = UR1 + UR2 + UR3 .
Поделим почленно это уравнение на ток
I. U/I = UR1 /I + UR2 /I + UR33 /I,
получим R = R1+ R2+ R3

4.

5. Последовательное соединение сопротивлений

• Таким образом,
при последовательном соединении
сопротивлений эквивалентное
сопротивление равно сумме
последовательно соединенных
сопротивлений R, а эквивалентное
сопротивление всегда получается
больше наибольшего.

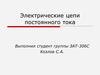
6. Параллельное соединение сопротивлений

I
U
R1
R2
R3
I1
I2
I3

7. Параллельное соединение сопротивлений

• Первый закон Кирхгофа для этой схемы
выглядит так:
I = I1+ I2 + I3 .
• По закону Ома: I = U/Rэ ,
I1 = U/R1, I2 = U/R2 , I3 = U/R3.
Тогда: U/RЭ = U/R1+U/R2+U/R3 и
1/RЭ = 1/R1+1/R2+1/R3 ,
GЭ = G1+G2+G3.

8. Параллельное соединение сопротивлений

• Таким образом, при параллельном
соединении сопротивлений
эквивалентная проводимость равна
сумме проводимостей, а выражение для
эквивалентного сопротивления имеет вид:
R1 R2 R3
RЭ =
.
R1 R2 R2 R3 R1 R3
Эквивалентное сопротивление всегда
получается меньше наименьшего.

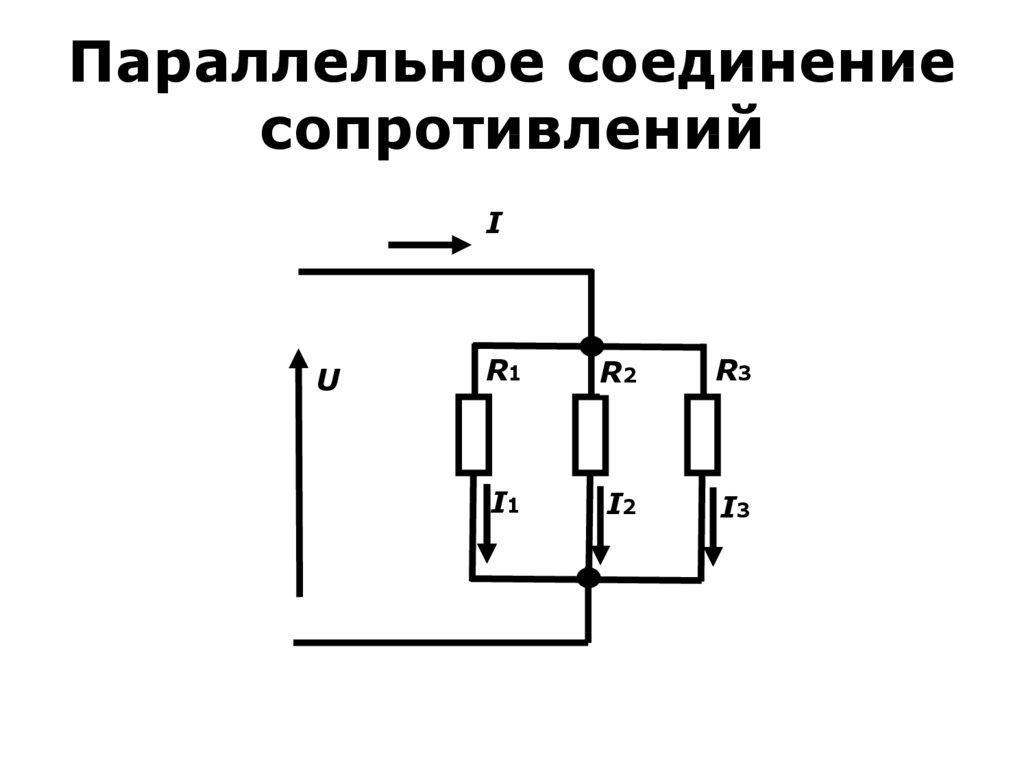
9. Смешанное соединение сопротивлений

• Иногда нельзя определить параллельно
или последовательно соединены
сопротивления. Например, как
показано на нижеприведенной схеме.

10. Смешанное соединение сопротивлений

Rab
a
b
R1
d
Rde
Rfd
Rbc
Rca
Ref
R2
c
R3
f
E
e

11. Смешанное соединение сопротивлений

В этом случае заменим треугольник
abc звездой abc с соблюдением
условия эквивалентности - так
чтобы параметры (токи ветвей
и межузловые напряжения)
схемы вне преобразуемой цепи
остались без изменения.

12. Замена треугольника эквивалентной зездой

b
R1
d
Rb
a
Ra
Rd
Re
O
R2
Rc
Rf
f
c
R3
E
e

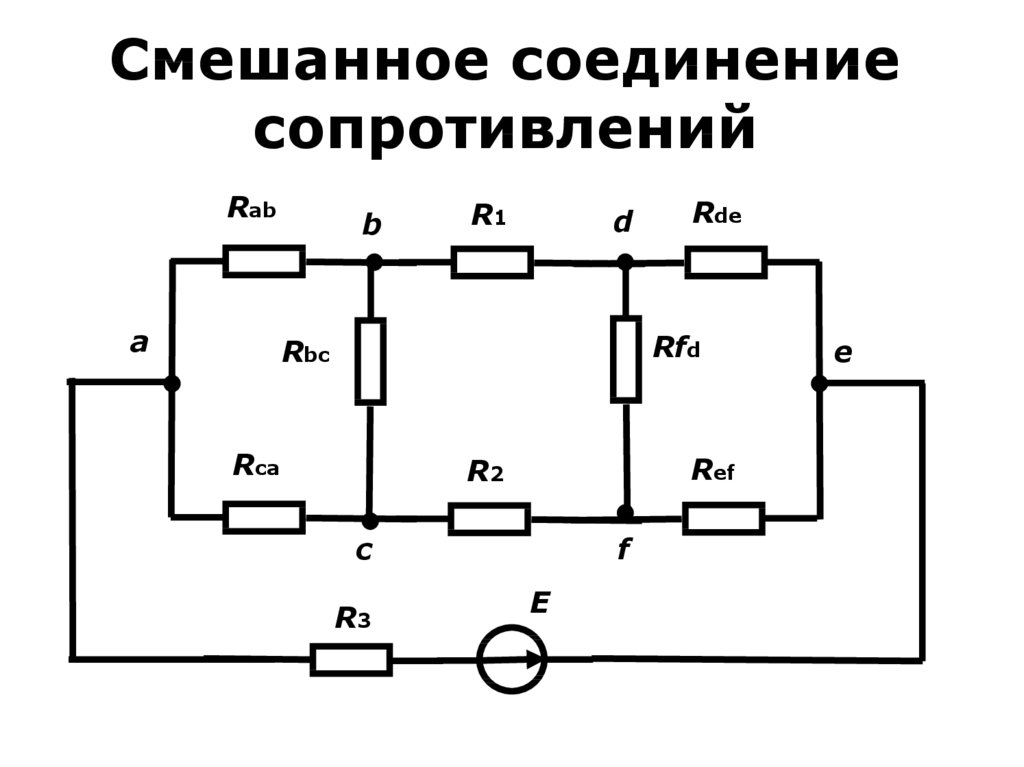
13. Замена треугольника эквивалентной звездой

a
Ia
Ia
Ra
a Ia
Rca
Rab
≡
O
Rbc
Rb
Rc
c
b
Ic
Ic
Ib
c
Ic
b
Ib

14. Замена треугольника эквивалентной звездой

• Ia=0
Rb+Rc=Rbc (Rab+Rca)/(Rab+Rbc+Rca) (1)
• Ib=0
Ra+Rc=Rca (Rab+Rbc)/(Rca+Rab+Rbc) (2)
• Ic=0
Ra+Rb=Rab (Rbc+Rca)/(Rab+Rbc+Rca) (3)
• Решая систему относительно Ra, Rb,
Rc . Находим их выражения

15. Замена треугольника эквивалентной звездой

• Ra=Rab Rca/(Rab+Rbc+Rca) (4)
• Rb=Rbc Rab/(Rca+Rab+Rbc) (5)
• Rc=Rca Rbc/(Rab+Rbc+Rca) (6)
• Для замены звезды треугольником
надо решить систему уравнений
4,5,6 относительно Rab, Rbc и Rсa:

16. Замена звезды эквивалентным треугольником

• Rab=Ra+Rb+RaRb/Rc
(7)
• Rdc=Rb+Rc+RbRc/Ra
(8)
• Rca =Ra+Rc+RaRc/Ra
(9)

17. Преобразование активных элементов

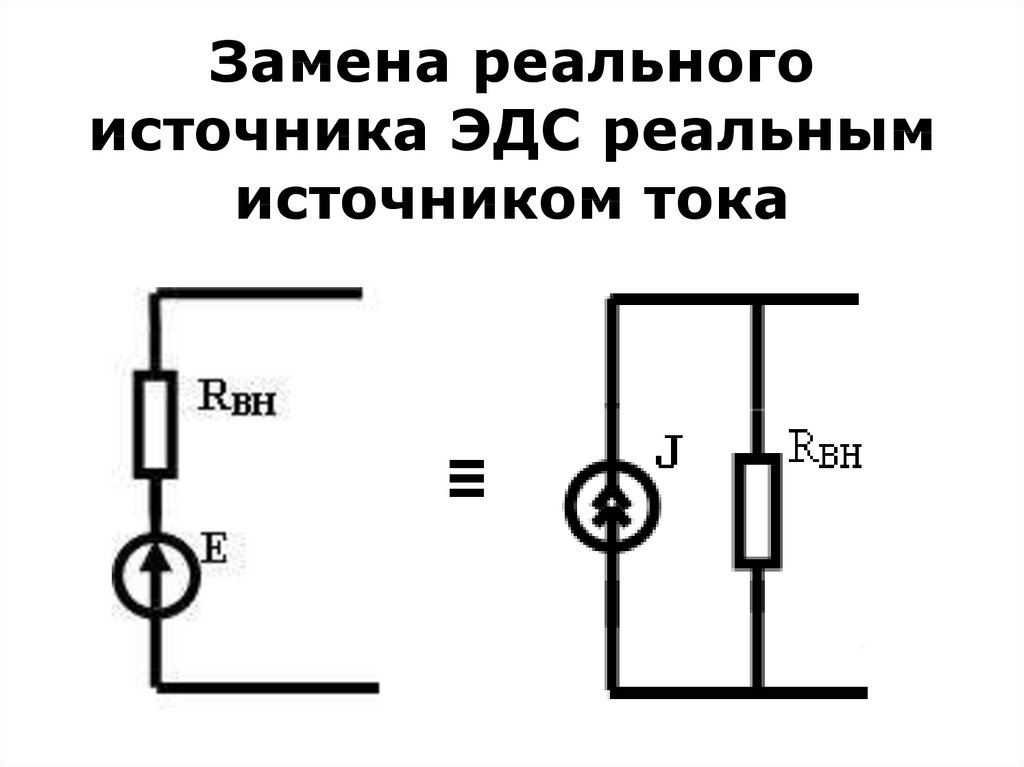
18. Замена реального источника ЭДС реальным источником тока

• Источник ЭДС можно получить из
источника тока, если последовательно
с источником ЭДС (E = J*RBH)
включить сопротивление, равное
внутреннему сопротивлению источника
тока. Соответственно значение тока
источника тока определяют по формуле
J = E/RВН.

19. Замена реального источника ЭДС реальным источником тока

≡

20. Теорема об эквивалентном источнике ЭДС

• Теорема Гельмгольца – Те Ве Нена.
- Активный двухполюсник по
отношению к рассматриваемой цепи
можно заменить эквивалентным
источником напряжения, ЭДС которого
равна напряжению холостого хода на
зажимах этой ветви, а внутренне
сопротивление равно входному
сопротивлению двухполюсника.

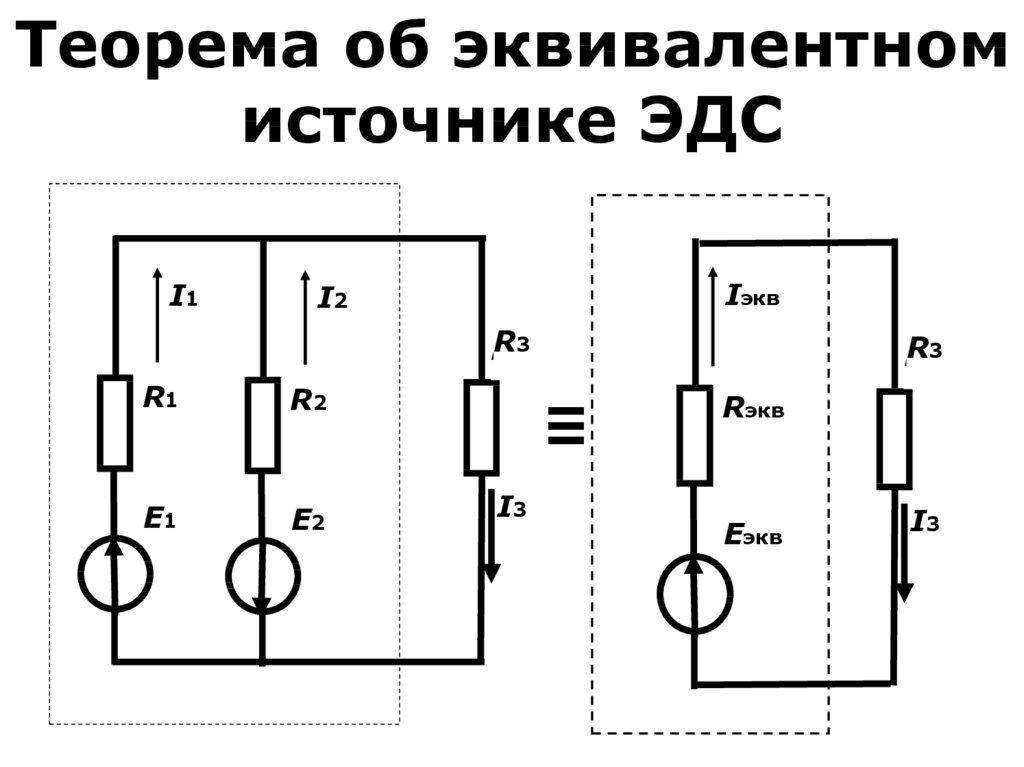
21. Теорема об эквивалентном источнике ЭДС

I1
Iэкв
I2
R23
R
R1
R2
E1
E2
R23
R
≡
I3
Rэкв
Eэкв
I3

22. Теорема об эквивалентном источнике ЭДС

• Eэк=(E1 G1 - E2 G2)/(G1+G2)=Uxx,
где G - проводимость, G=1/R
• Rэкв = R1R2/(R1+R2)= Rвх12
• Iэк = I3 = Eэк/(Rэкв + R3)

23. Теорема об эквивалентном источнике тока

• Теорема Нортона.
• Активный двухполюсник по
отношению к рассматриваемой ветви
можно заменить эквивалентным
источником тока, ток которого равен
току в этой ветви, замкнутой
накоротко, а внутренняя проводимость
источника – входной проводимости
источника.

24. Теорема об эквивалентном источнике тока

I
I
a
A
Uab
Jk
Gвх
Gн
a
Gн
Uab
b
b
I = IkGвх/(Gвх + Gн)
Ik
A
a
Gн
a
П
Gвх
ъ
b
b

25. Режимы работы реального источника ЭДС

26. Режим холостого хода

I
A
V2
Uн
Uвн
V1
Uи
Rвн
E
S
V3
Rн

27. 1. Режим холостого хода

• Ключ S разомкнут,
• Напряжение холостого хода на выходе
источника равно его ЭДС (UХХ = E),
• ток холостого хода равен нулю
(IХХ = 0),
• сопротивление нагрузки равно
бесконечности (RН = ),
• коэффициент полезного действия (К.П.Д.)
при идеальном источнике ЭДС в этом режиме
стремится к единице ( = 1).

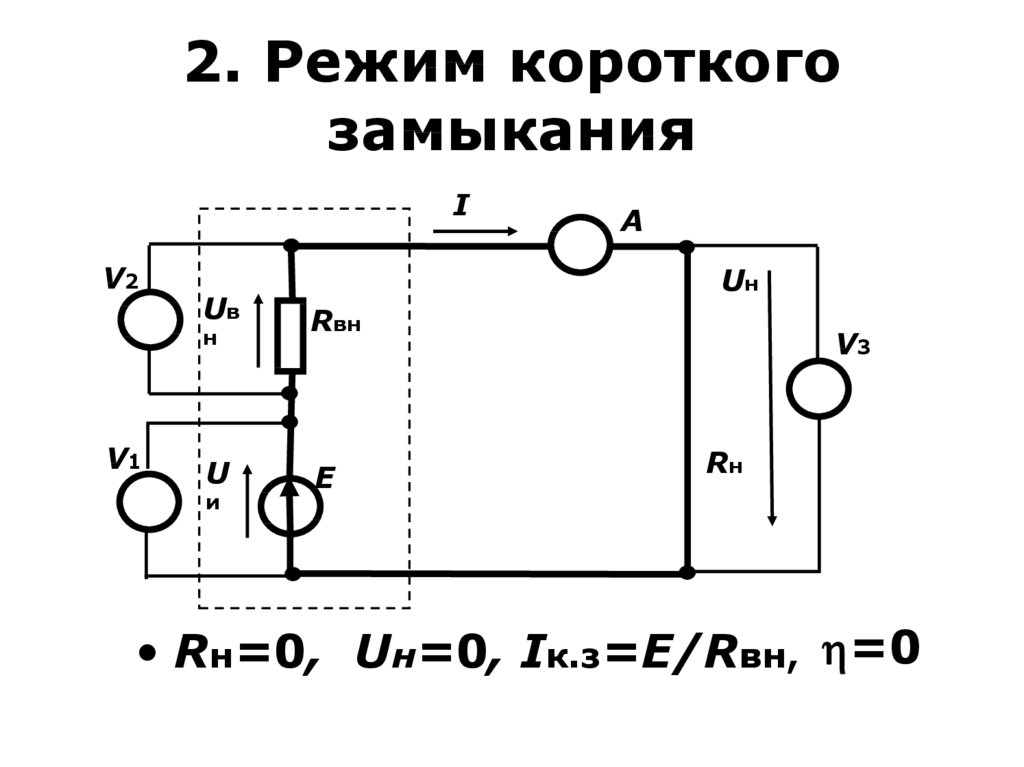
28. 2. Режим короткого замыкания

I
V2
Uв
н
V1
U
и
A
Uн
Rвн
E
V3
Rн
• Rн=0, Uн=0, Iк.з=E/Rвн, =0

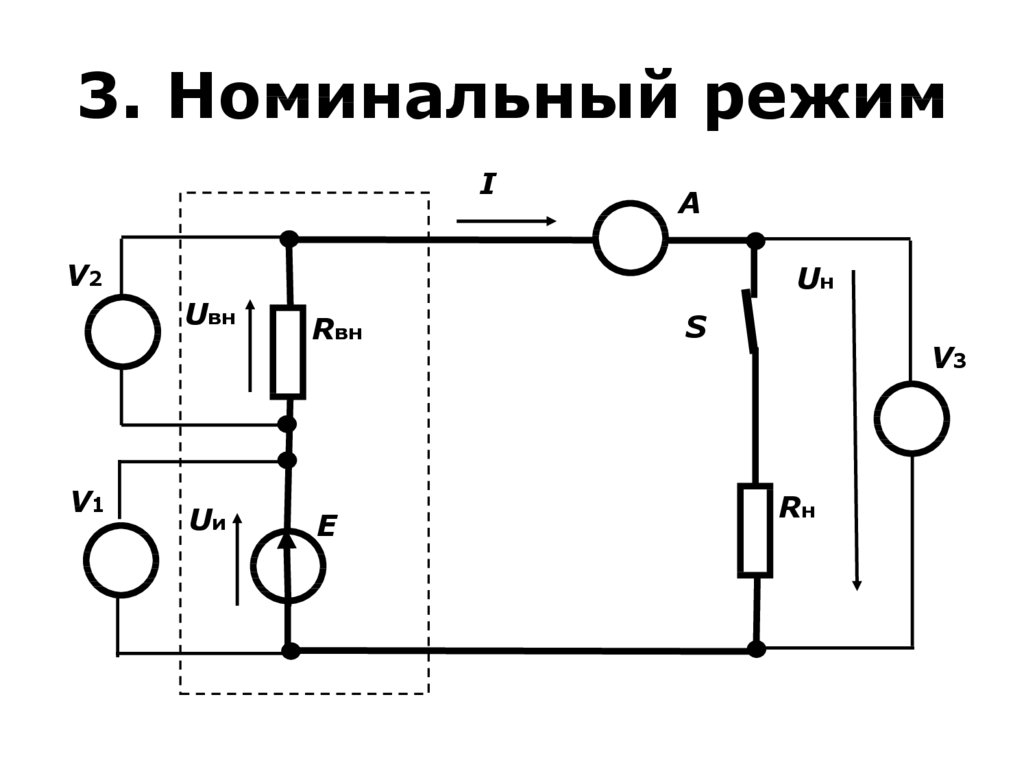
29. 3. Номинальный режим

• режим, на который рассчитывается
источник, (ключ S замкнут). В этом
режиме источник Е работает
эффективно с точки зрения
надёжности и экономичности.
E
, UВЫХ = UНОМ ,
IН = IНОМ =
Rвн Rн
=
Pн
Е 2 Rн
(Rвн Rн)
Rн
1
2
2
Pи (Rвн Rн)
Е
Rвн Rн 1 Rвн
Rн
< 1.

30. 3. Номинальный режим

I
A
V2
Uн
Uвн
V1
Uи
Rвн
E
S
V3
Rн

31. 4. Согласованный режим

- это режим, при котором в нагрузку
отдаётся максимальная мощность.
Мощность источника: PИ=E I.
Мощность нагрузки
PН=UНАГР IНАГР=I2нагр Rн.
E
IНАГР = Rвн Rн , тогда
E
PН = (
)2 RН
Rвн Rн

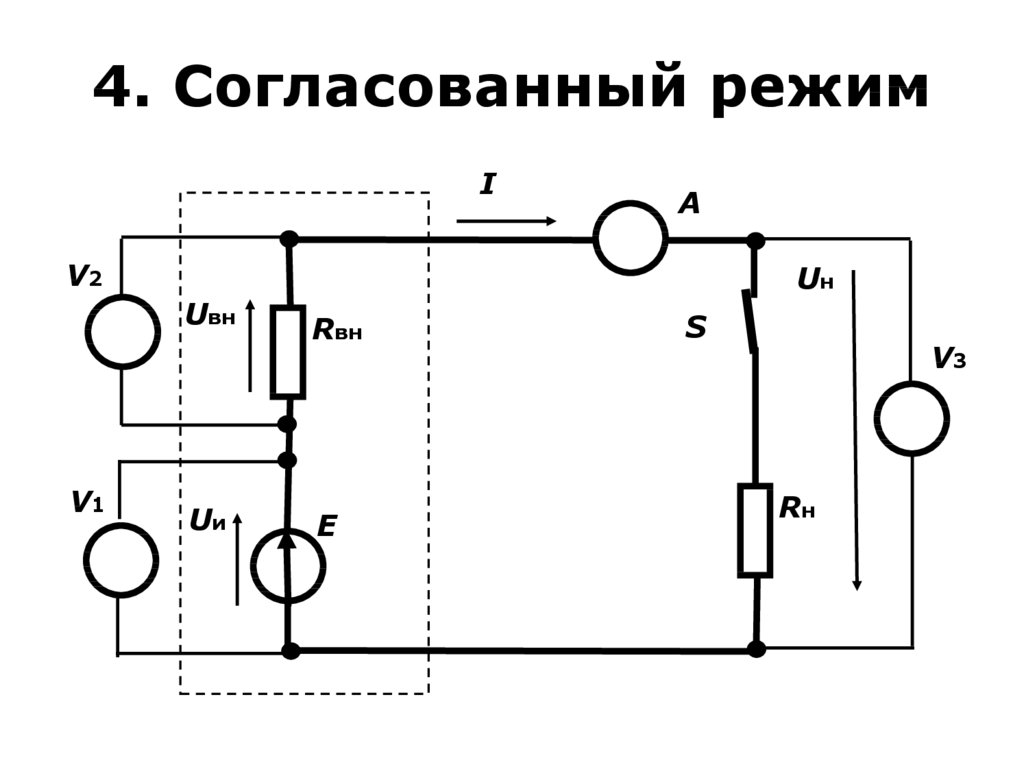
32. 4. Согласованный режим

I
A
V2
Uн
Uвн
V1
Uи
Rвн
E
S
V3
Rн

33. 4. Согласованный режим

• Вопрос: «При какой величине RН
мощность в нагрузке будет иметь
максимальное значение?», т.е.
нужно определить экстремум
функции. Для этого возьмем
PH
частную производную
=0
RH

34. 4. Согласованный режим

• К.П.Д:
= Pн/Pи =
=[E2 Rн/(Rвн+Rн)2]·[(Rвн+Rн)/E2] =
=Rн (Rн+Rвн) = 1/(1+Rвн/Rн) = 0,5.

35. 4. Согласованный режим

• Таким образом в согласованном
режиме:
• Rн = Rвн;
• Pнагр = Pmax = Pист/2;
• Uн = E/2;
• Iн = Iк.з/2;
• = 0.5

36. Зависимость мощностей источника, приемника и потерь от тока.

P
Pи
0
∆P
Pн
Iсогл
I
Iкз

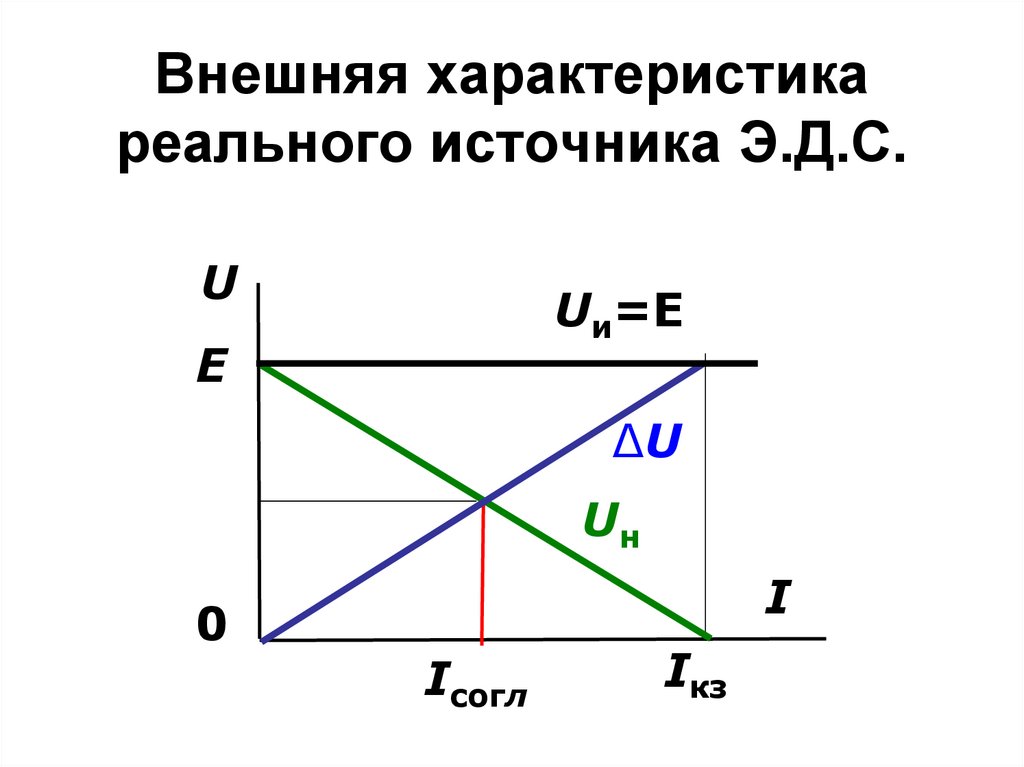
37. Внешняя характеристика реального источника Э.Д.С.

U
Uи=E
E
∆U
Uн
0
I
Iсогл
Iкз

38. Благодарю за внимание