Задачи по планиметрии

1. Задачи по планиметрии

№ 16
Презентацию составила:
учитель МКОУ СШ № 2 г.Котельниково
Куницына А.В.

2. Задача №1

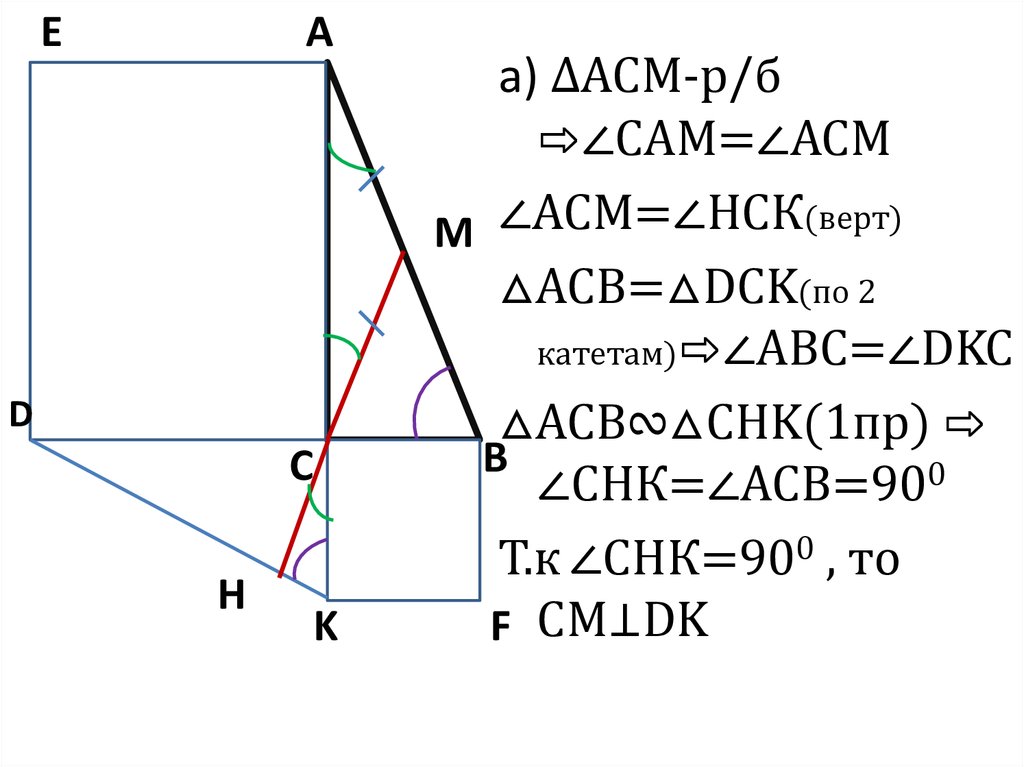
На катетах АС и ВС прямоугольного
треугольника АВС вне треугольника
построены квадраты ACDE и BFKC. Точка М –
середина гипотенузы АВ, Н – точка
пересечения прямых СМ и DK.
а) Докажите, что CM⊥DK.
б) Найдите МН, если известно, что катеты
треугольника АВС равны 6 и 8.

3.

E
A
D
C
H
K
а) ∆АСМ-р/б
⇨∠САМ=∠АСМ
M ∠АСМ=∠НСК(верт)
△АСВ=△DCK(по 2
катетам)⇨∠АВC=∠DKC
△ACB∾△CHK(1пр) ⇨
B
∠СНК=∠АСВ=900
Т.к ∠СНК=900 , то
F СМ⊥DK

4.

E
A
б) МН=СМ+СН
СМ=½АВ=5
M
СН=
D
C
H
K
B
F
DC CK 6 8
4,8
DK
10
МН=9,8

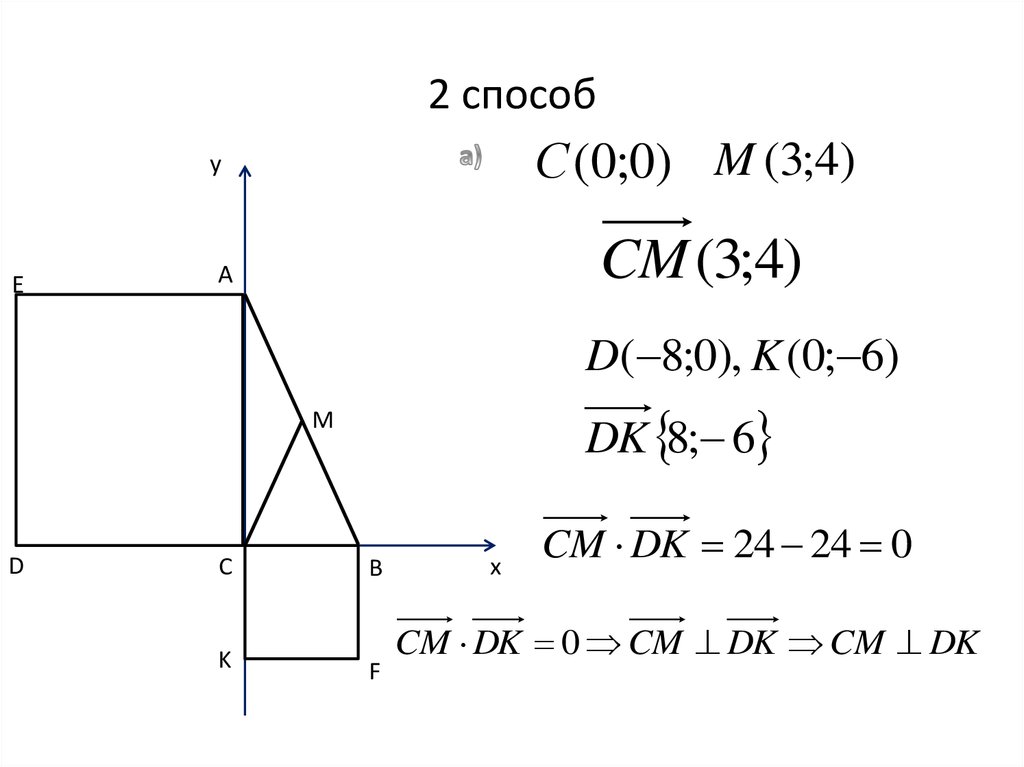
5. 2 способ

С (0;0) M (3;4)
у
Е
CM (3;4)
А
D( 8;0), K (0; 6)
DK 8; 6
M
D
С
K
В
F
х
CM DK 24 24 0
CM DK 0 CM DK CM DK

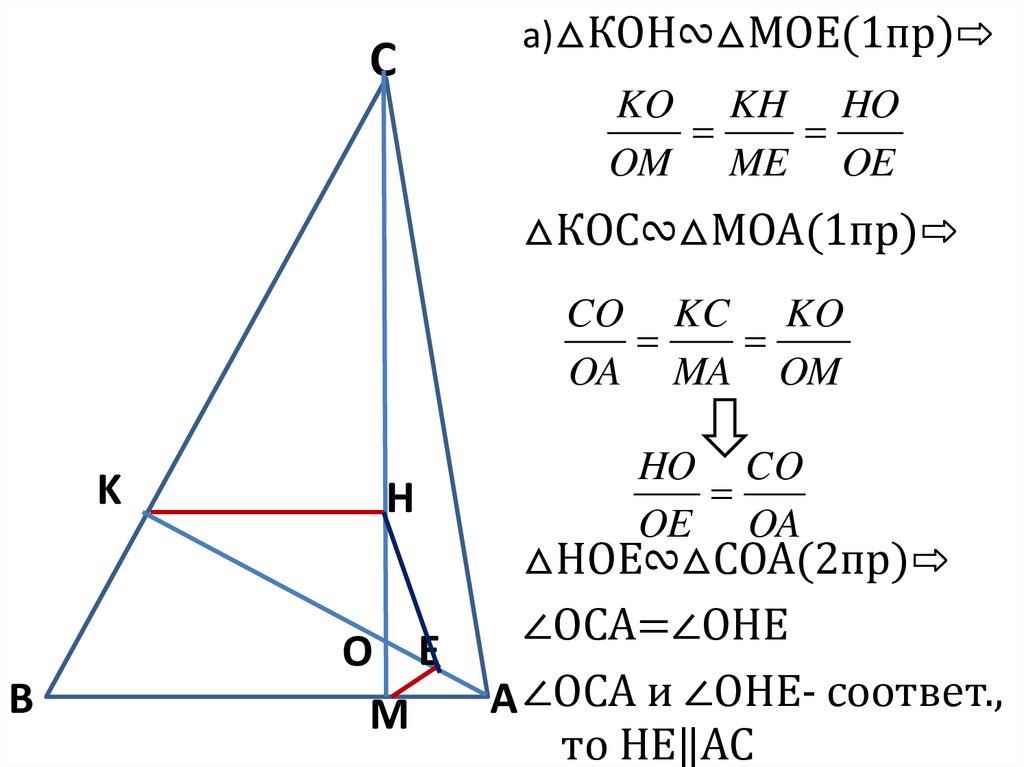
6. Задача №2

В остроугольном треугольнике АВС
проведены высоты АК и СМ. На них из
точек М и К опущены перпендикуляры МЕ и
КН соответственно.
а) Докажите, что ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если ∠АВС=300.

7.

C
а)△КОН∾△МОЕ(1пр)⇨
KO KH HO
OM ME OE
△КОС∾△МОА(1пр)⇨
CO KC KO
OA MA OM
K
B
H
O E
M
HO CO
OE OA
△НОЕ∾△СОА(2пр)⇨
∠ОСА=∠ОНЕ
A ∠ОСА и ∠ОНЕ- соответ.,
то НЕ‖АС

8.

б)Т.к. △НОЕ∾△СОА, то
C
EH OH
AC OC
∠СКН=∠САВ=30
СК=х, тогда СН=½х
∠КОС=30 ⇨СО=2х
ОН=2х-½х=1,5х
K
B
H
O E
M
EH OH 1,5 x 3
AC OC
2x 4
A

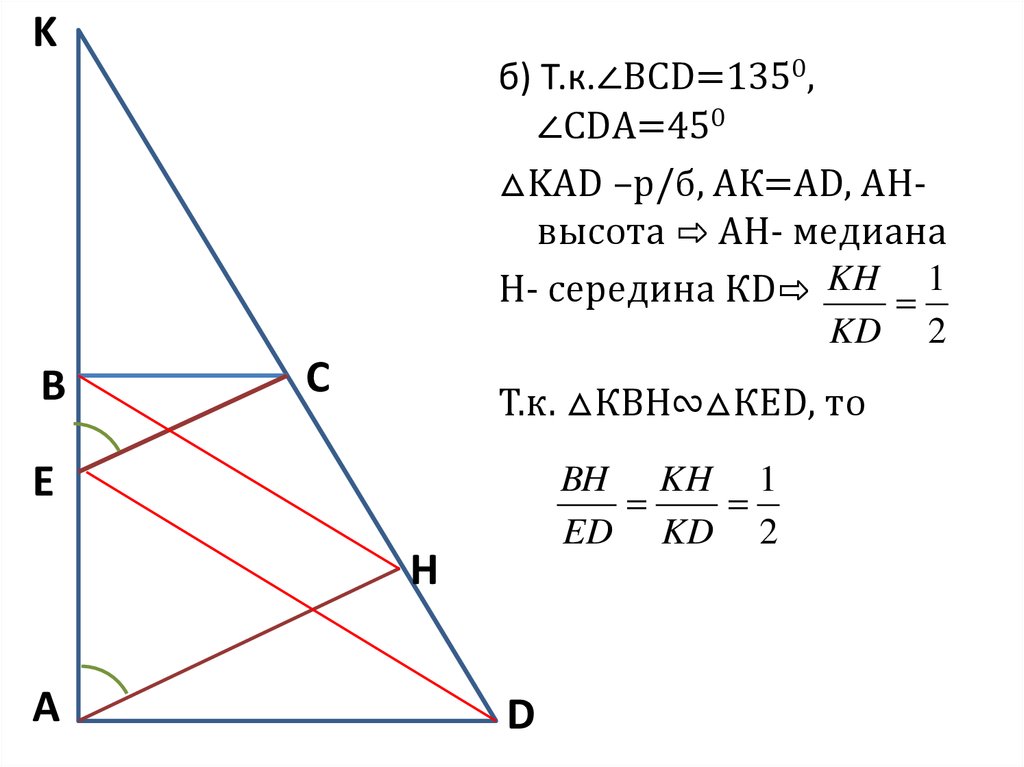
9. Задача №3

В трапеции ABCD боковая сторона АВ
перпендикулярна основанию AD. Из точки А
на сторону CD опустили перпендикуляр АН.
На стороне АВ отмечена точка Е так, что
прямые CD и СЕ перпендикулярны.
а) Докажите, что ВН и ED параллельны.
б) Найдите отношение ВН:ЕD, если
∠BCD=1350.

10.

K
а) △КВС∾△KAD(1пр)⇨
KB KC
a
KA KD
КВ=a⋅АК, КС=a⋅KD
△КEС∾△KAH(1пр)⇨
B
KE KC
b
KA KH
C
КЕ=b⋅КА, КС=b⋅КН
E
H
A
KB a AK a
KE b KA b
KH a
KD b
△КВН∾△КВD(2пр)⇨
∠КНВ=∠KDE, соотв., то
D ВН‖ED

11.

K
б) Т.к.∠BCD=1350,
∠CDА=450
△KAD –р/б, АК=АD, АНвысота ⇨ АН- медиана
Н- середина КD⇨ KH 1
KD
B
C
Т.к. △КВН∾△КЕD, то
E
BH KH 1
ED KD 2
H
A
D
2

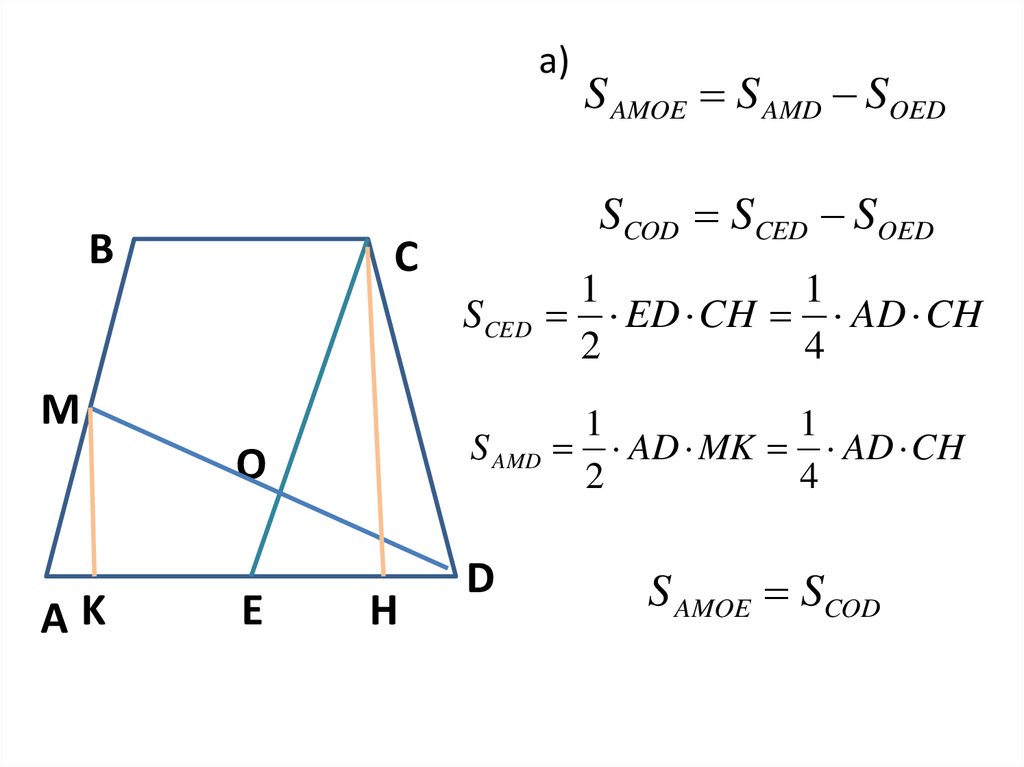
12. Задача №4

В трапеции ABCD точка Е – середина
основания AD, точка М – середина боковой
стороны АВ. Отрезки СЕ и DM пересекаются
в точке О.
а) Докажите, что площади четырехугольника
АМОЕ и треугольника COD равны.
б) Найдите какую часть площадь
четырехугольника АМОЕ составляет от
площади трапеции ABCD, если ВС=3, AD=4.

13.

а)
B
O
AK
SCOD SCED SOED
C
M
E
H
S AMOE S AMD SOED
SCED
1
1
ED CH AD CH
2
4
S AMD
1
1
AD MK AD CH
2
4
D
S AMOE SCOD

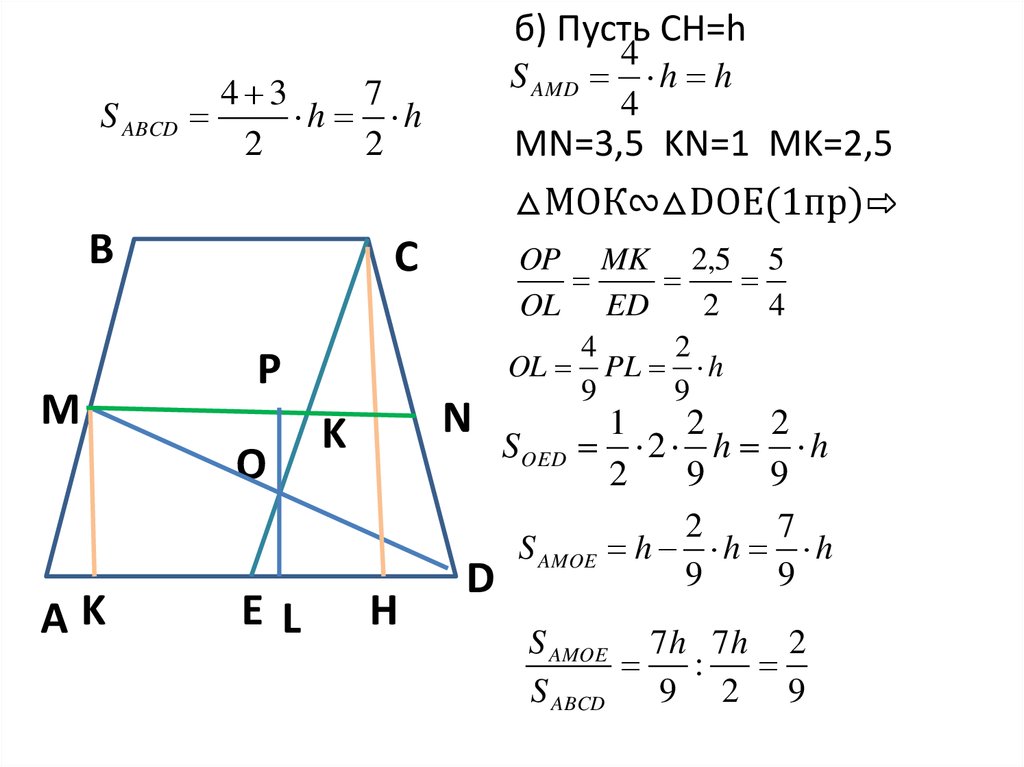
14.

б) Пусть СН=h
S ABCD
B
M
MN=3,5 KN=1 MK=2,5
△МОК∾△DOE(1пр)⇨
C
P
O
AK
S AMD
4 3
7
h h
2
2
EL
N
K
H
4
h h
4
OP MK 2,5 5
OL ED
2
4
4
2
OL PL h
9
9
1
2
2
SOED 2 h h
2
9
9
2
7
S AMOE h h h
9
9
D
S AMOE 7 h 7h 2
:
S ABCD
9 2 9

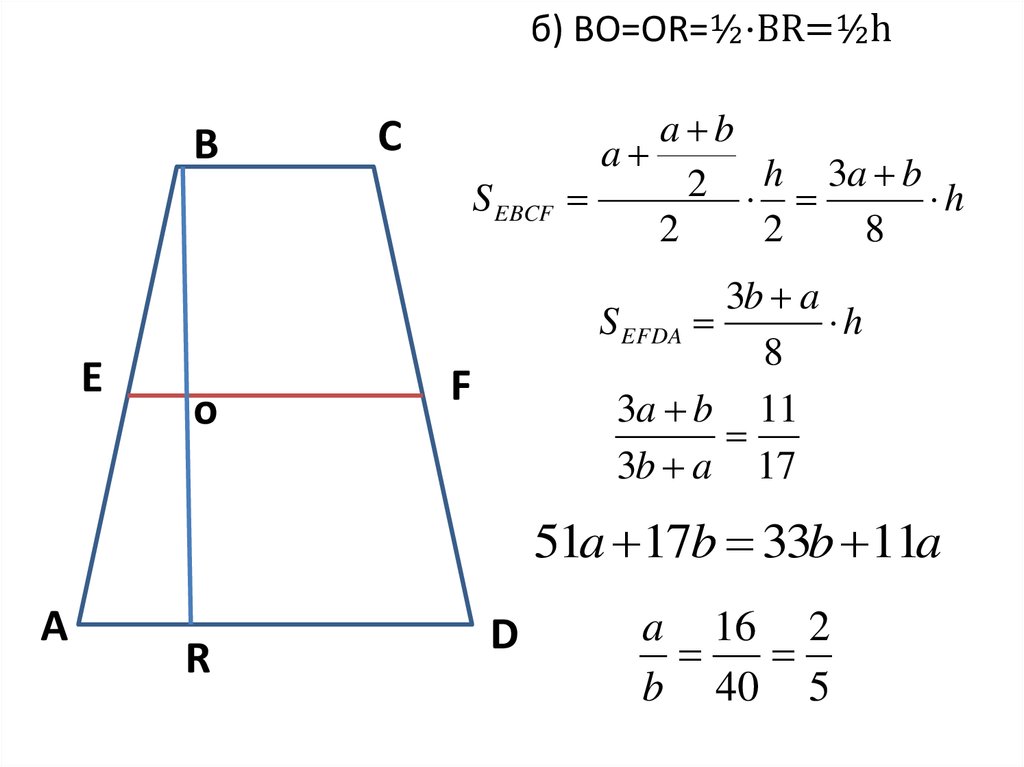
15. Задача № 5

Один из двух отрезков, соединяющих
середины противоположных сторон
четырехугольника делит его площадь
пополам, а другой в отношении 11:17.
а) Докажите, что четырехугольник – трапеция.
б) Найдите отношение оснований трапеции.

16.

а)
K
B
M
C
E
F
A
N
D
S ABMN S MNDC
H △АМD, MN- медиана ⇨
S AMN S MND
S AMB S MCD
Т.к. ВМ=МС и S AMB S MCD
, то DH=AK
Расстояние от точек А и D
до прямой ВС равны, то
AD‖BC
Стороны АВ и СD не
параллельны

17.

б) BO=OR=½⋅BR=½h
B
C
S EBCF
E
o
a b
a
h 3a b
2
h
2
2
8
3b a
S EFDA
h
8
3a b 11
3b a 17
F
51a 17b 33b 11a
A
R
D
a 16 2
b 40 5