Similar presentations:
Геометрические задачи типа 18
1. Геометрические задачи типа 18
МБОУ средняя общеобразовательная школа №9Геометрические задачи типа 18
Газизова. Г.Х., учитель математики МБОУ СОШ №9 г.Бугульма, 2014г.
Презентацию выполнил: Чернобровкин А., ученик 11 класса МБОУ СОШ №9
2. Критерии оценивания выполнения задания С4
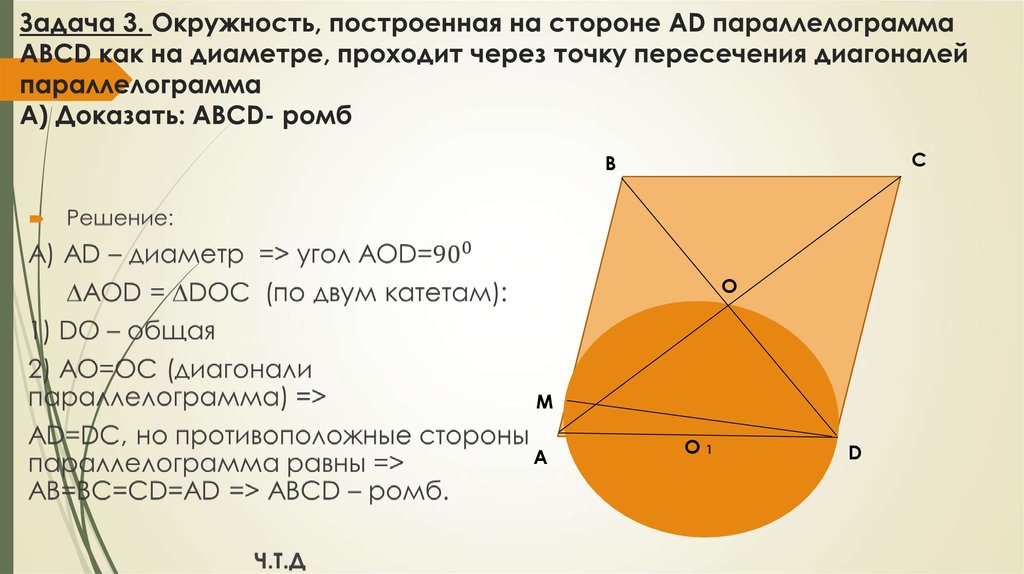
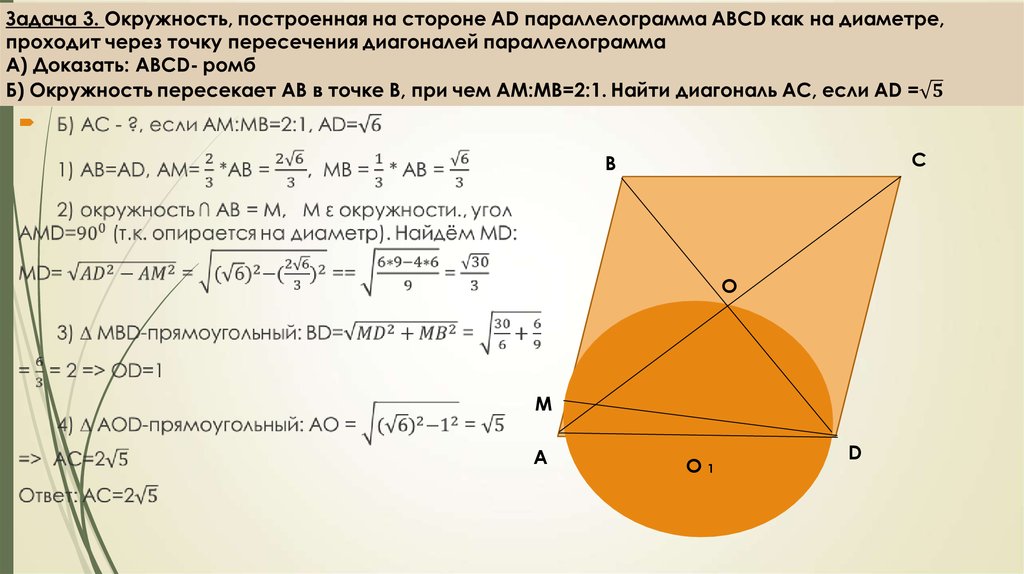
3.
Рекомендации при решении задач по геометрии:внимательно прочитать условие задачи,
построить чертеж, соответствующий условию (по
возможности, наиболее наглядный),
дать характеристику фигуре, вспомнить
определение, свойства, признаки,
определить зависимости между элементами,
рассуждать от вопроса задачи, постепенно
используя данные условия.
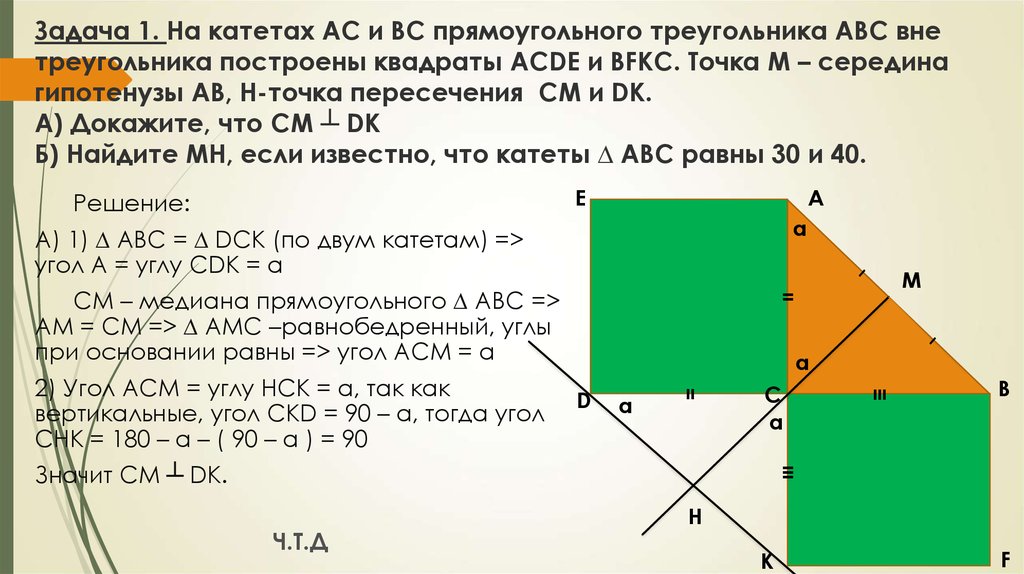
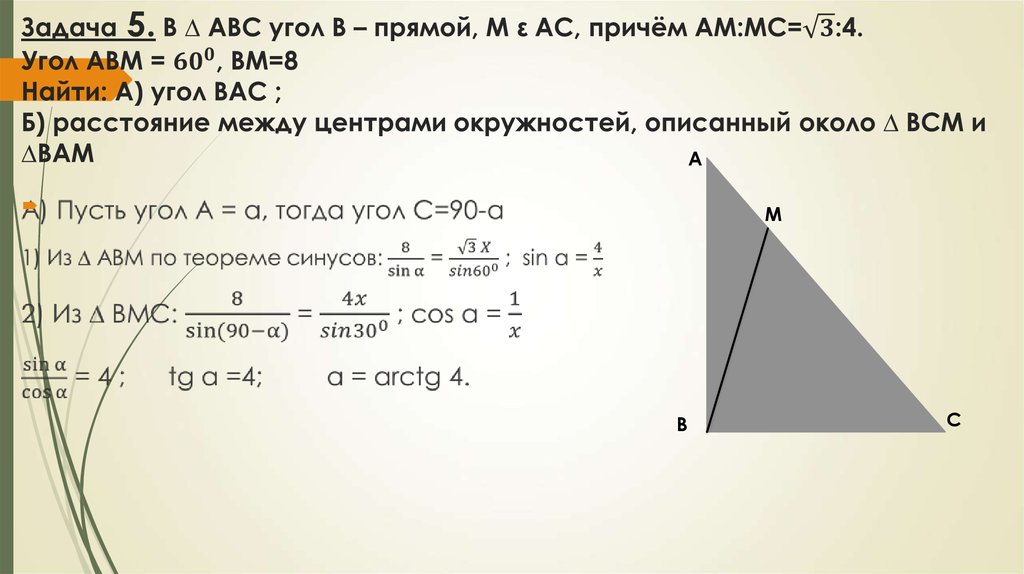
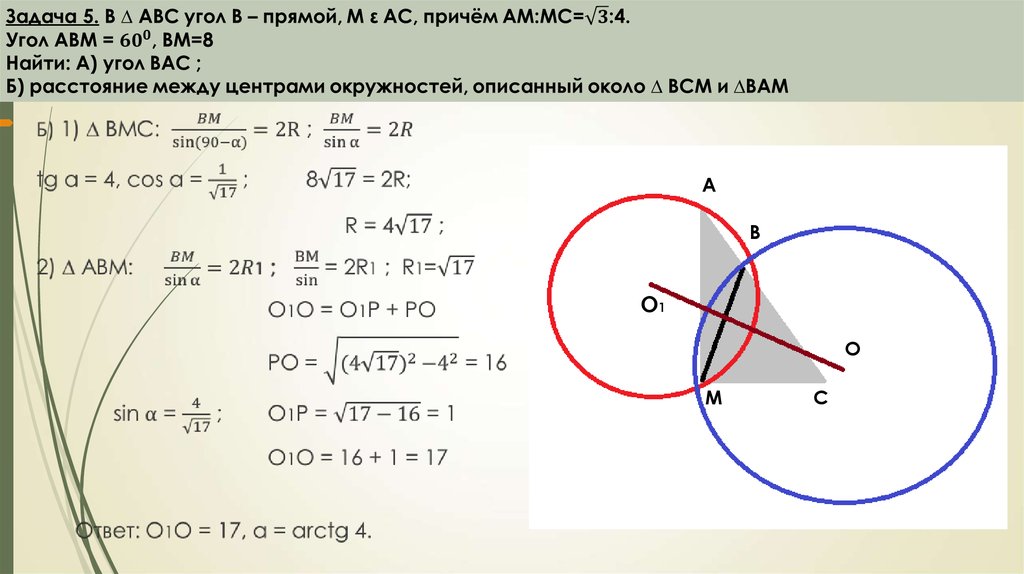
4. Задача 1. На катетах АС и ВС прямоугольного треугольника АВС вне треугольника построены квадраты ACDE и BFKC. Точка М –
серединагипотенузы АВ, H-точка пересечения CM и DK.
А) Докажите, что CM ┴ DK
Б) Найдите MH, если известно, что катеты ∆ АВС равны 30 и 40.
E
Решение:
A
α
А) 1) ∆ ABC = ∆ DCK (по двум катетам) =>
угол А = углу CDK = α
=
CM – медиана прямоугольного ∆ АВС =>
AM = CM => ∆ AMC –равнобедренный, углы
при основании равны => угол ACM = α
α
α
C
α
≡
D
=
2) Угол ACM = углу HCK = α, так как
вертикальные, угол CKD = 90 – α, тогда угол
CHK = 180 – α – ( 90 – α ) = 90
M
B
≡
Значит CM ┴ DK.
Ч.Т.Д
H
K
F
5.
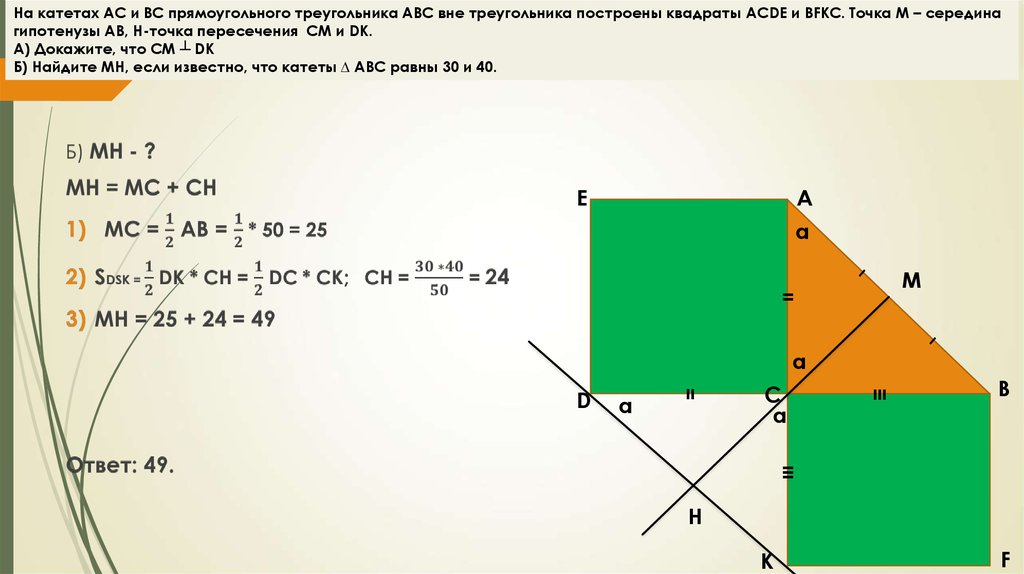
На катетах АС и ВС прямоугольного треугольника АВС вне треугольника построены квадраты ACDE и BFKC. Точка М – серединагипотенузы АВ, H-точка пересечения CM и DK.
А) Докажите, что CM ┴ DK
Б) Найдите MH, если известно, что катеты ∆ АВС равны 30 и 40.
E
A
α
M
=
α
C
α
≡
α
=
D
B
≡
H
K
F
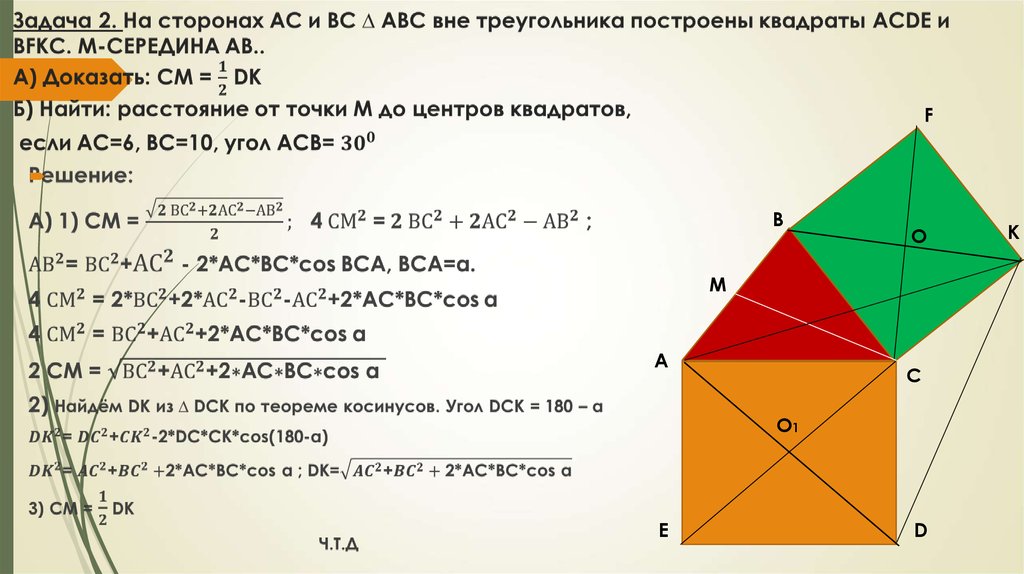
6.
FB
O
M
А
C
O1
E
D
K
7.
FB
O
M
А
C
O1
E
D
K
8.
CB
O
M
А
O1
D
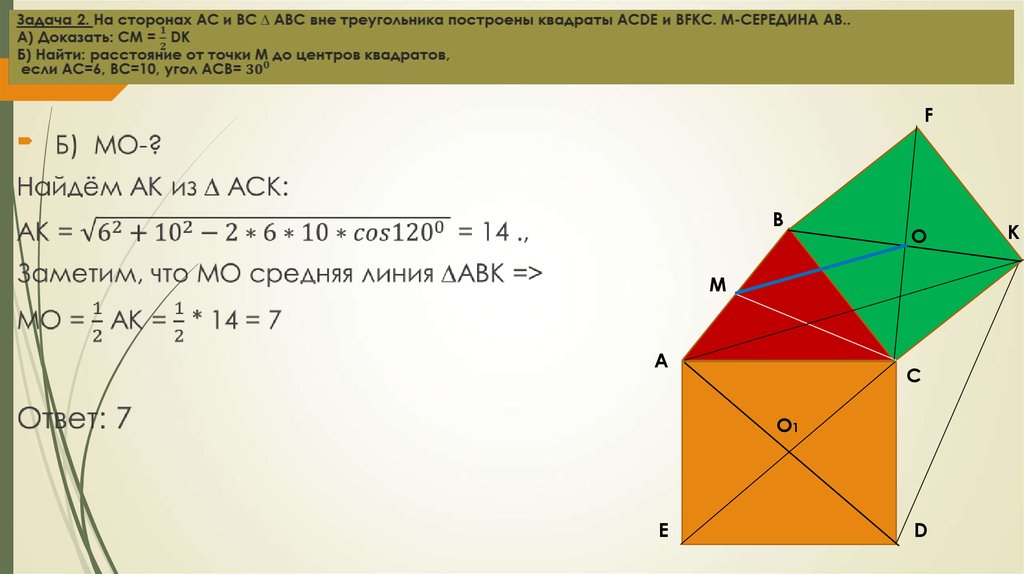
9.
CB
O
M
А
O1
D
10. Задача 4. Через вершины B и C ∆ABC проходит окружность, пересекающая стороны АВ и АС в точках К и М. А) Доказать: ∆АВС ~ ∆AMK
Б) Найти: МК, АМ, если АВ=2, ВС=4, СА=5, АК=1С
B
K
M
A
11.
AM
B
С
12.
АВ
O1
O
М
С
13. Источники:
1. http://alexlarin.net.ru2. ЕГЭ 2014. Математика. Типовые тестовые задания. 30 вариантов
заданий. Под ред. Семенова А.Л., Ященко И.В., М.: Экзамен, 2014
3. ЕГЭ 2014. Математика. Типовые экзаменационные варианты. Под
ред. Семенова А.Л., Ященко И.В., М.: Национальное образование,
2014.





 mathematics
mathematics








