Дисперсионный анализ. Основные задачи дисперсионного анализа

1. ДИСПЕРСИОННЫЙ АНАЛИЗ

2. Основные задачи дисперсионного анализа

Слайд № 1
Основные задачи дисперсионного анализа
Дисперсионный анализ предназначен для проверки наличия
зависимости
нормально
распределенной
результативной
случайной величины Y от нескольких факторов (факторных
величин), а именно для выявления причинно-следственной связи
между вариацией факторов и вариацией результативных
признаков.
Суть дисперсионного анализа состоит в разложении
дисперсии признака на составляющие, обусловленные влиянием
конкретных факторов и проверке гипотез о значимости их влияния.

3. Классификация моделей дисперсионного анализа

Слайд № 2
Классификация моделей дисперсионного анализа
Модели
дисперсионного
следующим образом:
анализа
классифицируются
1) в зависимости от числа факторов на однофакторные,
двухфакторные и т.д.;
2) по природе факторов на детерминированные ( М1 ),
случайные ( М 2 ) и смешанные, в зависимости от того
какими являются уровни факторов.

4. Параметрический однофакторный дисперсионный анализ

Слайд № 3
Постановка задачи
Пусть требуется проверить наличие влияния на результативный
признак одного контролируемого фактора А, имеющего m уровней A j ,
j 1,2,...m . Наблюдаемые значения результативного признака Y на каждом из
фиксированных уровней A j обозначим yij , i 1, n j , где n j - число объектов
наблюдения.
Для изучения случайных величин
рассматриваем априорные
выборки
Реализации априорных выборок представлены в таблице :
Таблица -Реализация априорных выборок
…
…
…
…
…
…
…
…
…

5. Однофакторная модель дисперсионного анализа

Слайд № 4
Однофакторная модель дисперсионного анализа

6.

Априорная модель:
– уровни фактора А фиксированы
– уровни фактора А случайны
Требования к :
(один для всех уровней)

7. Формулировка гипотезы об отсутствии влияния фактора А на результативный признак

Слайд № 5
Формулировка гипотезы об отсутствии влияния
фактора А на результативный признак
В зависимости от изучаемой модели относительно j
предполагается:
модель М 1 – j - фиксированные величины, такие что
j n j 0
H0: j 0 j 1, m , то есть нет влияния фактора А на Y;
модель
М2
–
j
-
случайные
величины,
удовлетворяющие условиям - M j 0 ; M j j ' 0
j j ' ; M j ij 0
дисперсия
i, j ;
M 2j 2
- факторная
H0: 2 0 , то есть нет влияния фактора А на Y.

8. Основные характеристики однофакторного дисперсионного анализа

Слайд № 6
Основные характеристики
однофакторного дисперсионного анализа

9.

10.

Qобщ Qфакт Qост

11. Несмещенные оценки общей, факторной и остаточной дисперсий

12. Проверка гипотезы об отсутствии влияния фактора А на результативный признак

Слайд № 7
Проверка гипотезы об отсутствии влияния фактора
А на результативный признак
2
2
Н0: факт
= ост
.

13. Проверка гипотезы о равенстве двух средних выбранных уровней

Слайд № 8
Проверка гипотезы о равенстве двух средних
выбранных уровней
Если влияние фактора доказано, то можно проверить гипотезы:
H 0 : a j a j
H1 : a j a j
Для проверки нулевой гипотезы строится статистика:
( y* j y* j ' ) 2
F
1
Qост
N m
n jn j'
n j n j'
,
распределенная по закону Фишера-Снедекора
2 N m степенями свободы.
с
1 1
и

14. Проверка гипотезы о значении уровня фактора

Слайд № 9
Проверка гипотезы о значении уровня фактора
При проверке гипотезы H 0 : a a0 используется:
N ( y** a0 ) 2
1
в случае модели M1 статистика: F
, имеющая F
Qост
N m
– распределение с 1 1 и 2 N m степенями свободы;
в случае модели M 2
N ( y** a0 ) 2
1
и n j n статистика: F
,
Qфакт
m 1
имеющая F – распределение с 1 1 и 2 m 1 степенями
свободы.

15. Точечная и интервальная оценка дисперсий

Слайд № 10
Точечная и интервальная оценка дисперсий
Несмещенную точечную оценку для факторной дисперсии
можно уточнить:
N (m 1)
2
2
2
Sˆфакт
( Sˆ факт
Sˆост
) 2
.
2
N nj
уточ
Интервальная оценка для D( ij ) 2 с надежностью
имеет вид:
Qост
Qост
2
.
1
1
x2 (
, N m)
x2 (
, N m)
2
2

16.

НЕПАРАМЕТРИЧЕСКИЙ ОДНОФАКТОРНЫЙ
ДИСПЕРСИОННЫЙ АНАЛИЗ
Критерий
Краскела-Уоллиса
проверяет
однородность
распределения k случайных величин при альтернативной гипотезе
сдвига. Критерий Краскела–Уоллиса
12 k Ri2
H
3(n 1) ,
n(n 1) i 1 ni
k
где n ni , Ri – сумма рангов i-ой выборки, i 1,..., k , при
i 1
справедливости нулевой гипотезы и ni 5 и k 4 имеет
приблизительно распределение «Хи-квадрат» с числом степеней
свободы k 1.
Медианный тест обладает меньшей мощностью и основан на
подсчете числа наблюдений каждой выборки, которые попадают выше
или ниже общей медианы выборок, и вычисляет затем значение
статистики «Хи-квадрат» для таблицы сопряженности 2 k , где k –
число рассматриваемых случайных величин.

17. Двухфакторный дисперсионный анализ

Слайд № 11
Двухфакторный дисперсионный анализ
Постановка задачи
Необходимо исследовать влияние двух факторов А и В на
результативный нормально распределенный признак Y.
Ai , i 1, m ; B j , j 1, l - уровни факторов.
При этом возможны два случая:
1. каждой паре уровней факторов Ai и B j соответствует
одно наблюдаемое значение результативного признака
yij .
2. для каждой пары уровней Ai и B j имеется n(n>1)
наблюдений yijk .

18. Модель двухфакторного дисперсионного анализа (случай I)

виде:
Слайд № 12
Модель двухфакторного дисперсионного анализа
(случай I)
Пусть каждой паре уровней факторов Ai и B j соответствует одно
наблюдаемое значение результативного признака yij , то есть наблюденные
значение можно представить в виде таблицы с двумя входами:
Bj
B1
B2
…
Bl
A1
y11
y12
…
y1l
A2
y21
y22
…
y2l
…
Am
…
ym1
…
ym 2
…
…
…
yml
Ai
Апостериорная модель дисперсионного анализа будем рассматривать в
В этом случае модель дисперсионного анализа будем иметь вид:
yij a i j ij ,
где а – общая генеральная средняя;
ij - независимые нормально распределенные остатки, с M ij 0 и D ij 2 ,
i 1, m ; j 1, l ;
i , j - отклонения от а, обусловленные влиянием соответствующих уровней

19.

Априорная модель:
,
где а – общая генеральная средняя;
ij - независимые нормально распределенные остатки, с M ij 0 и
D ij 2 , i 1, m ; j 1, l ;
i , j - отклонения от а, обусловленные влиянием соответствующих
уровней факторов А и В.
Если уровни факторов Ai и B j фиксированные (модель М1), то i и j
есть неслучайные величины, удовлетворяющие очевидным условиям
m
l
i 1
j 1
i 0 ; j 0 .

20. Формулировка гипотез об отсутствии влияния факторов на результативный признак

Слайд № 13
Формулировка гипотез об отсутствии влияния
факторов на результативный признак
Если уровни факторов Ai и B j фиксированные (модель М 1 ), то i и
j есть неслучайные величины, удовлетворяющие очевидным условиям
m
l
i 1
j 1
i 0 ; j 0 .
Отсутствие
влияния
уровней
факторов
на
изменения
результативного признака - нулевые гипотезы - формулируются в виде:
Н0: i 0 , i 1, m ;
Н0: j 0 , j 1, l .

21.

Продолжение слайда № 13
Если уровни факторов Ai и B j случайные (модель М 2 ), то i и j
считают независимыми между собой и с ij случайными величинами
распределенными нормально с M j M j 0 и D i 2 ; D j 2 .
Н0: 2 0 ;
Н0: 2 0 .
Если уровни фактора А – случайные, а В – фиксированные
(смешанная модель), то i независимые между собой и с ij случайные
величины с
M j 0 ,
удовлетворяющие условию
D i 2 ;
j 0.
j
- неслучайные величины,
Н0: 2 0 ;
Н0: j 0 , j 1, l .
Аналогично строиться смешанная модель, в которой фактор А имеет
фиксированные уровни, а фактор В – случайные.

22. Разложение дисперсии

Слайд № 14
Разложение дисперсии
Qобщ QA QB Qост ,
где
m
QA l ( yi* y** )2 ;
i 1
l
QB m ( y* j y** )2 ;
j 1
m
l
Qост ( yij y* j yi* y** )2
i 1 j 1

23. Проверка гипотезы об отсутствии влияния факторов на результативный признак

Слайд № 15
Проверка гипотезы об отсутствии влияния
факторов на результативный признак
Для проверки нулевой гипотезы об отсутствии влияния
одного из факторов D A; B рассматривается статистика:
QD
m, D A
nD 1
, где n D
F
Qост
l , D B
N nD
распределенная по закону Фишера-Снедекора с 1 n D 1
и 2 N n D степенями свободы.

24. Модель двухфакторного дисперсионного анализа (случай II)

Слайд № 16
Модель двухфакторного дисперсионного анализа
(случай II)
В общем случае, когда для каждой пары уровней Ai и
B j имеется n(n>1) наблюдений, модель дисперсионного
анализа представляется в виде:
yijk a i j ( ) ij ijk ,
i 1, m , j 1, l , k 1, n ,
где yijk - к-ое наблюдение результативного признака для iго уровня фактора А и j-го уровня фактора В;
а – общая генеральная средняя;
i , j - отклонения от а, обусловленные влиянием
соответствующих уровней Аi и Вj;
( ) ij - отклонения от а, обусловленные совместным
влиянием уровней факторов А и В;
ijk (0, ) и независимы между собой.

25. Формулировка гипотез об отсутствии влияния факторов на результативный признак

Слайд № 17
Формулировка гипотез об отсутствии влияния
факторов на результативный признак
Если уровни факторов Аi и Вj фиксированные (модель
М 1 ), то отклонения i , j и ( ) ij - неслучайные
величины,
удовлетворяющие
условиям:
m
l
m
l
i 1
j 1
i 1
j 1
i 0 ; j 0 ; ( )ij 0 ; ( )ij 0 .
Нулевые гипотезы об отсутствии влияния:
фактора А – Н0: i 0 ; i 1, m ;
фактора В – Н0: j 0 ; j 1, l ;
совместного
влияния
факторов
А
и
Н0: ( ) ij 0 ; i 1, m ; j 1, l .
В
–

26.

Продолжение слайда № 17
В случае модели М 2 i , j и ( ) ij есть независимые
между собой и с ijk случайные величины, распределенные
нормально с нулевым математическим ожиданием и с
2
дисперсиями 2 , 2 и
.
Нулевые гипотезы от отсутствии влияния:
фактора А – Н0: 2 0 ;
фактора В – Н0: 2 0 ;
2
совместного влияния факторов А и В – Н0:
0.

27.

Продолжение слайда № 17
Для смешанной модели, когда, к примеру, уровни фактора А
случайные, а фактора В – фиксированные, отклонения i и ( ) ij
независимые между собой и с ijk нормально распределены случайные
величины с нулевыми математическими ожиданиями, с дисперсиями
2
2
и , при этом
m
l
l
i 1
j 1
j 1
( )ij 0 , а ( )ij 0 ; j 0 .
Нулевые гипотезы об отсутствии влияния факторов имеют вид:
фактора А – Н0: 2 0 ;
фактора В – Н0: j 0 ; j 1, l ;
2
совместного влияния факторов А и В – Н0:
0 .`
Аналогично строится другая смешанная модель.

28. Разложение дисперсии

Слайд № 18
Разложение дисперсии
Qобщ Q A Q B Q AB Qост ,
где
Qобщ ( y ijk y ***) ;
m
l
n
2
i 1 j 1 k 1
m
QA l n ( y
i 1
i** y ***)
2
;
QB m n ( y * j* y***) ;
l
2
j 1
m
l
QAB n ( y
i 1 j 1
ij*
y
i**
y* j* y***)
Qост ( y ijk y ij*) .
m
l
n
i 1 j 1 k 1
2
2
;

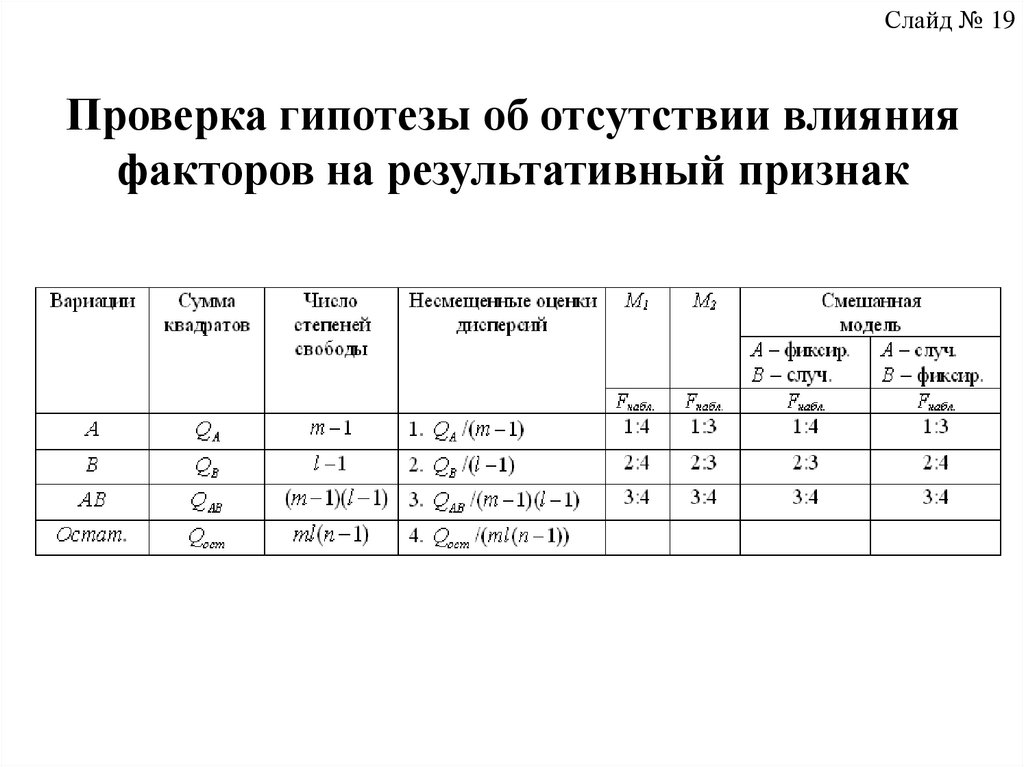
29. Проверка гипотезы об отсутствии влияния факторов на результативный признак

Слайд № 19
Проверка гипотезы об отсутствии влияния
факторов на результативный признак

30.

НЕПАРАМЕТРИЧЕСКИЙ ДВУХФАКТОРНЫЙ
ДИСПЕРСИОННЫЙ АНАЛИЗ
Для проверки однородности распределения
k 2 зависимых совокупностей следует использовать
непараметрические альтернативы двухфакторного
дисперсионного
анализа,
например,
критерий
Фридмана:
2
12
Rij 3k (n 1) ,
F
kn(n 1) i 1 j 1
n
k
где Rij – ранг i-го объекта по j-му признаку.
Критерий Фридмана при справедливости нулевой
гипотезы аппроксимируется распределением «Хиквадрат» с числом степеней свободы n-1.