Similar presentations:
Основы дисперсионного анализа. Однофакторный дисперсионный анализ
1. Основы дисперсионного анализа. Однофакторный дисперсионный анализ.
Лекция 42. Дисперсионный анализ позволяет оценить
значимость и долю влияния отдельныхфакторов и их взаимодействия на
вариацию того или иного признака;
достоверность различий между средними
по градациям факторов.
3. Общие теоретические предпосылки анализа.
Пример 1. На урожайность растений влияет факторА (доза внесения удобрений), тогда
xi x A e
где
А – доля отклонений переменной, связанная с
влиянием данного фактора;
е – остаточная часть отклонения (результат
2
2
2
случайных отклонений).
y
A e
Если выразить в дисперсиях
4. Продолжение. Общие теоретические предпосылки анализа.
Общие теоретическиепредпосылки анализа.
Продолжение.
Пример 2. На признак (урожайность) оказывают
влияние 2 фактора А (доза внесения удобрений) и В
(площадь питания растений).
Тогда:
xi x A B AB e
где А (В) – доля отклонения, связанная с влиянием
фактора А (В);
АВ – доля отклонения, связанная со взаимодействием
двух факторов;
е – случайная часть отклонения.
2
2
2
2
2
В дисперсиях:
y
A
B
AB
e
5. Продолжение. Общие теоретические предпосылки анализа.
Общие теоретическиепредпосылки анализа.
Продолжение.
Пример 3. На признак (урожайность)
оказывают влияние 3 фактора А (доза
внесения удобрений), В (площадь питания
растений) и С (полив).
В дисперсиях:
2
y
2
A
2
B
2
C
2
AB
2
BC
2
AC
2
ABC
2
e
6. Градации факторов
1)2)
Градации фактора – это несколько
состояний или уровней одного фактора.
Типы градаций:
фиксированные, например, год
наблюдения, месяц, район
возделывания, сорт и т.д.;
случайные, например, число растений в
семье и т.п.
7. Схемы дисперсионного анализа.
1) по числу факторов;2) по типу градаций факторов;
3) по сочетанию градаций разных факторов – полные
(градации одного фактора сочетаются с каждой
градацией другого фактора) и иерархические
(градации одного фактора связаны с градациями
другого фактора по иерархической схеме);
4) по числу наблюдений по каждой градации фактора
– равномерные (число наблюдений одинаковое) и
неравномерные (число наблюдений неодинаковое).
8. Ограничения при проведении дисперсионного анализа:
1) число градаций по фактору должно бытьне менее двух;
2) число наблюдений по сочетанию градаций
разных факторов должно быть не менее
двух;
3) дисперсии по градациям факторам
должны быть примерно одинаковыми;
4) распределение величин по градациям
факторов должно соответствовать
нормальному распределению.
9. Нулевая гипотеза (Но)
Но - вся вариация признака являетсятолько случайной и не зависит от
влияния тех или иных факторов.
На – на изменчивость признака влияет тот
или иной фактор или взаимодействие этих
факторов.
10. Общие этапы дисперсионного анализа
1) вычисление сумм квадратов отклонений(SS);
2) вычисление чисел степеней свободы (df);
3) вычисление средних квадратов (ms);
4) вычисление критерия Фишера (F);
5) определение критических значений
критерия Фишера (F05 и F01);
11. продолжение. Общие этапы дисперсионного анализа
6) определение достоверности влияния факторов;7) вычисление дисперсий (σ2);
8) вычисление долей влияния факторов (pin);
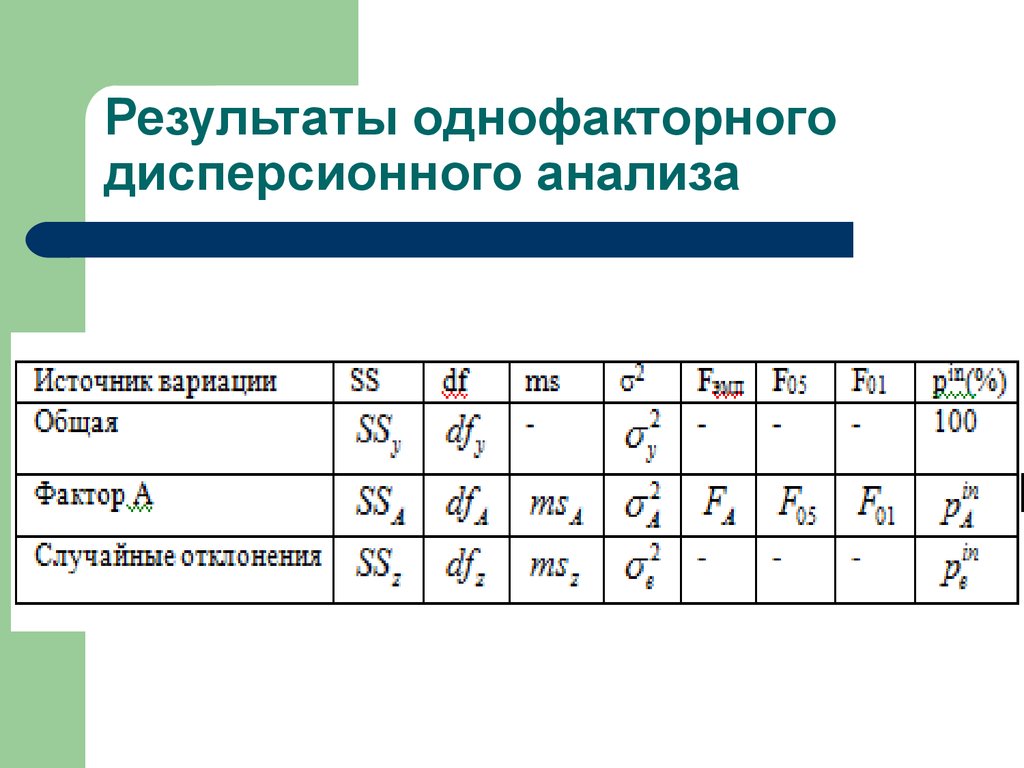
9) построение таблицы результатов дисперсионного
анализа;
10) вычисление наименьшей существенной разности
(НСР) между средними;
11) сравнение групповых средних.
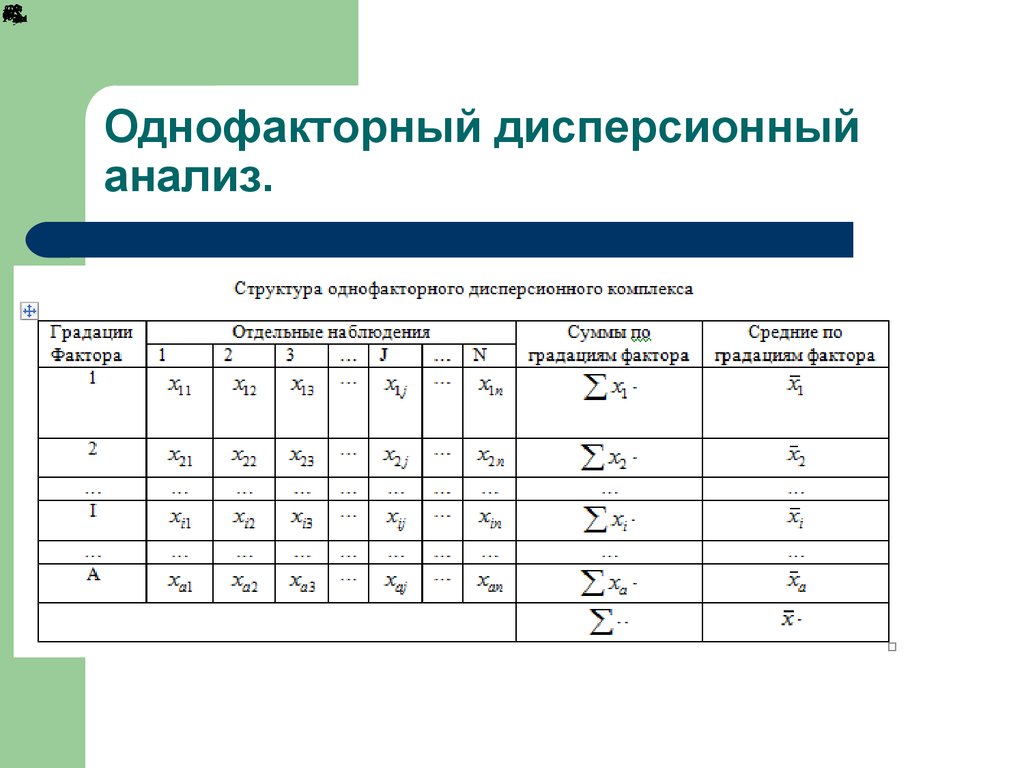
12. Однофакторный дисперсионный анализ.
in2
df
SS
F
ms
p01
y
05
A
zyzA
eyAA
Однофакторный дисперсионный
анализ.
13. Суммы квадратов отклонений вариант от средних.
SS y ( xij x ) 2 xij2x
N
ij
SS A ni ( xi x ) 2
i
2
x
x
2
i
i
ni
N
xi
2
2
SS z ( xij xi ) xij
ni
i j
i
Проверочное действие
2
2
SS y SS A SS z
14. Степени свободы
df y N 1df A a 1
df z N a
Проверочное действие
df y df A df z
15. Средние квадраты
Факториальный средний квадратSS A
(msA) характеризует варьирование
средних по градациям фактора вокруг ms A
df A
средней по комплексу, то есть,
оценивает влияние изучаемого
фактора.
Остаточный средний квадрат (msz)
характеризует варьирование
отдельных наблюдений вокруг средних
SS z
по градациям фактора, то есть,
msz
случайную вариацию. Данный средний
df z
квадрат является мерой случайной
ошибки в дисперсионном комплексе.
16. Критерии Фишера
1)ms A
FA
msz
2) По таблицам критических значений критерия находят
F05 и F01 на пересечении df1 и df2 .
df1 – столбцы таблицы, которые соответствуют числу
степеней свободы по фактору (dfA)
df2 – сроки таблицы, соответствующие числу степеней
свободы случайной вариации (dfz), на их пересечении
и находится искомое значение критерия Фишера.
17. Критерии Фишера
Если FA>F05 и FA>F01, нулевая гипотезаотвергается.
Если F05<FA<F01 , то на уровне значимости 05
нулевую гипотезу следует отвергнуть, а на уровне
значимости 01 – следует принять. В этом случае
разумней продолжить экспериментальные
исследования влияния данного фактора.
Если FA<F05 , то нулевая гипотеза об отсутствии
влияния фактора принимается. И на этом
дисперсионный анализ завершается.
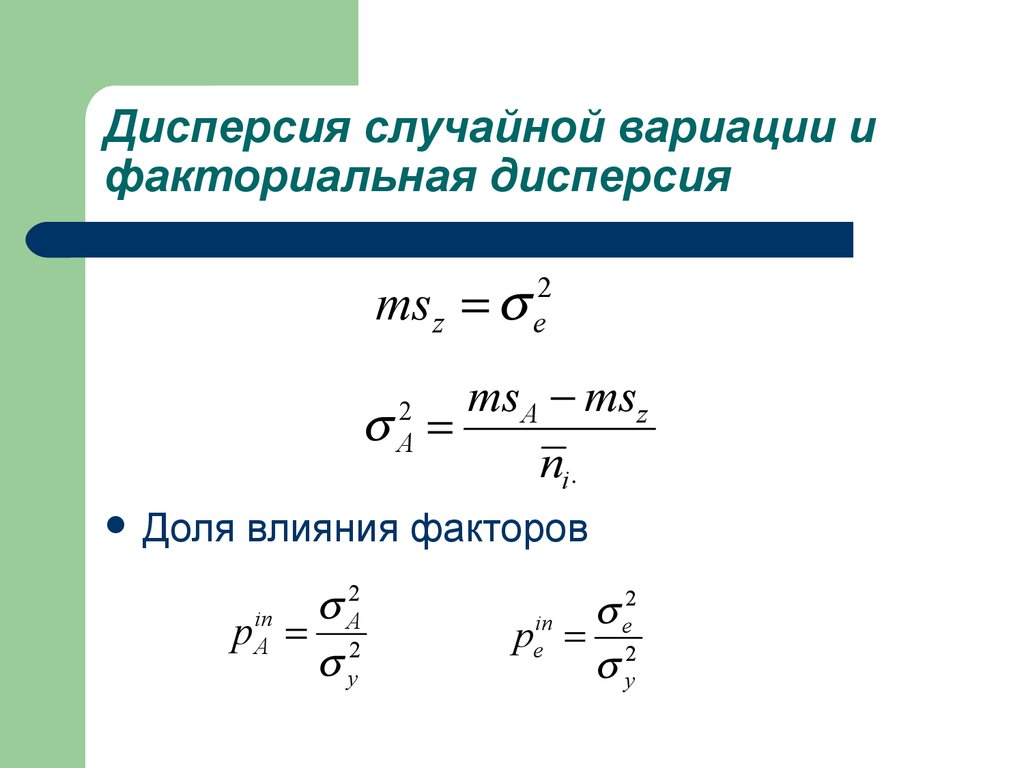
18. Дисперсия случайной вариации и факториальная дисперсия
msz2
e
ms A msz
ni
2
A
Доля влияния факторов
2
p inA A2
y
2
pein e2
y
















 mathematics
mathematics