Основы дисперсионного анализа

1. ОСНОВЫ ДИСПЕРСИОННОГО АНАЛИЗА

Лекция №9
для студентов 2 курса,
обучающихся по специальности 060609 –
Медицинская кибернетика
доц. Шапиро Л.А.
Красноярск, 2015 г.

2. План лекции:

• Актуальность темы.
• Виды дисперсионного анализа и его
характеристики
• Этапы дисперсионного анализа
• Формулы для однофакторного
дисперсионного анализа
• Сила влияния фактора
• Множественные сравнения.

3. Актуальность темы

Основной целью дисперсионного
анализа является исследование
значимости различия между
средними при числе сравниваемых
выборок больше двух

4.

Нулевая гипотеза:
В генеральной совокупности групповые средние
нормальных совокупностей с одинаковыми
дисперсиями равны между собой
x1 x2 ... xn
Для проверки этой нулевой гипотезы достаточно
проверить по критерию Фишера нулевую гипотезу о
равенстве факторной и случайной дисперсии
(в этом состоит метод ДА)

5. Условия:

• изучаемые факторы должны быть независимыми;
• распределение
выборочных
данных
должно
соответствовать нормальному распределению или
сводится
к
нему
путем
соответствующих
преобразований
• Выборки однородны - выборочные дисперсии не
различаются значимо (критерии Кочрена, Левене,
Бартлета и т.д.)
х – =А+е, где – средняя арифметическая
генеральной совокупности;
х – конкретное значение переменной;
А – доля отклонения переменной, связанная с влиянием
данного конкретного фактора;
е – остаточная часть отклонения, не объяснимая
влиянием данного фактора.

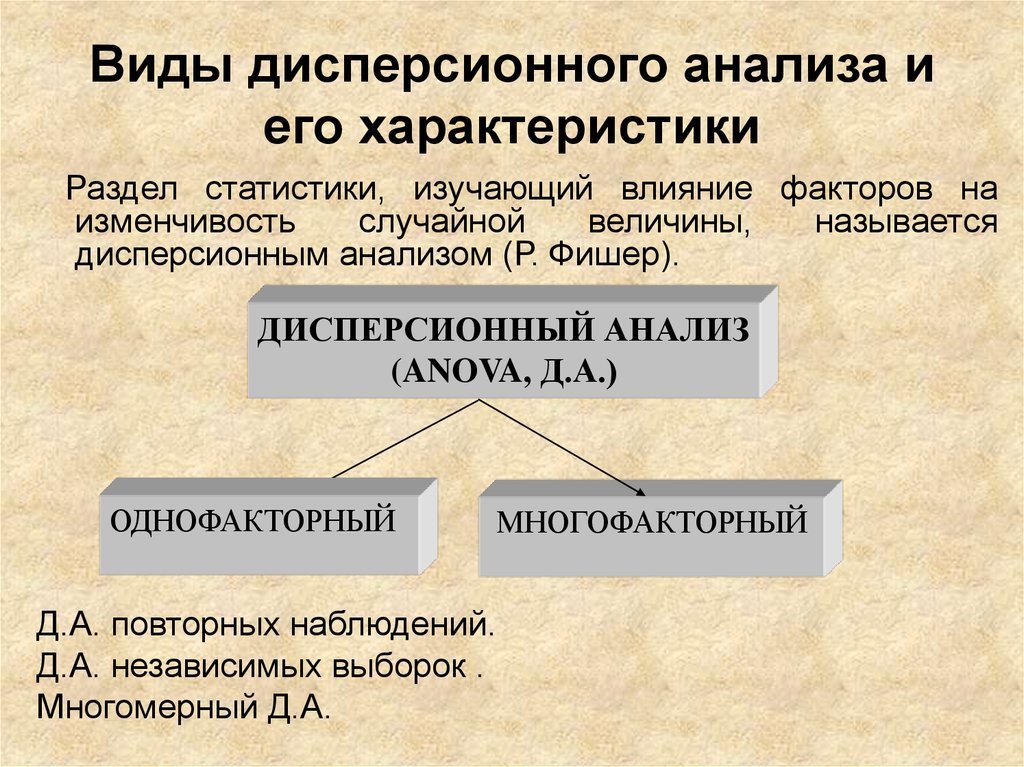
6. Виды дисперсионного анализа и его характеристики

Раздел статистики, изучающий влияние факторов на
изменчивость
случайной
величины,
называется
дисперсионным анализом (Р. Фишер).
ДИСПЕРСИОННЫЙ АНАЛИЗ
(ANOVA, Д.А.)
ОДНОФАКТОРНЫЙ
МНОГОФАКТОРНЫЙ
Д.А. повторных наблюдений.
Д.А. независимых выборок .
Многомерный Д.А.

7.

• Признаки, изменяющиеся под влиянием тех
или иных причин, называются результативными
(зависимыми).
• Сами
причины
называются
факторами
(независимые переменные).
• Конкретное значение фактора называется
градацией (или уровнем) фактора (доза
препарата, степень тяжести заболевания).
• Градациям
(уровням)
межгруппового
фактора соответствуют независимые выборки
объектов.
• Градациям
(уровням)
внутригруппового
фактора соответствуют зависимые выборки
объектов (повторные измерения).

8.

При однофакторном ANOVA изучается влияние одного
фактора на зависимую переменную. Проверяется одна
гипотеза.
Многофакторный ANOVA позволяет проверять гипотезы не
только о влиянии каждого фактора в отдельности, но и о
взаимодействии факторов.
Пример: двухфакторный ANOVA. Изучается влияние двух
факторов А-степень тяжести заболевания, B – пол на
содержание гемоглобина. Проверяется три гипотезы:
1. Влияние степени тяжести заболевания (А).
2. Влияние гендерных различий (В).
3. Взаимодействие факторов АВ (зависимость степени
влияния одного фактора от градаций другого).

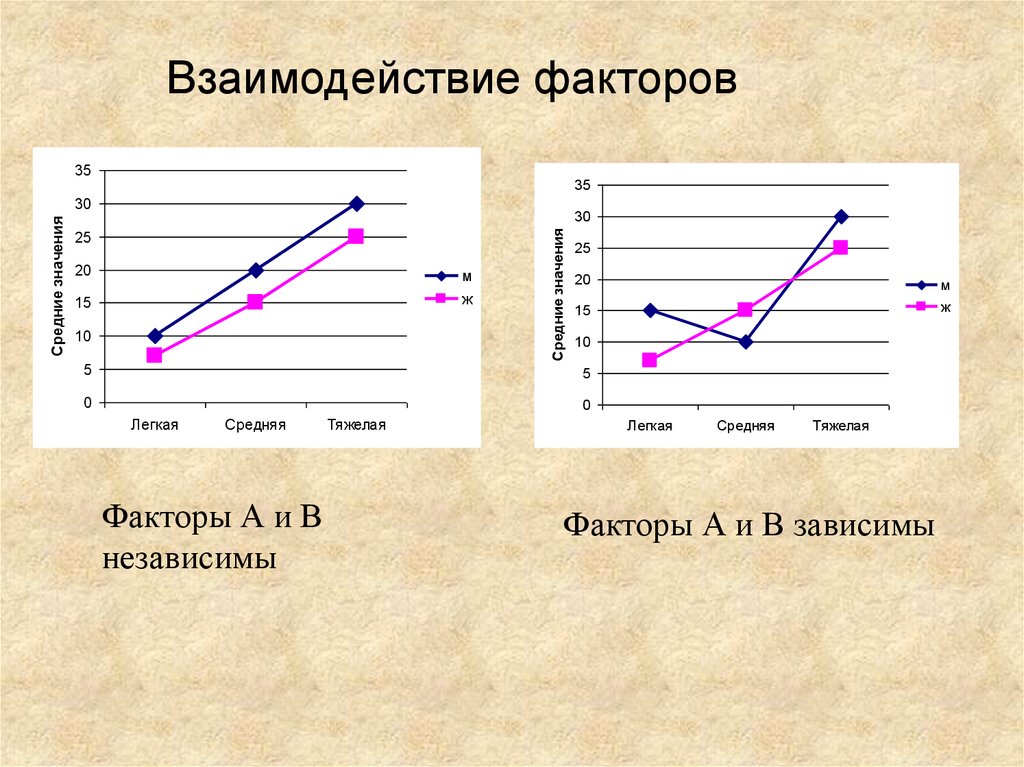
9.

Взаимодействие факторов
35
35
30
25
20
м
ж
15
10
5
Средние значения
Средние значения
30
25
20
м
ж
15
10
5
0
0
Легкая
Средняя
Факторы А и В
независимы
Тяжелая
Легкая
Средняя
Тяжелая
Факторы А и В зависимы

10.

Пример: трехфакторный ANOVA. Факторы А, В, С.
Проверяется семь гипотез:
1. А
2. В
3.С
4. АВ
5. АС
6. ВС 7. АВС
Двухфакторный ANOVA с повторными измерениями по одному
из факторов проверяются три гипотезы:
1. Влияние внутригруппового фактора.
2. Влияние межгруппового фактора.
3. Взаимодействие внутригруппового и межгруппового
фактора.
Степень изменения всех признаков и отклонение их от
средней арифметической ряда характеризуется дисперсией
D(х):
n
D( x ) s
2
2
(
x
x
)
i
i 1
n 1
D(X)=M(X2)-(M(X))2

11.

Однофакторный дисперсионный анализ.
Идея метода - разложить показатель изменчивости
признака на две составляющие: изменчивость между
группами и изменчивость внутри групп.
Dобщ = Dфакт + Dслуч
F
Dфакт
Dслуч
- критерий Фишера
Если F>Fкр (при уровне значимости =0,05), то
влияние фактора существенно.
Если F<Fкр (уровень значимости > 0,05),
фактор не влияет на изучаемый признак.

12. Этапы дисперсионного анализа:

• Представить данные в виде таблицы.
Номер
наблюдения
(j)
1
2
...
j
n
Средние по
группам:
Уровни фактора(i)
3
...
a
1
2
x11
x21
x31
xa1
x12
x22
x32
xa2
x1j
x2j
x3j
xaj
x1n
x2n
x3n
xan
x1
x2
x3
xa
i – индекс уровня фактора (от 1 до а);
j – индекс варианты (от 1 до n).

13.

• Общее варьирование всех вариант (хij),
независимо от того, в какой группе они находятся,
вокруг общей средней x характеризуется
дисперсией Dобщ.
Dобщ
( x ij x )
2
ij
N 1
где N=a∙n– число всех вариант;
dfобщ.= N–1 – число степеней свободы.

14.

• Варьирование групповых средних x i или средних
каждого уровня данного изучаемого фактора вокруг
общей средней x , характеризуется факторной
дисперсией Dфакт.
Dфакт
ni( x i x )
2
i
a 1
dfфакт= a – 1– число степеней свободы.
ni – среднее число вариант в каждой группе,
n – если число вариант в группах одинаково.

15.

• Варьирование вариант хij внутри каждой
группы вокруг каждой групповой средней x i
характеризует случайная или остаточная
дисперсия Dслуч.
2
( xij xi)
i j
Dслуч
N a
df случ =N - a – число степеней свободы.
Причем: (N – a) + (a – 1) = N – 1

16. Формулы для однофакторного дисперсионного анализа

Источник
варьирования
Сумма
Число
квадратов SS степеней
(числитель) свободы df
(знаменатель)
Общее
(все
варианты)
2
(
x
x
)
ij
Групповые
средние
(фактор А)
n i (x i x) 2
ij
N–1
a –1
i
Варианты
2
(
x
x
)
ij i
внутри групп
i j
(случайные
отклонения)
N–a
Формулы для
дисперсии
MS
1
N 1
1
a 1
2
(
x
x
)
ij
ij
2
n
(
x
x
)
i i
i
1
2
(
x
x
)
ij i
N a i j

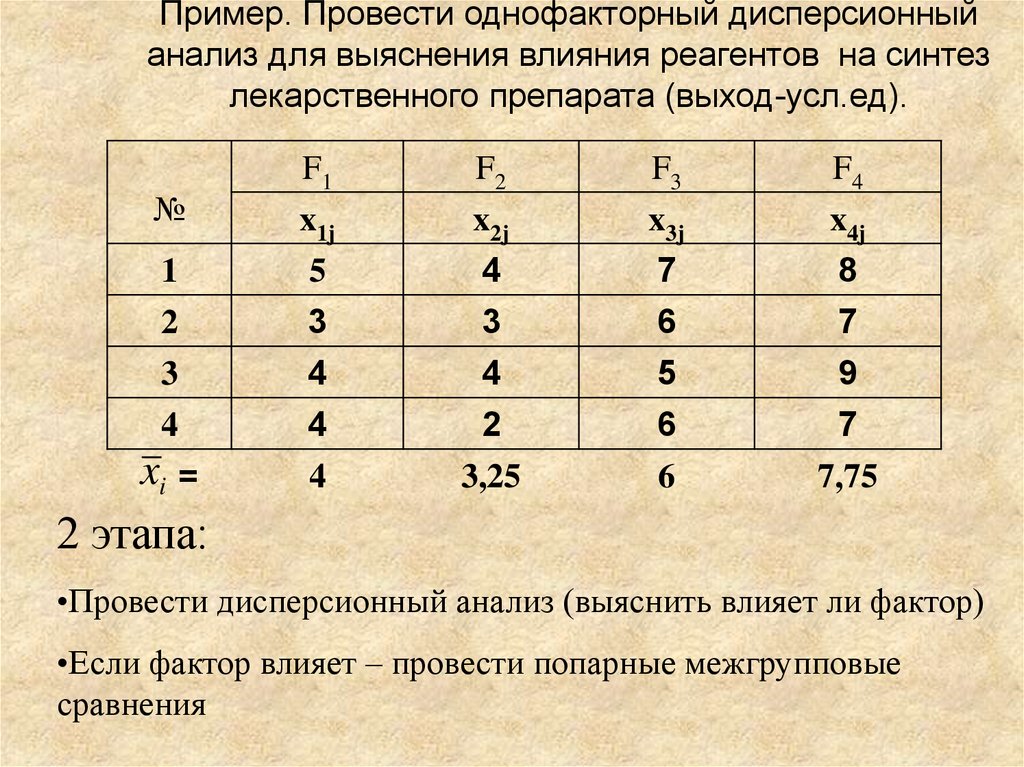
17. Пример. Провести однофакторный дисперсионный анализ для выяснения влияния реагентов на синтез лекарственного препарата (выход-усл.ед).

№
1
2
3
4
xi =
F1
x1j
5
3
4
4
4
F2
x2j
F3
x3j
F4
x4j
4
3
4
2
3,25
7
6
5
6
6
8
7
9
7
7,75
2 этапа:
•Провести дисперсионный анализ (выяснить влияет ли фактор)
•Если фактор влияет – провести попарные межгрупповые
сравнения

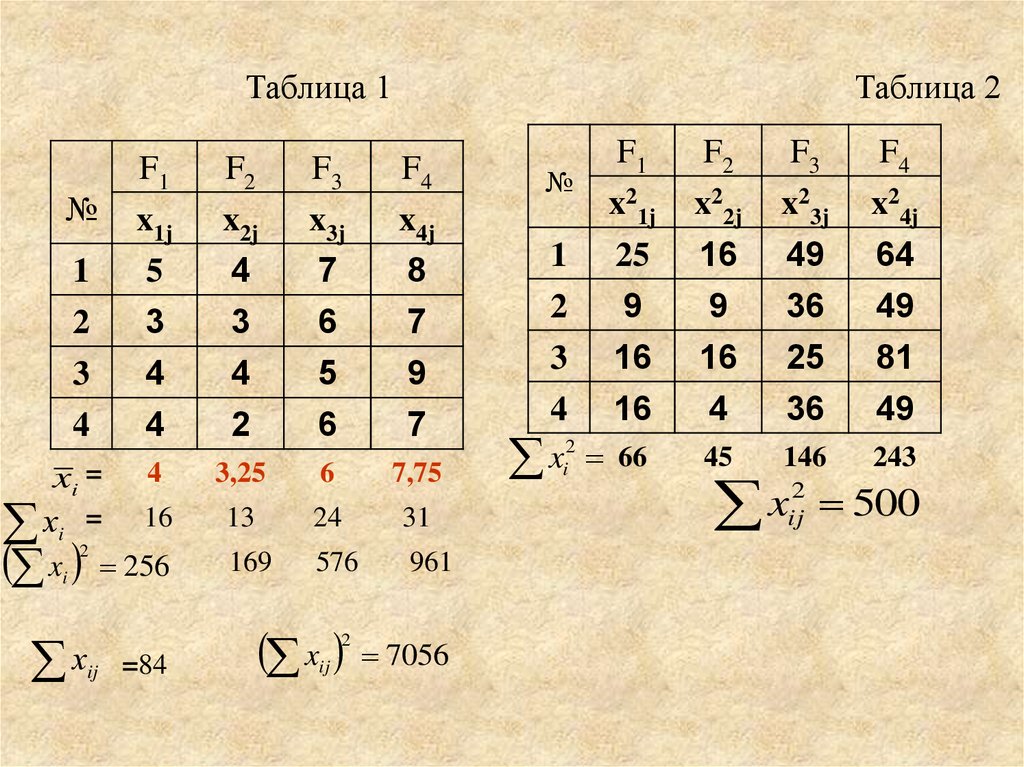
18.

Таблица 1
№
1
2
3
4
xi =
F1
x1j
5
F2
x2j
F3
x3j
F4
x4j
3
4
4
4
3
4
2
7
6
5
6
8
7
9
7
4
3,25
6
7,75
13
24
31
169
576
961
х = 16
x 256
i
2
i
х
ij
Таблица 2
x
2
=84
ij
7056
№
F1
x21j
F2
x22j
F3
x23j
F4
x24j
25
49
36
25
64
49
81
1
2
3
9
16
16
9
16
4
16
4
36
49
45
146
243
2
x
i 66
2
x
ij 500

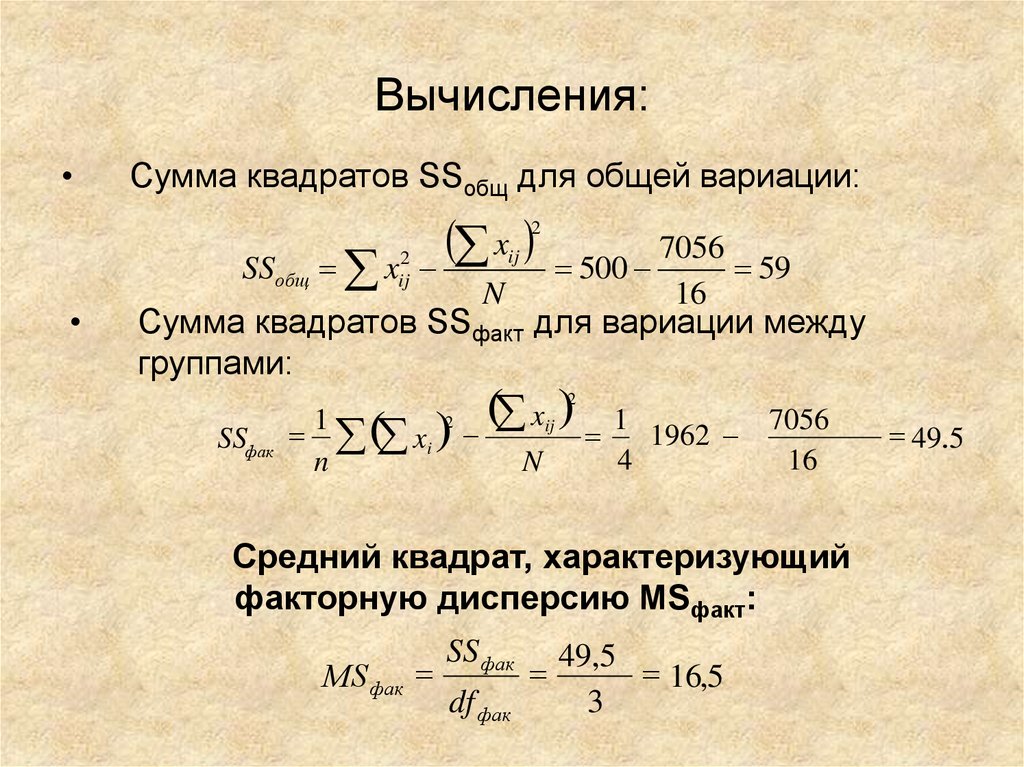
19. Вычисления:

Сумма квадратов SSобщ для общей вариации:
x
x
N
2
SSобщ
7056
500
59
16
ij
2
ij
Сумма квадратов SSфакт для вариации между
группами:
x 1
1
x
2
SSфак
2
n
i
ij
N
4
1962
7056
16
Средний квадрат, характеризующий
факторную дисперсию MSфакт:
МS фак
SS фак
df фак
49.5
,
16,5
3
49.5
.

20.

Сумма квадратов SSсл для вариации
внутри групп:
SSсл=SSобщ – SSфак = 59 – 49,5=9,5
Средний квадрат MSсл для вариации
внутри групп:
SSсл 9,5
MS сл
0,79
df сл 12
т.к MSсл< MSфак,
F
MSфак
MSсл
16,5
20,84
0,79
а Fкрит=3,49 для =0,05 и dfсл=12 и dfфак=3
ВЛИЯНИЕ ФАКТОРА ДОСТОВЕРНО!

21. Сила влияния фактора

• Сила влияния фактора A определяется:
2
2
А
Dфакт .
где
Dфакт . Dсл уч.
MSфакт . MSслуч. MSфакт . Dслуч.
Dфакт
n
n
В нашем случае
Dфакт.
Dфакт. Dслуч .
2
А
Dфакт
16,5 0,79
3,93
4
3, 93
3, 93 0 , 79
0,83 83%

22.

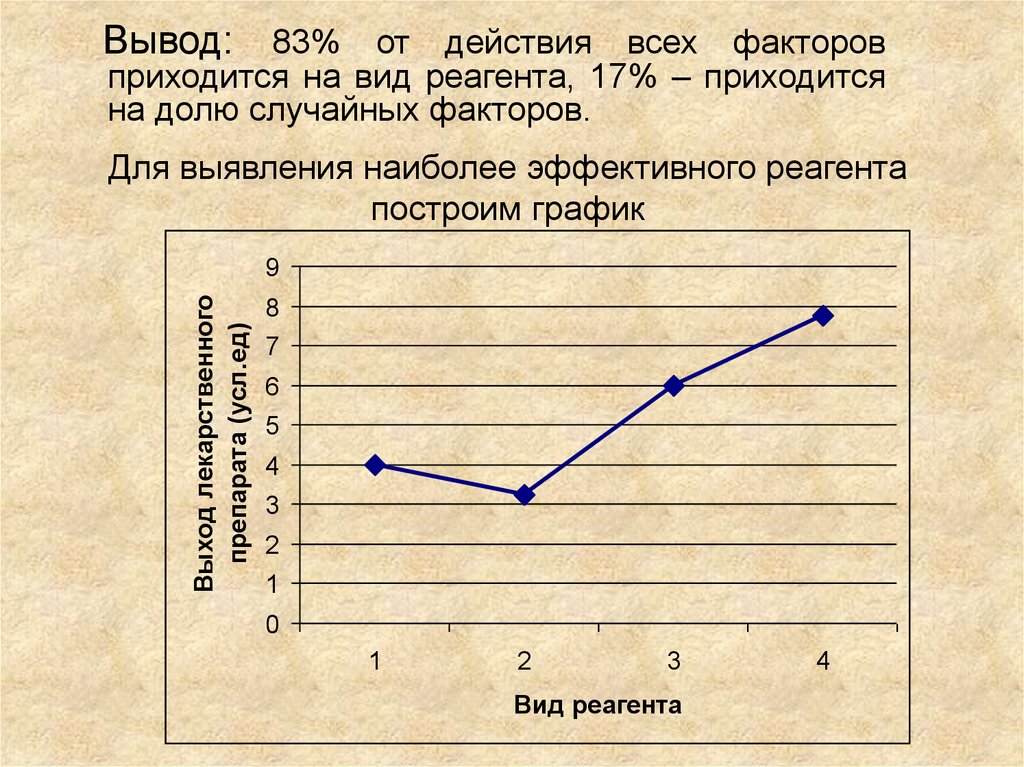
Вывод: 83% от действия всех факторов
приходится на вид реагента, 17% – приходится
на долю случайных факторов.
Для выявления наиболее эффективного реагента
построим график
Выход лекарственного
препарата (усл.ед)
9
8
7
6
5
4
3
2
1
0
1
2
3
Вид реагента
4

23. Множественные сравнения

• Дисперсионный анализ позволяет установить,
существуют ли достоверные различия между
отдельными уровнями фактора (средними
арифметическими отдельных групп).
• Между какими группами конкретно имеется
разница - необходимо выяснить.
n – число вариант в каждой группе.
Sd
Dслуч.
n
d
t
Sd
• Отношение разницы d к ее ошибке Sd , т.е.
должно
быть таким, чтобы оно гарантировало значимость не
менее чем при =0,05.

24.

• Коэффициент Q, рассчитан для разного
количества групп а и степеней свободы dfслуч.
Sd
Dслуч.
n
0,79
0,2
4
d12=4-3,25=0,7;
d12 0,7
t12
3,8;
S d 0,2
d23=6-3,25=2,75;
d 23 2,75
t 23
13,9;
Sd
0,2
Q=4,2 для dfслуч=12 и а=4;
t12< Q, разница не достоверна
t23> Q, разница достоверна

25. Вывод:

Вид реагента достоверно влияет на
выход лекарственного препарата.
Наибольшую эффективность имеет
фактор (реагент), градация которого
равна F4.

26. Множественные сравнения

• Поправка Бонферрони
если имеется n групп, то уровень значимости
0,05
n
например, при n=3 =0,05/3=0,017
Критерии:
LSD (наименьшей значимой разности)
Ньюмена-Кейлса
Шеффе
Тьюки и т.д.

27. Заключение

Таким образом, нами рассмотрены
основы дисперсионного анализа,
изучающего влияние факторов на
изменчивость случайной величины

28. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:

Основная литература:
Попов А.М. Теория вероятней и
математическая статистика /А.М. Попов, В.Н.
Сотников. – М.: ЮРАЙТ, 2011. – 440 с.
Герасимов А. Н. Медицинская статистика:
учебное пособие / А. Н. Герасимов. – М. : Мед.
информ. агентство, 2007. – 480 с.
Балдин К. В. Основы теории вероятностей и
математической статистики : учебник / К. В.
Балдин. – М. : Флинта, 2010. – 488с.
Учебно–методические пособия:
Шапиро Л.А., Шилина Н.Г. Руководство к
практическим занятиям по медицинской и
биологической статистике Красноярск: ООО
«Поликом». – 2003.

29. БЛАГОДАРЮ ЗА ВНИМАНИЕ