Уранения-неравенства-параметры

2.

Выражения
Общие методы решения уравнений и неравенств
У/н I и II степени
Модули
Иррациональные
Показательные
Логарифмические
Тригонометрические
Обратно-тригонометрические
Функционольные

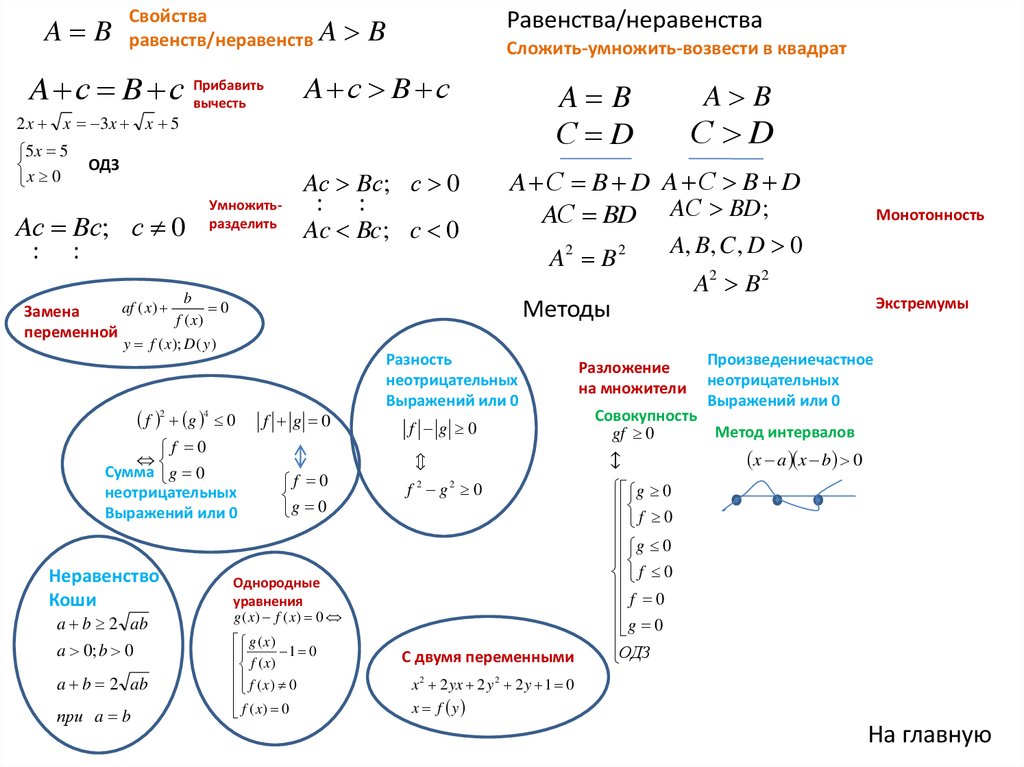
A B
Свойства
равенств/неравенств A
A с B с Прибавить
вычесть
Равенства/неравенства
B
Сложить-умножить-возвести в квадрат
A с B с
A B
С D
2 x x 3 x x 5
5 x 5
x 0
ОДЗ
Aс Bс; с 0
:
Умножитьразделить
:
Aс Bс; с 0
: :
Ac Bc ; c 0
b
af ( x)
0
Замена
f ( x)
переменной
y f ( x); D( y )
f 2 g 4 0
f 0
Сумма g 0
неотрицательных
Выражений или 0
Неравенство
Коши
a b 2 ab
a 0; b 0
a b 2 ab
при a b
f g 0
f 0
g 0
С D
A С B D A С B D
AС BD AС BD ;
A, B, C , D 0
A2 B 2
A2 B 2
Методы
Разность
неотрицательных
Выражений или 0
f g 0
f 2 g2 0
Однородные
уравнения
g ( x) f ( x) 0
g ( x)
f ( x) 1 0
f ( x) 0
f ( x) 0
A B
С двумя переменными
Разложение
на множители
Совокупность
gf 0
Монотонность
Экстремумы
Произведениечастное
неотрицательных
Выражений или 0
Метод интервалов
x a x b 0
g 0
f 0
g 0
f 0
f 0
g 0
ОДЗ
x 2 2 yx 2 y 2 2 y 1 0
x f y
На главную

4.

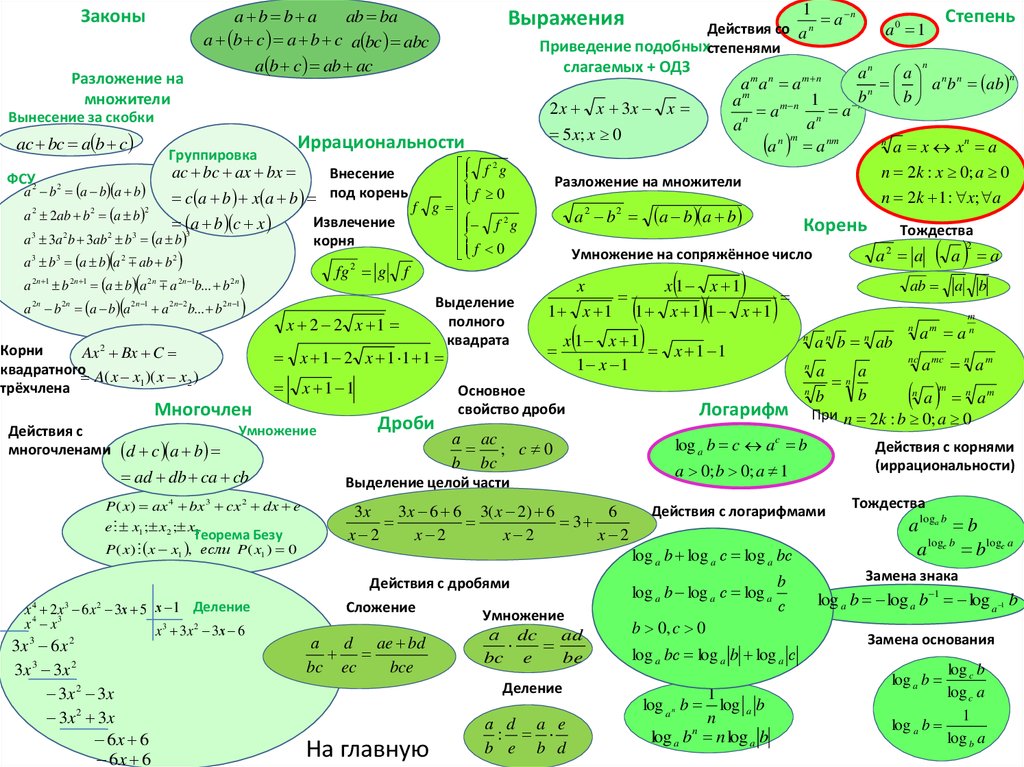
a b b a
ab ba
a b c a b c a bc abc
a b c ab ac
Законы
Разложение на
множители
Вынесение за скобки
ac bc a b c
Иррациональности
Группировка
f g
Внесение
a b a b a b
c a b x a b под корень f g f 0
2
a 2 2ab b 2 a b
Извлечение
f 2 g
3a b c x
3
2
2
3
a 3a b 3ab b a b
корня
f 0
3
3
2
2
a b a b a ab b
2
fg g f
2 n 1
2 n 1
2n
2 n 1
2n
ФСУ2
ac bc ax bx
2n
a b a a
a b a b a
2n
2 n 1
a
2n 2
b... b
b... b
2 n 1
Корни
Ax 2 Bx C
квадратного
A( x x1 )( x x2 )
трёхчлена
x 2 2 x 1
x 1 1
Многочлен
Действия с
многочленами d c a b
Выделение
полного
квадрата
x 1 2 x 1 1 1
Умножение
ad db ca cb
P ( x ) ax 4 bx 3 cx 2 dx e
e x1 ; x2 ; x3
Теорема Безу
P ( x ) x x1 , если P ( x1 ) 0
Разложение на множители
Дроби
3x 3 6 x 2
3x 3 3x 2
3x 2 3x
3x 2 3x
6x 6
6x 6
2
a a
Основное
свойство дроби
а ac
; c 0
b bc
Умножение
а dc
ad
bc e
be
а d a e
:
b e b d
a a
ab
x 1 x 1
x 1 1
1 x 1
Деление
На главную
Тождества
2
x
x 1 x 1
1 x 1 1 x 1 1 x 1
3x
3x 6 6 3( x 2) 6
6
3
x 2
x 2
x 2
x 2
а d ae bd
bc ec
bce
Корень
Умножение на сопряжённое число
Выделение целой части
Сложение
n 2k 1 : x; a
a b a b
a b
2
Действия с дробями
x 44 23x 3 6 x 2 3х 5 х 1 Деление
x x
x 3 3x 2 3х 6
n 2k : x 0; a 0
2
2
b
a
1
Степень
a n
Действия со a n
a0 1
Приведение подобныхстепенями
n
слагаемых + ОДЗ
an a n n
n
a m a n a m n
a b ab
n
m
b
b
1
a
2 x x 3x x
a m n n a n
n
a
a
5 x; x 0
n m
n
a
a nm
a x xn a
Выражения
2
a
b
m
n
a b ab
n
n
n
am a n
nc mc
a n am
a n a
m
n
n
Степень
b
b
a n am
Логарифм При n 2k : b 0; a 0
n
log a b c a c b
Действия с корнями
(иррациональности)
a 0; b 0; a 1
Действия с логарифмами
log a b log a с log a bс
b
log a b log a с log a
с
b 0, c 0
log a bс log a b log a с
1
log a b
n
log a bn n log a b
log a n b
Тождества
a loga b b
a logс b b logс a
Замена знака
log a b log a b 1 log a 1 b
Замена основания
log c b
log c a
1
log a b
log b a
log a b

5.

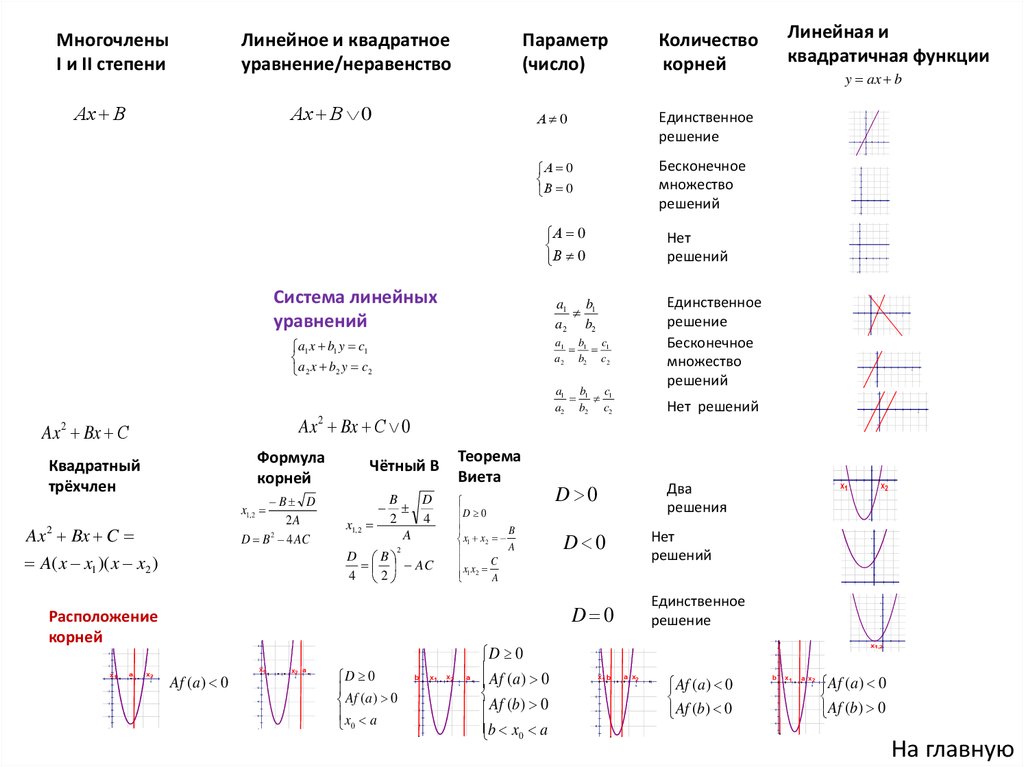
Многочлены
I и II степени
Линейное и квадратное
уравнение/неравенство
Аx В
Параметр
(число)
Аx В 0
Линейная и
квадратичная функции
Количество
корней
А 0
y ax b
Единственное
решение
4
2
-2
Бесконечное
множество
решений
А 0
В 0
4
2
-2
А 0
В 0
Нет
решений
4
2
-2
Система линейных
уравнений
a1 x b1 y c1
a2 x b2 y c2
a1 b1 c1
a2 b2 c2
a1 b1 c1
a2 b2 c2
Ax Bx С 0
2
Ax Bx С
2
Формула
корней
Квадратный
трёхчлен
B D
x1, 2
2A
D B 2 4 AC
Ax Bx C
2
Теорема
Виета
D 0
B
x1 x2
A
C
x1 x2 A
B
D
2
4
A
2
D B
AC
4 2
A( x x1 )( x x2 )
4
4
4
2
2
x1
а
x2
5
-2
-4
-6
-8
Af (a) 0
x1
x2 а
5
-2
-4
-6
-8
D 0
Af (a ) 0
x a
0
5
-2
2
5
-2
2
Нет решений
D 0
5
Два
решения
2
b
x1
а
x2
5
-2
-4
-6
D 0
Af (a ) 0
Af (b) 0
b x0 a
-5
x1
x2
-2
-4
D 0
Нет
решений
6
4
2
x1
Единственное
решение
D 0
Расположение
корней
2
-2
Чётный В
x1, 2
Единственное
решение
Бесконечное
множество
решений
a1 b1
a2 b2
x2
6
4
2
6
x1,2
4
x2
4
2
2
x1 b
а x2
5
-2
-4
-6
Af (a) 0
Af (b) 0
b
x1
а x2
5
-2
-4
Af (a) 0
Af (b) 0
-6
На главную

6.

4
3
2
Биквадратные x ax bx ax 1 0
1 Возвратные
x 4 ax 2 b 0
y x2 ; y 0
y x
x

7.

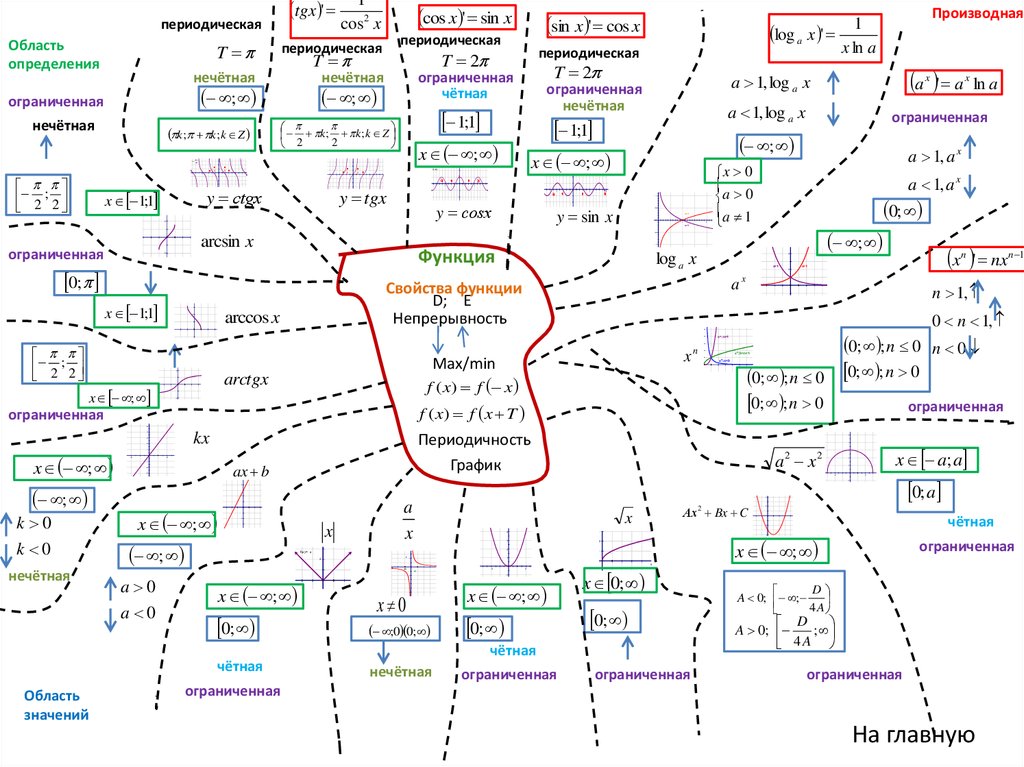
tgx '
периодическая
Область
определения
T
периодическая
нечётная
нечётная
k; k; k Z
f x =
-
-
2
;
2
f x = tg x
2
-
5
-
2
2
-5
f x = cos x
2
5
-2
-2
y сtgx
1;1
x ;
2
-2
x 1;1
ограниченная
нечётная
1;1
x ;
k ; k ; k Z
2
2
T 2
ограниченная
чётная
-
1
-5
y tgx
2
5
-5
-2
-
5
10
2
1
-2
y сosx
2
a 1, log a x
a ' a
a 1, log a x
ограниченная
x
;
2
-2
y sin x
0,5
a<1
1
2
a>1
arcsin x
x 0
a 0
a 1
0;
0;
x 1;1
arccos x
2
log a x
;
4
a<1
-2
f ( x) f x T
ограниченная
2
0; ; n 0
0; ; n 0
xn;0<n<1
xn;n<0
n 1
n 1,
xn;n>1
5
f ( x) f x
arctgx
x ;
xn
Max/min
2
n
ax
4
2 ; 2
x ' nx
a>1
2
Свойства функции
D; E
Непрерывность
ln a
a 1, a x
-1
Функция
-2
x
a 1, a x
-0,5
ограниченная
Производная
log a x ' 1
x ln a
периодическая
T 2
sin x
sin x ' cos x
периодическая
cos x
-5
2 ; 2
cos x ' sin x
T
;
ограниченная
нечётная
1
cos2 x
0; ; n 0
0; ; n 0
0 n 1,
n 0
ограниченная
5
4
kx
3
2
x ;
Периодичность
График
1
-2
2
ax b
-1
-2
-3
5
x a; a
4
a x
2
3
2
2
1
-2
2
-1
;
k 0
k 0
нечётная
4
2
x ;
4
-2
x
;
a
x
a 0
x
x ;
2
1
2
g
-2
-4
x 0
-6
0;
;0 0;
чётная
нечётная
2
-1
-2
x ;
x ;
0;
x 0;
ограниченная
ограниченная
5
0;
чётная
Область
значений
чётная
-4
3
2
f
2
0; a
2
-2
4
f x = x
x0
a 0
Аx 2 Bx C
ограниченная
D
A 0; ;
4A
D
A 0;
;
4A
ограниченная
ограниченная
На главную

8.

log h fg c
сtg f сtg g
arccos(-x)
f g n
n
ОДЗ
arccosx
-x
x
tg f tg g
arcsin f arcsin g
f g
f 1
ОДЗ
arcsinx x
arcsin(-x)-x
сtgx
сtgx
f g n
n
ОДЗ
tgx
tgx
f g
f 1
f g
f 1
arctg f arctg g
f g
f g
f 0
f g
f 0
ОДЗ
f h
f g
f g
g 0
ОДЗ
f g
f g
f g
ОДЗ
f g 2 n
n
ОДЗ
сosx x
cos
sin x
arcsin x
Отбрасывание
функций
Эквивалентные
системы
arccos f arccos g
arccos f arccos g
cos f cos g
log h f log h g c ОДЗ
log h f log h g c
log h fg c f 0
f 0
f g 2 n
g 0
f
g
2
m
log ( f ) log ( g ) c
g 0
h
h
ОДЗ
n, m
f 0
ОДЗ
g 0
sin x
log h f log h g 0
log h f 0
sin f sin g
arccos x
h 1
log a x
ax
arctgx
f g
ОДЗ
f 2 h2
ОДЗ
f g
f g
f g
ОДЗ
h 1
Логарифмирование
a 1
x
a 1
a
x
x
f u
g v
fv ug gv 0
gv 0
ОДЗ
f g
f g
f 0
ОДЗ
( h 1)( f g ) 0
log h f 0 0
h
0
;
h
1
;
f
0
;
g
0
ОДЗ
g
(a 1)( f g ) 0
a 0
ОДЗ
f n gm
f ( x) g ( x)
f ( x) g 2 ( x)
g ( x) 0
На главную
fh g
a a 0
f
h log f g
f 0; g 0; f 1
ОДЗ
f n gm
ОДЗ
f ( x) g ( x)
f ( x) g 2 ( x)
g ( x) 0
f ( x) 0
g ( x) 0
f ( x) g ( x)
f ( x) g 2 ( x)
g ( x) 0
f ( x) 0

9.

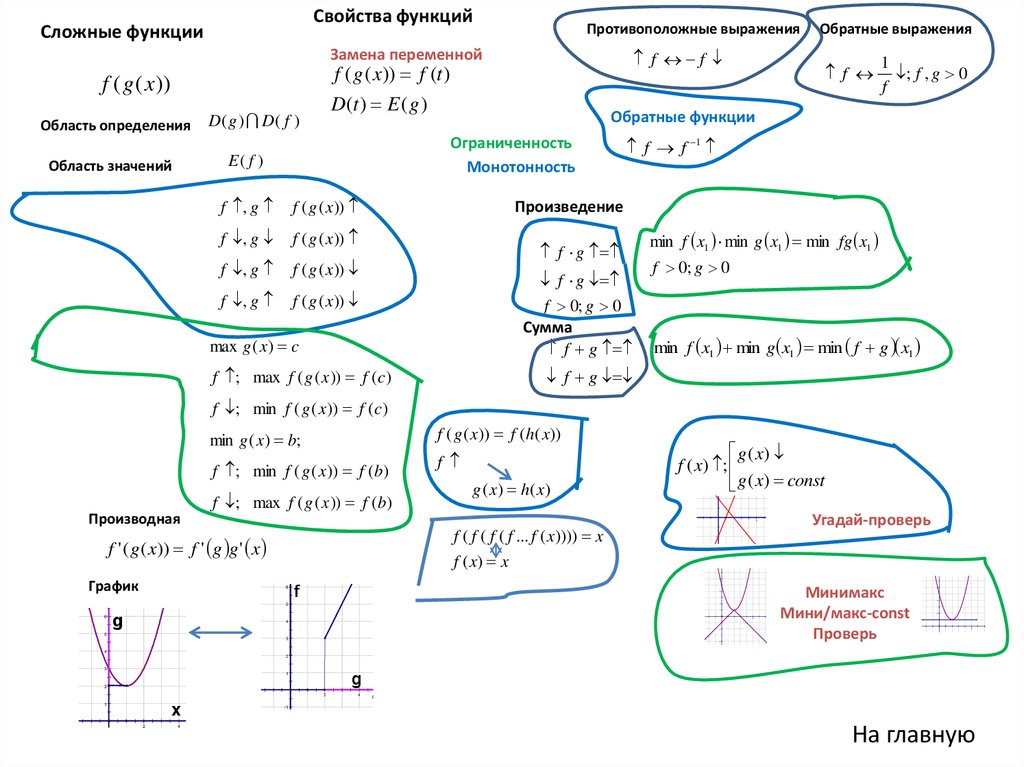
Свойства функций
Сложные функции
Противоположные выражения
Замена переменной
f f
f ( g ( x)) f (t )
f ( g ( x ))
Область определения
D(t ) E ( g )
D( g ) D( f )
f , g
f ( g ( x))
f , g
f ( g ( x))
f , g
f ( g ( x))
f , g
f ( g ( x))
f
1
; f , g 0
f
Обратные функции
Ограниченность
Монотонность
E( f )
Область значений
Обратные выражения
f f 1
Произведение
f g
f g
f 0; g 0
Сумма
f g
max g ( x ) c
min f x1 min g x1 min fg x1
f 0; g 0
min f x1 min g x1 min f g x1
f g
f ; max f ( g ( x )) f ( c )
f ; min f ( g ( x )) f ( c )
f ( g ( x)) f (h( x))
min g ( x ) b;
f ; min f ( g ( x )) f (b)
f ; max f ( g ( x )) f (b)
Производная
g ( x ) h( x )
g ( x)
f ( x) ;
g ( x) const
2
5
f ( f ( f ( f ... f ( x)))) x
f ' ( g ( x)) f ' g g ' x
Угадай-проверь
-2
f ( x) x
6
График
6
f
4
5
6
f
g
2
5
4
-2
5
3
-4
Минимакс
Мини/макс-const
Проверь
6
4
2
5
4
2
3
1
g
2
2
1
x
2
4
4
g x = 1,5 x
-1
На главную

10.

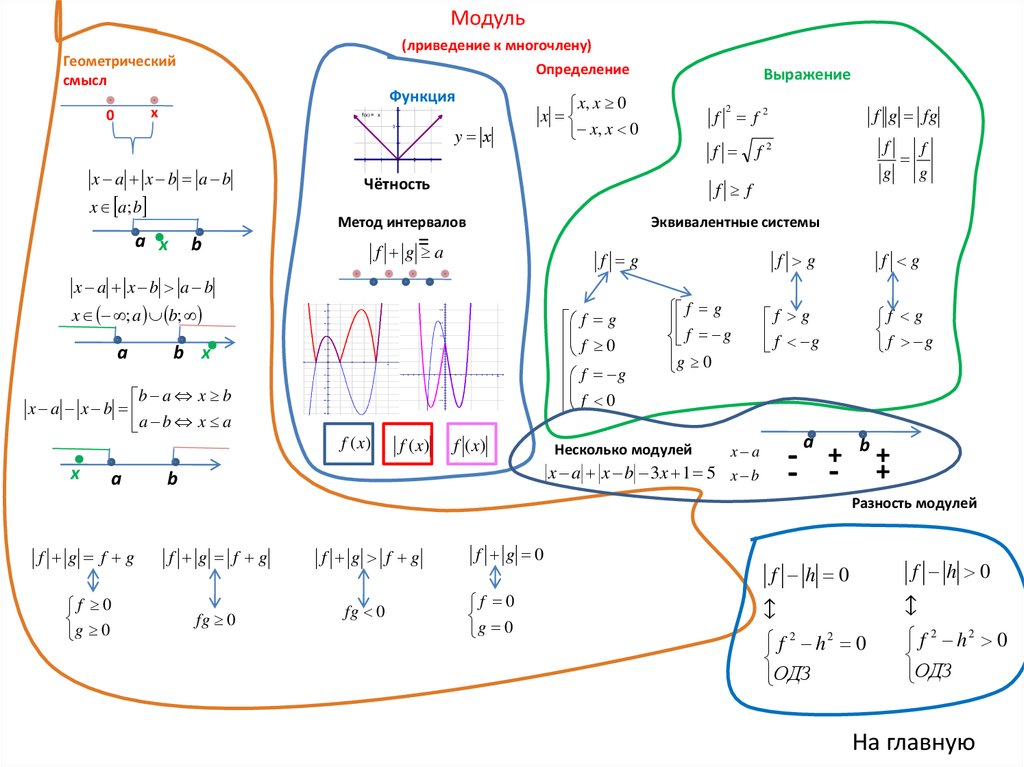
Модуль
(лриведение к многочлену)
Геометрический
смысл
Определение
Функция
х
0
x, x 0
x
x , x 0
f x = x
y х
2
x a x b a b
x a; b
а x
Выражение
f
2
f g fg
f2
f
f
f2
g
Чётность
f f
Метод интервалов
Эквивалентные системы
b
=
g a
f
f g
f
g
f g
f g
f g
f g
f g
f g
x a x b a b
x ; a b;
25
8
20
6
15
4
а
b x
10
2
5
5
-2
10
b a x b
x a x b
a b x a
-4
-5
-6
-10
-8
f (x)
x
а
f (x)
f (x)
f
f
f
f
g
0
g
f g
f g
g 0
0
Несколько модулей
а
-- +- b ++
x a
x a x b 3x 1 5 x b
b
Разность модулей
f g f g
f g f g
f 0
g 0
fg 0
f g f g
fg 0
f g 0
f 0
g 0
f h 0
f h 0
f 2 h2 0
ОДЗ
f 2 h2 0
ОДЗ
На главную

11.

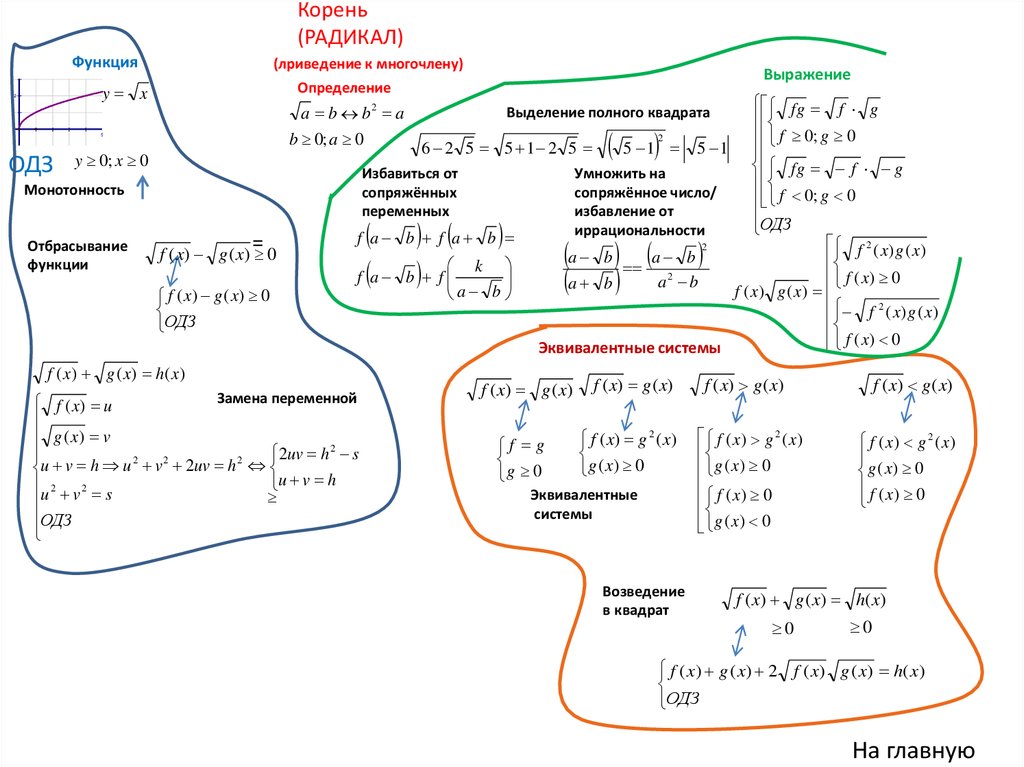
Корень
(РАДИКАЛ)
Функция
y x
(лриведение к многочлену)
Выражение
Определение
fg f g
2
f 0; g 0
b 0; a 0
6 2 5 5 1 2 5
5 1 5 1
fg f g
ОДЗ y 0; x 0
Избавиться от
Умножить на
Монотонность
сопряжённых
сопряжённое число/
f 0; g 0
переменных
избавление от
ОДЗ
иррациональности
f
a
b
f
a
b
=
f 2 ( x) g ( x)
2
Отбрасывание
f ( x) g ( x) 0
a
b
a
b
функции
k
2
f a b f
f ( x) 0
a b
a b
a
b
f
(
x
)
g
(
x
)
f ( x) g ( x) 0
f 2 ( x) g ( x)
ОДЗ
f ( x) 0
Эквивалентные системы
f ( x ) g ( x ) h( x )
f ( x) g ( x)
f ( x) g ( x)
f ( x) g ( x) f ( x) g ( x)
Замена переменной
f ( x) u
g ( x) v
f ( x) g 2 ( x) f ( x ) g 2 ( x )
f ( x) g 2 ( x)
f
g
2
2
uv
h
s
2
2
2
u v h u v 2uv h
g ( x) 0
g ( x) 0
g 0
g ( x) 0
u v h
u 2 v 2 s
f ( x) 0
Эквивалентные
f ( x) 0
системы
ОДЗ
g ( x) 0
2
a b b2 a
Выделение полного квадрата
5
Возведение
в квадрат
f ( x) g ( x) h( x)
0
0
f ( x ) g ( x ) 2 f ( x ) g ( x ) h( x )
ОДЗ
На главную

12.

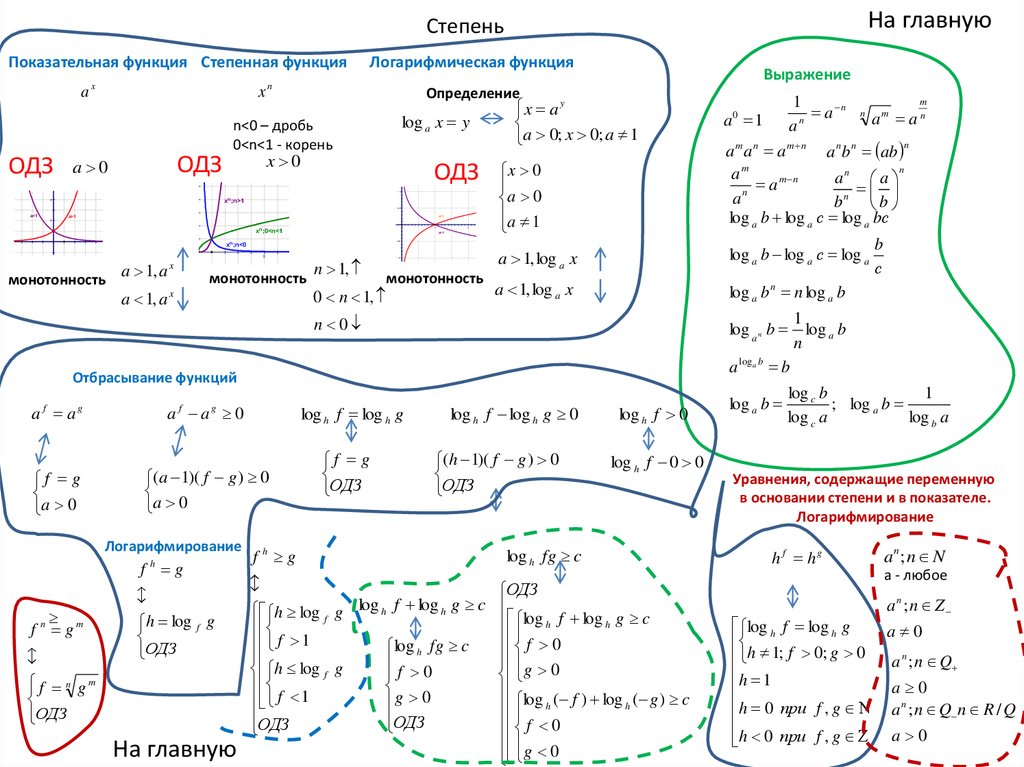
На главную
Степень
Показательная функция Степенная функция
a
ОДЗ
x
x
ОДЗ
a 0
Логарифмическая функция
n
log a x y
n<0 – дробь
0<n<1 - корень
x 0
ОДЗ
1
xn;n>1
4
4
0,5
a<1
a>1
a<1
2
2
1
xn;0<n<1
5
a 1, a x
a 1, a
2
a>1
x a y
a 0; x 0; a 1
монотонность
x
n 1,
0 n 1,
-1
монотонность
a 1, log a x
log a b log a с log a
a 1, log a x
log a b n n log a b
log a n b
a f ag 0
f g
a 0
(a 1)( f g ) 0
a 0
f n gm
h log f g
ОДЗ
f n g m
ОДЗ
На главную
m
n
b
с
1
log a b
n
a loga b b
a f ag
a a
m
x 0
a 0
a 1
Отбрасывание функций
fh g
a 1
n
a m a n a m n a n b n ab n
n
am
m n
an a
a
an
bn b
log a b log a с log a bс
n 0
Логарифмирование
1
a n
n
a
0
-0,5
xn;n<0
монотонность
Выражение
Определение
log h f log h g
fh g
f g
ОДЗ
log h f log h g 0
(h 1)( f g ) 0
ОДЗ
log h f 0
log h f 0 0
log h fg c
ОДЗ
log
f
log
g
c
h
h
h log f g
log h f log h g c
f 0
f 1
log h fg c
f 0
h log f g
g 0
log ( f ) log ( g ) c
f
1
g
0
h
h
ОДЗ
ОДЗ
f 0
g 0
log a b
log c b
1
; log a b
log c a
log b a
Уравнения, содержащие переменную
в основании степени и в показателе.
Логарифмирование
h f hg
an ; n N
а - любое
an ; n Z
log h f log h g
a 0
h 1; f 0; g 0
a n ; n Q
h 1
a 0
h 0 при f , g a n ; n Q n R / Q
h 0 при f , g a 0

13.

функции
y sin x
y сosx
f x = cos x
2
-2
-
5
-
1
Определение
sin x 1; cos x 1
2
2
-5
sin x sin x sin x; n 2
2
5
-2
-2
E( y) 1;1
y сtgx
Периодические T 2
y tgx
f x =
f x = tg x
2
-5
-
-
2
2
5
-2
D( y ) k ; k ; k Z
2
2
Периодические
E( y) k; k; k Z
T
sin =cos
-
sin =- sin( + ) +
x
sin sin cos cos sin
sin x x tgx; x 0;
2
Формулы приведения
sin = sin( - )
-x
sinx x
-2
Геометрический
смысл
2
-
Разложение на
множители
2
-
sin
sin sin cos cos sin
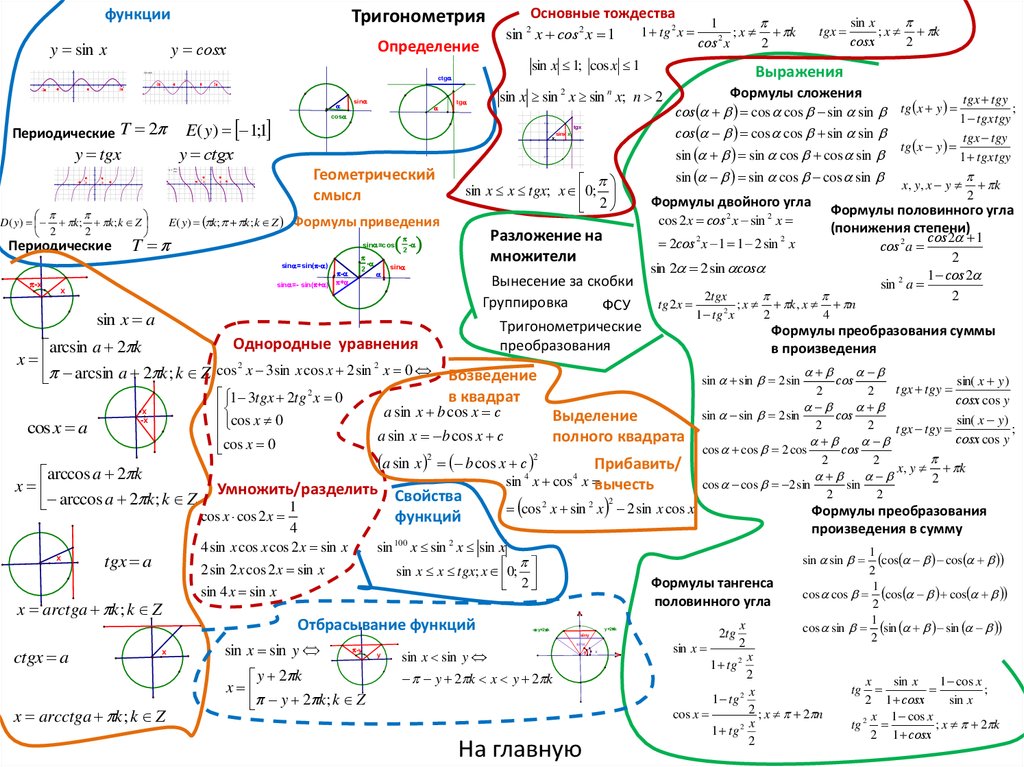
Формулы двойного угла
cos x a
cos x 0
cos x 0
arccos a 2 k
x
arccos a 2 k ; k Z
x
tgx a
tg 2 x
Умножить/разделить
1
4
4 sin x cos x cos 2 x sin x
cos x cos 2 x
x
x arcctga k ; k Z
Свойства
функций
Отбрасывание функций
sin x sin y
Прибавить/
sin 4 x cos 4 x вычесть
2
cos 2 x sin 2 x 2 sin x cos x
sin 100 x sin 2 x sin x
sin x x tgx; x 0;
2
sin 4 x sin x
-y
y 2 k
x
y 2 k ; k Z
k
2
1 сos 2
sin a
2
сos
sin( x y )
tgx tgy
2
2
сosx cos y
sin sin 2 sin
сos
sin( x y )
2
2
tgx tgy
;
сosx
cos y
cos cos 2 cos
сos
2
2
x, y k
2
cos cos 2 sin
sin
2
2
Формулы преобразования
произведения в сумму
1
cos cos
2
1
cos cos cos cos
2
1
cos sin sin sin
2
sin sin
Формулы тангенса
половинного угла
y+2 k
- -y+2 k
siny
sinx
y
2tgx
; x k , x n
2
1 tg x
2
4
sin sin 2 sin
a sin x 2 b cos x с 2
2
Формулы преобразования суммы
в произведения
Выделение
полного квадрата
a sin x b cos x с
2 sin 2 x cos 2 x sin x
x arctga k ; k Z
ctgx a
a sin x b cos x с
2
arcsin a 2 k
x
2
2
arcsin a 2 k ; k Z cos x 3 sin x cos x 2 sin x 0 Возведение
1 3tgx 2tg 2 x 0
в квадрат
x
-x
x, y , x y
сos a
sin 2 2 sin сos
Тригонометрические
преобразования
Однородные уравнения
tgx tgy
;
1 tgxtgy
tgx tgy
tg x y
1 tgxtgy
tg x y
Формулы половинного угла
(понижения степени)
сos 2 1
2
cos 2 x сos 2 x sin 2 x
2сos 2 x 1 1 2 sin 2 x
Вынесение за скобки
Группировка
ФСУ
sin x a
Формулы сложения
сos cos cos sin sin
сos cos cos sin sin
tgx
x
2
-5
5
-2
tg
2
sin x
n
cos
cos x
2
- 2
sin
sin x
; x k
сosx
2
Выражения
ctg
10
tgx
2
2
-2
-5
Основные тождества
1
1 tg 2 x
; x k
sin x сos 2 x 1
сos 2 x
2
Тригонометрия
sin x sin y
y 2 k x y 2 k
На главную
y
x
sin x
2tg
x
2
x
2
x
1 tg 2
2
cos x
; x 2 n
x
1 tg 2
2
1 tg 2
x
sin x
1 cos x
;
2 1 сosx
sin x
x 1 cos x
tg 2
; x 2 k
2 1 сosx
tg

14.

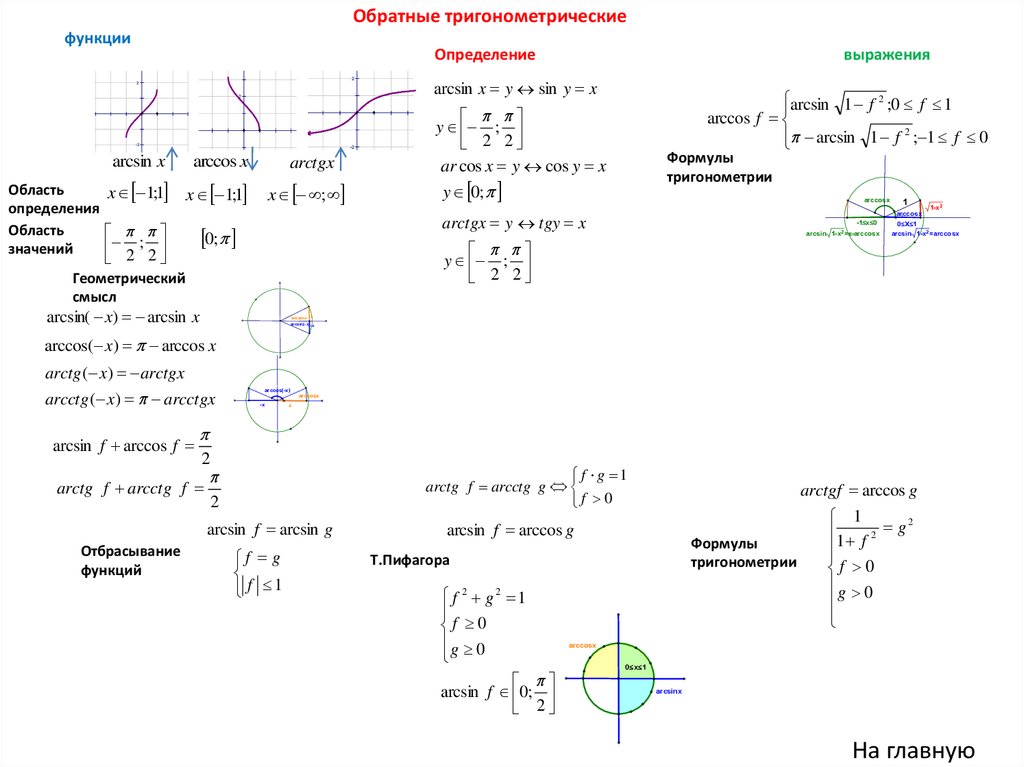
Обратные тригонометрические
функции
Определение
2
2
2
-2
arcsin x
Область
определения
Область
значений
-2
arccos x
arctgx
x 1;1 x 1;1
2 ; 2
x ;
выражения
arcsin x y sin y x
arcsin 1 f 2 ;0 f 1
arccos f
arcsin 1 f 2 ; 1 f 0
y ;
2 2
ar cos x y cos y x
Формулы
тригонометрии
y 0;
arccosx
arctgx y tgy x
0;
arcsin 1-x2 = -arccosx
y ;
2 2
Геометрический
смысл
arcsin( x) arcsin x
1
1-x2
arccosx
j
-1 x 0
0 x 1
arcsin 1-x2 =arccosx
arcsinx x
arcsin(-x)-x
arccos( x) arccos x
arctg ( x) arctgx
arcctg ( x) arcctgx
arcsin f arccos f
arccos(-x)
arccosx
-x
x
2
arctg f arcctg f
f g 1
arctg f arcctg g
f 0
2
arcsin f arcsin g
Отбрасывание
функций
f g
f 1
arctgf arccos g
arcsin f arccos g
Формулы
тригонометрии
Т.Пифагора
f 2 g2 1
f 0
g 0
arcsin f 0;
2
1
2
1 f 2 g
f 0
g 0
arccosx
0 x 1
arcsinx
На главную

15.

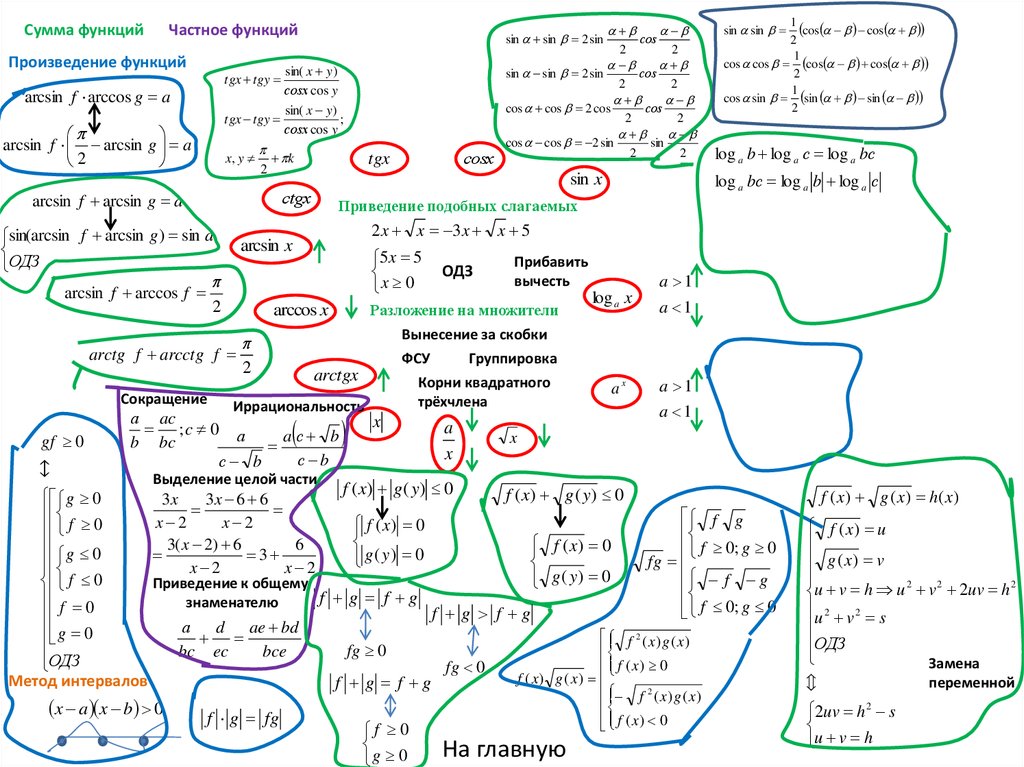
Сумма функций
Частное функций
Произведение функций
arcsin f arccos g a
arcsin f arcsin g a
2
sin( x y )
сosx cos y
sin( x y )
tgx tgy
;
сosx cos y
x, y
2
k
сosx
tgx
2
сos
2
сos
2
2
cos cos 2 cos
сos
2
2
cos cos 2 sin
sin
2
2
log a b log a с log a bс
Приведение подобных слагаемых
2 x x 3x x 5
5 x 5
x 0
ОДЗ
ФСУ
arctgx
Иррациональность
а ac
;c 0 а
a с b
b bc
с b
с b
Выделение целой части
Прибавить
вычесть
Разложение на множители
Вынесение за скобки
arccos x
2
1
cos cos
2
1
cos cos cos cos
2
1
cos sin sin sin
2
sin sin
log a bс log a b log a с
sin x
arcsin x
arctg f arcctg f
сtgx
sin(arcsin f arcsin g ) sin a
ОДЗ
arcsin f arccos f
2
gf 0
sin sin 2 sin
tgx tgy
arcsin f arcsin g a
Сокращение
sin sin 2 sin
a 1
Группировка
Корни квадратного
трёхчлена
x
a 1
log a x
a
x
ax
a 1
a 1
x
f ( x) g ( y) 0
f ( x) g ( y) 0
g 0
3x
3x 6 6
f g
x 2
x 2
f ( x) 0
f 0
f ( x) 0
3( x 2) 6
6
g 0
f 0; g 0
3
g ( y ) 0
fg
x 2
x 2
g ( y ) 0
f 0
f g
Приведение к общему
f
g
f
g
f 0; g 0
знаменателю
f g f g
f 0
а d ae bd
g 0
f 2 ( x ) g ( x )
fg 0
bc ec
bce
ОДЗ
f ( x ) 0
fg 0
f ( x) g ( x)
Метод интервалов
f g f g
f 2 ( x ) g ( x )
x a x b 0
f g fg
f ( x ) 0
f 0
На главную
g 0
f ( x ) g ( x ) h( x )
f ( x) u
g ( x) v
2
2
2
u v h u v 2uv h
u 2 v 2 s
ОДЗ
Замена
переменной
2uv h 2 s
u v h

16.

При каком а …
Функции
выражения
Решить
Параметры
уравнения
И
неравенства
Линейная функция
…
a ...; ; x f (a )
4
4
4
2
2
Нечётное количество
решений
Единственность решения? Симметрия
a 0
линейных
уравнений
2
2
2
5
1
b
2
1
2
4
6
-1
x2
x2
4
Расположение
Af (a) 0
корней
квадратного трёхчлена
2
x1
а
x2
5
-2
-4
-6
Бесконечное
D 0
множество решений
a1 b1 c1
a2 b2 c2
5
-2
2
a1 b1 c1
a2 b2 c2
2
Нет решений
4
2
Af (a ) 0
x a
0
x1
x2 а
5
-2
-4
-6
-2
Подобие
2
D 0
D 0
-8
5
-2
x1
D 0
x1,2
корни принадлежат промежутку?
-2
1
a 0
b 0
a1 x b1 y c1
a2 x b2 y c2
Единственное
a1 b1
решение
a2 b2
2
f x ax b
Поворот
3
2
-4
-2
Параллельный перенос
2
4
Единственное
Два
Нет
А 0
Бесконечное Нет
решение
решения
решений
множество
решений
Единственное
решений
Решение промежуток или
решение
Система
Движения плоскости + график
а
f x x a
-1
6
4
2
a 0
b 0
-2
1
х0
x2
-2
2
-1
x1
-2
3
-2
-5
-2
4
-2
6
2
n
x0 0 Необходимое условие
Квадратный трёхчлен
Количество
2
решений? Ax Bx C 0
ax b 0
a ;... ; x f1 (a )
На главную
-8
6
D 0
Af (a ) 0
Af (b) 0
b x0 a
4
2
b
x1
а
x2
5
-2
-4
-6
4
4
-1
-2
y
4
4
Вложенные
графики
g
g22
2
y=f(g)
g1
x1
5
x2
f g x h g x f g h g
g1
g x
g2
y=h(g)
g
g1 g2
g x = 2 x
x
f x1 g x1
f ' x1 g ' x1
Числовая прямая
a 5
x a
x 5
а
-
5
+
-
+ график
-
-3
5
а
+
a 5
+
+
а x2
5
-2
Af (a) 0
Af (b) 0
2
x1 b
а x2
5
-2
-4
-4
-6
-6
Af (a) 0
Af (b) 0
-1
-2
-3
-4
Теорема Виета
Выделение целой части
-1
x1
2
4
-2
x 5 x a 3 x
+
+
2
b
х
-2
1
-2
2
c
c
f g ; g; Z
a
a
k x k 2; k Z
b
x1 x2 Z
a
c
x1 x2 Z
a
Решение – целое число
Решение при любом
значении переменной
Выгодная точка
Решение при любом
значении параметра

English Русский Rules