Эквивалентные бесконечно малые функции

1. Математический анализ

7. Эквивалентные
бесконечно малые
функции.

2. Эквивалентные бесконечно малые

lim
1 α и β – эквивалентные б.м.
x x
(асимптотически равные) при х→х0
0
α~β
Теорема. Предел отношения двух бесконечно малых функций
не изменится, если каждую или одну из них заменить
эквивалентной ей бесконечно малой.
1
lim
lim
x x
x x
1
α ~ α1 β ~ β1 при х→х0
0
0
1
1 1
1 1
lim lim lim
lim
x x
x x
x x
x x
1
1
1
1
1
0
0
0
0

3. Теоремы о эквивалентных б.м.

Теорема. Разность двух эквивалентных бесконечно малых
есть бесконечно малая более высокого порядка:
Обратное утверждение. Если разность двух бесконечно
малых есть бесконечно малая высшего порядка, чем каждая
из них, то они являются эквивалентными бесконечно
малыми.
α ~ β ↔ (α – β)=о(α) и (α – β)=о(β).
Теорема. Сумма конечного числа бесконечно малых
функций разных порядков эквивалентна слагаемому низшего
порядка.
α=о(β), то α+β=о(β)+β ~ β .
Следствие: Для того чтобы функции были эквивалентными
при х→х0 необходимо и достаточно, чтобы
f ( x) g ( x) o( g ( x))

4. Таблица эквивалентных функций

sin x ~ x x 0
tg x ~ x
arcsin x ~ x
arctg x ~ x x 2
1 – cos x ~
2
ln(1 + x) ~ x
e x– 1 ~ x
a x – 1 ~ x∙lna
x
loga(1 + x) ~
ln a
(1 + x)m – 1 ~ m∙x
sin x = x +o(x)
tg x = x +o(x)
arcsin x = x +o(x)
arctg x = x +o(x)
x2
2
o
(
x
)
1 – cos x = 2
ln(1 + x) = x +o(x)
e x – 1 = x +o(x)
a x = 1 + x∙lna +o(x)
x
loga(1 + x) = ln a o( x)
(1 + x)m = 1 + m∙x +o(x)

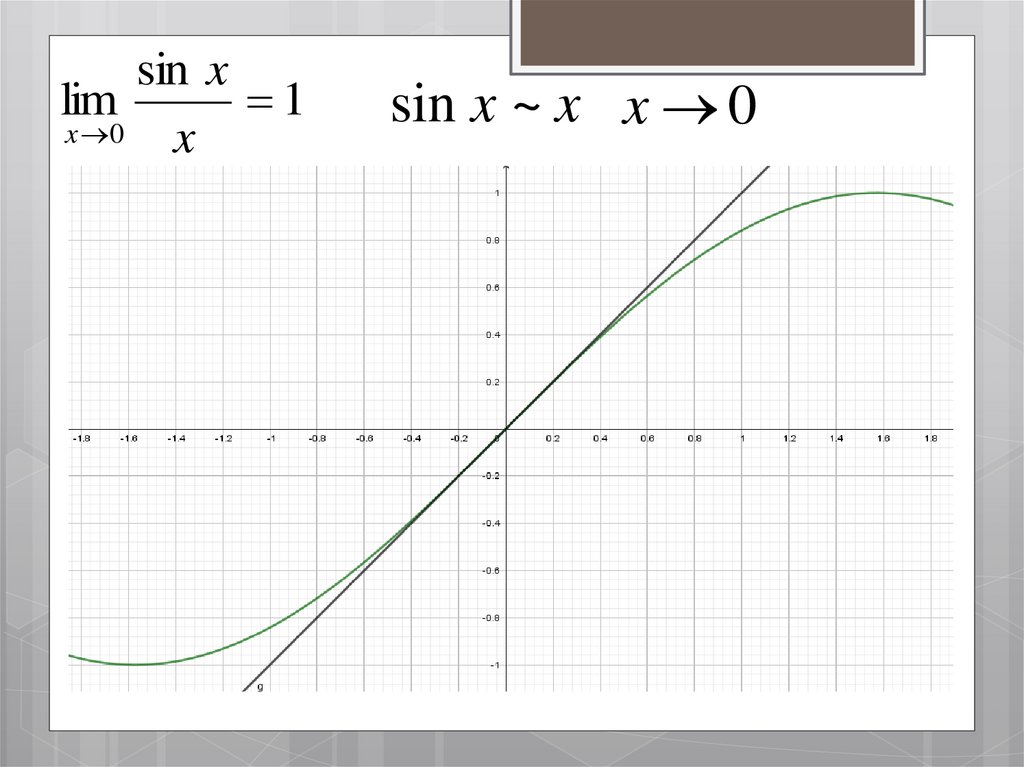
5.

sin x
lim
1
x 0
x
sin x ~ x x 0

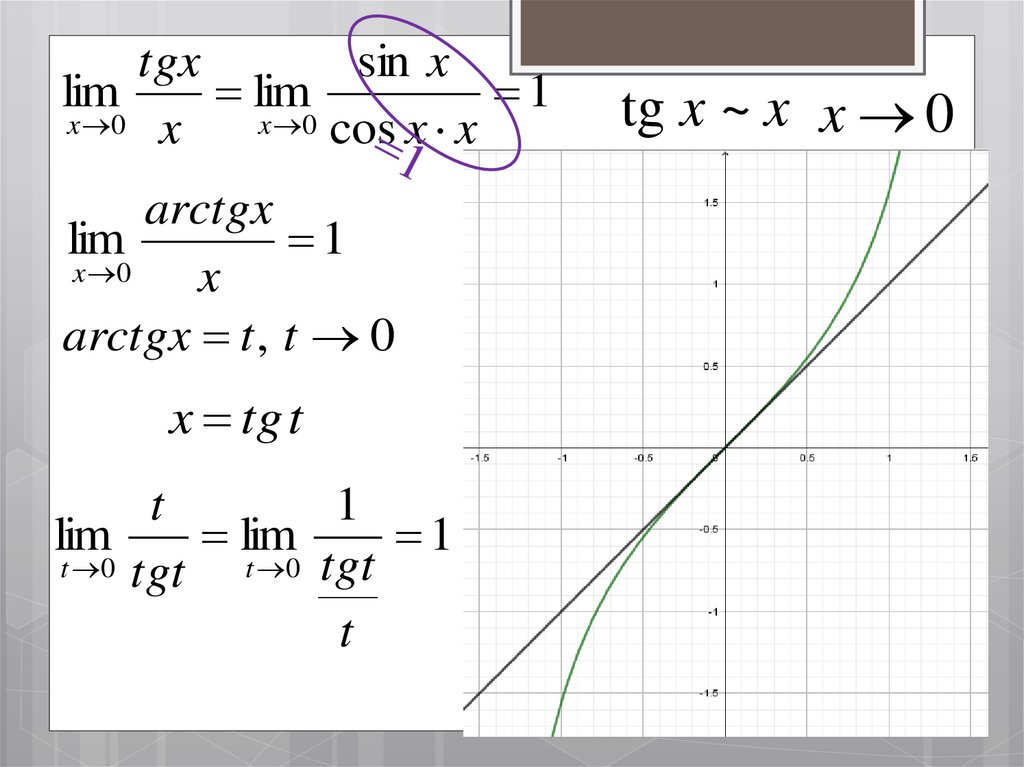
6.

tgx
sin x
lim
lim
1
x 0 x
x 0 cos x x
arctgx
lim
1
x 0
x
arctgx t , t 0
x tg t
t
1
lim
lim
1
t 0 tgt
t 0 tgt
t
tg x ~ x x 0

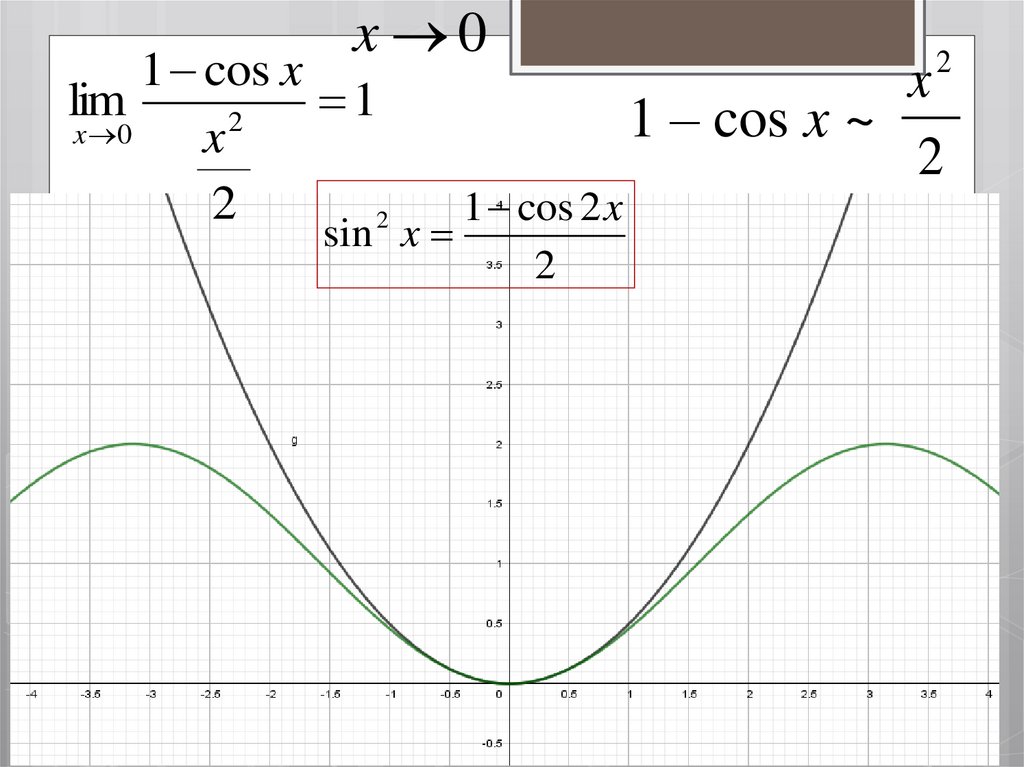
7.

x 0
1 cos x
lim
1
2
x 0
x
2
2
2
1 cos 2 x
sin x
2
x
1 – cos x ~
2
x
x
x
2 sin
sin
sin
1 cos x
2 lim
2
2 1
lim
lim
2
2
x
0
x 0
x 0
x
x
x
x
2
2
2
2
2

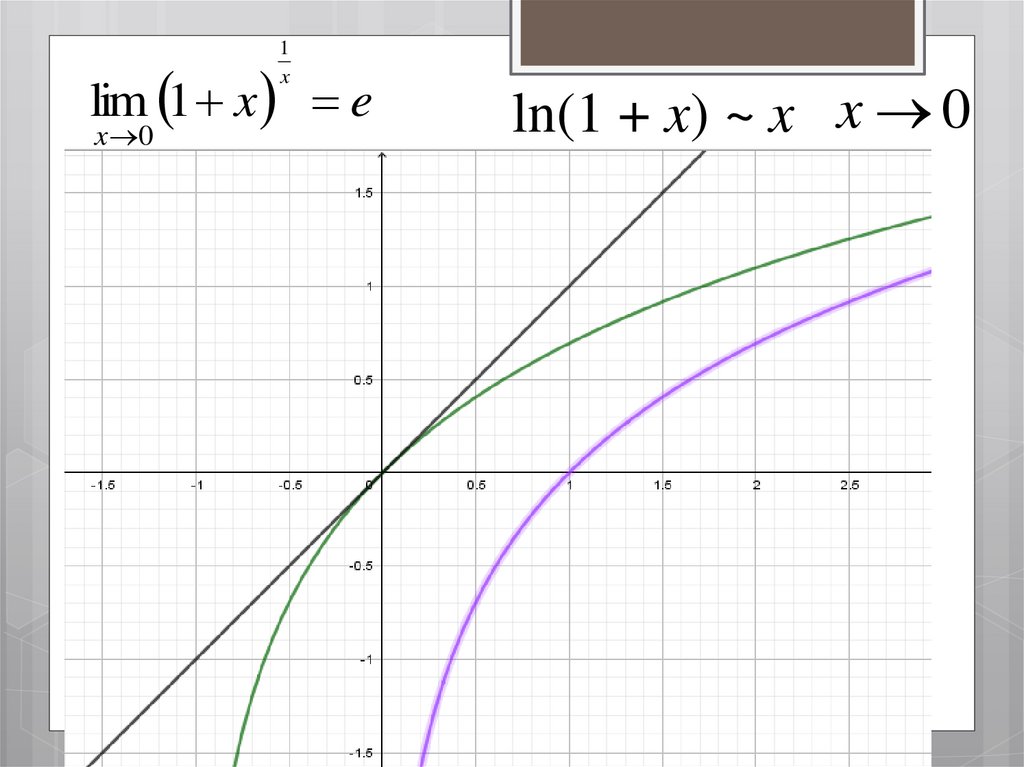
8.

1
x
lim 1 x e
x 0
ln lim 1 x ln e
x 0
1
x
1
x
lim ln 1 x 1
x 0
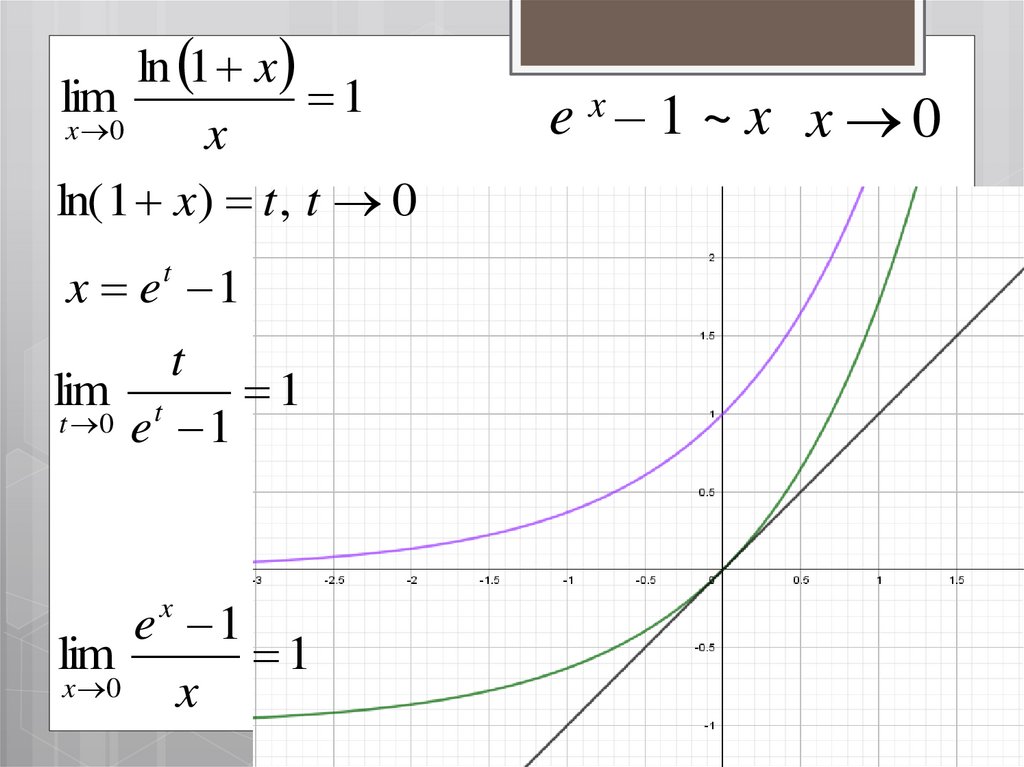
ln 1 x
lim
1
x 0
x
ln(1 + x) ~ x x 0

9.

ln 1 x
lim
1
x 0
x
ln( 1 x) t , t 0
x e 1
t
t
lim t
1
t 0 e 1
e 1
lim
1
x 0
x
x
e x– 1 ~ x x 0

10.

Математический
8. Функции.
анализ
Элементарные
функции.

11.

Отображением множества А в множество В
(функцией из А в В) называется подмножество
F декартова произведения этих множеств АxВ,
если для любого х существует единственный у,
x A ! y B : ( x; y ) F
т.е. для любых x, y, z из того, что ( x; y ) F ,
( x; z ) F , следует, что у=z, т.е. нет пар с
одинаковыми первыми, но различными
вторыми компонентами.
xF y
F : A B
F
A B
y F (x)
образ элемента х
прообраз элемента у

12.

Х и Y – непустые множества.
Функцией f называется соответствие, которое
каждому элементу х из X сопоставляет один и
только один элемент у множества Y.
y f (x)
f : X Y
X – область определения D(f) или Dom(f)
(от англ. domain — «область»)
Y – множество значений E(f) или R(f)
(от англ. range)

13.

Способы задания функций
Табличный.
Аналитический (одна или несколько формул или
уравнений).
Графический (график функции).
4 3
V ( R) R
3
y 1 x2
1, x 0,
y sgn x 0, x 0,
1, x 0.
x 2 cos t ,
y 2 sin t
x 2 y 2 4, y 0
Параметрическая
функция
Неявно заданная
функция

14.

График функции
График функции y=f(x) – множество всех точек
плоскости хОу, для каждой из которых х является
значением аргумента, а у – соответствующим
значением функции, т.е. точки (х; f(x)).
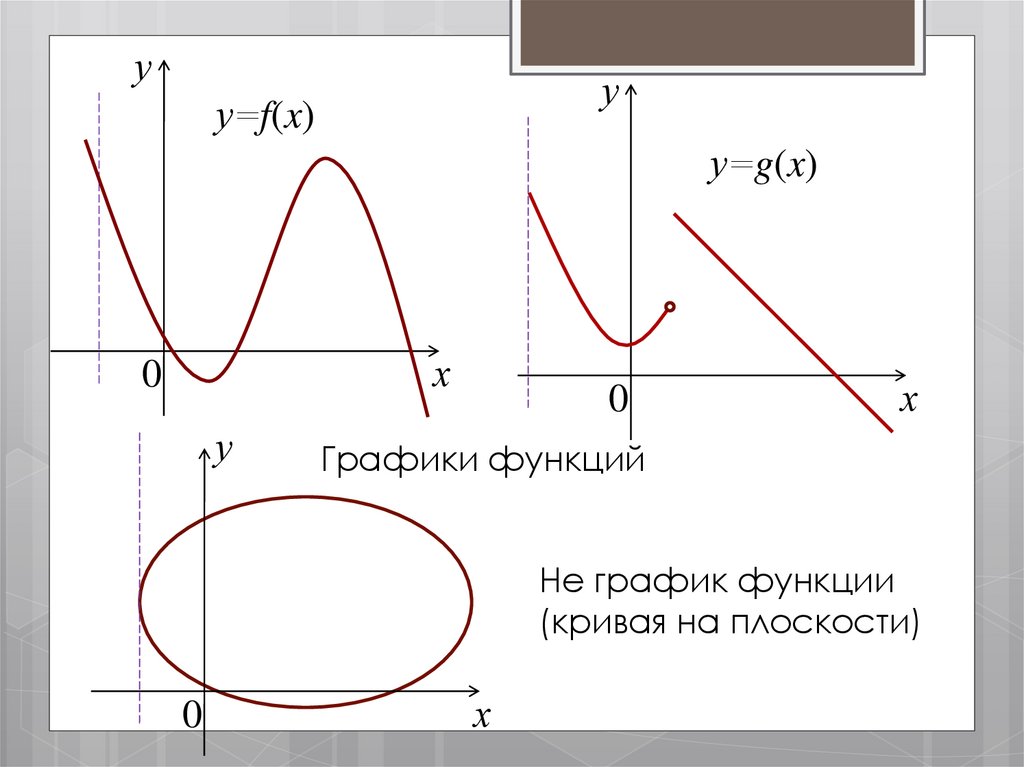
График функции y=f(x) – кривая на плоскости хОу
такая, что если через каждую точку х множества Х,
провести прямую параллельную оси Оу, то она
будет пересекать эту кривую только в одной точке.

15.

у
у
у=f(x)
у=g(x)
х
0
у
0
х
Графики функций
Не график функции
(кривая на плоскости)
0
х

16.

Область определения D(f) функции
- множество на котором функция задана и определена.
1
g ( x) 0
y
g ( x)
y log a g ( x) g ( x) 0
y arcsin g ( x)
y 2 n g ( x) g ( x ) 0
y arccos g ( x) g ( x) 1
y tg ( g ( x)) g ( x)
2
n, n Z
y сtg ( g ( x)) g ( x) n, n Z

17.

Основные характеристики
функций
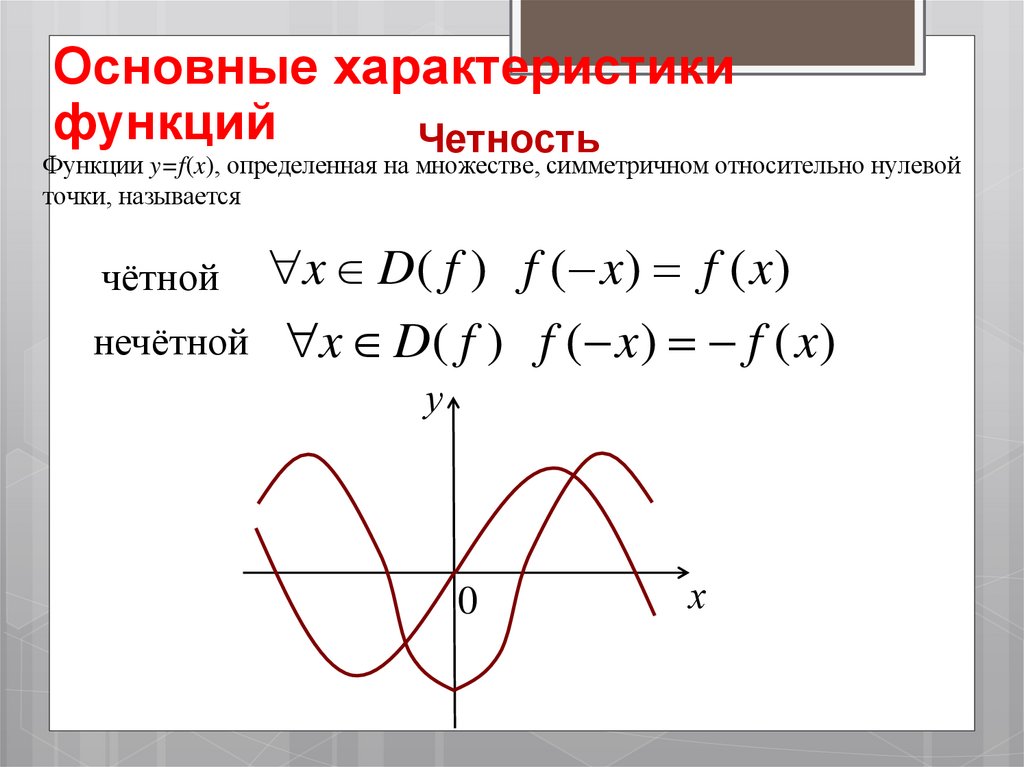
Четность
Функции y=f(x), определенная на множестве, симметричном относительно нулевой
точки, называется
x D( f ) f ( x) f ( x)
нечётной x D( f ) f ( x) f ( x)
чётной
у
0
х

18.

Основные характеристики
функций
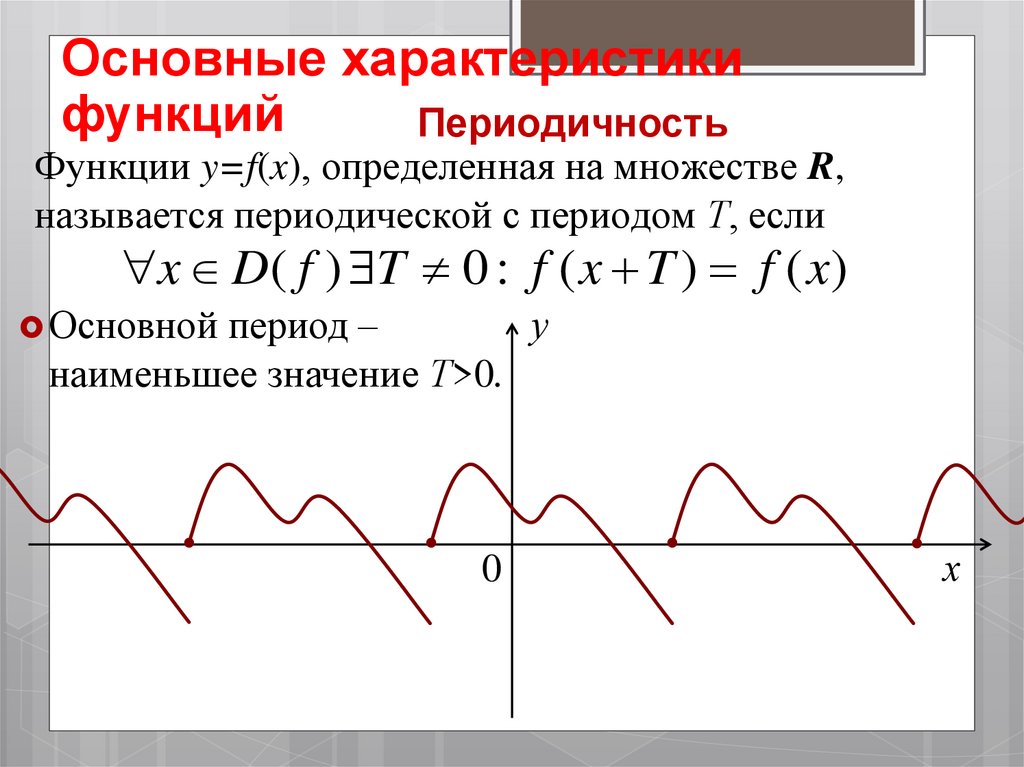
Периодичность
Функции y=f(x), определенная на множестве R,
называется периодической с периодом Т, если
x D( f ) T 0 : f ( x T ) f ( x)
Основной период –
у
наименьшее значение Т>0.
0
х

19.

Основные характеристики
функций
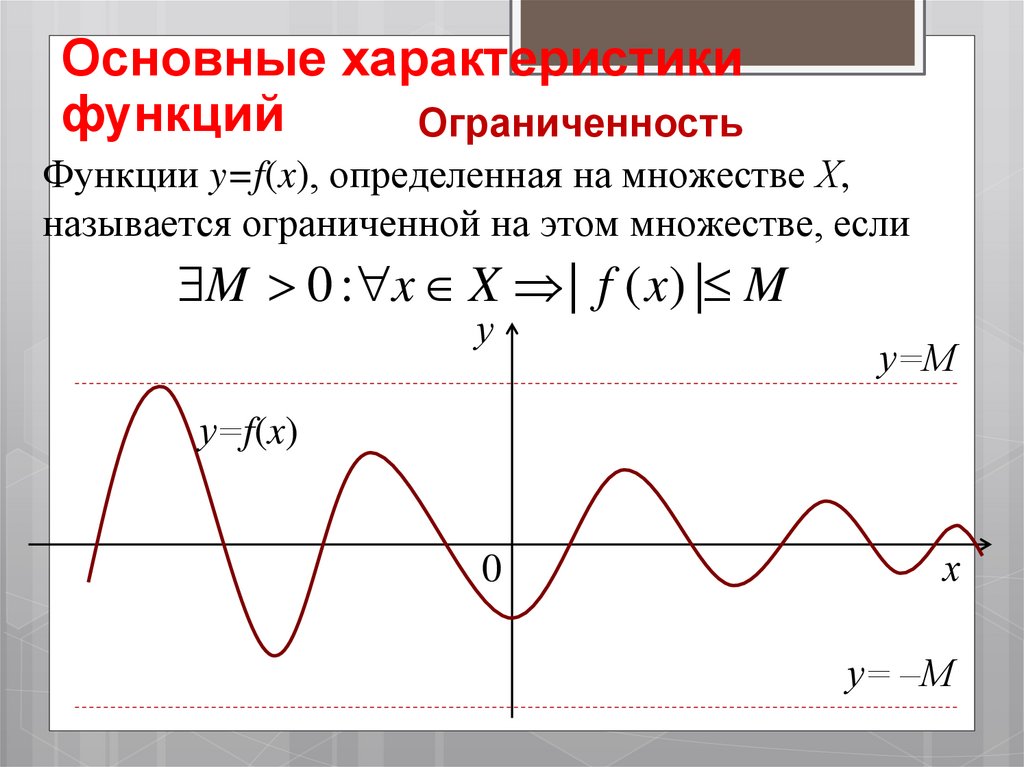
Ограниченность
Функции y=f(x), определенная на множестве Х,
называется ограниченной на этом множестве, если
M 0 : x X | f ( x) | M
у
у=М
у=f(x)
0
х
у= –М

20.

Основные характеристики
функций
Монотонность
Функции y=f(x), определенная на множестве Х,
является
x1 , x2 X : x1 x2
возрастающей
убывающей
f ( x1 ) f ( x2 )
f ( x1 ) f ( x2 )
строго монотонные функции
неубывающией
невозрастающей
f ( x1 ) f ( x2 )
f ( x1 ) f ( x2 )
монотонные функции

21. Сложная функция (функция от функции или суперпозиция функций)

g: X D
f : D Y f (g) : X Y
y f (u ), u g ( x) y f ( g ( x))
промежуточный
аргумент
сложная функция
y f1 ( f 2 ( f 3 (...( f n ( x))...)))
y sin x
2
y sin u
y sin x (sin x)
2
2
y u
u x
2
2
u sin x

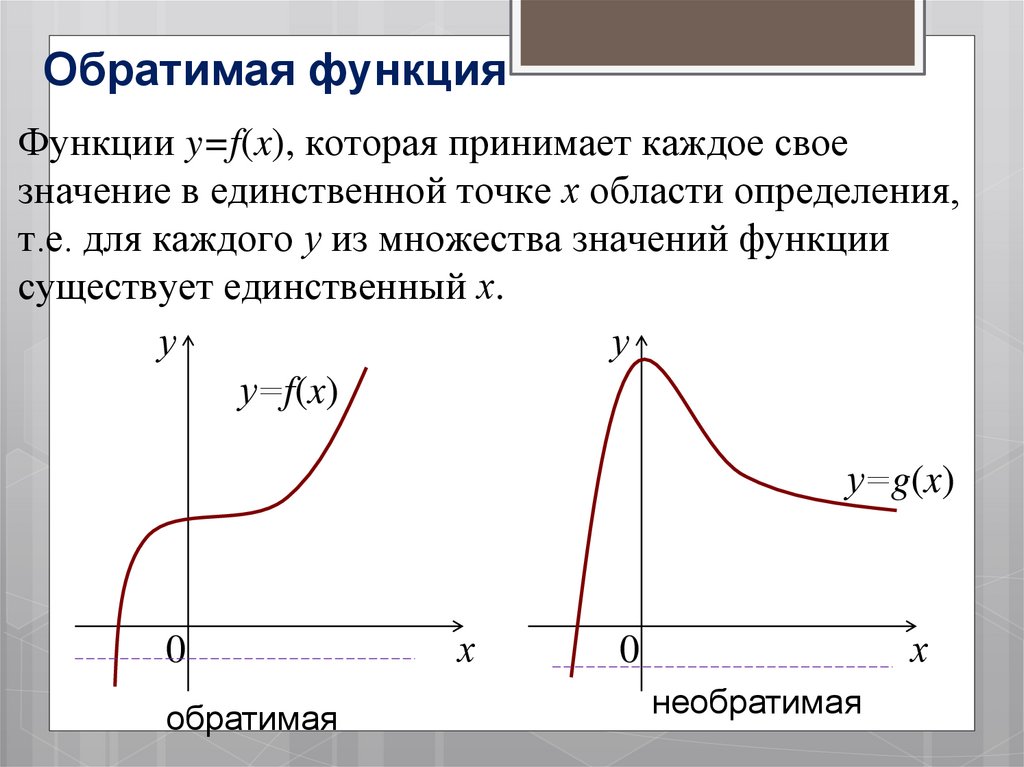
22. Обратимая функция

Функции y=f(x), которая принимает каждое свое
значение в единственной точке х области определения,
т.е. для каждого у из множества значений функции
существует единственный х.
у
у
у=f(x)
у=g(x)
0
обратимая
х
х
0
необратимая

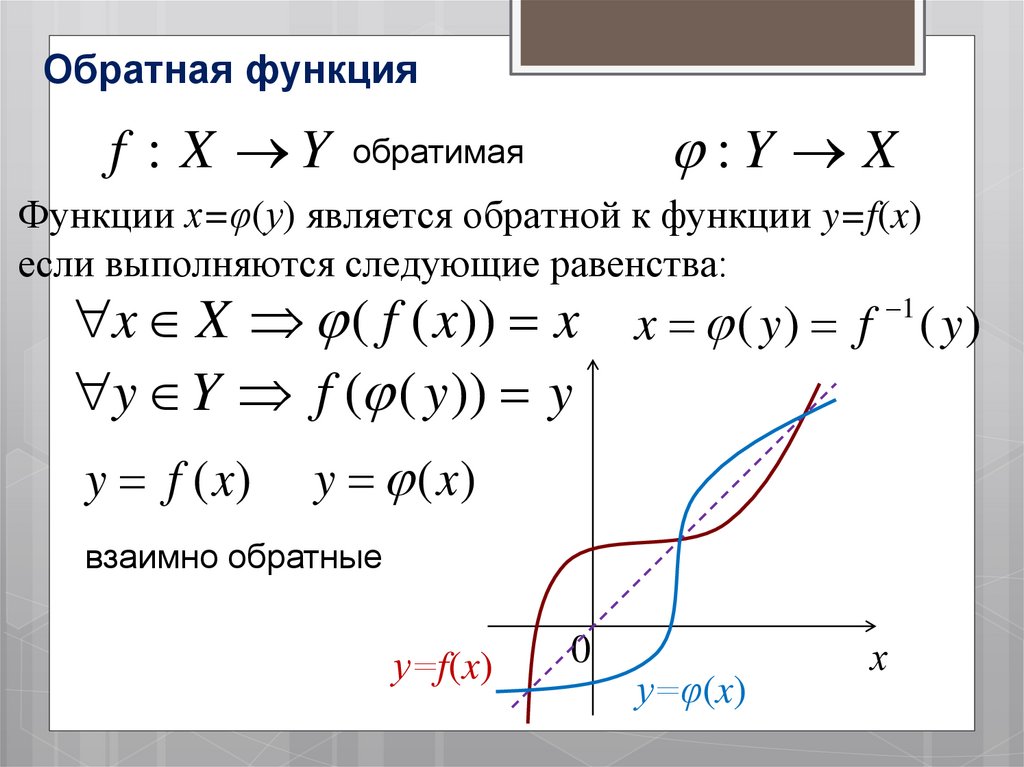
23. Обратная функция

:Y X
f : X Y обратимая
Функции х=φ(у) является обратной к функции y=f(x)
если выполняются следующие равенства:
x X ( f ( x)) x
y Y f ( ( y )) y
y f (x)
x ( y) f ( y)
1
y (x)
взаимно обратные
у=f(x)
0
у=φ(x)
х

24. Основные (простейшие) элементарные функции

y x , R
n N Dom( f ) R параболы порядка п
n Dom( f ) R \ {0} гиперболы порядка п
1
корень
Dom( f ) : x 0 арифметический
степени п
n
Степенная функция
m
Dom( f ) : x 0
n
y x
n
m

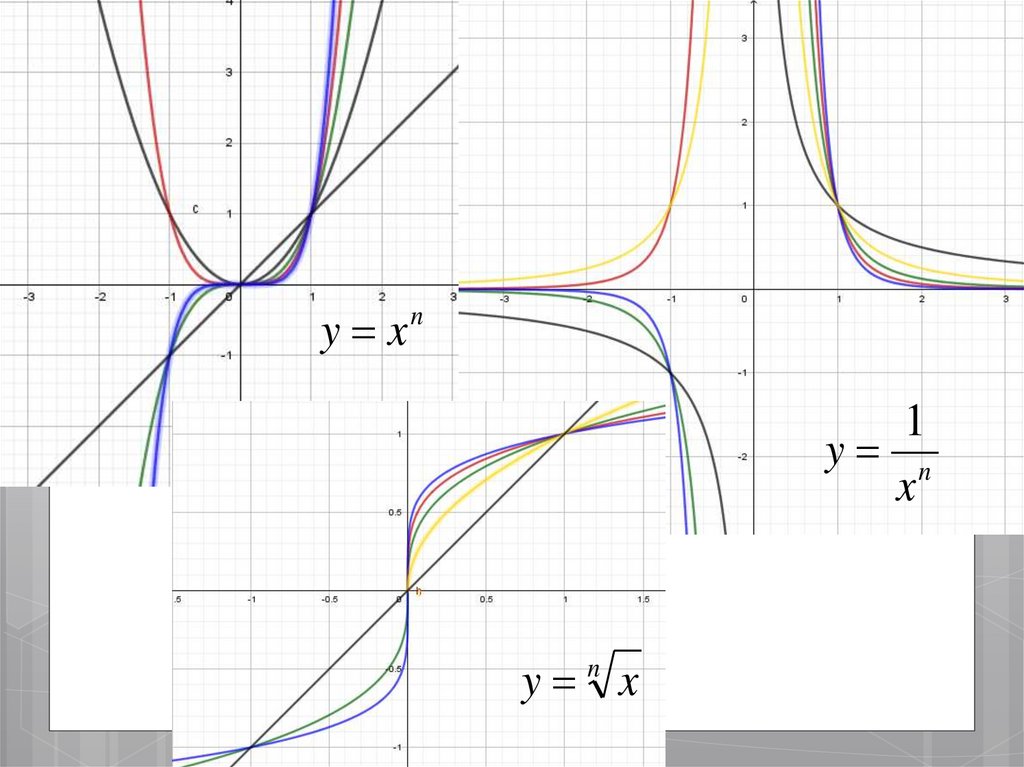
25.

y xn
1
y n
x
y n x

26. Основные (простейшие) элементарные функции

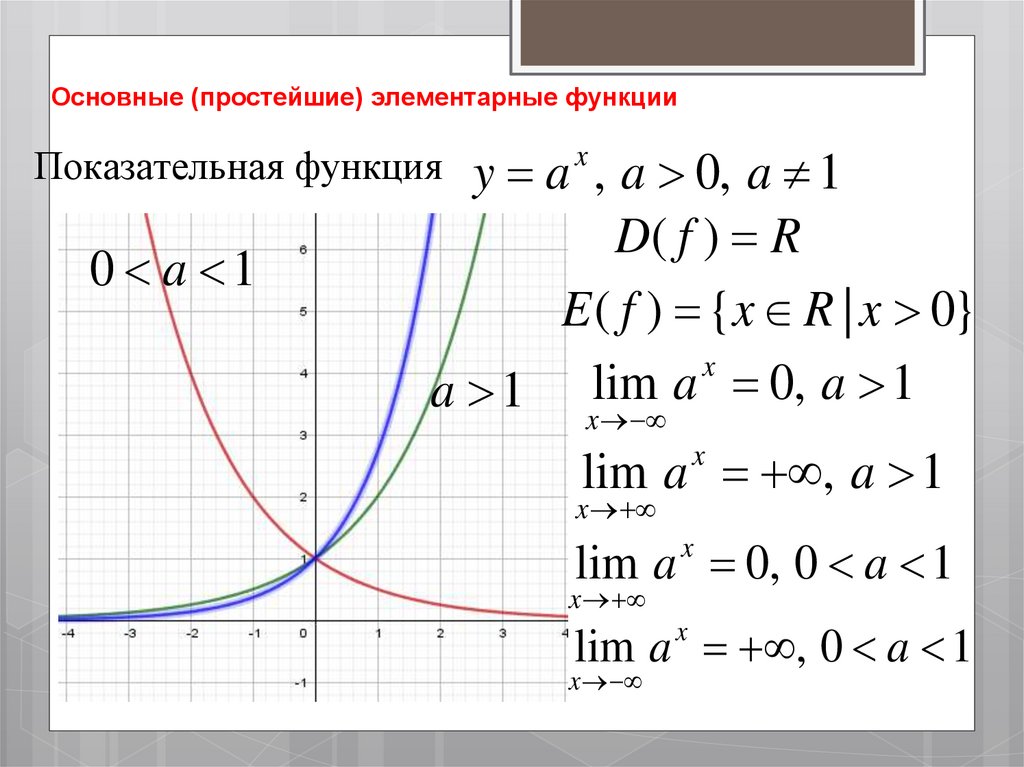
y a , a 0, a 1
D( f ) R
E ( f ) {x R | x 0}
x
a 1 lim a 0, a 1
Показательная функция
0 a 1
x
x
lim a , a 1
x
x
lim a 0, 0 a 1
x
x
lim a , 0 a 1
x
x

27. Основные (простейшие) элементарные функции

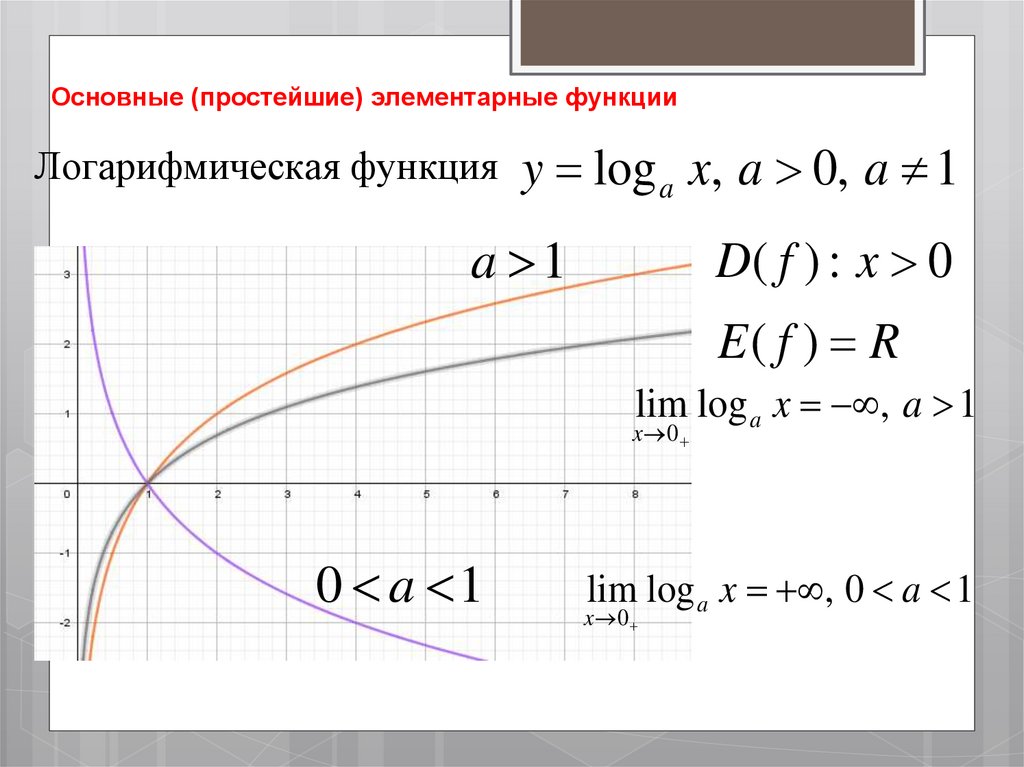
Логарифмическая функция y log a x, a 0, a 1
a 1
D( f ) : x 0
E( f ) R
lim log a x , a 1
x 0
0 a 1
lim log a x , 0 a 1
x 0

28. Основные (простейшие) элементарные функции

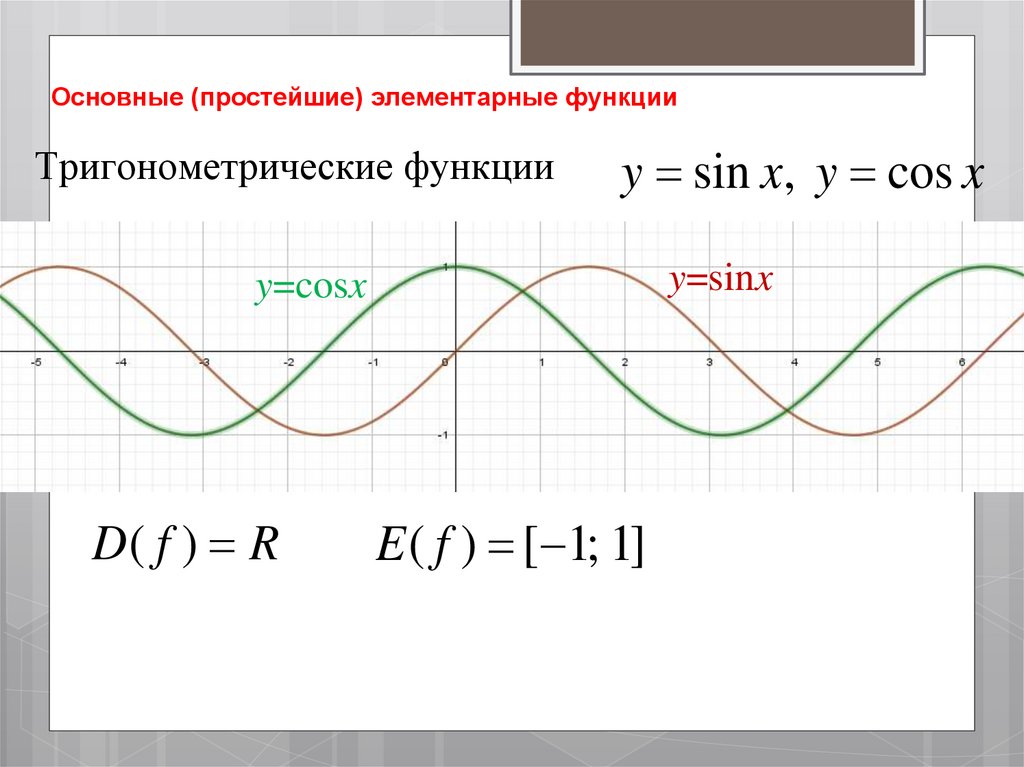
Тригонометрические функции
y sin x, y cos x
y=sinx
y=cosx
D( f ) R
E ( f ) [ 1; 1]

29. Основные (простейшие) элементарные функции

Тригонометрические функции
y tgx, y ctgx
y=tgx
E( f ) R
D(tgx) :
x k , k Z
2
D(сtgx) :
x k , k Z
y=ctgx

30. Основные (простейшие) элементарные функции

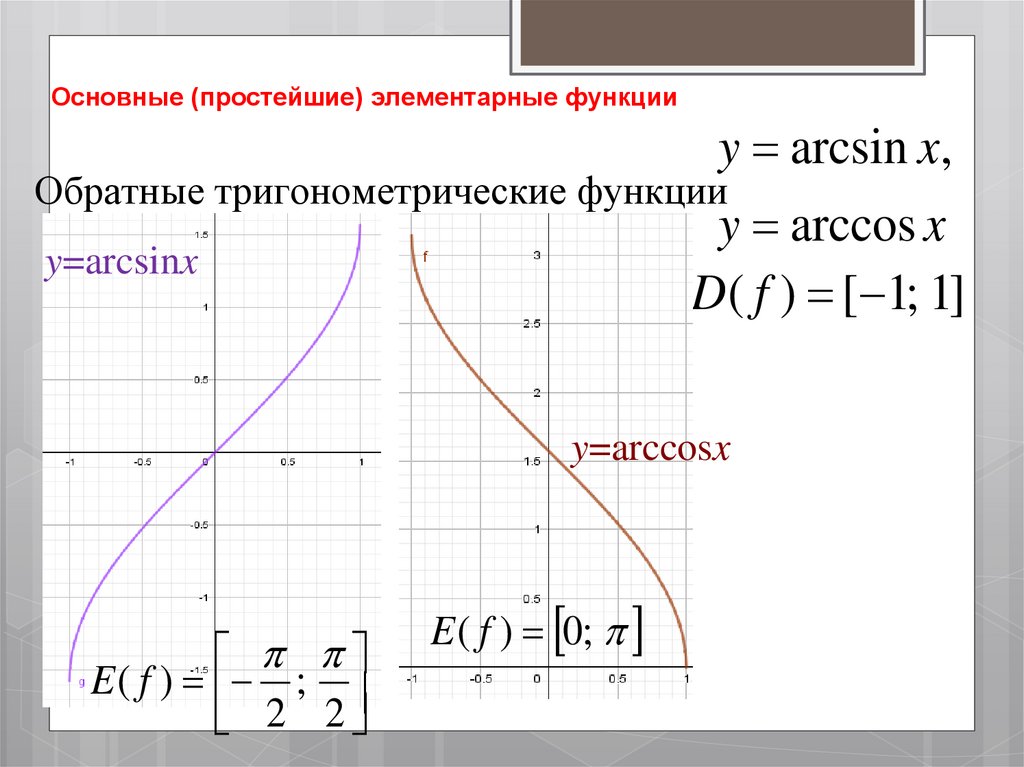
y arcsin x,
Обратные тригонометрические функции
y arccos x
y=arcsinx
D( f ) [ 1; 1]
y=arccosx
E ( f ) ;
2 2
E ( f ) 0;

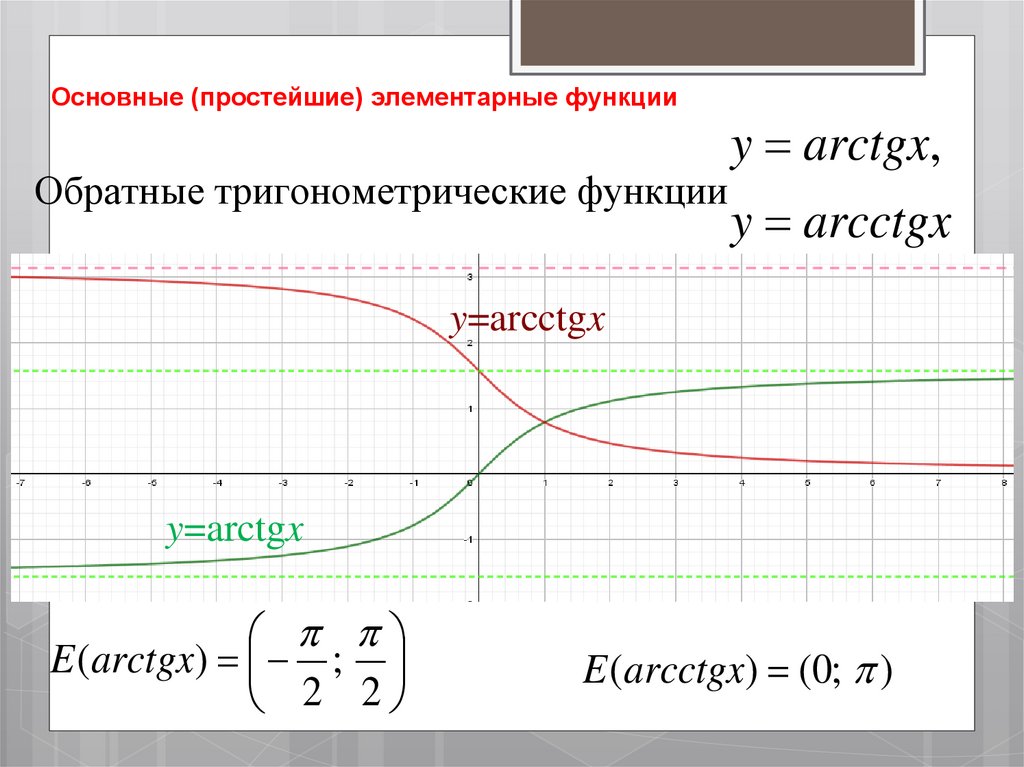
31. Основные (простейшие) элементарные функции

y arctgx,
Обратные тригонометрические функции
y arcctgx
D
(
f
)
R
y=arcctgx
y=arctgx
E (arctgx) ;
2 2
E (arcctgx) (0; )

32.

Элементарные функции
Функции, задаваемые одной формулой,
составленной из основных элементарных
функций и постоянных с помощью конечного
числа арифметических операций и операций
взятия функции от функции.
y log 2
x 2
x 2 1 y x arcsin 3 sin 2 (ln x ) Элементарные
2
3
x
x 8
функции
x, x 0,
y | x 2 | y x y
2
1
x
,x 0
2 n 1
x3 x5
x
y x ... ( 1) n
...
2! 4!
(2n)!
Неэлементарные
функции