Бесконечно малые и бесконечно большие функции. Замечательные пределы. Лекция 9

1.

Лекция № 9. Бесконечно малые и
бесконечно большие функции.
Замечательные пределы
1. Бесконечно большие функции, их связь с
бесконечно малыми функциями.
2. Замечательные пределы.
3. Сравнение бесконечно малых функций.
Эквивалентные бесконечно малые функции.
4. Раскрытие неопределенностей.

2.

1. Бесконечно большие функции, их
связь с бесконечно малыми функциями.
Определение 1. Функция f(x) называется
бесконечно большой в точке x0, если для
любого N существует такое число >0, что
для любого х, удовлетворяющего условию |x–
x0| следует |f(x)|>N.

3.

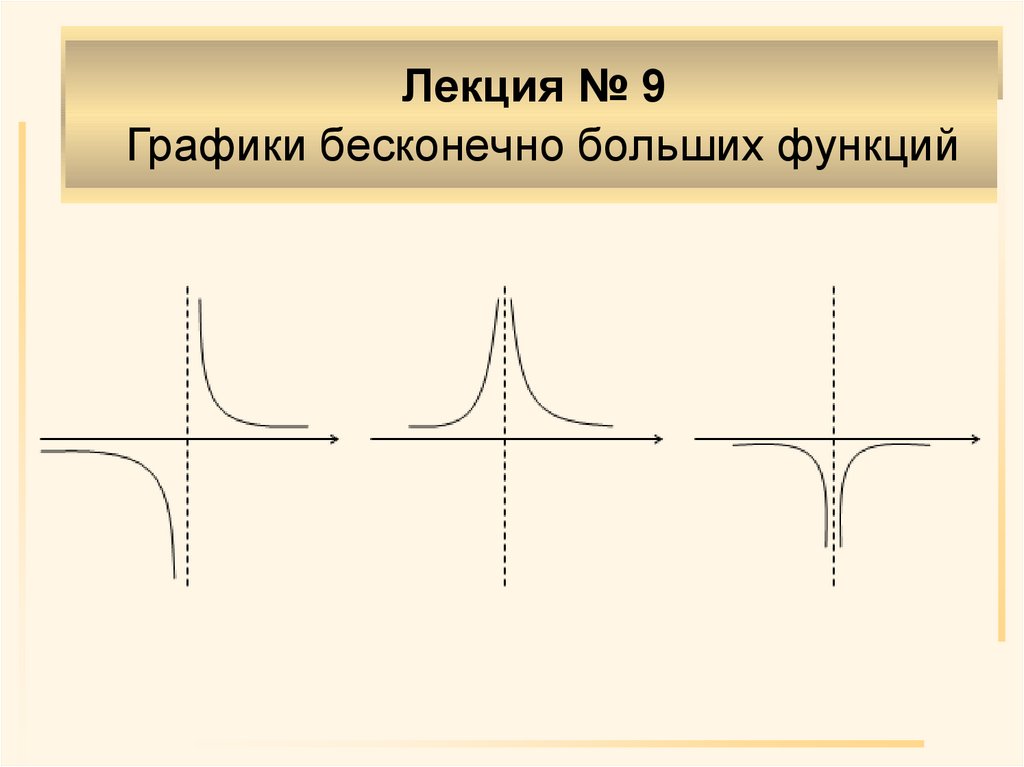
Лекция № 9
Графики бесконечно больших функций

4.

Теорема 1.
Если f(x) – бесконечно большая величина,
то
1
f ( x)
– бесконечно малая величина; если
f(x) – бесконечно малая величина и f(x) 0, то
1
f ( x) – бесконечно большая величина.

5.

Пример 1.
f(x)=x2 – бесконечно малая величина при
х 0;
1
2
х 0. x
– бесконечно большая величина при

6.

Свойства бесконечно больших функций
Свойство 1. Сумма конечного числа
бесконечно больших функций при х х0 тоже
бесконечно большая функция при х х0.

7.

Свойство 2.
Произведение конечного числа бесконечно
больших функций при х х0 тоже бесконечно
большая функция при х х0.

8.

Свойство 3.
Произведение бесконечно большой функции
при х х0 на функцию, имеющую предел,
отличный от нуля, а следовательно, и
произведения бесконечно большой функции на
постоянную, не равную нулю, являются
бесконечно большой функцией при х х0.

9.

2. Замечательные пределы
Первый замечательный предел
sin x
lim
1
x 0 x

10.

Геометрическая интерпретация
АОВ = х
S AOB Sсект. АОВ S AOC .

11.

Доказательство замечательного предела
sinx < x < tgx
x
1
1
.
sin x cos x
sin x
cos x
1,
x
sin x
lim
1.
x 0 x
при 0 < x <
, sinx >0
2

12.

Следствия из первого замечательного предела
sin kx
sin kx
1. lim
k lim
k 1 k.
x 0
kx 0 kx
x
tgkx
sin kx 1
lim
k 1 k.
2. lim
x 0 x
x 0
x coskx
sin kx
sin kx x
1 k
lim
k .
3. lim
x 0 sin mx
x 0
x sin mx
m m

13.

tgkx
tgkx x
k
4. lim
lim
.
x 0 tgmx
x 0 x tgmx
m
arcsin x
y
5. lim
lim
1, где y=arcsinx.
x 0
y 0 sin y
x
arctgx
y
lim
1, где y=arctgx.
6. lim
x 0
y 0 tgy
x

14.

Второй замечательный предел
n
1
lim 1 =е=2,71…
n
n

15.

Следствия из второго замечательного предела
ln( 1 x )
1.
1. lim
x 0
x
ax 1
x
ln a, где a > 0, y=a –1.
2. lim
x 0
x
e 1
3. lim
ln e 1.
x 0
x
x

16.

3. Сравнение бесконечно малых функций.
Эквивалентные бесконечно малые функции.
При (х)→0 справедливы следующие
соотношения эквивалентности

17.

Эквивалентные б.м.
величины

18.

tg5 x
Пример. Найти предел lim
.
x 0 sin 7 x
3
x
Пример. Найти предел lim
.
x 0 1 cos x

19.

4. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
0
1. Неопределенность типа
0
Пусть lim f ( x) 0 , lim g ( x) 0 .
x x0
x x0
f ( x)
Предел lim
называют
x x0 g ( x )
0
неопределенностью типа
.
0

20.

x 6x 8
Пример. Найти предел lim
.
x 2 x 2 8 x 12
2

21.

2. Неопределенность типа
Пусть lim f ( x) , lim g ( x) .
x x0
Предел lim f ( x)
x x0 g ( x )
x x0
называют
неопределенностью типа
.

22.

3. Неопределенность типа 0
Пусть lim f ( x) 0 , lim g ( x) .
x x0
Предел
x x0
lim f ( x) g ( x)
x x0
называют
неопределенностью типа 0 .

23.

4. Неопределенность типа –
Пусть lim f ( x) , lim g ( x) .
x x0
Предел
x x0
lim ( f ( x) g ( x))
x x0
неопределенностью типа – .
называют

24.

5. Показательно-степенные
неопределенности
Показательно-степенные неопределенности
00, 0, 1 сводятся к неопределенности 0
следующим образом:
.
f ( x )
g ( x)
e
g ( x ) ln f ( x )
.

25.

Литература
1. М. Л. Краснов, А. И. Киселев, Г. И.
Макаренко, Е. В. Шикин, В. И. Заляпин
Вся высшая математика. Том 1. Учебник.
(линейная алгебра и аналитическая
геометрия, введение в математический
анализ). -М.: Едиториал УРСС, 2012 – [1],
с. 206-209; 215-216; 225-228.