Similar presentations:
Бесконечно малые функции
1.
Бесконечно малые функцииПолезно иметь в виду эквивалентность следующих бесконечно
малых при x 0
m
sin x ~ x;
e x 1 ~ x;
1 x 1 ~ mx
;
x
tgx ~ x;
a 1 ~ x ln a;
x2
1 cos x ~ .
arcsin x ~ x; ln x 1 ~ x;
2
arctg x ~ x; loga x 1 ~ x loga e;
sin x
0
lim
x 0 4
0
1 x 1
x
lim
4
x 0
0.25 x
sin x ~ x
1
1
1 x 4 1 ~ x
4
2.
Бесконечно малые функцииФункция y = f(x) называется бесконечно малой при
x x0
( x )
если
lim f ( x ) 0
x x0
x
Бесконечно малые функции часто называют бесконечно малыми
величинами; обозначают обычно греческими буквами α, β и т. д.
Например:
sin x 0
lim
x 0
( x ) sin x - бесконечно малая функция при x 0
Теорема
Если функция y = f(x) имеет предел, равный А, то ее можно
представить как сумму числа А и бесконечно малой функции α(x)
lim
f
(
x
)
A
x x
0
f ( x ) A ( x )
3.
Бесконечно малые функцииСравнение бесконечно малых
Пусть α(х), β(х) – бесконечно малые функции
Если
( x )
lim
0
x x0
( x )
то говорят, что α(х) является бесконечно малой высшего
порядка по сравнению с β(х) : o( )
Если
( x )
lim
m
x x0
( x )
( m 0)
то говорят, что α(х) и β(х) – бесконечно малые одного и того
же порядка.
Если
( x )
lim
1
x x0
( x )
то α(х) и β(х) – эквивалентные
бесконечно малые ~
4.
msin x ~ x;
e x 1 ~ x;
1 x 1 ~ mx
;
x
tgx ~ x;
a 1 ~ x ln a;
x2
1 cos x ~ .
arcsin x ~ x; ln x 1 ~ x;
2
arctg x ~ x; loga x 1 ~ x loga e;
5.
Односторонниепределы
Точки разрыва
функции
Непрерывность
функции в точке
Непрерывность
функции в
интервале и на
отрезке
6.
Точки разрыва функцииТочки, в которых нарушается непрерывность функции, называется
точками разрыва функции.
Если x = x0 – точка разрыва функции, то в ней не выполняется по
крайней мере одно из условий первого определения
непрерывности, а именно:
y
1
Функция f(x) определена в
окрестности точки х0 , но
не определена в самой
точке х0 :
Функция
1
y
x 2
0
2
не определена в точке х = 2 , но определена в любой
окрестности этой точки, поэтому х = 2 - точка разрыва.
х
7.
Точки разрыва функции2
Функция f(x) определена в точке х0 и в ее окрестности, но не
существует предела f(x) при x x 0
Функция
x 1; x 2
y
2 x; x 2
определена в точке х = 2 , но но не имеет предела при
lim
f
(
x
)
1
x 2 0
y
x 2:
lim
f
(
x
)
0
x 2 0
lim f ( x ) xlim
f (x)
2 0
x 2 0
0
2
х
lim
f
(
x
)
x 2
не существует, значит
х = 2 - точка разрыва
8.
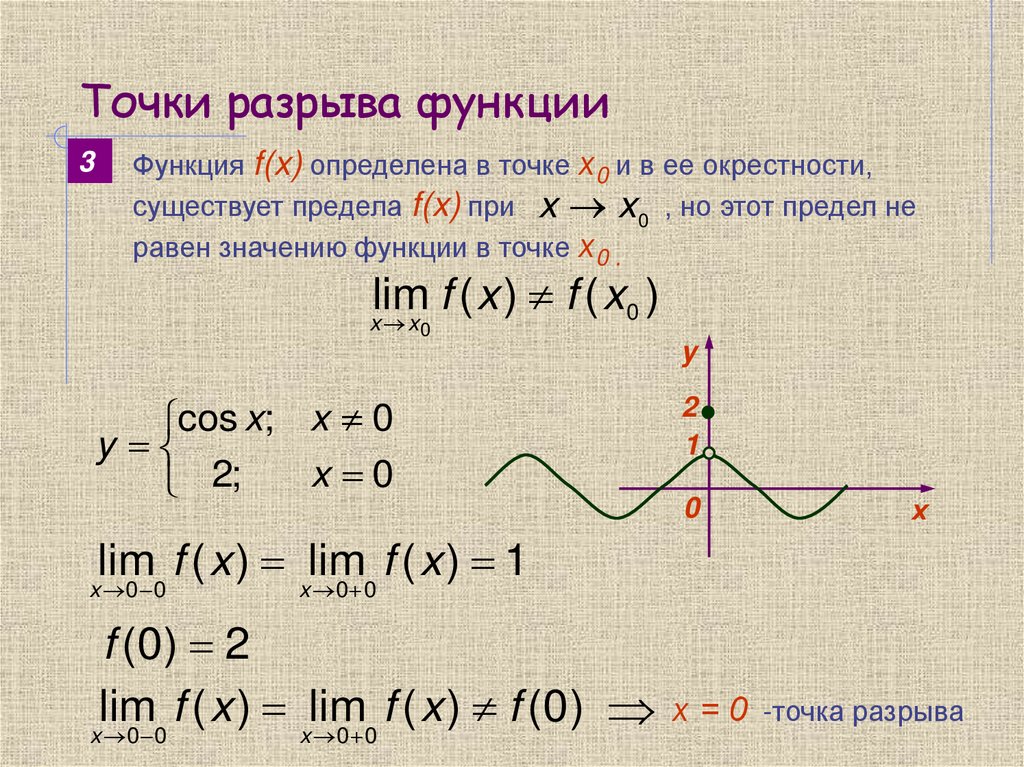
Точки разрыва функции3
Функция f(x) определена в точке х0 и в ее окрестности,
существует предела f(x) при x x 0 , но этот предел не
равен значению функции в точке х0 .
lim
f
(
x
)
f
(
x
)
0
x x
0
y
cos x; x 0
y
x 0
2;
2
1
0
х
lim f ( x ) xlim
f (x) 1
0 0
x 0 0
f (0 ) 2
х = 0 -точка разрыва
lim
f
(
x
)
lim
f
(
x
)
f
(
0
)
x 0 0
x 0 0
9.
Непрерывность функции в интервале ина отрезке.
Функция y = f(х) называется непрерывной на интервале (a; b),
если она непрерывна в каждой точке этого интервала.
Функция y = f(х) называется непрерывной на отрезке [a; b], если
она непрерывна на интервале (a; b), и в точке x = a непрерывна
справа:
lim
f
(
x
)
f
(
a
)
x a 0
а в точке x = b непрерывна слева:
lim
f
(
x
)
f
(
b
)
x b 0
10.
Точки разрыва функцииТочка разрыва х0 называется точкой разрыва 1 рода функции
f(x) , если в этой точке существуют конечные пределы слева и
справа:
lim f ( x ) A
lim
f
(
x
)
A
1
x x 0
0
x x0 0
2
При этом:
а) если A1 A2 , то х0 - точка устранимого разрыва
(в примере 3: х = 0 – точка устранимого разрыва 1 рода)
б) если A1 A2 , то х0 - точка конечного разрыва
Величину A1 A2 называют скачком функции в точке
разрыва 1 рода.
( в примере 2: х = 2 – точка разрыва 1 рода, скачек функции
равен: 1 0 1)
11.
Точки разрыва функцииТочка разрыва х0 называется точкой разрыва 2 рода функции
f(x) , если по крайней мере один из односторонних пределов не
существует или равен бесконечности.
В примере 1:
1
y
x 2
1
lim
x 2 0
x 2
1
lim
x 2 0
x 2
х = 2 – точка разрыва 2 рода.



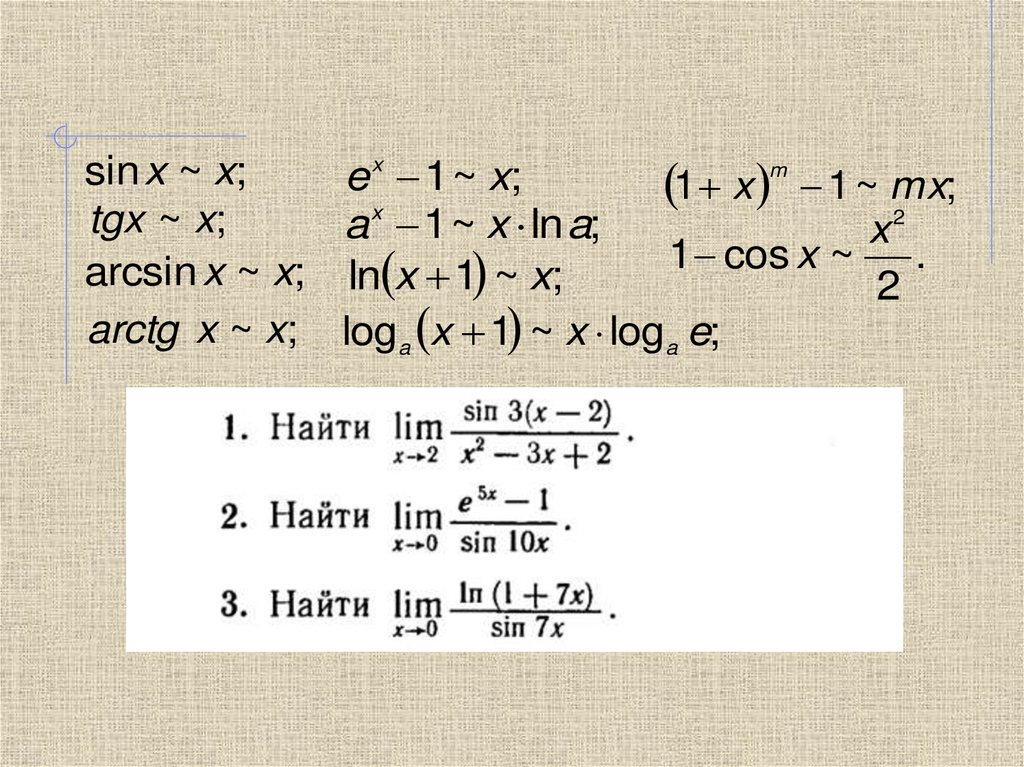








 mathematics
mathematics








