Математические и имитационные модели информационных потоков на предприятии

1.

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Пермский национальный исследовательский политехнический университет (ПНИПУ)
Факультет: Электротехнический (ЭТФ)
Направление: Информатика и вычислительная техника (ИВТ)
Профиль: Автоматизация управления бизнес-процессами и финансами (АУБПиФм)
Кафедра информационных технологий и автоматизированных систем (ИТАС)
Зав. кафедрой: д-р экон. наук, проф.
Файзрахманов Р.А.2015 г.
КУРСОВОЙ ПРОЕКТ
по дисциплине: «Математические методы теории систем»
на тему
«Математические и имитационные модели информационных потоков на предприятии»
Студент: Ушахин Никита Дмитриевич
Группа:
АСУ3-15-1м
Руководитель
работы:
Пермь — 2015
курсовой д-р экон.наук, проф. Файзрахманов
Р.А.
1

2.

Введение
• Цель курсового проекта: Создать математическую и
имитационную модель многофазной системы массового
обслуживания на примере документооборота.
• Задачи курсового проекта:
- Изучить теорию массового обслуживания;
- Рассмотреть основы математического моделирования;
- Создать математическую модель документооборота но
основе теории массового обслуживания;
- Создать имитационную модель документооборота но
основе теории массового обслуживания;
2

3.

Математическое моделирование
• Математическое моделирование – это
теоретико-экспериментальный метод
позновательно-созидательной
деятельности, метод исследования и
объяснения явлений, процессов и систем
(объектов-оригиналов) на основе создания
новых объектов – математических моделей
3

4.

Системы массового обслуживания
• Системы массового обслуживания (СМО)—
это такие системы, в которые в случайные
моменты времени поступают заявки на
обслуживание, при этом поступившие
заявки обслуживаются с помощью
имеющихся в распоряжении системы
каналов обслуживания
4

5.

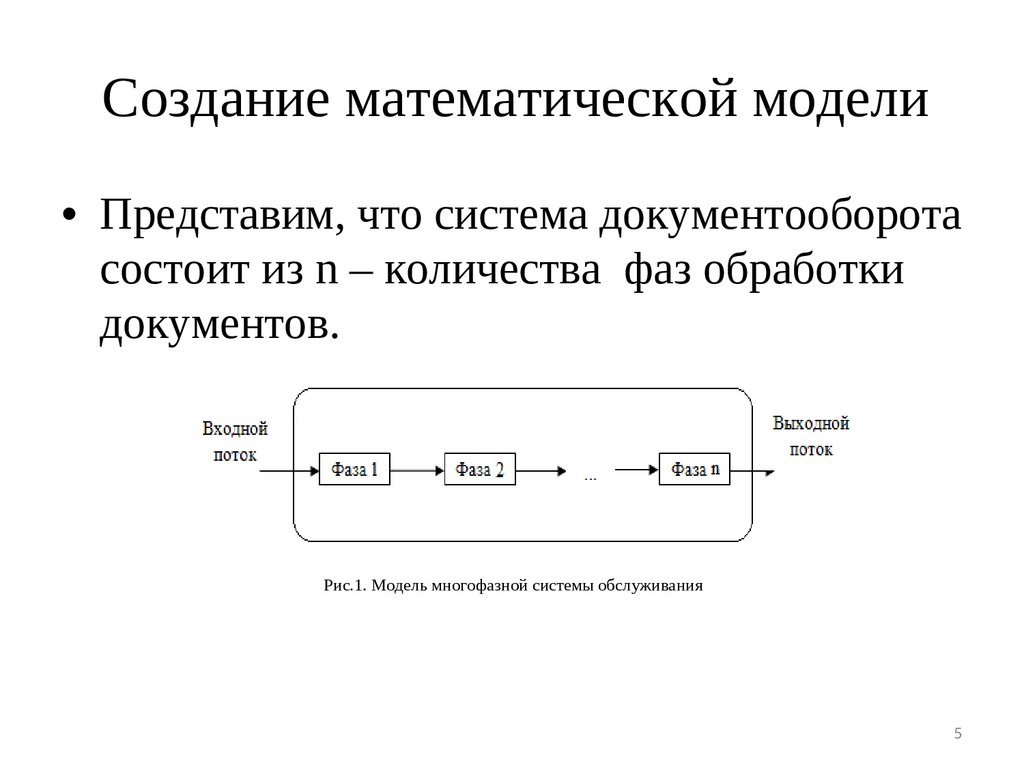
Создание математической модели
• Представим, что система документооборота
состоит из n – количества фаз обработки
документов.
Рис.1. Модель многофазной системы обслуживания
5

6.

Создание математической модели
• Предполагается, что при наличии заявки в
очереди на входе в прибор, при уходе неё
обработанной заявки, освободившееся
место тотчас занимается заявкой, стоящей в
очереди.
6

7.

Создание математической модели
• Пути, по которым идут и обрабатываются
документы представлена на рисунке
Рис.2. Пути обработки данных в многофазной системы обслуживания
7

8.

Создание математической модели
• Множество состояний многофазной системы
обслуживания будет следующим: S0 = (r1,t1;
r2,t2; … rn,tn); S1 = (r1,t1; r2,t2; … rn,tn); … Sn =
(r1,t1; r2,t2; … rn,tn);
где r1 = 0, r2 = 1, rn = 0;1. t1 = 0, t2 = 1, tn = 0;1.
Sn – количество возможных состояний
системы
8

9.

Создание математической модели
На основе множеств состояний многофазной системы построим граф
переходов состояний системы
Рис.3. Граф переходных состояний многофазной системы обслуживания
9

10.

Создание математической модели
• Исходя из полученного графа составим
систему уравнений Колмогорова
Рис.4. Система уравнений Колмогорова
10

11.

Создание математической модели
• Рассмотрим пример движения и обработки
документов в 2-х фазной системе
Рис.5. Путь движения документа в 2-х фазной системе
11

12.

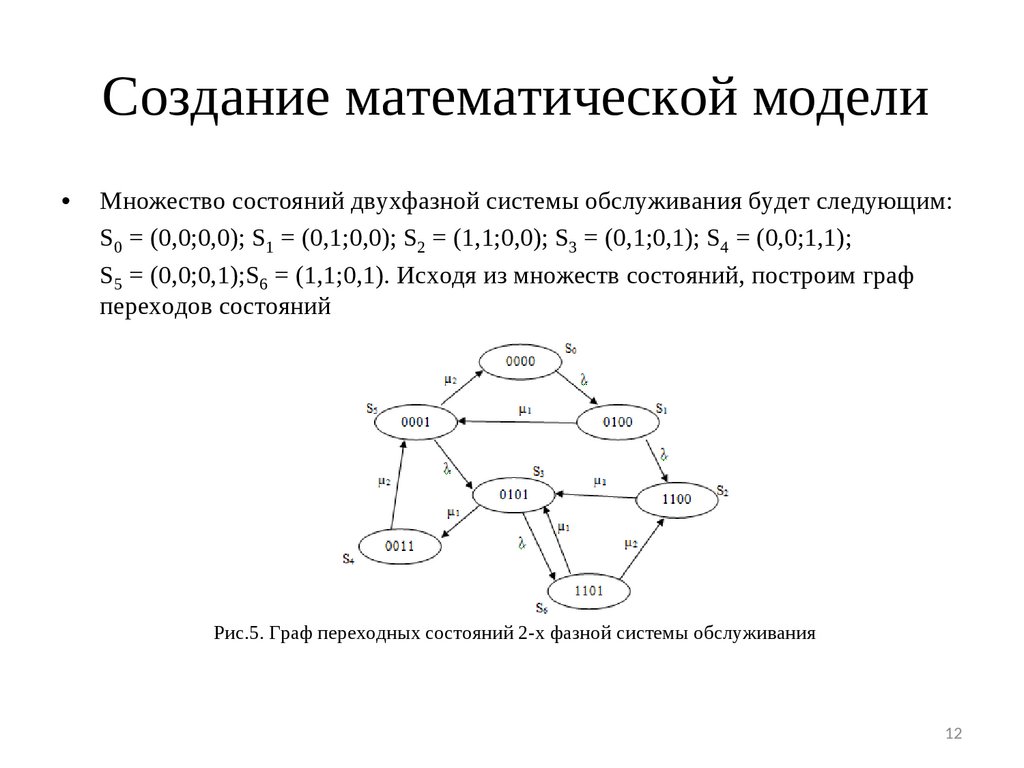
Создание математической модели
Множество состояний двухфазной системы обслуживания будет следующим:
S0 = (0,0;0,0); S1 = (0,1;0,0); S2 = (1,1;0,0); S3 = (0,1;0,1); S4 = (0,0;1,1);
S5 = (0,0;0,1);S6 = (1,1;0,1). Исходя из множеств состояний, построим граф
переходов состояний
Рис.5. Граф переходных состояний 2-х фазной системы обслуживания
12

13.

Создание математической модели
• Исходя из графа составим систему
дифференциальных уравнений
Рис.6. Система дифференциальных уравнений
13

14.

Создание математической модели
• Решим пример методом Гаусса, используя
следующие переменные: λ = 1, µ1 = 1, µ2 = 2.
• Решив систему уравнений получим p0 = 10%,
p1 = 15%, p2 = 29%, p3 = 21%, p4 = 10%, p5 =
5%, p6 = 7%. Т.е. в предельном, стационарном
режиме система S в среднем 10% времени
будет находится в состоянии S0, 15% - в
состоянии S1, 29% - в состоянии S2, 21% - в
состоянии S3, 10% - в состоянии S4, 5% - в
состоянии S5, 7% - в состоянии S6.
14

15.

Создание имитационной модели
• Для имитационного решения проблемы мы
воспользуемся инженерной программой
MatLab. В MatLab нам понадобится
библиотека SimEvents. Она предназначена
для моделирования систем с дискретными
состояниями, в том числе моделирования
систем массового обслуживания.
15

16.

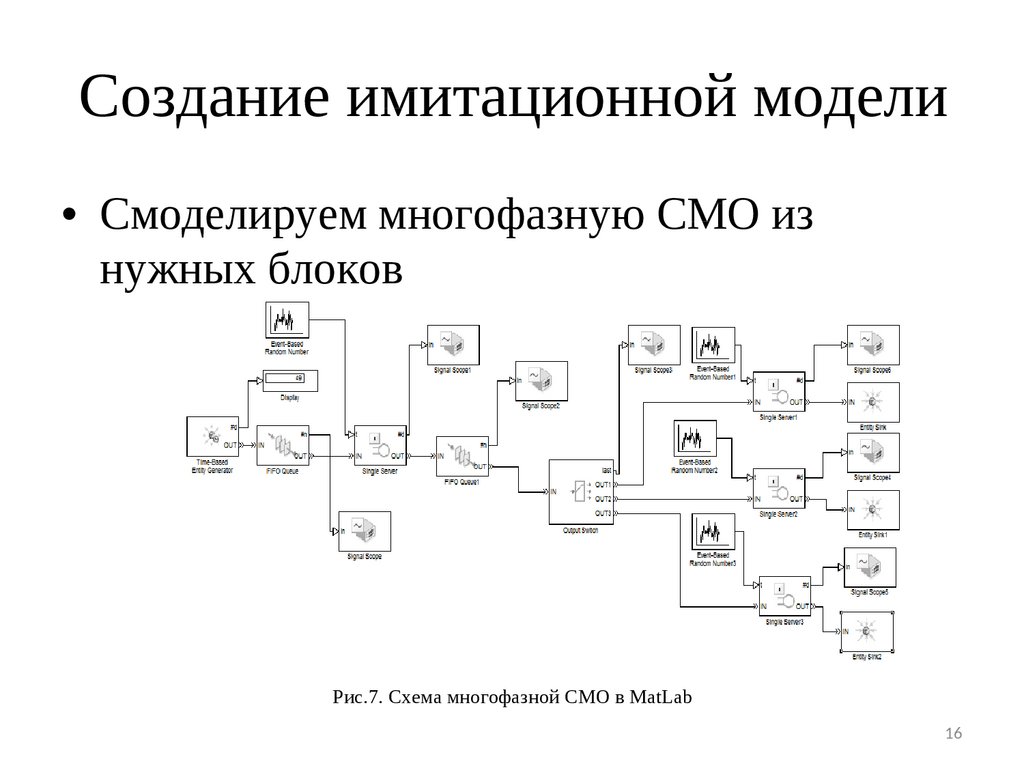
Создание имитационной модели
• Смоделируем многофазную СМО из
нужных блоков
Рис.7. Схема многофазной СМО в MatLab
16

17.

Создание имитационной модели
• Заявки на обслуживание прибывают в
систему с интенсивностью 0,06 (1 заявка в
17 минут). Среднее время обслуживания
заявок сервером составляет 20 минут.
Время моделирования 480.
17

18.

Создание имитационной модели
При запуске были сняты с блоков Signal Scope следующие результаты:
Signal Scope. Из этого графика следует, что не все появляющиеся
заявки сразу поступают на обслуживание, имеются заявки, которые
накапливаются в очереди (Рис.8).
Рис.8. Процедура прохождения заявок через накопитель
18

19.

Создание имитационной модели
Signal Scope 1. Блок Signal Scope1 показывает процедуру
обслуживания заявок сервером (Рис. 9).Горизонтальная ось времени
показывает моменты, в которые заявки поступают на вход блока Single
Server.
Рис. 9. Формирование времени обслуживания заявок на входе блока Single Server
19

20.

Создание имитационной модели
Signal Scope 2. Блок Signal Scope 2 показывает число заявок,
находящихся в очереди и ожидающих обслуживания.
Рис. 10. Число зававок в очереди
20

21.

Создание имитационной модели
Signal Scope 3. Блок Signal Scope 3 показывает число заявок,
направленных в выходной порт, т. е. на последующее обслуживание в
один из трех серверов Single Server
Рис. 11. Распределение заявок выходным переключателем OutputSwitch
21

22.

Создание имитационной модели
Блоки SignalScope 4, SignalScope 5, SignalScope 6 показывают
процедуру обслуживания заявок серверами SingleServer 1,
SingleServer 2, SingleServer 3, соответственно.
Рис. 12.
Рис. 13.
Рис. 14.
22

23.

Заключение
• В первой части были изучены следующие понятия:
Понятие моделирования;
Понятие математическое моделирование;
Понятие имитационное моделирование
• Во
второй
части
курсовой
работы
были
создана
математическая модель потоков документов на предприятии,
используя
теорию
массового
обслуживания.
Создана
имитационная модель потоков документов на предприятии.
Используя для этого Инженерную программу MatLab.
23