1.89M

Category:

informatics

Модели и моделирование. Математическое моделирование

1. Моделирование

1
Моделирование
§ 13. Модели и моделирование
§ 14. Математическое моделирование
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

2. Моделирование

2
Моделирование
§ 13. Модели и моделирование
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

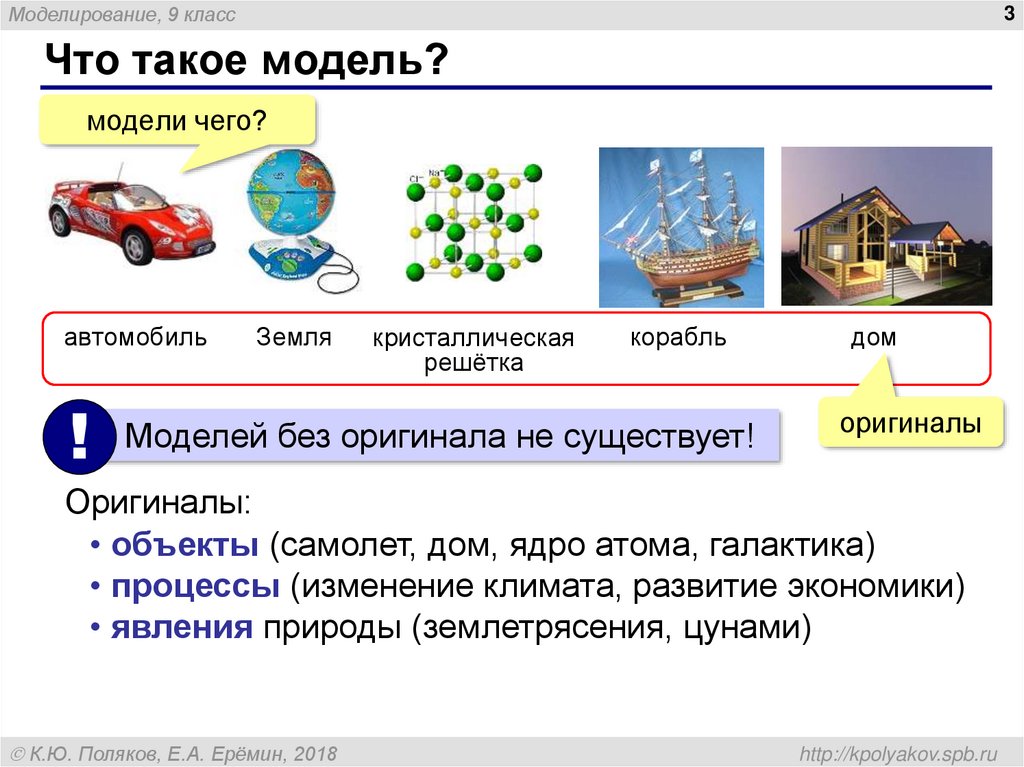
3. Что такое модель?

Моделирование, 9 класс
3
Что такое модель?
модели чего?
автомобиль
!
Земля
кристаллическая
решётка
корабль
Моделей без оригинала не существует!
дом
оригиналы
Оригиналы:
• объекты (самолет, дом, ядро атома, галактика)
• процессы (изменение климата, развитие экономики)
• явления природы (землетрясения, цунами)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

4. Что такое модель?

Моделирование, 9 класс
4
Что такое модель?
?
Зачем нужны модели?
Нужно решить задачу, связанную с оригиналом, но:
• оригинал не существует
- древний Египет
- последствия ядерной войны (Н.Н. Моисеев, 1966)
• исследование оригинала дорого или опасно
- управление ядерным реактором (Чернобыль, 1986)
- испытание нового скафандра для космонавтов
- разработка нового самолета или корабля
• оригинал сложно исследовать
-
Солнечная система, галактика (большие размеры)
атом, нейтрон (маленькие размеры)
процессы в двигателе внутреннего сгорания (очень быстрые)
геологические явления (очень медленные)
• интересуют только отдельные свойства
- проверка краски для фюзеляжа самолета
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

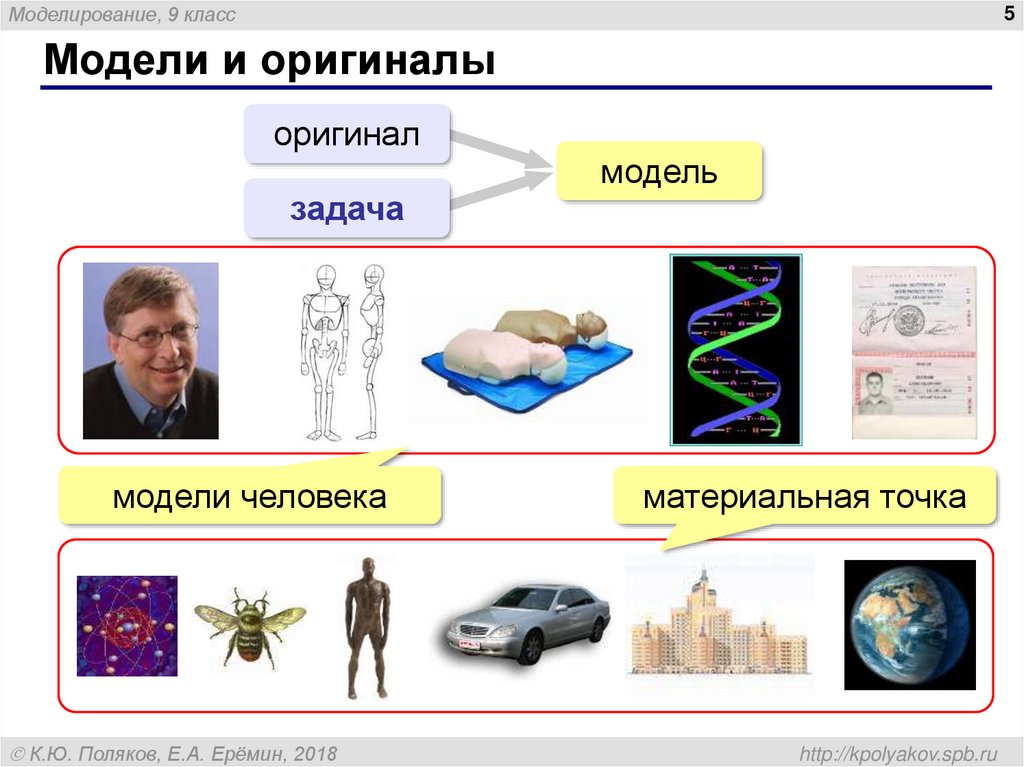
5. Модели и оригиналы

Моделирование, 9 класс
5
Модели и оригиналы
оригинал
задача
модели человека
К.Ю. Поляков, Е.А. Ерёмин, 2018
модель
материальная точка
http://kpolyakov.spb.ru

6. Модели и моделирование

Моделирование, 9 класс
6
Модели и моделирование
Модель – это объект, который обладает существенными
свойствами другого объекта, процесса или явления
(оригинала) и используется вместо него.
Моделирование – это создание и исследование моделей
с целью изучения оригиналов.
Задачи моделирования:
• исследование оригинала
• анализ («что будет, если …»)
• синтез («как сделать, чтобы …»)
• оптимизация («как сделать лучше всего …»)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

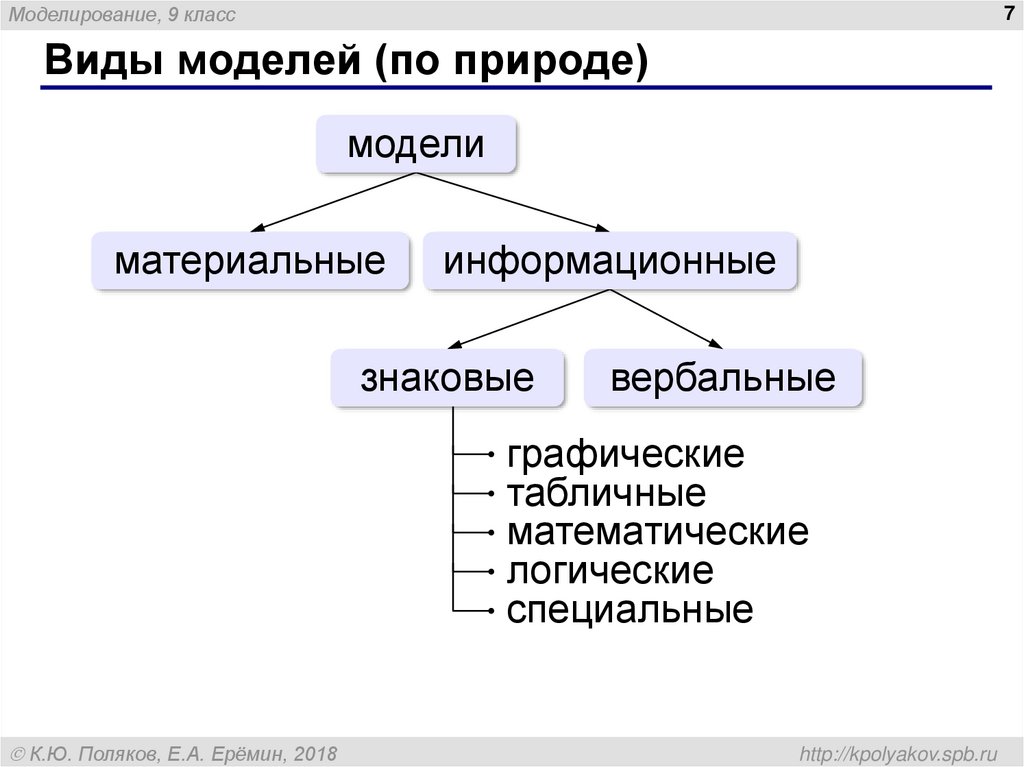
7. Виды моделей (по природе)

Моделирование, 9 класс
7
Виды моделей (по природе)
модели
материальные
информационные
знаковые
вербальные
графические
табличные
математические
логические
специальные
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

8. Виды моделей (по фактору времени)

Моделирование, 9 класс
8
Виды моделей (по фактору времени)
• статические – описывают оригинал в заданный
момент времени
силы, действующие на тело в состоянии покоя
результаты осмотра врача
фотография
…
• динамические
модель движения тела
явления природы (молния, землетрясение, цунами)
история болезни
видеозапись события
…
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

9. Виды динамических моделей

Моделирование, 9 класс
9
Виды динамических моделей
• непрерывные – описывают оригинал в любой момент
времени на заданном интервале
y
y = 2t + 5
t
• дискретные – описывают оригинал только в отдельные
моменты времени (через 1 сек, час, год, …)
yi = 2ti + 5
y
y1 y2 y3
yi = 5yi–1 + 5
y4
y0
t
t0 t1 t2 t3 t4
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

10. Виды моделей (по характеру связей)

Моделирование, 9 класс
10
Виды моделей (по характеру связей)
• детерминированные – при одинаковых исходных
данных всегда получается тот же результат
расчёт по формулам
движение корабля на спокойной воде
…
• вероятностные – учитывают случайность событий
броуновское движение частиц
полета самолёта с учетом ветра
движения корабля на волнении
поведение человека
…
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

11. Имитационные модели

Моделирование, 9 класс
11
Имитационные модели
• нельзя заранее вычислить или предсказать поведение
системы, но можно имитировать её реакцию на внешние
воздействия
• максимальный учет всех факторов
• только численные результаты
!
Задача – найти лучшее решение методом
проб и ошибок (многократные эксперименты)!
Примеры:
• испытания лекарств на мышах, обезьянах, …
• математическое моделирование биологических систем
• модели систем массового обслуживания
• модели процесса обучения
• кросс-программирование
•…
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

12. Игровые модели

Моделирование, 9 класс
12
Игровые модели
Игровые модели учитывают действия противников.
экономические ситуации
военные действия
спортивные игры
тренинги персонала
!
Задача – найти лучший вариант действий в
самом худшем случае!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

13. Адекватность

Моделирование, 9 класс
13
Адекватность
Адекватность – это совпадение существенных свойств
модели и оригинала в данной задаче.
результаты моделирования согласуются с выводами
теории (законы сохранения и т.п.)
X – моделирование
X* - эксперимент
подтверждаются экспериментом
относительная ошибка X
!
X X*
X*
100% < 10%
Адекватность модели можно доказать только
экспериментом!
Модель всегда отличается от оригинала
!
Любая модель адекватна только при
определенных условиях!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

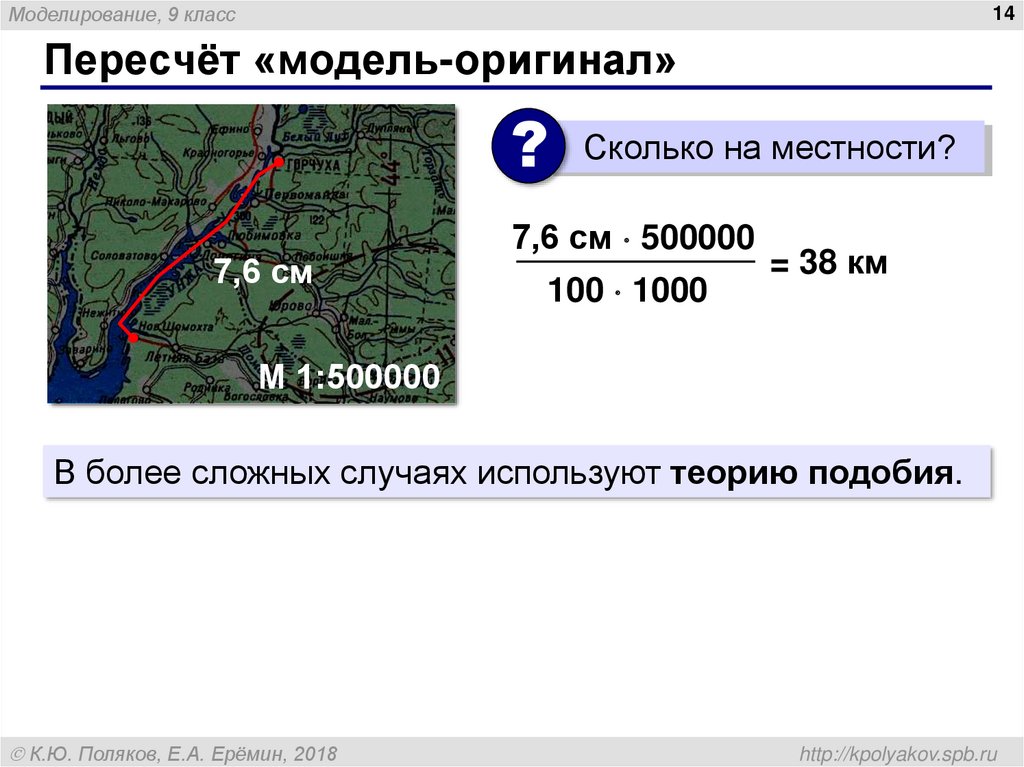
14. Пересчёт «модель-оригинал»

Моделирование, 9 класс
14
Пересчёт «модель-оригинал»
?
7,6 см
Сколько на местности?
7,6 см 500000
100 1000
= 38 км
М 1:500000
В более сложных случаях используют теорию подобия.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

15. Моделирование

15
Моделирование
§ 14. Математическое
моделирование
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

16. I. Постановка задачи

Моделирование, 9 класс
16
I. Постановка задачи
Хорошо поставленная задача:
• описаны все связи между исходными данными и
результатом
• известны все исходные данные
• решение существует
• задача имеет единственное решение
Примеры плохо поставленных задач:
• Уроки в школе начинаются в 830. В 1000 к школе подъехал
красный автомобиль. Определите, когда Шурик выйдет
играть в футбол?
• Мальчик Вася в синей кепке бросает белый мяч со
скоростью 12 м/с. Когда мяч впервые ударится о землю?
• Решить уравнение sin x = 4 (нет решений).
• Найти функцию, которая проходит через точки (0,1) и (1,0)
(бесконечно много решений).
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

17. I. Постановка задачи

Моделирование, 9 класс
17
I. Постановка задачи
Мальчик Вася в синей кепке бросает белый мяч со
скоростью 12 м/с. Когда мяч впервые ударится о землю?
?
Хорошо поставлена?
Допущения:
• Вася бросает мяч вертикально вверх.
• В момент броска мяч находится на высоте 1,5 м.
? Всегда ли есть решение?
? Решение единственно?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

18. II. Разработка математической модели

Моделирование, 9 класс
18
II. Разработка математической модели
1) выделить существенные исходные данные:
• начальная скорость 12 м/с
• бросок вертикально вверх
• ускорение свободного падения 9,81 м/с2
2) построить математическую модель
Графическая модель:
y
v0
h0, v0
исходные данные
?
модель
tп
результаты
Такой модели достаточно?
h0
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

19. II. Разработка математической модели

Моделирование, 9 класс
19
II. Разработка математической модели
Ещё допущения:
• мяч – материальная точка
• нет сопротивления воздуха
Формализация:
h0
v0
t
где
g t
y h0 v0 t
2
– начальная высота
– начальная скорость
– время
Мяч упал:
!
2
g t
0 h0 v0 tn
2
2
n
Связали исходные данные и результат!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

20. III. Тестирование модели

Моделирование, 9 класс
20
III. Тестирование модели
Тестирование – это проверка модели на простых
исходных данных с известным результатом.
g t
y h0 v0 t
2
2
• при t = 0 y = h0 (в начальной точке)
• при v0 = 0 падение вниз
?
Доказывает ли успешное тестирование
правильность модели?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

21. IV. Построение компьютерной модели

Моделирование, 9 класс
21
IV. Построение компьютерной модели
g tn2
0 h0 v0 tn
2
?
алг Полёт
нач
вещ h0=1.5, v0=12, g=9.81
вещ a, b, c, D, t1, t2
a:= -g/2
b:= v0
c:= h0
D:= b*b - 4*a*c
t1:= (-b+sqrt(D))/(2*a)
t2:= (-b-sqrt(D))/(2*a)
вывод t1, нс, t2
кон
К.Ю. Поляков, Е.А. Ерёмин, 2018
Что такое a, b, c, D?
Кумир
http://kpolyakov.spb.ru

22. IV. Построение компьютерной модели

Моделирование, 9 класс
22
IV. Построение компьютерной модели
?
g tn2
Что такое a, b, c, D?
0 h0 v0 tn
2
program Polet;
Паскаль
var h0, v0, g: real;
a, b, c, D, t1, t2: real;
begin
h0:= 1.5; v0:= 12; g:= 9.81;
a:= -g/2; b:= v0; c:= h0;
D:= b*b - 4*a*c;
t1:= (-b+sqrt(D))/(2*a);
t2:= (-b-sqrt(D))/(2*a);
writeln(t1);
writeln(t2);
end.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

23. IV. Построение компьютерной модели

Моделирование, 9 класс
23
IV. Построение компьютерной модели
?
g tn2
0 h0 v0 tn
2
from math import sqrt
h0 = 1.5
v0 = 12
g = 9.81
a = -g/2
b = v0
c = h0
D = b*b - 4*a*c
t1 = (-b+sqrt(D))/(2*a)
t2 = (-b-sqrt(D))/(2*a)
print( t1 )
print( t2 )
К.Ю. Поляков, Е.А. Ерёмин, 2018
Что такое a, b, c, D?
Python
http://kpolyakov.spb.ru

24. IV. Построение компьютерной модели

Моделирование, 9 класс
24
IV. Построение компьютерной модели
?
g tn2
Что такое a, b, c, D?
0 h0 v0 tn
2
#include <iostream>
C++
#include <cmath>
using namespace std;
int main()
{
float h0, v0, g, a, b, c, D, t1, t2;
h0 = 1.5; v0 = 12; g = 9.81;
a = -g/2; b = v0; c = h0;
D = b*b - 4*a*c;
t1 = (-b+sqrt(D))/(2*a);
t2 = (-b-sqrt(D))/(2*a);
cout << t1 << endl << t2;
}
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

25. Компьютерная имитационная модель

Моделирование, 9 класс
25
Компьютерная имитационная модель
если нельзя просто решить уравнение…
интервал
дискретизации
Дискретизация задачи:
моменты времени: 0, t, 2 t, 3 t, …, ti = i t
y
0 t
t
Рассматриваем [ti, ti+1]
Знаем yi и vi при t = ti получить yi+1 и vi+1 при t = ti +1
!
Считаем, что скорость
меняется скачком!
К.Ю. Поляков, Е.А. Ерёмин, 2018
yi+1 = yi + vi t
vi+1 = vi – g t
http://kpolyakov.spb.ru

26. Компьютерная имитационная модель

Моделирование, 9 класс
26
Компьютерная имитационная модель
алг Полёт-2
Кумир
нач
вещ h0=1.5, v0=12, g=9.81
вещ y, v, t, dt=0.01
y:= h0; v:= v0; t:= 0
нц пока y >= 0
y:= y + v*dt
Что такое y, v, t, dt?
v:= v - g*dt
t:= t + dt
кц
вывод t
кон
?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

27. Компьютерная имитационная модель

Моделирование, 9 класс
27
Компьютерная имитационная модель
program Polet_2;
Паскаль
var h0, v0, g: real;
y, v, t, dt: real;
begin
h0:= 1.5; v0:= 12; g:= 9.81;
dt:= 0.01;
y:= h0; v:= v0; t:= 0;
while y>=0 do begin
y:= y + v*dt;
v:= v - g*dt;
Что такое y, v, t, dt?
t:= t + dt;
end;
writeln(t);
end.
?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

28. Компьютерная имитационная модель

Моделирование, 9 класс
28
Компьютерная имитационная модель
h0 = 1.5
v0 = 12
g = 9.81
dt = 0.01
y = h0; v = v0; t = 0
while y>=0:
y = y + v*dt
v = v - g*dt
t = t + dt
print( t )
К.Ю. Поляков, Е.А. Ерёмин, 2018
Python
?
Что такое y, v, t, dt?
http://kpolyakov.spb.ru

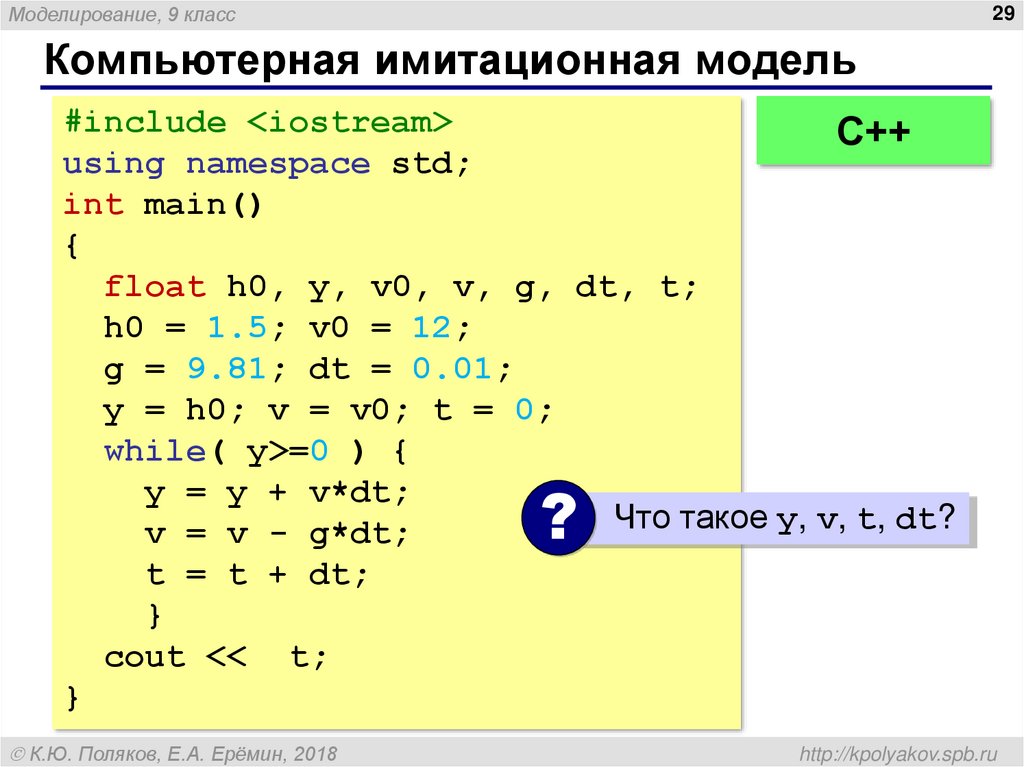
29. Компьютерная имитационная модель

Моделирование, 9 класс
29
Компьютерная имитационная модель
#include <iostream>
С++
using namespace std;
int main()
{
float h0, y, v0, v, g, dt, t;
h0 = 1.5; v0 = 12;
g = 9.81; dt = 0.01;
y = h0; v = v0; t = 0;
while( y>=0 ) {
y = y + v*dt;
Что такое y, v, t, dt?
v = v - g*dt;
t = t + dt;
}
cout << t;
}
?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

30. V. Эксперимент с моделью

Моделирование, 9 класс
30
V. Эксперимент с моделью
Эксперимент – это исследование модели при тех
исходных данных, которые нас интересуют (результат
заранее неизвестен).
!
Можно ли верить результатам?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

31. VI. Анализ результатов

Моделирование, 9 класс
31
VI. Анализ результатов
!
Необходима проверка на оригинале!
Возможные выводы:
• задача решена, модель адекватна
• необходимо изменить алгоритм или условия
моделирования
• необходимо изменить модель (учесть
дополнительные свойства)
• необходимо изменить постановку задачи
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru

English Русский Rules