Similar presentations:
Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей
1. Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей.
2. Основными фигурами в пространстве являются точка, прямая и плоскость. Изображать плоскость будем в виде параллелограмма или в виде произв
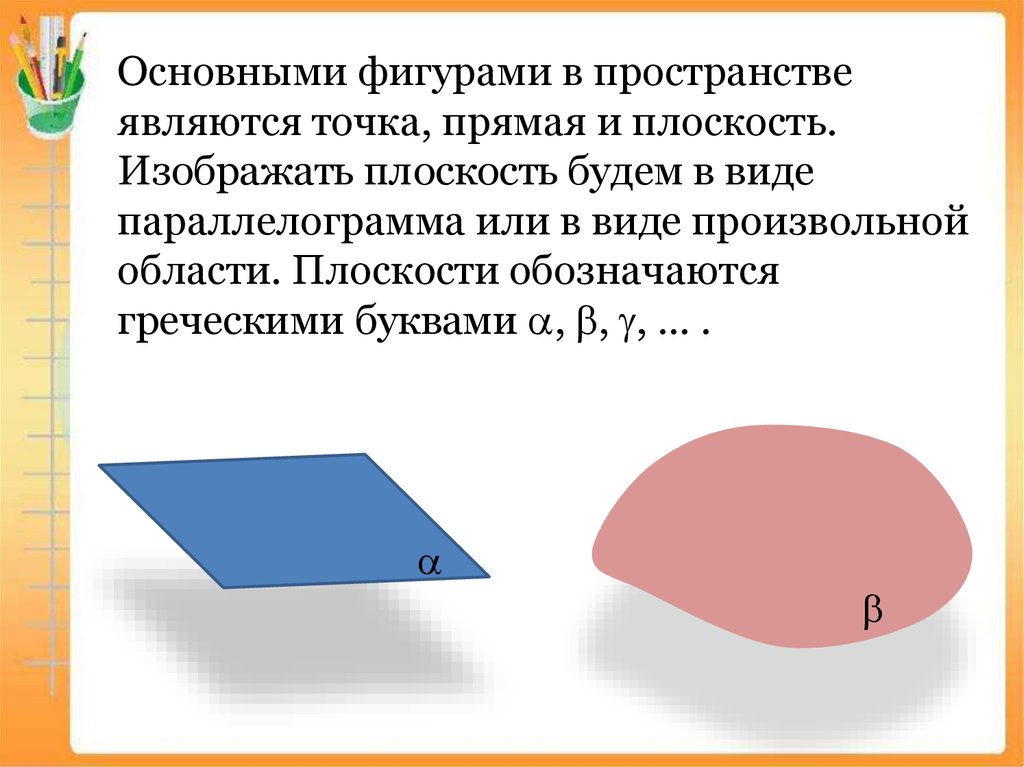
Основными фигурами в пространствеявляются точка, прямая и плоскость.
Изображать плоскость будем в виде
параллелограмма или в виде произвольной
области. Плоскости обозначаются
греческими буквами , , , … .
3. Взаимное расположение прямых в пространстве:
1.Пересекаются2.Параллельны
3.Скрещиваются
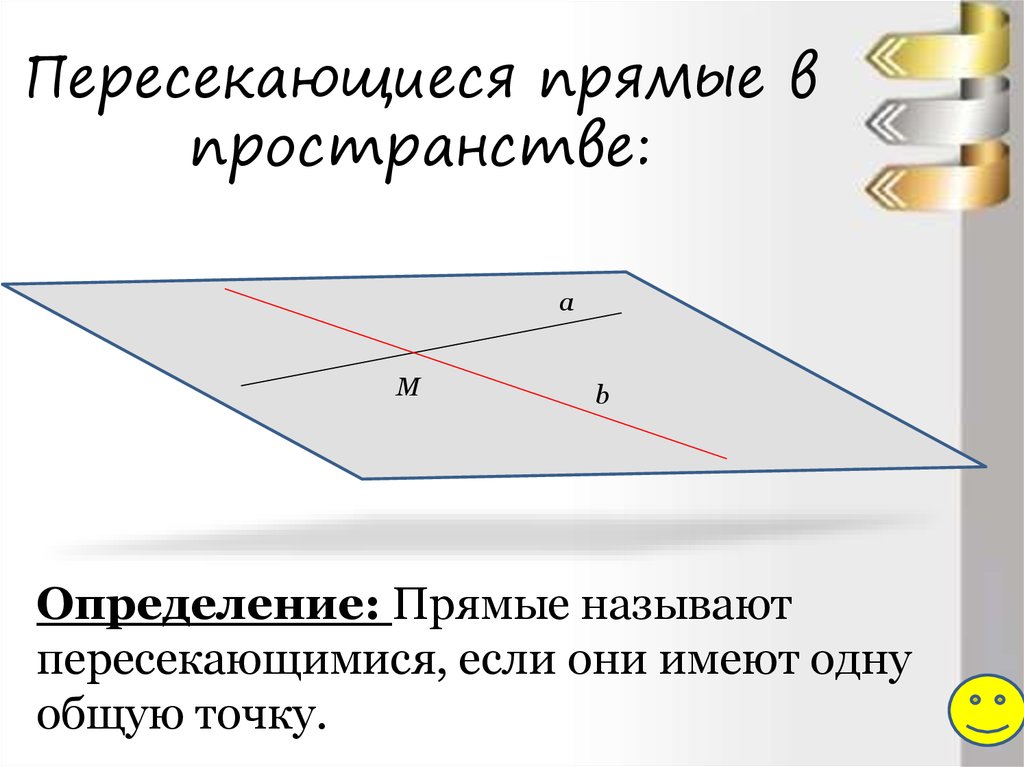
4. Пересекающиеся прямые в пространстве:
аM
b
Определение: Прямые называют
пересекающимися, если они имеют одну
общую точку.
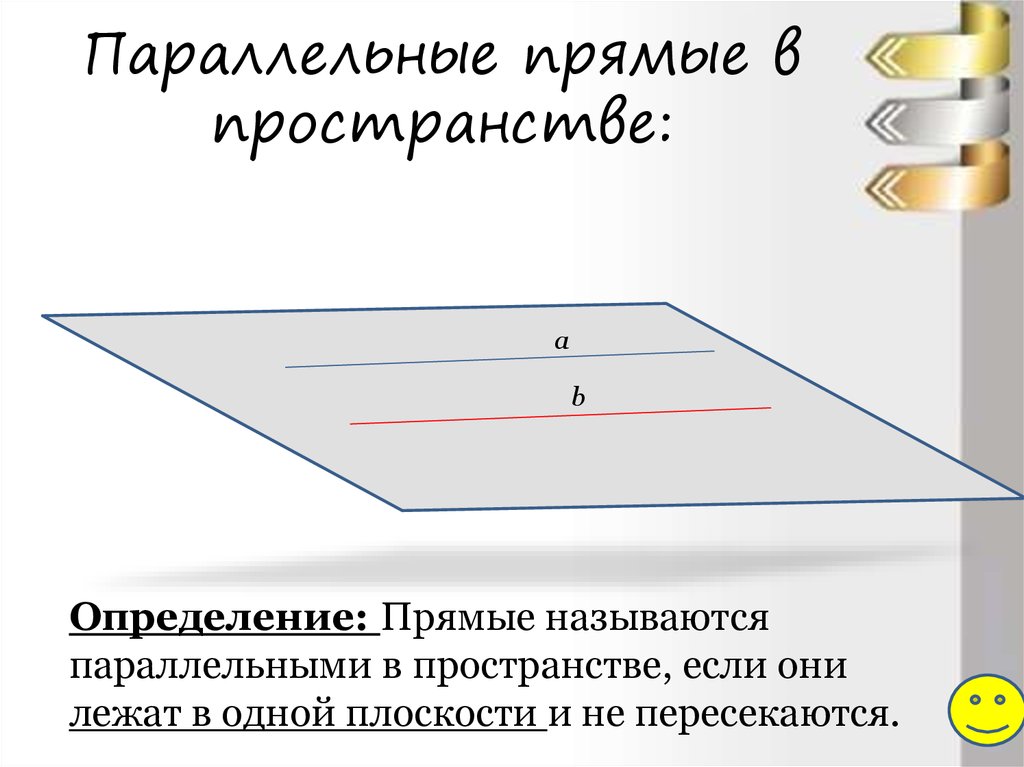
5. Параллельные прямые в пространстве:
аb
Определение: Прямые называются
параллельными в пространстве, если они
лежат в одной плоскости и не пересекаются.
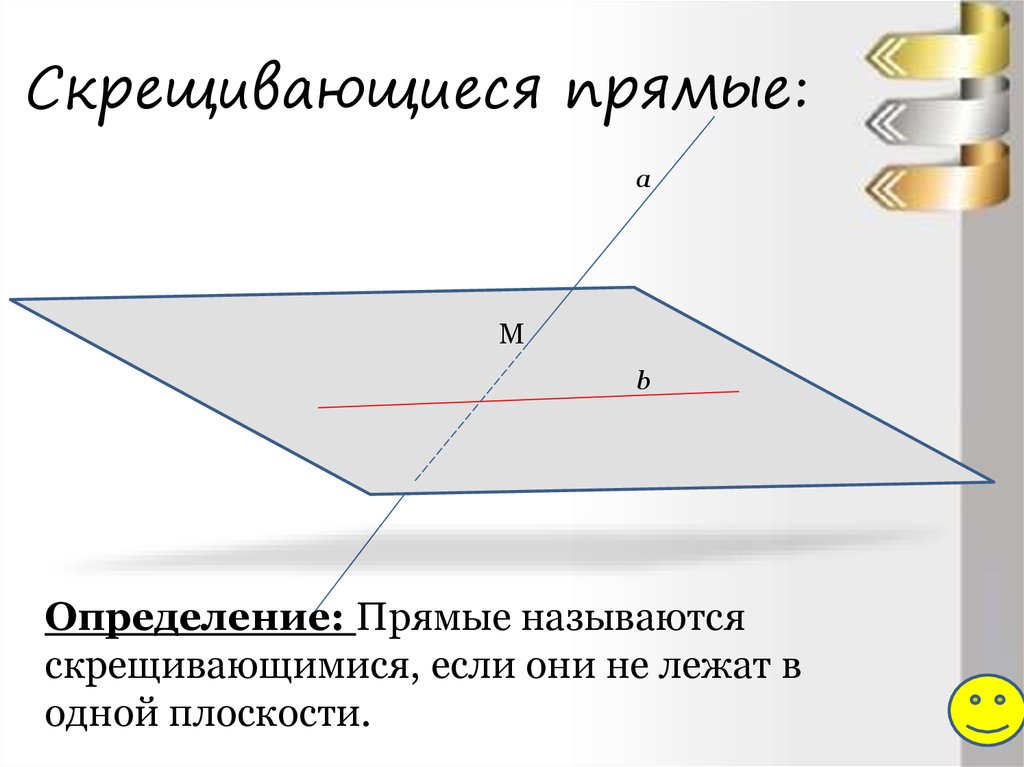
6. Скрещивающиеся прямые:
аМ
b
Определение: Прямые называются
скрещивающимися, если они не лежат в
одной плоскости.
7. Взаимное расположение прямой и плоскости в пространстве:
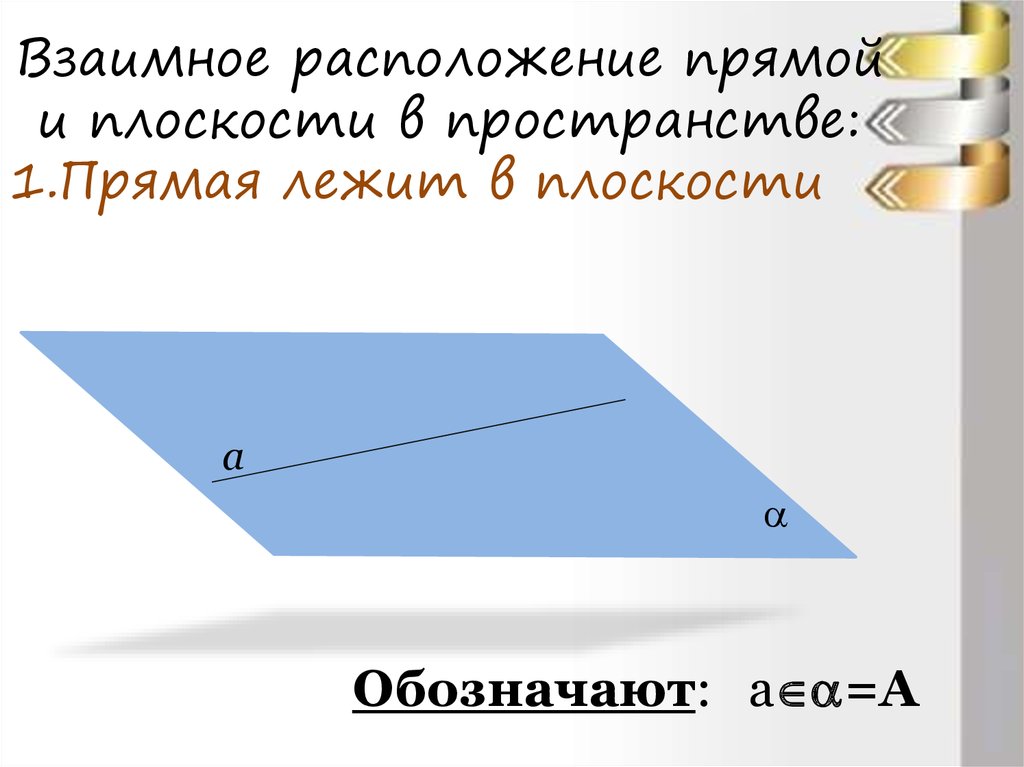
1.Прямая лежит в плоскостиа
Обозначают: а =A
8. Взаимное расположение прямой и плоскости в пространстве:
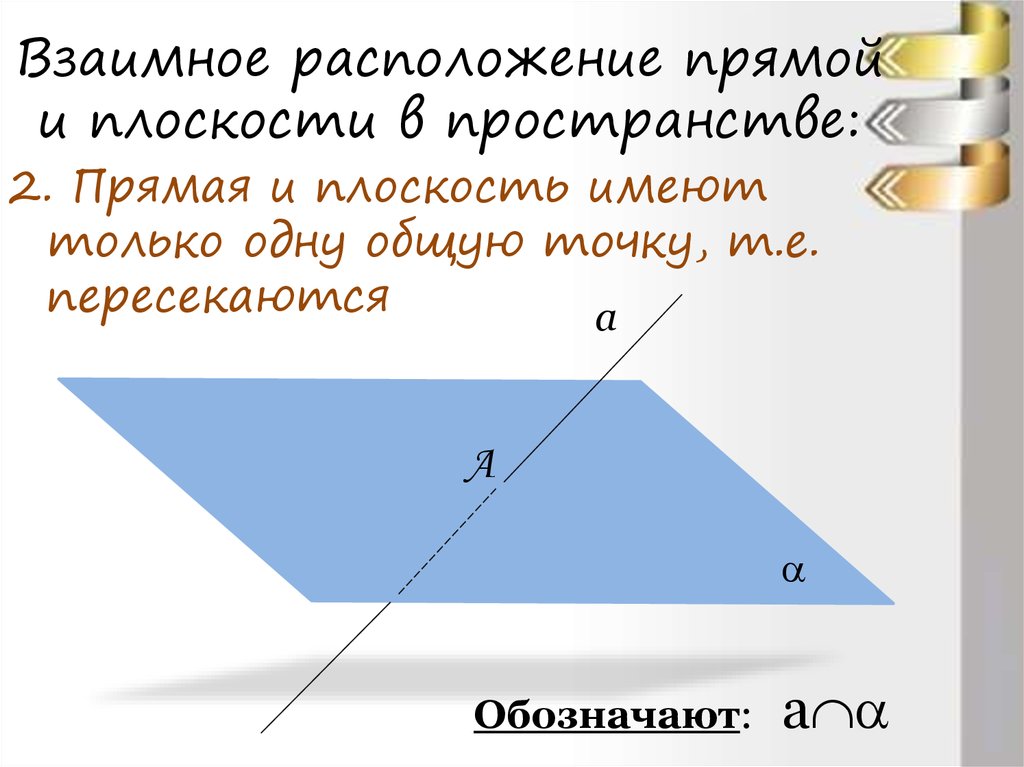
2. Прямая и плоскость имеюттолько одну общую точку, т.е.
пересекаются
а
А
Обозначают:
а
9. Взаимное расположение прямой и плоскости в пространстве:
3. Прямая и плоскость неимеют ни одной общей точки
а
Определение: Прямая и плоскость называются
параллельными, если они не имеют общих точек.
(обозначают: а ).
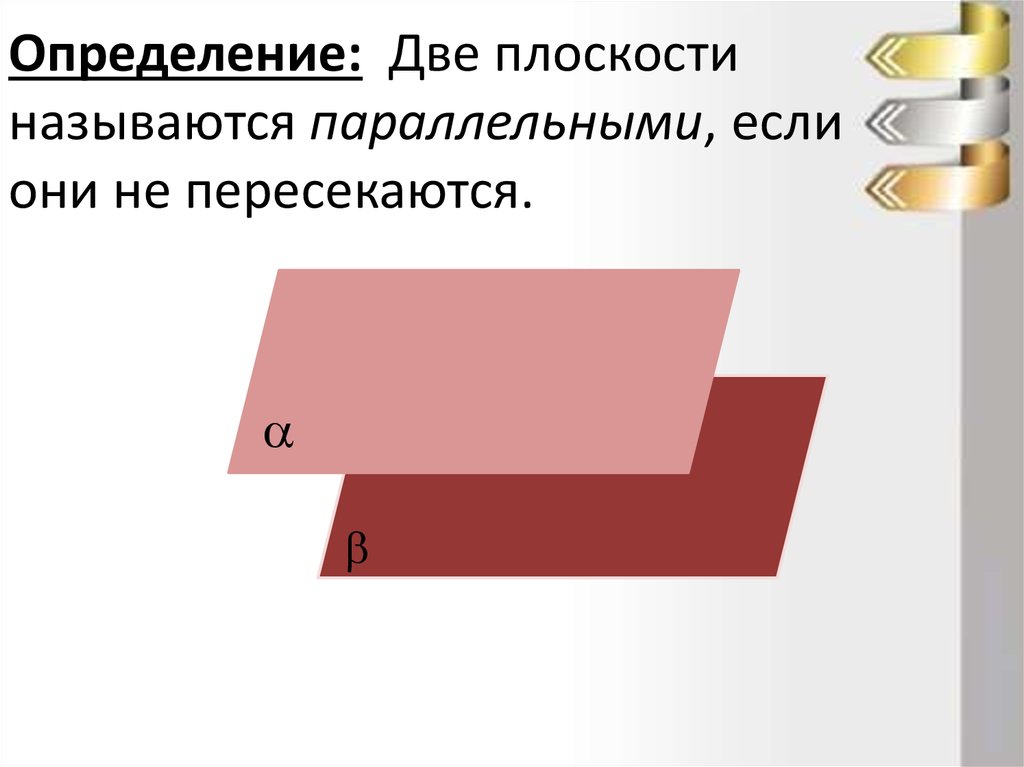
10. Определение: Две плоскости называются параллельными, если они не пересекаются.
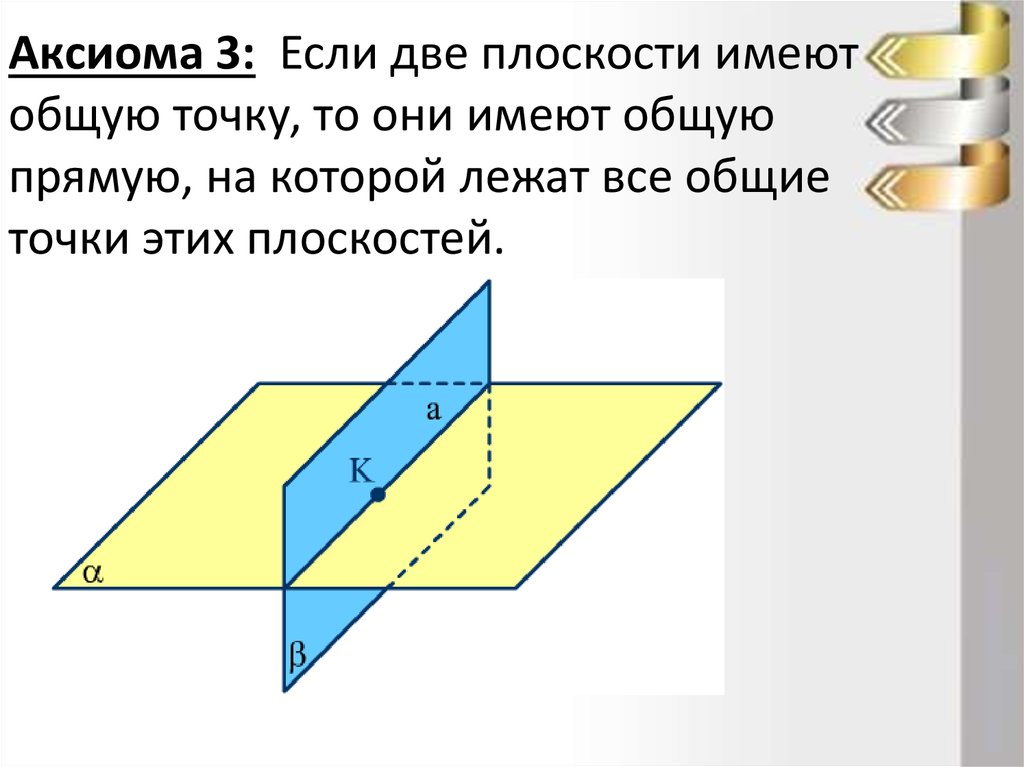
11. Аксиома 3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
12. Задача №1 На рисунке точки M, N, Q и Р – середины отрезков DB, DC, AC и AB. Найдите периметр четырехугольника MNQP, если AD=12см, BC=14 см.
13. Задача №2 Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С – параллельные прямые, пересекающие эту плоско
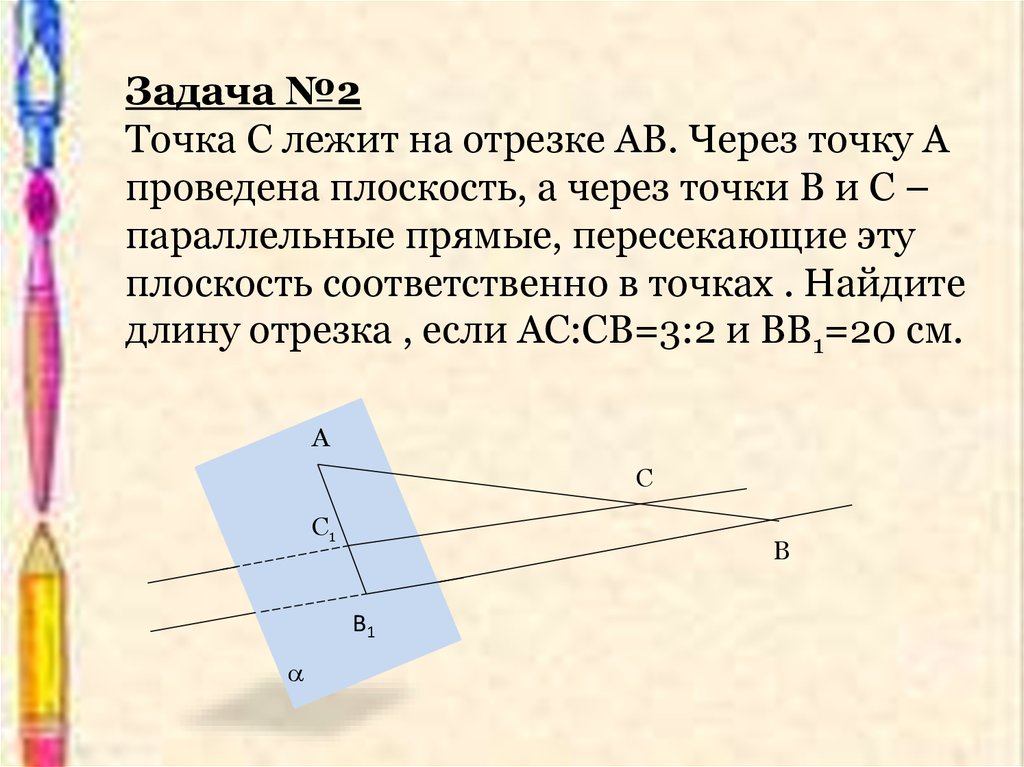
Задача №2Точка С лежит на отрезке АВ. Через точку А
проведена плоскость, а через точки В и С –
параллельные прямые, пересекающие эту
плоскость соответственно в точках . Найдите
длину отрезка , если АС:СВ=3:2 и ВВ1=20 см.
A
C
C1
B
B1
14. Задача №3 Точка D не лежит в плоскости треугольника АВС, точки M, N и Р – середины отрезков DA, DB и DC соответственно, точка К лежит на отрезке BN.
Задача №3Точка D не лежит в плоскости треугольника
АВС, точки M, N и Р – середины отрезков
DA, DB и DC соответственно, точка К лежит
на отрезке BN. Выясните взаимное
расположение прямых:
а) ND и AB;
б) MN и AB;
в) KN и AC;
г) MD и BC.
15. Задача №4 Точка В не лежит в плоскости треугольника ADC, точки M,N и Р- середины отрезков BA, BC и BD соответственно. а) Докажите, что плоскости MNP и A
Задача №4Точка В не лежит в плоскости треугольника
ADC, точки M,N и Р- середины отрезков BA,
BC и BD соответственно.
а) Докажите, что плоскости MNP и ADC
параллельны.
б) Найдите площадь треугольника
MNP, если площадь
треугольника ADC равна 48 см2.
16. Домашнее задание:
№№ 5 и 6Выучить записи в
тетради
(подготовиться к
проверочной работе)







 mathematics
mathematics








