Similar presentations:
Взаимное расположение прямых в пространстве
1. Взаимное расположение прямых в пространстве
Скрещивающиесяпрямые
2. Взаимное расположение прямых в пространстве
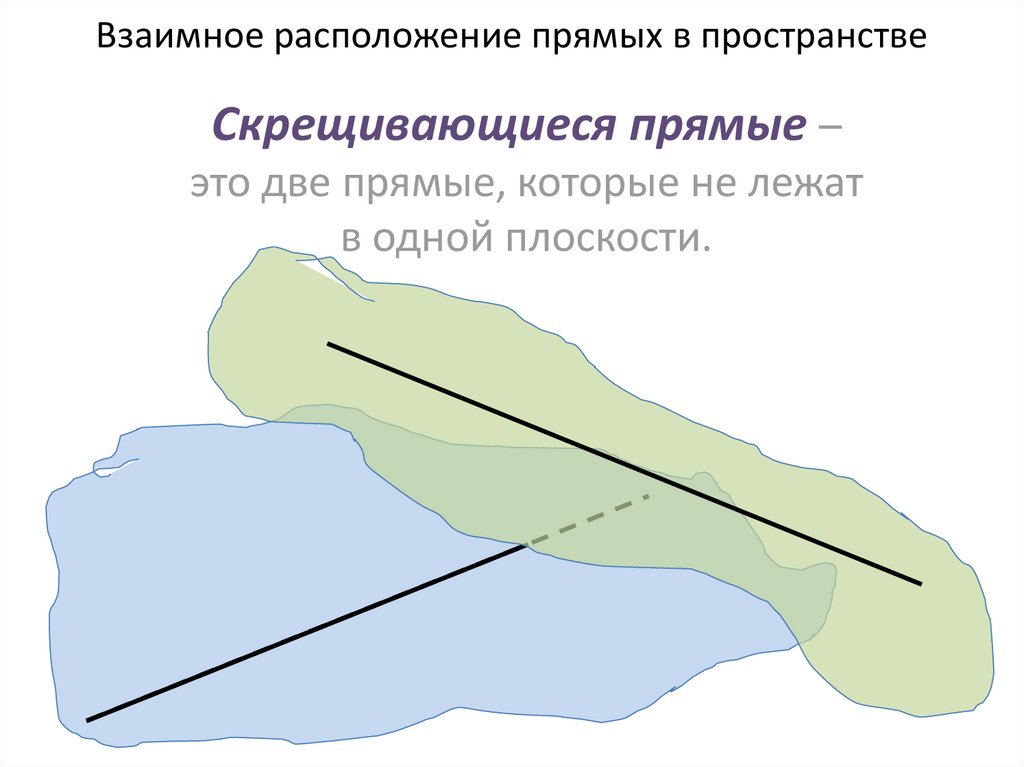
Скрещивающиеся прямые –это две прямые, которые не лежат
в одной плоскости.
3. Взаимное расположение прямых в пространстве
Скрещивающиеся прямые –это две прямые, которые не лежат
в одной плоскости.
4. Взаимное расположение прямых в пространстве
Скрещивающиеся прямые – этодве прямые, которые не лежат в
одной плоскости.
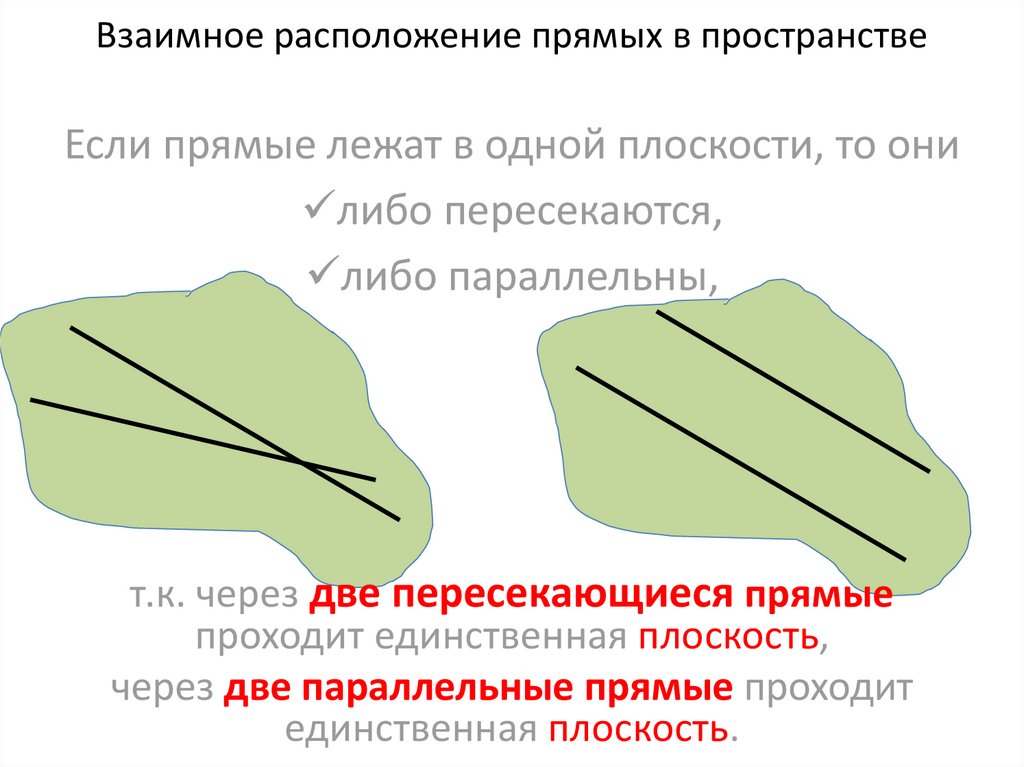
Если прямые лежат в одной плоскости, то они
либо пересекаются,
либо параллельны.
5.
Взаимное расположение прямых в пространствеЕсли прямые лежат в одной плоскости, то они
либо пересекаются,
либо параллельны,
т.к. через две пересекающиеся прямые
проходит единственная плоскость,
через две параллельные прямые проходит
единственная плоскость.
6. Взаимное расположение прямых в пространстве
Т.о выделяется три случая взаимногорасположения прямых в пространстве:
прямые параллельны,
прямые пересекаются,
прямые скрещиваются.
7. Взаимное расположение прямых в пространстве
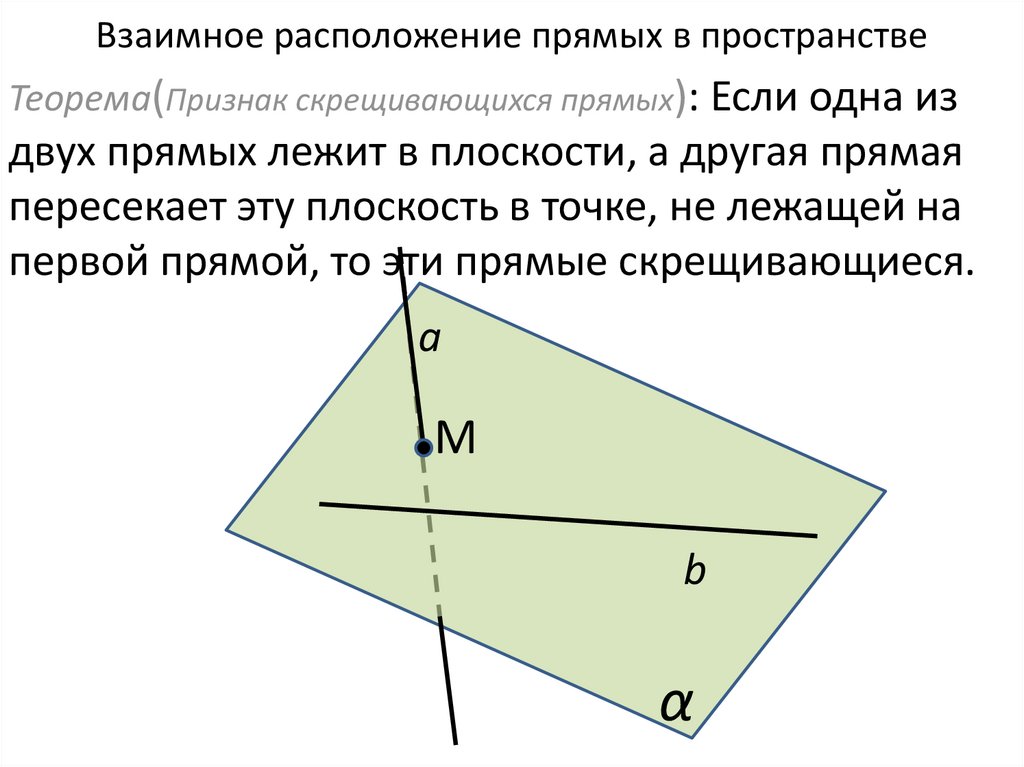
Теорема(Признак скрещивающихся прямых): Если одна издвух прямых лежит в плоскости, а другая прямая
пересекает эту плоскость в точке, не лежащей на
первой прямой, то эти прямые скрещивающиеся.
a
M
b
α
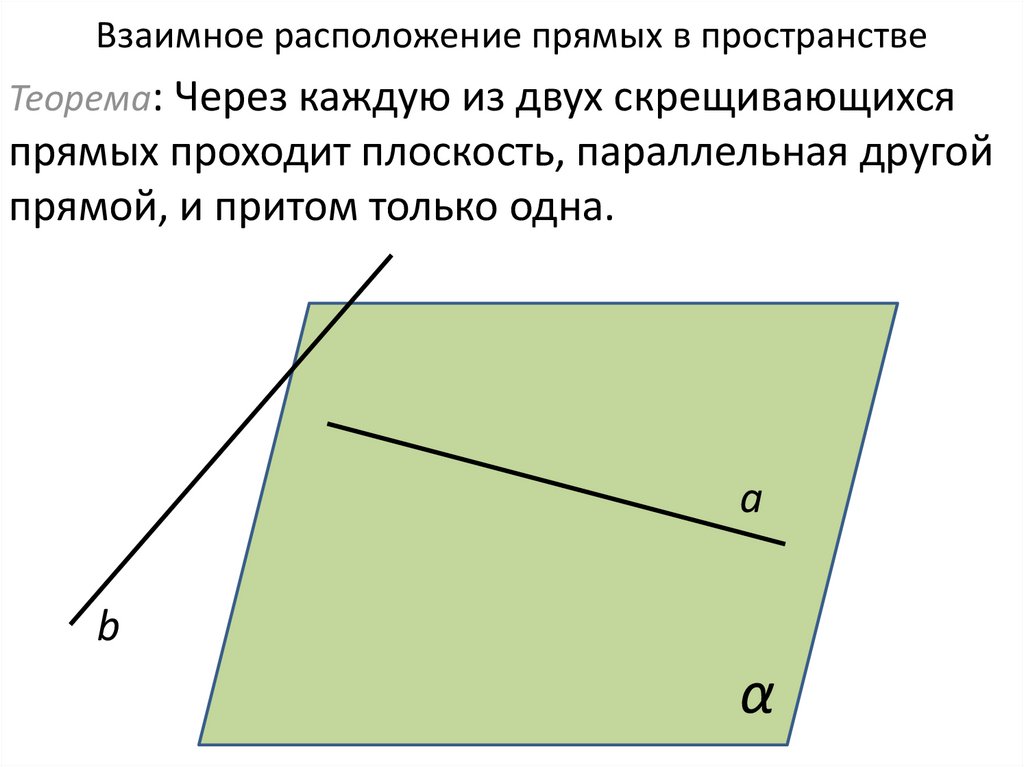
8. Взаимное расположение прямых в пространстве
Теорема: Через каждую из двух скрещивающихсяпрямых проходит плоскость, параллельная другой
прямой, и притом только одна.
a
b
α
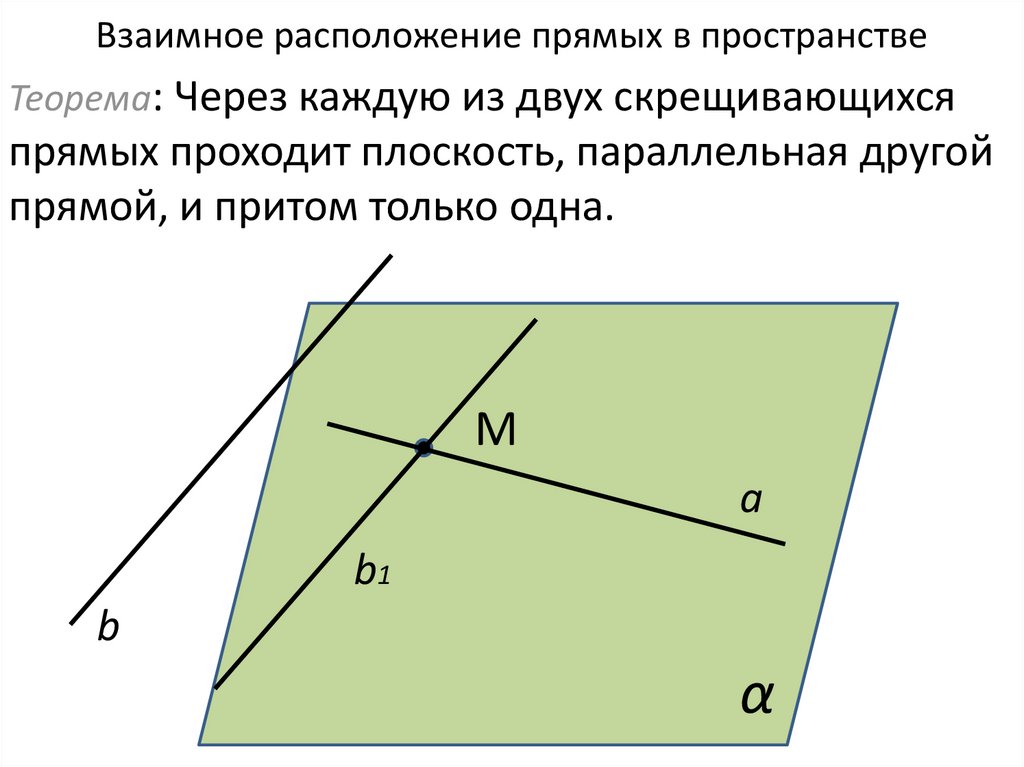
9. Взаимное расположение прямых в пространстве
Теорема: Через каждую из двух скрещивающихсяпрямых проходит плоскость, параллельная другой
прямой, и притом только одна.
M
a
b1
b
α
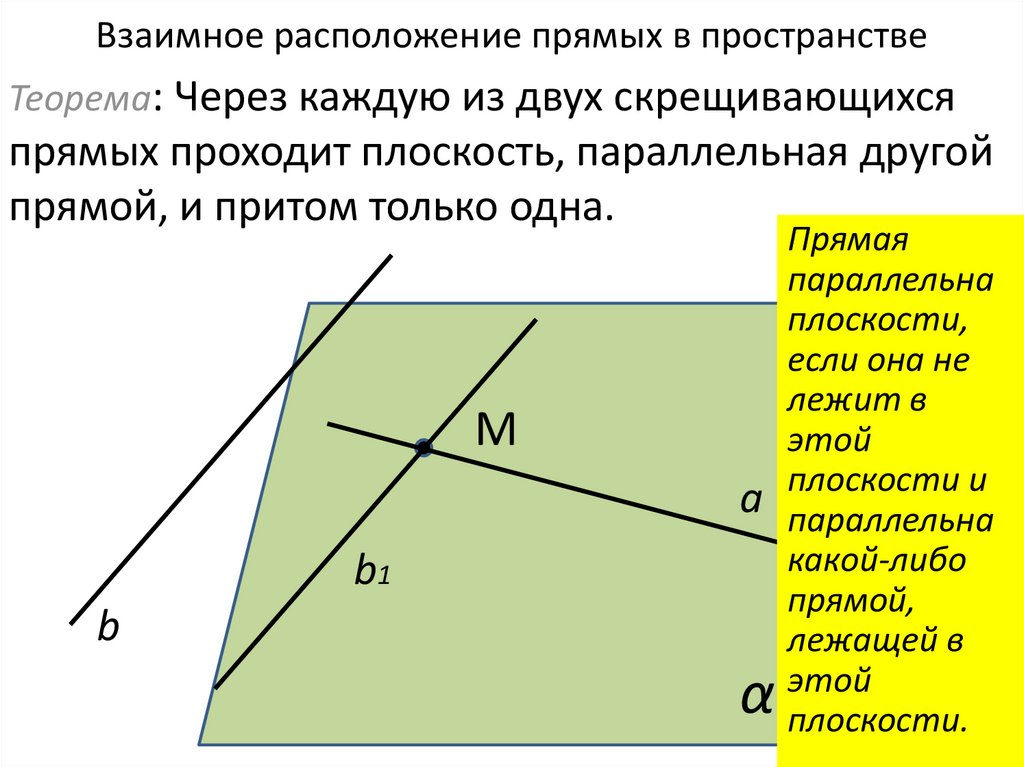
10. Взаимное расположение прямых в пространстве
Теорема: Через каждую из двух скрещивающихсяпрямых проходит плоскость, параллельная другой
прямой, и притом только одна.
M
a
b1
b
α
Прямая
параллельна
плоскости,
если она не
лежит в
этой
плоскости и
параллельна
какой-либо
прямой,
лежащей в
этой
плоскости.
11.
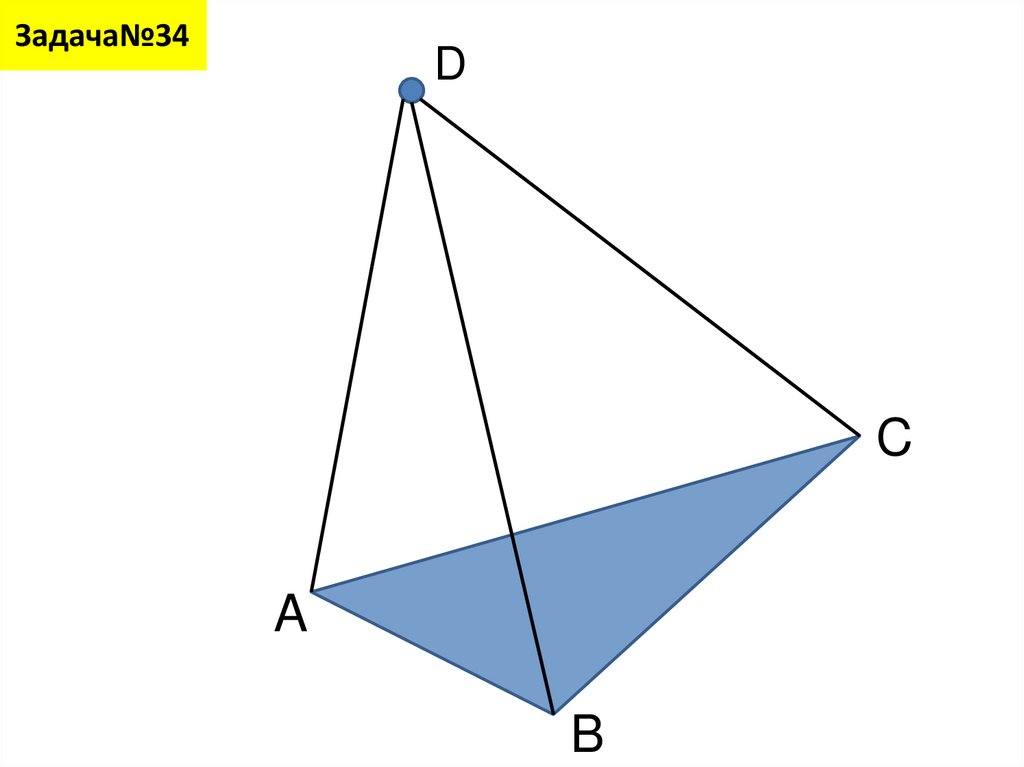
Классная работа:Решаем задачу
№ 34
СДЕЛАТЬ РИСУНОК,
РЕШЕНИЕ УСТНОЕ
12. Задача№34
DC
A
B
13. Задача№34
DP
M
N
C
A
B
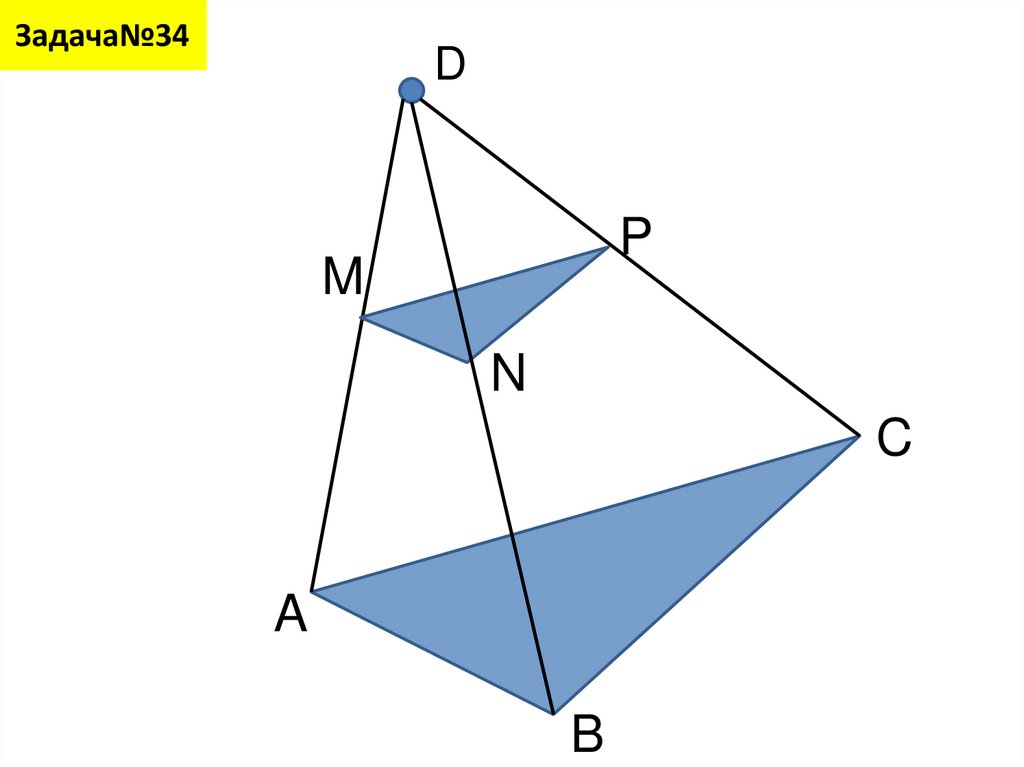
14. Задача№34
DP
M
N
C
A
B
15. Задача№34
DP
M
N
C
K
A
B
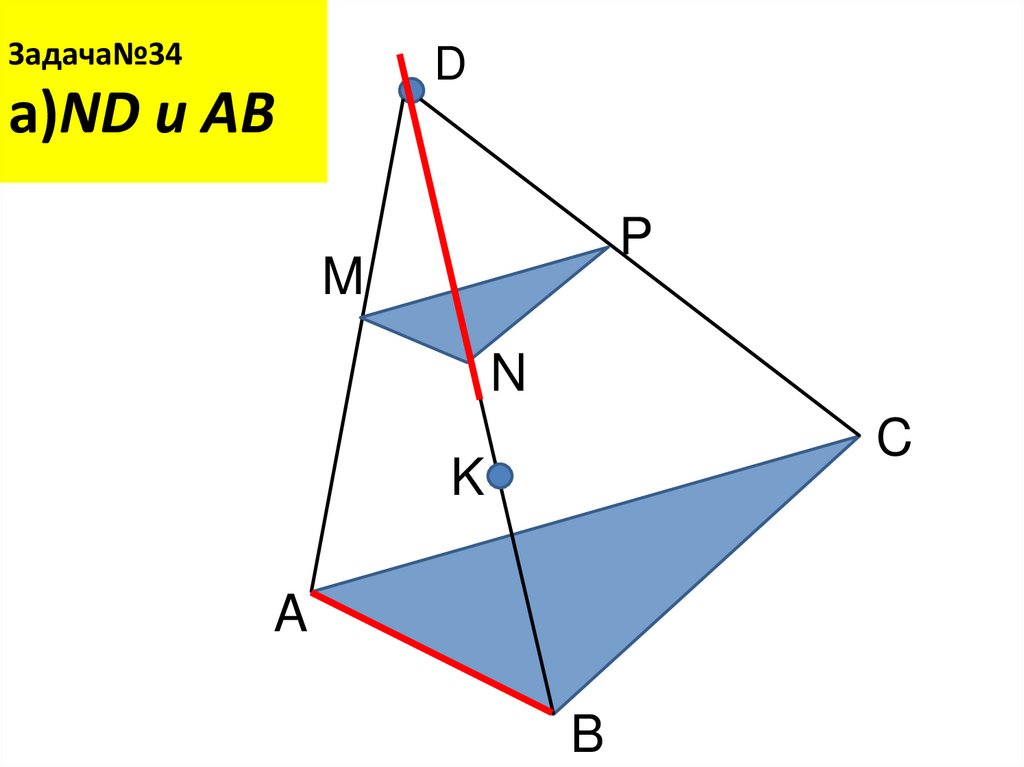
16. Задача№34 a)ND и AB
Задача№34D
a)ND и AB
P
M
N
C
K
A
B
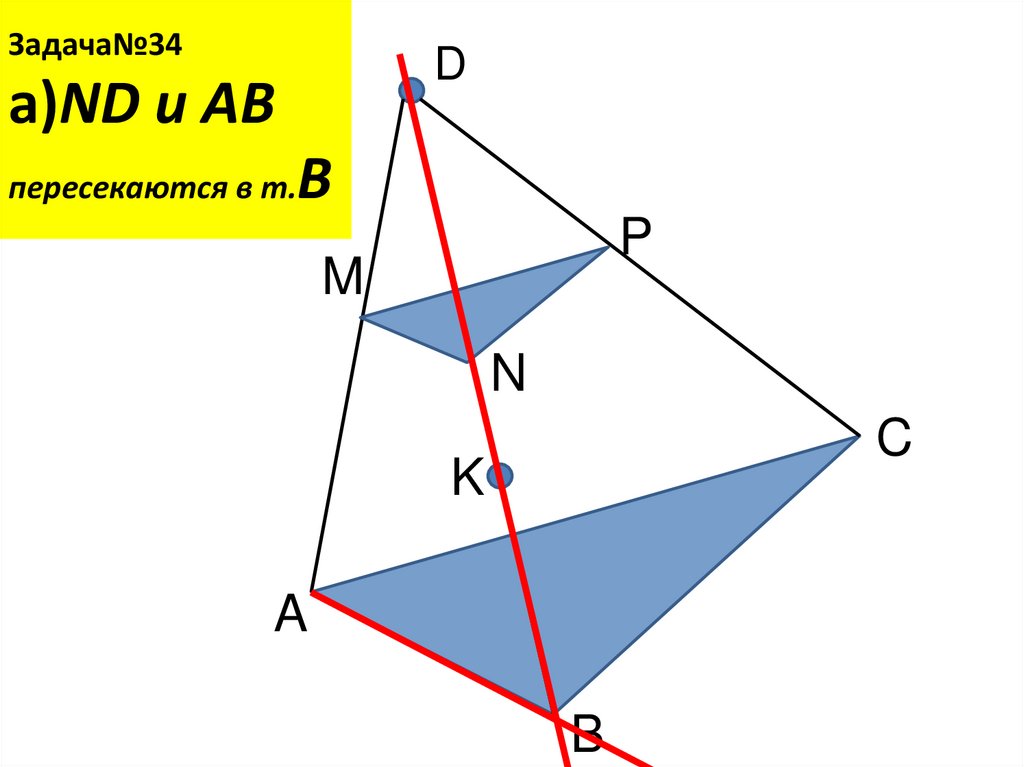
17. Задача№34 a)ND и AB пересекаются в т.В
Задача№34D
a)ND и AB
В
пересекаются в т.
P
M
N
C
K
A
B
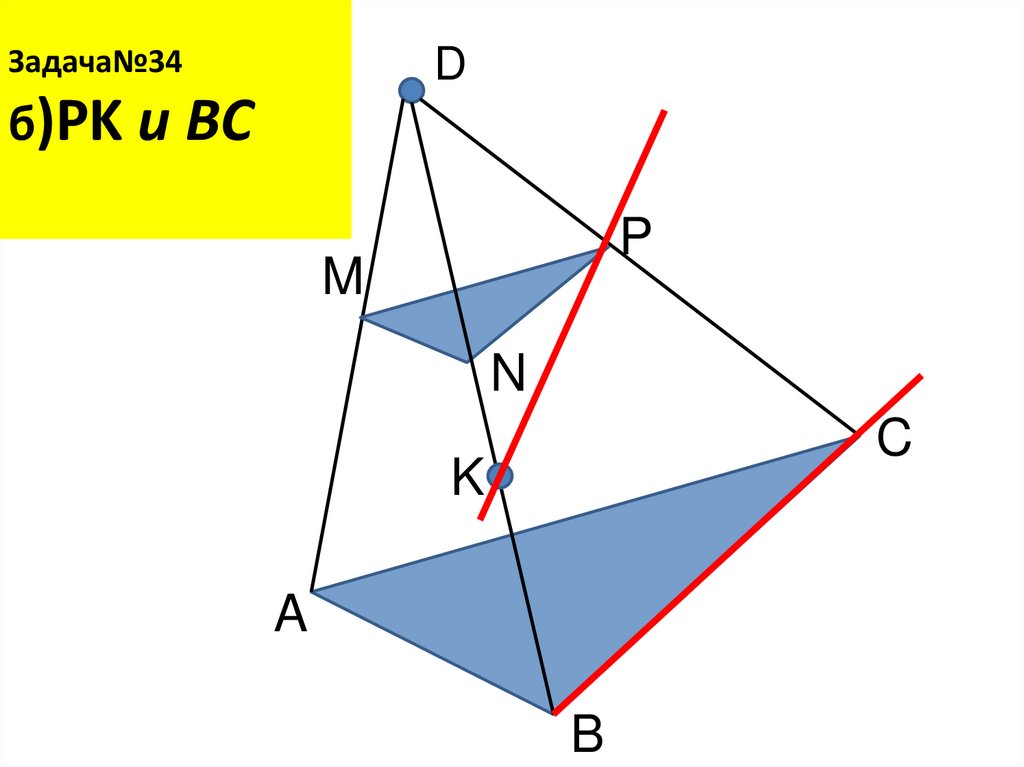
18. Задача№34 б)PK и BC
Задача№34D
б)PK и BC
P
M
N
C
K
A
B
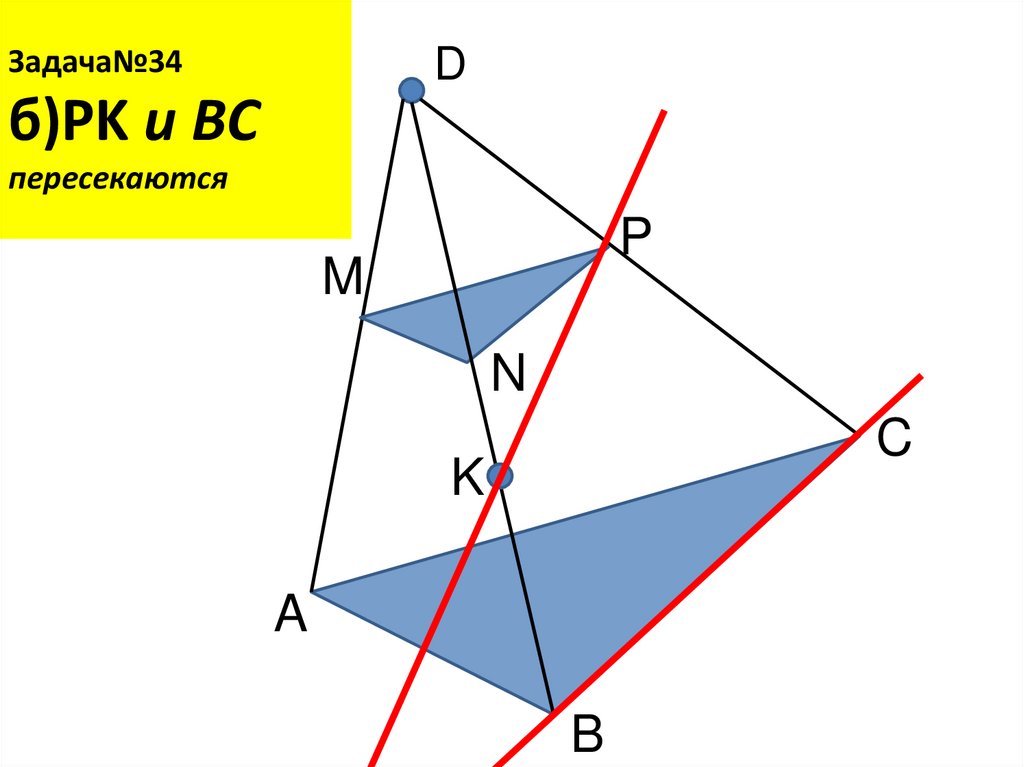
19. Задача№34 б)PK и BC пересекаются
Задача№34D
б)PK и BC
пересекаются
P
M
N
C
K
A
B
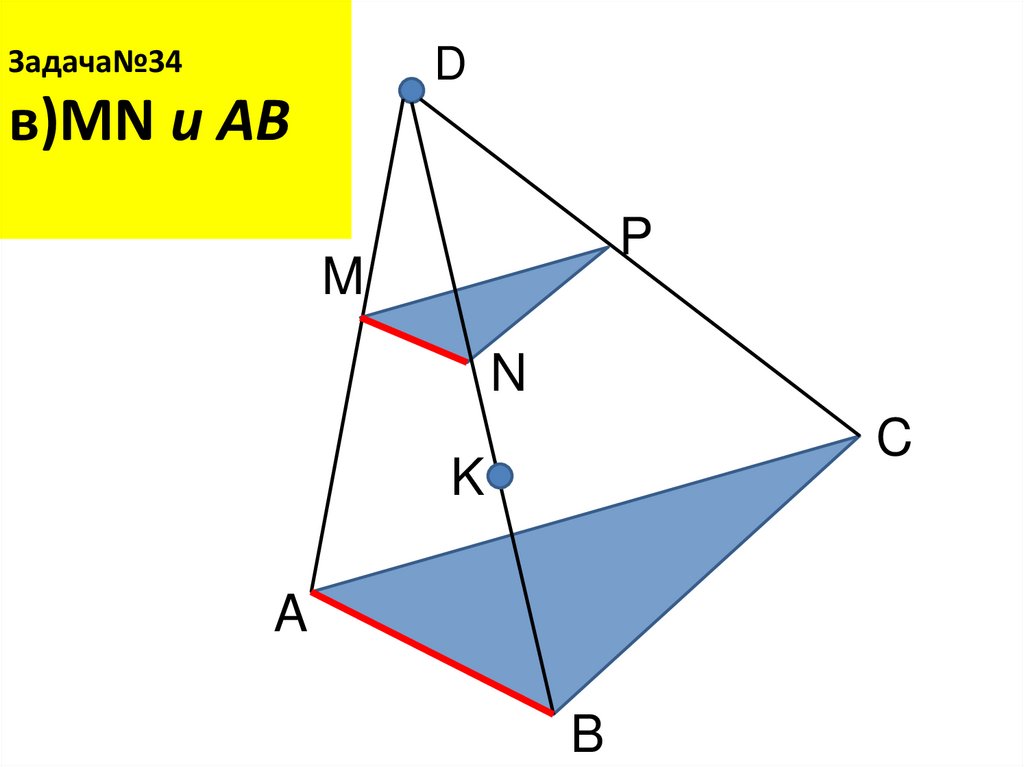
20. Задача№34 в)MN и AB
Задача№34D
в)MN и AB
P
M
N
C
K
A
B
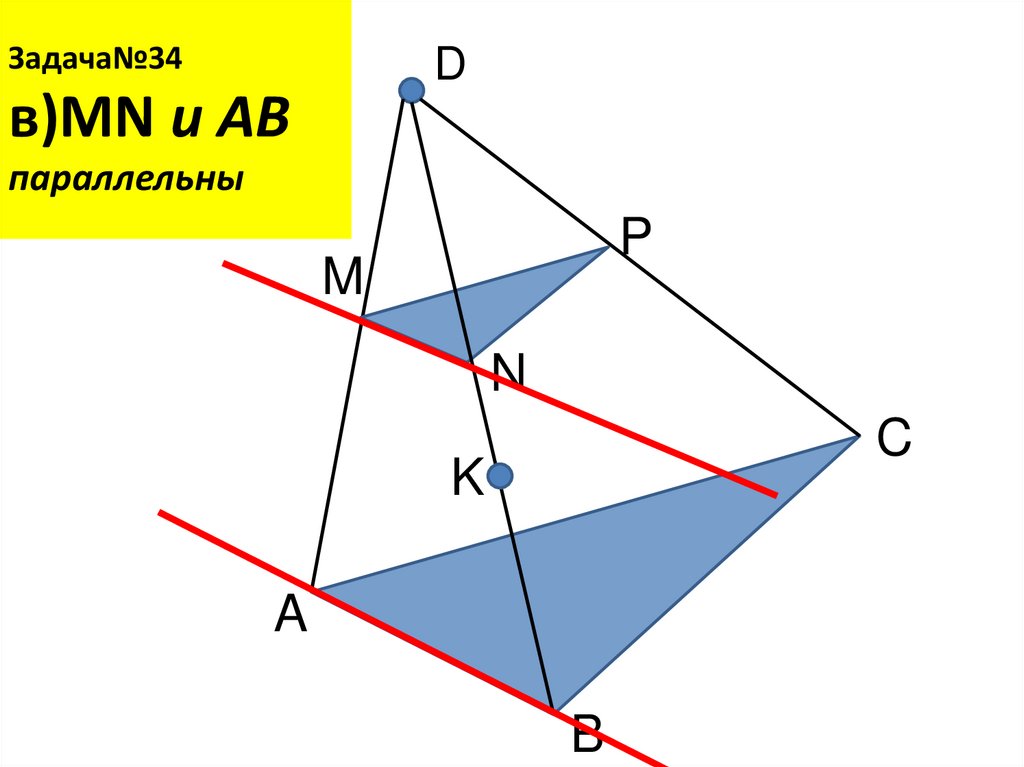
21. Задача№34 в)MN и AB параллельны
Задача№34D
в)MN и AB
параллельны
P
M
N
C
K
A
B
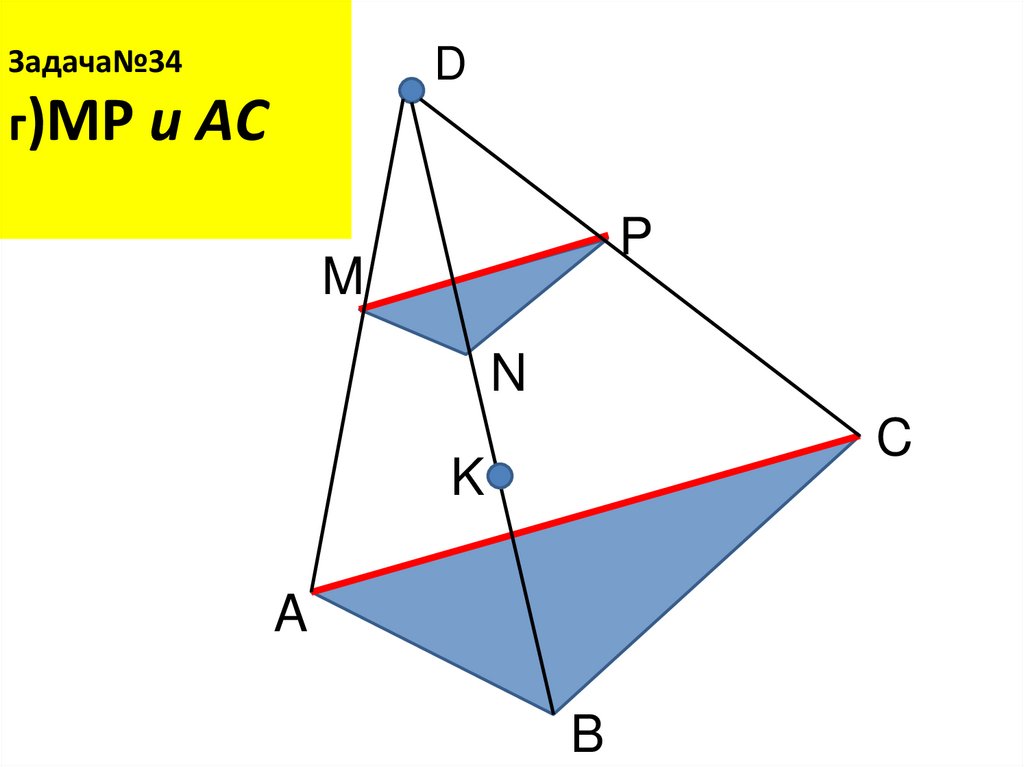
22. Задача№34 г)MР и AС
Задача№34D
г)MР и AС
P
M
N
C
K
A
B
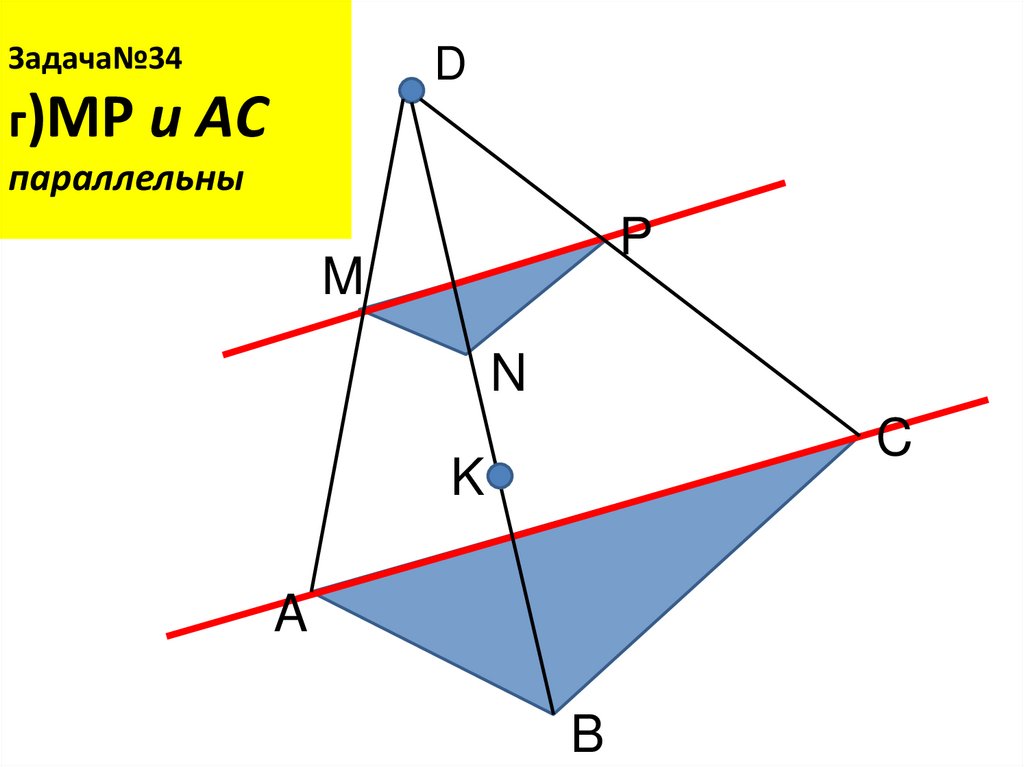
23. Задача№34 г)MР и AС параллельны
Задача№34D
г)MР и AС
параллельны
P
M
N
C
K
A
B
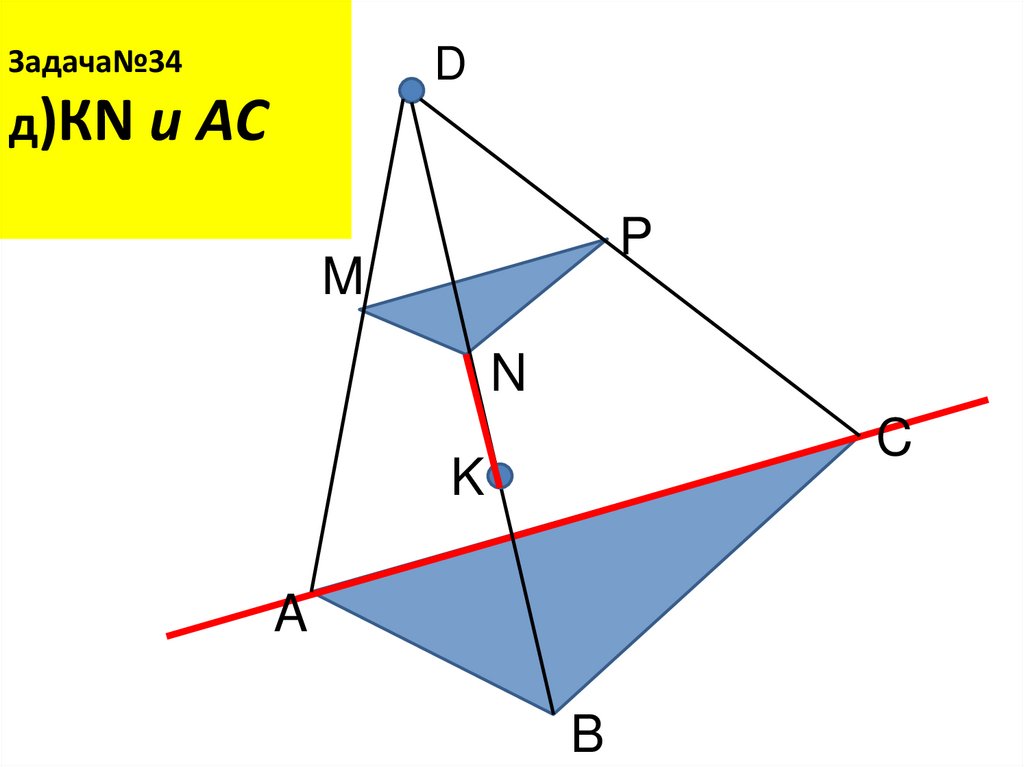
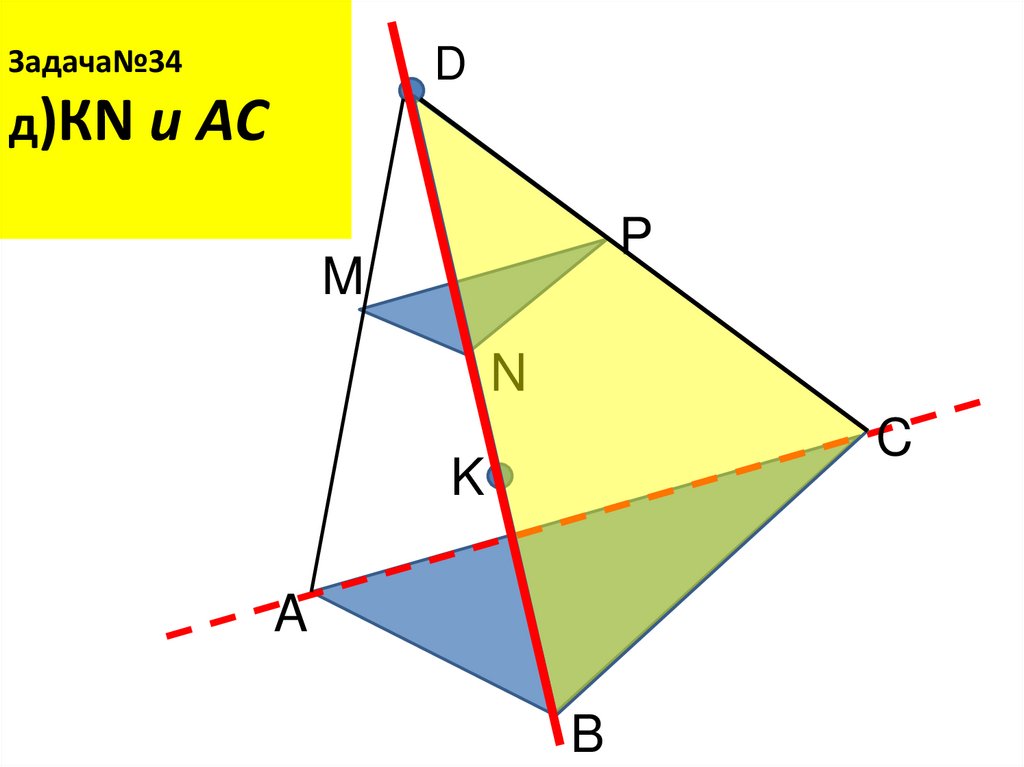
24. Задача№34 д)КN и AС
Задача№34D
д)КN и AС
P
M
N
C
K
A
B
25. Задача№34 д)КN и AС
Задача№34D
д)КN и AС
P
M
N
C
K
A
B
26. Задача№34 д)КN и AС
Задача№34D
д)КN и AС
P
M
N
C
K
A
B
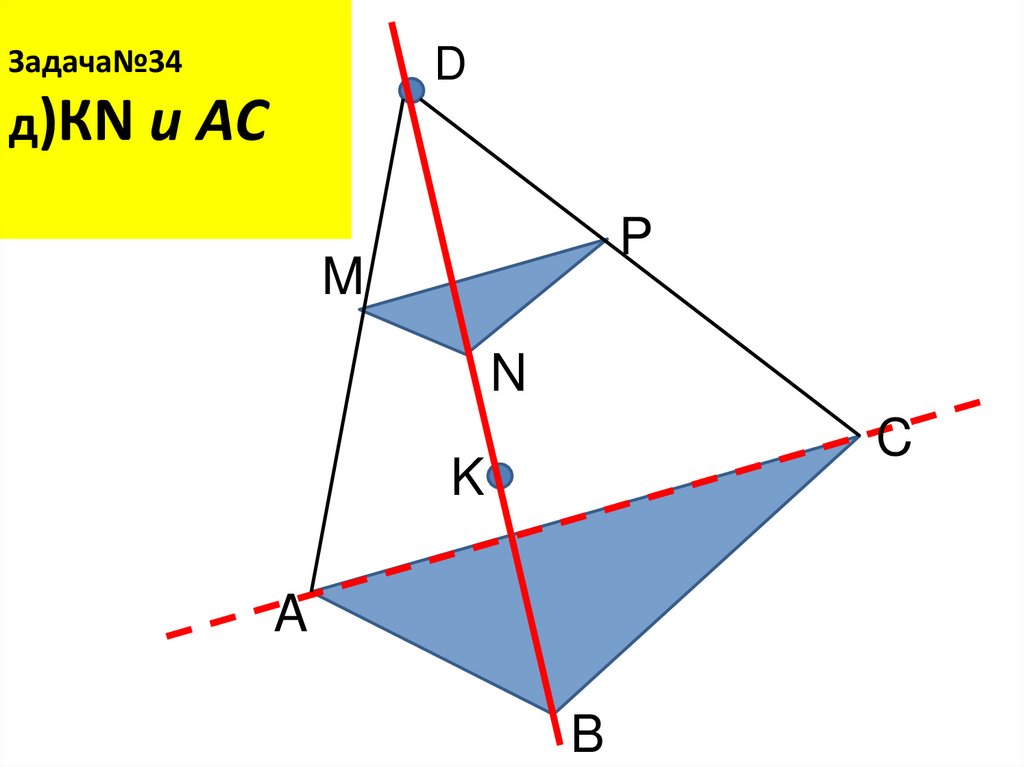
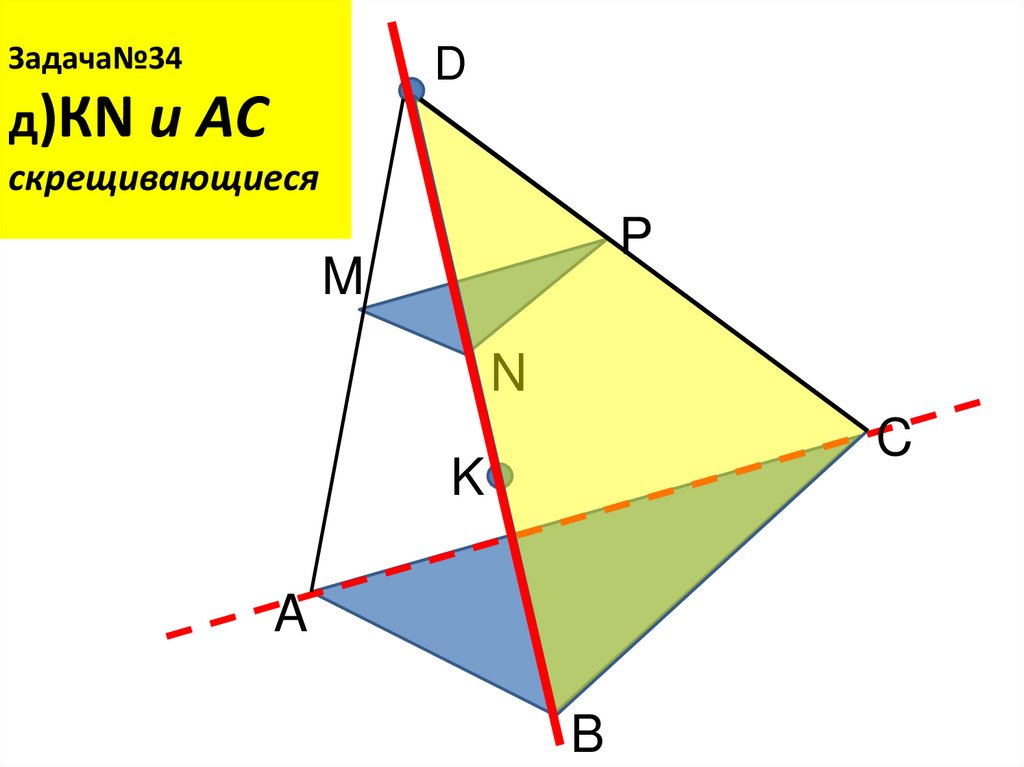
27. Задача№34 д)КN и AС скрещивающиеся
Задача№34D
д)КN и AС
скрещивающиеся
P
M
N
C
K
A
B
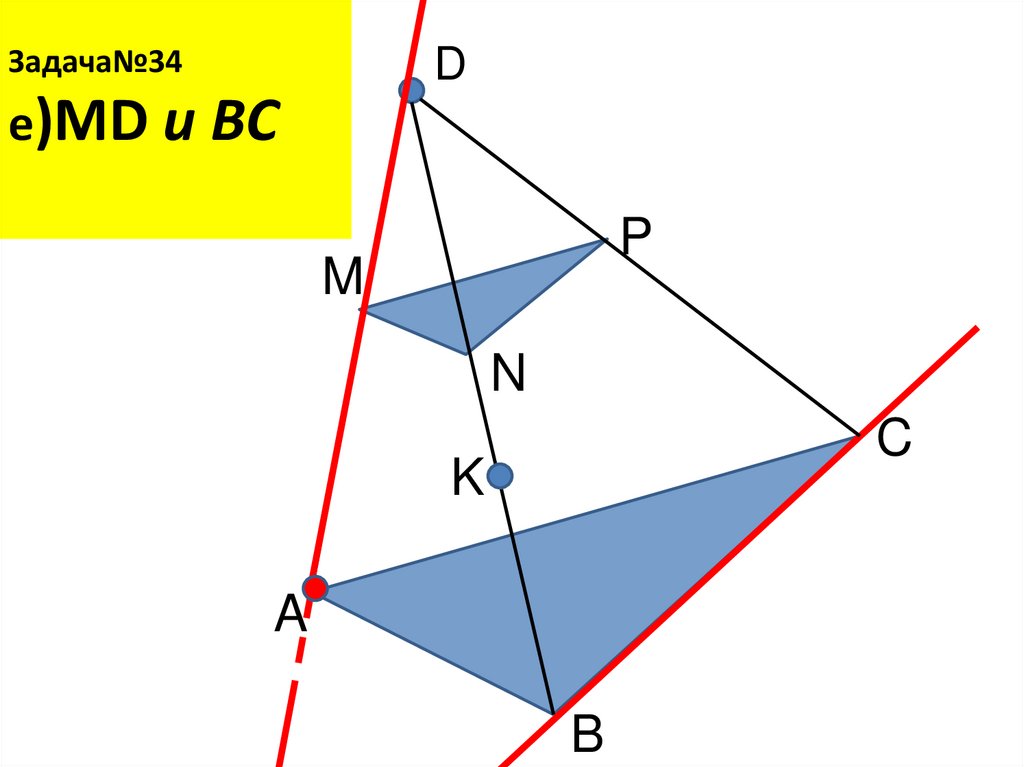
28. Задача№34 е)MD и BС
Задача№34D
е)MD и BС
P
M
N
C
K
A
B
29. Задача№34 е)MD и BС
Задача№34D
е)MD и BС
P
M
N
C
K
A
B
30. Задача№34 е)MD и BС
Задача№34D
е)MD и BС
P
M
N
C
K
A
B
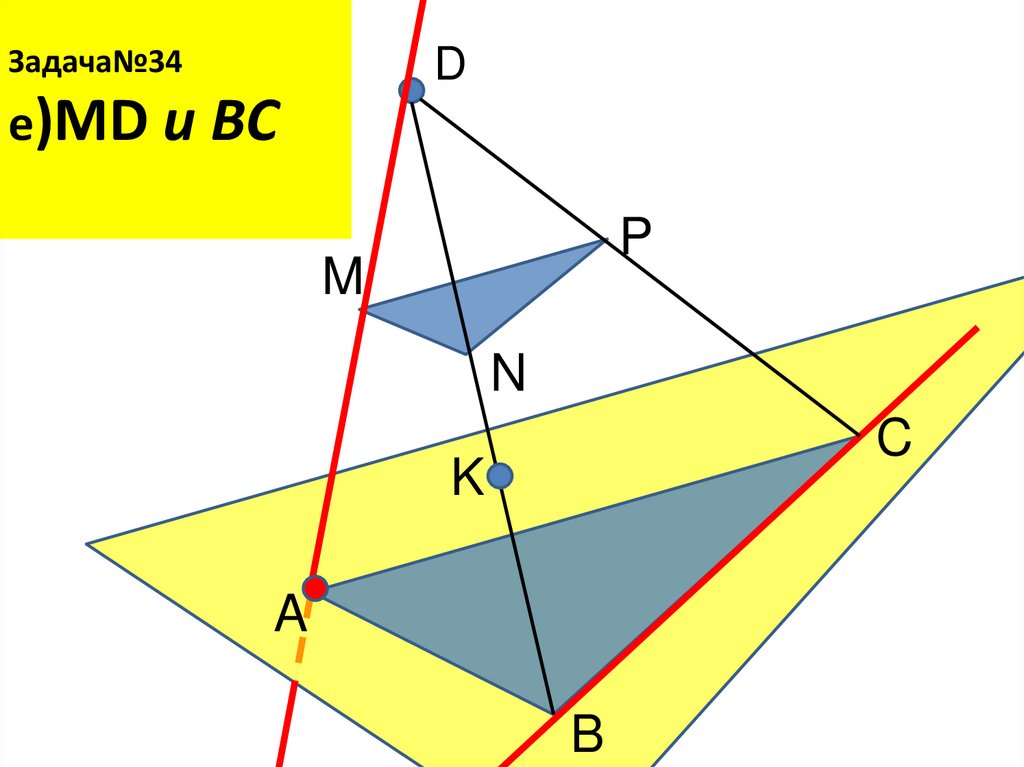
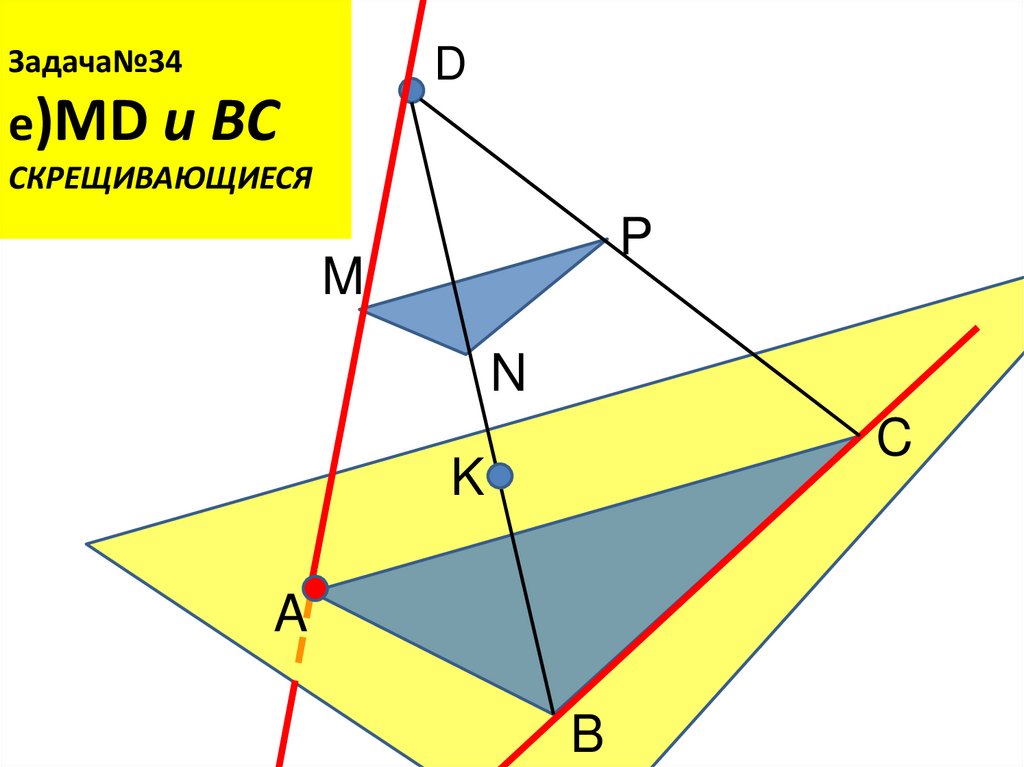
31. Задача№34 е)MD и BС СКРЕЩИВАЮЩИЕСЯ
Задача№34D
е)MD и BС
СКРЕЩИВАЮЩИЕСЯ
P
M
N
C
K
A
B
32. Взаимное расположение прямых в пространстве
Два луча МА и NB называются сонаправленными,если они
параллельны и
M
N
A
B
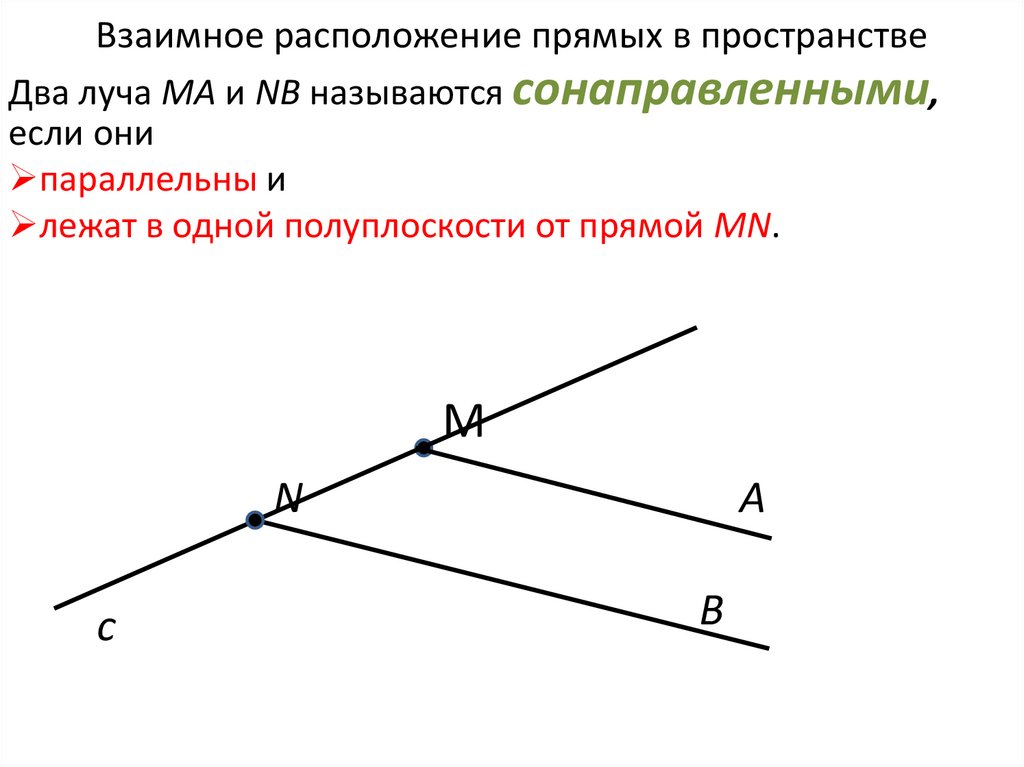
33. Взаимное расположение прямых в пространстве
Два луча МА и NB называются сонаправленными,если они
параллельны и
лежат в одной полуплоскости от прямой MN.
M
N
c
A
B
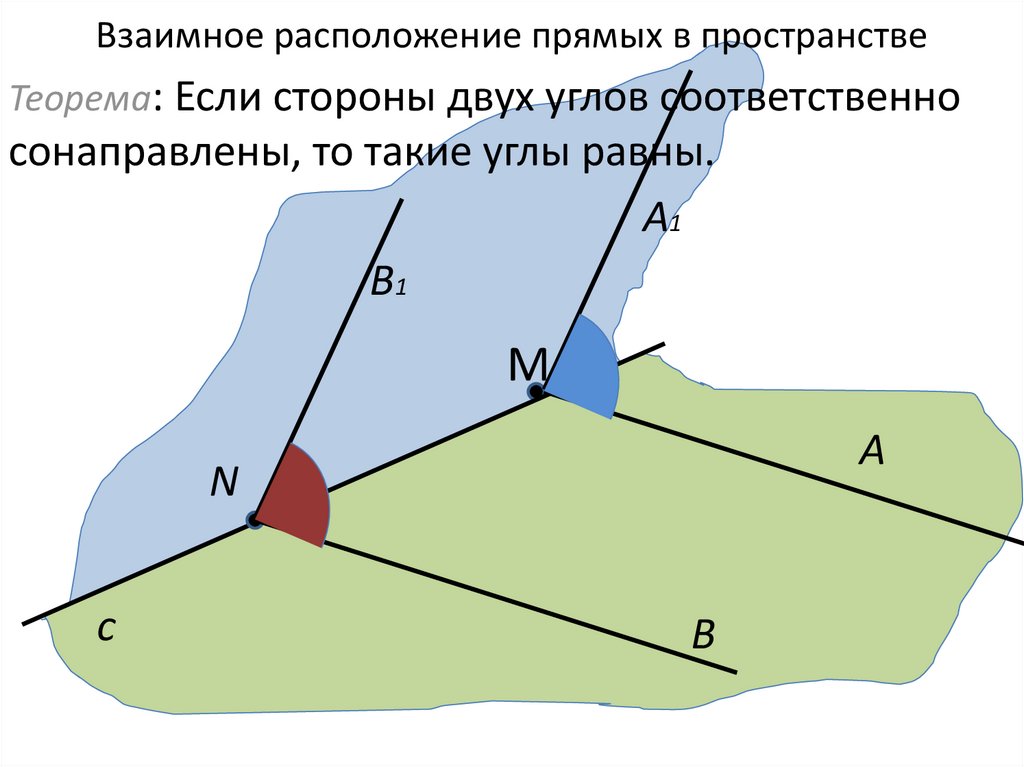
34. Взаимное расположение прямых в пространстве
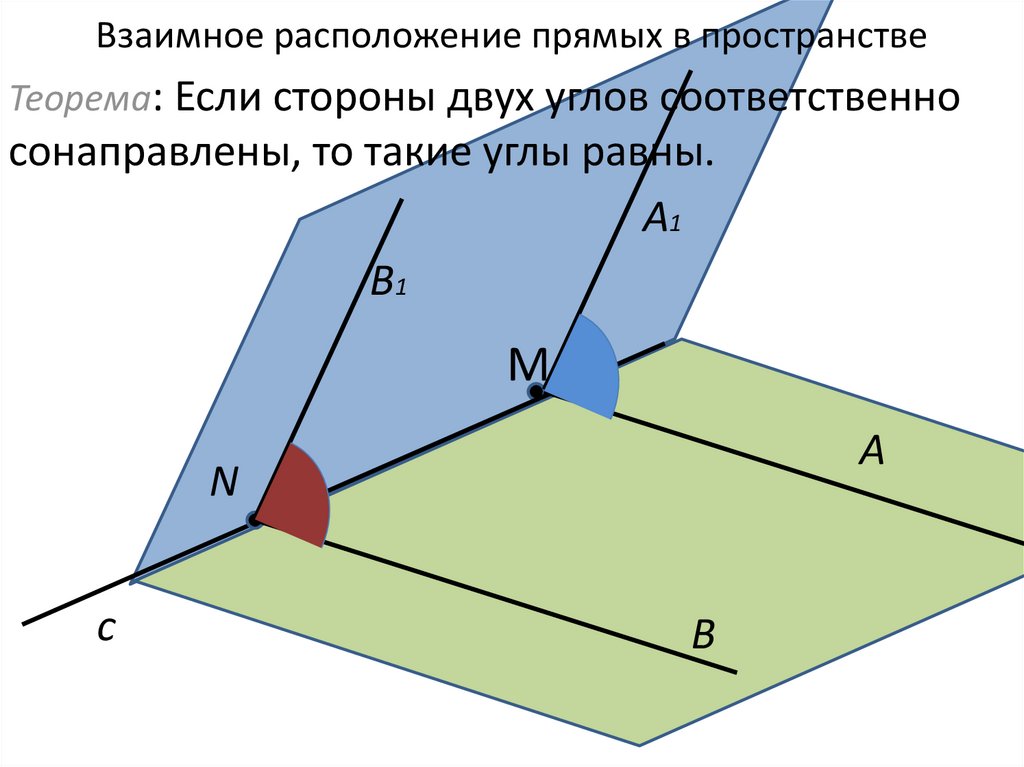
Теорема: Если стороны двух углов соответственносонаправлены, то такие углы равны.
А1
B1
M
A
N
c
B
35. Взаимное расположение прямых в пространстве
Теорема: Если стороны двух углов соответственносонаправлены, то такие углы равны.
А1
B1
M
A
N
c
B
36. Взаимное расположение прямых в пространстве
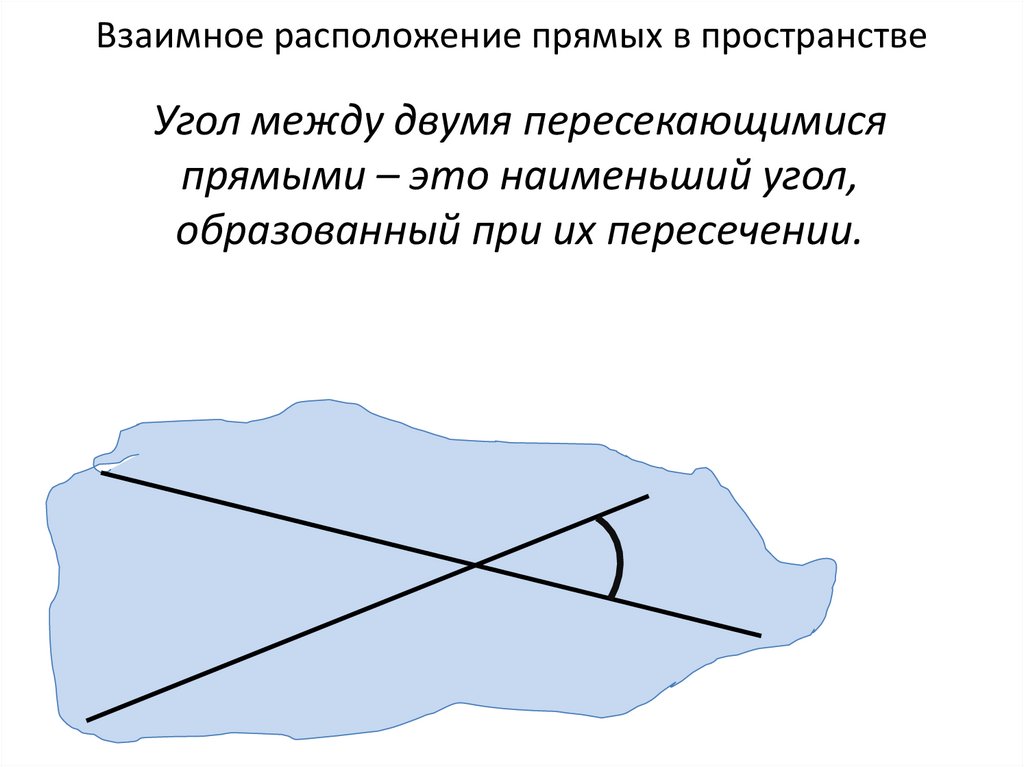
Угол между двумя пересекающимисяпрямыми – это наименьший угол,
образованный при их пересечении.
37. Взаимное расположение прямых в пространстве
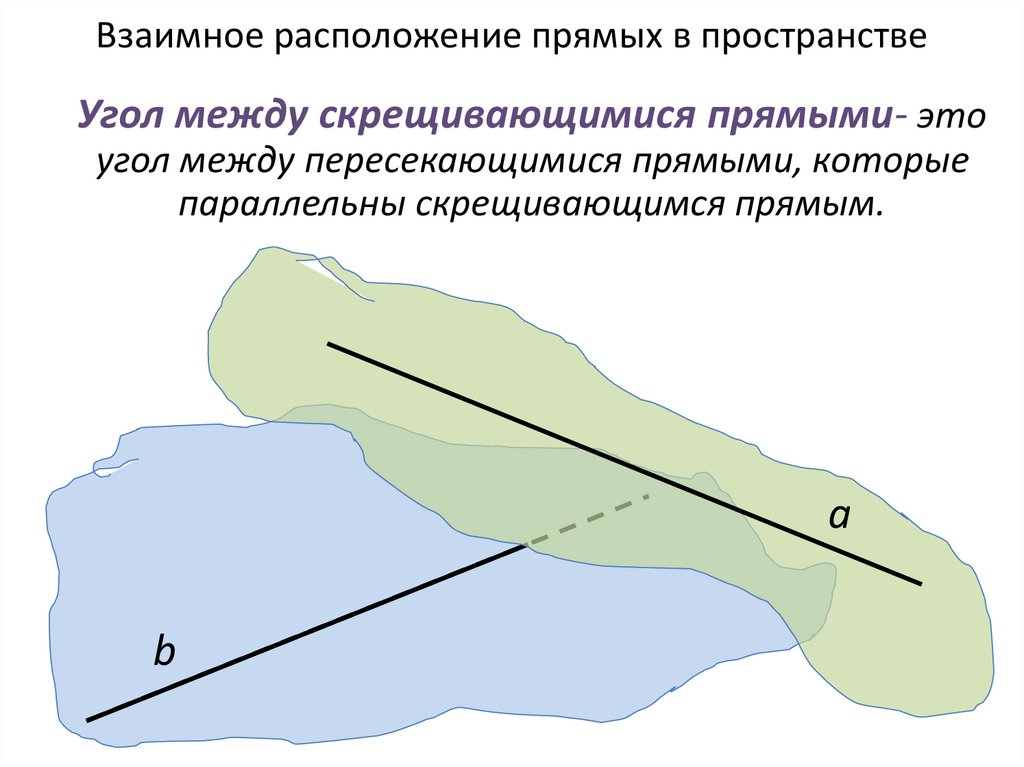
Угол между скрещивающимися прямыми- этоугол между пересекающимися прямыми, которые
параллельны скрещивающимся прямым.
a
b
38. Взаимное расположение прямых в пространстве
Угол между скрещивающимися прямыми- этоугол между пересекающимися прямыми, которые
параллельны скрещивающимся прямым.
a
φ
b
a1
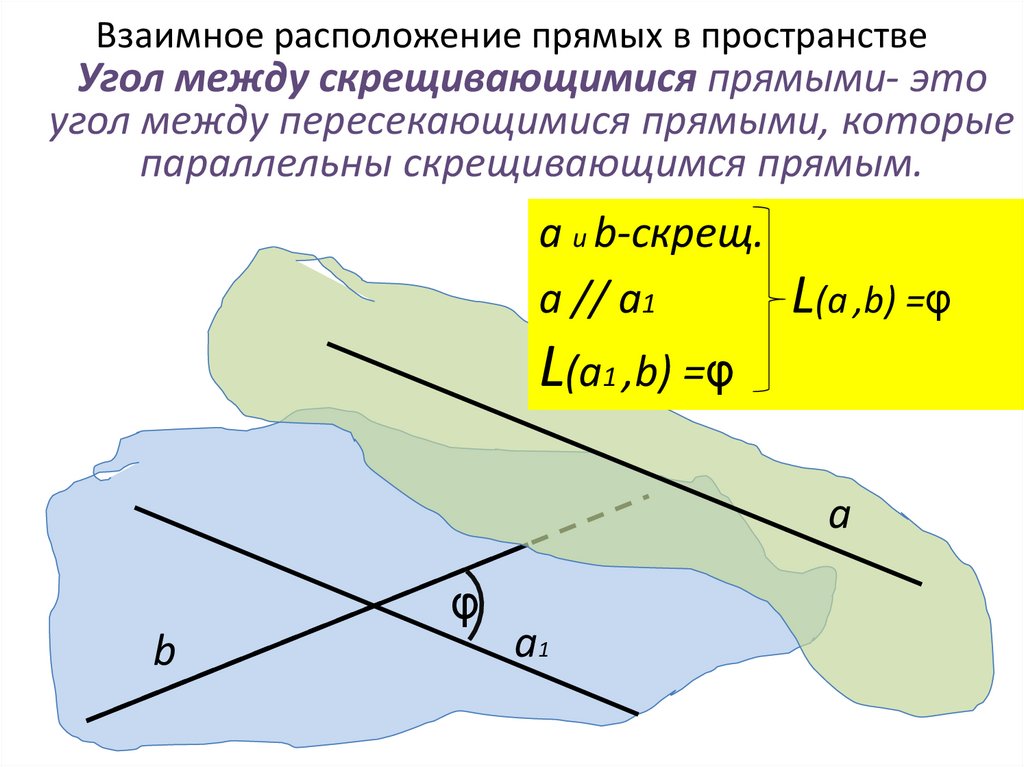
39. Взаимное расположение прямых в пространстве
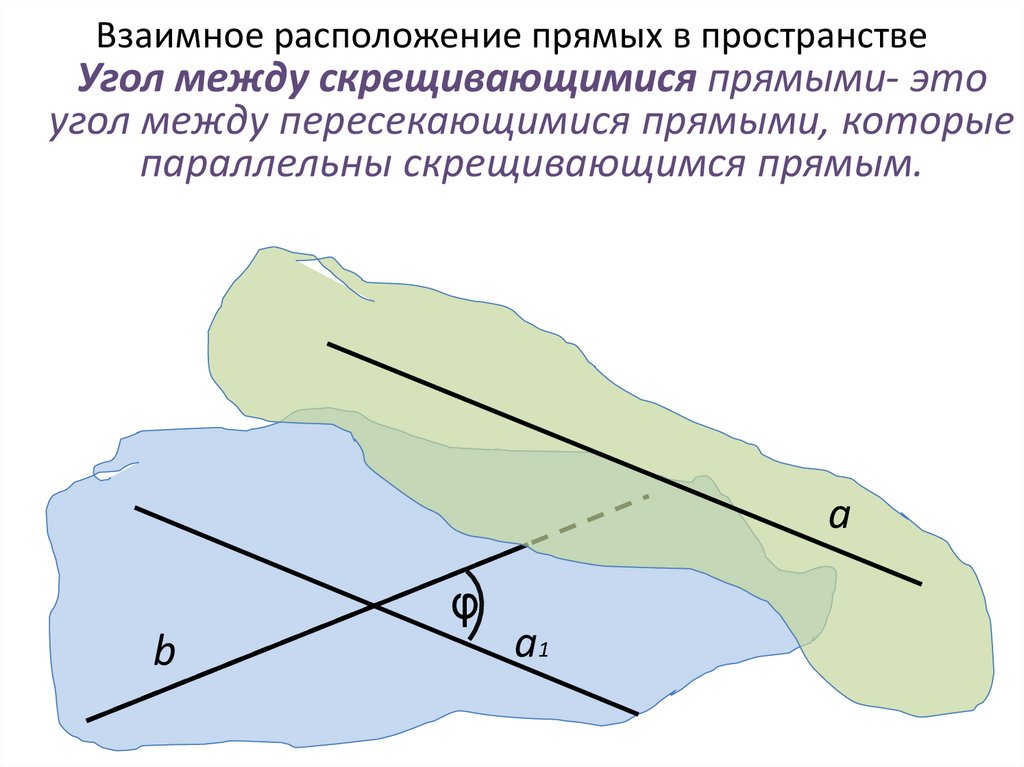
Угол между скрещивающимися прямыми- этоугол между пересекающимися прямыми, которые
параллельны скрещивающимся прямым.
а и b-скрещ.
а // a1
L(а ,b) =φ
L(а1 ,b) =φ
a
φ
b
a1
40.
Классная работа:Решаем задачи
№39,
№45
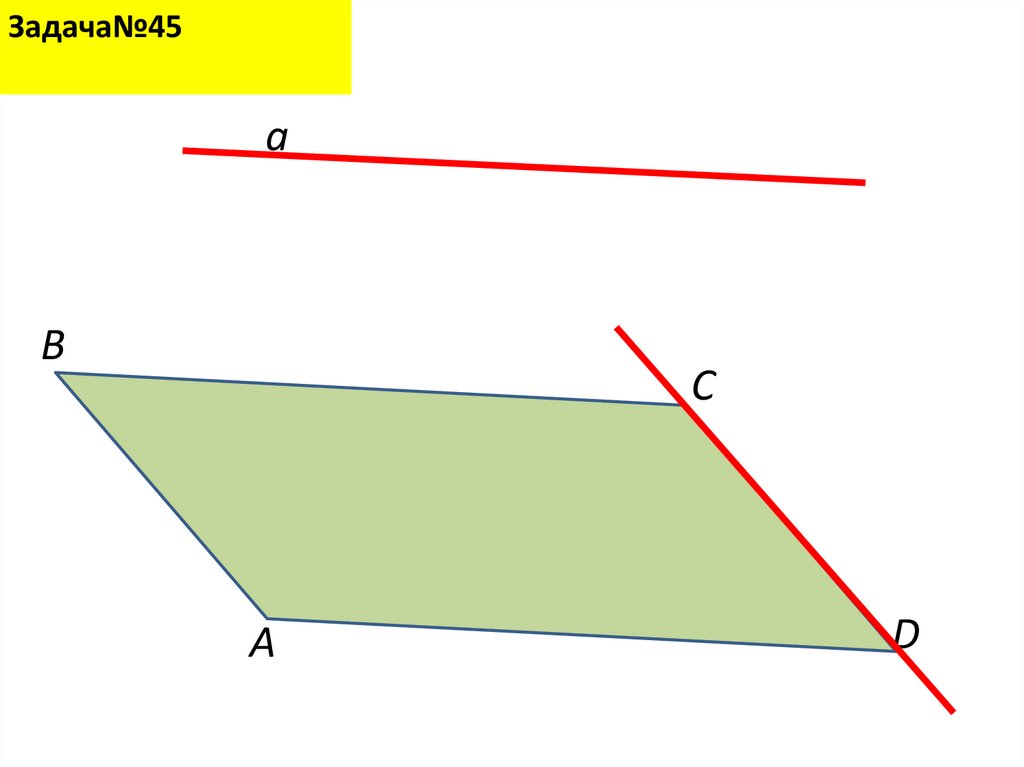
41.
Задача№45a
B
С
A
D
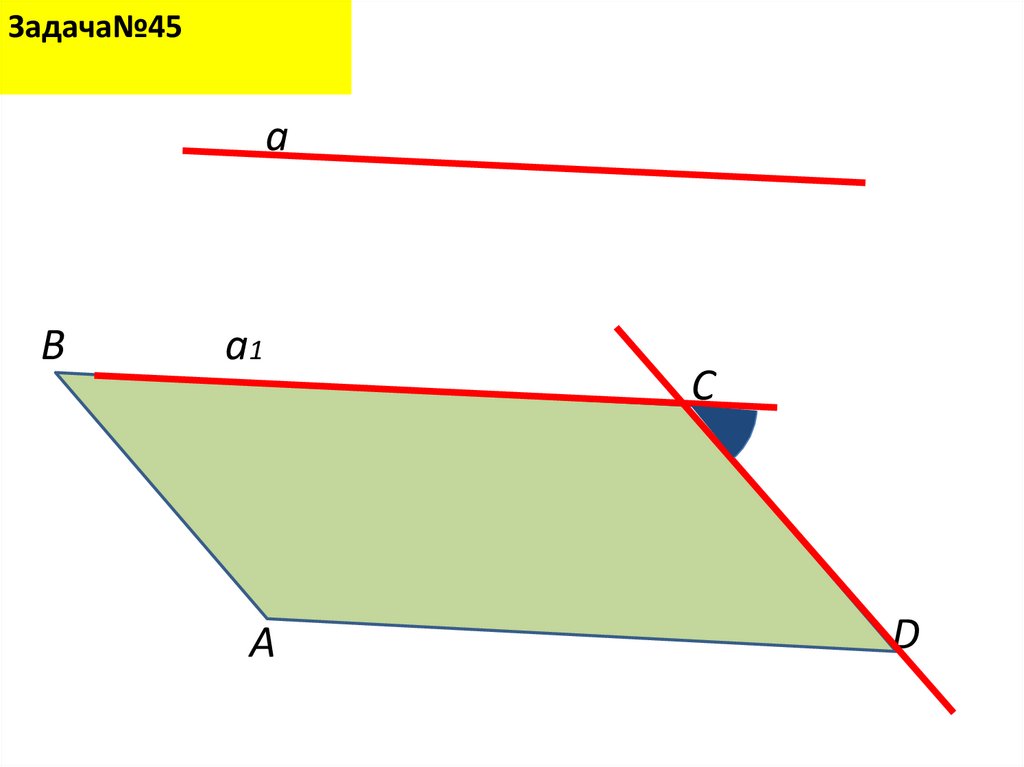
42.
Задача№45a
B
a1
A
С
D
43.
Домашнее задание:§2 п.7-9 читать, изучать,
выучить формулировки
теорем и определений;
Решать задачи № 35, 41, 44









 mathematics
mathematics